2021-2022学年七年级数学上册华东师大版5.2.3平行线的性质-同步练习(word解析版)
文档属性
| 名称 | 2021-2022学年七年级数学上册华东师大版5.2.3平行线的性质-同步练习(word解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 457.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 18:22:02 | ||
图片预览




文档简介
2021-2022学年七年级数学上册(华东师大版)
5.2.3平行线的性质(2)-同步练习
时间:60分钟
一、单选题
1.如图,,则满足的数量关系是(
)
A.
B.
C.
D.
2.如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的,第二次拐的,第三次拐的,这时的道路恰好和第一次拐弯之前的道路平行,则是(
)
A.
B.
C.
D.
3.如图所示,已知,,,的度数是(
)
A.
B.
C.
D.
4.如图,a∥b,若要使△ABC的面积与△DEF的面积相等,需增加条件(
)
A.AB=DE
B.AC=DF
C.BC=EF
D.BE=AD
5.如图,点P,M分别在直线AB和直线CD上,且AB∥CD,点P到CD的距离为5
cm,则点M到AB的距离( )
A.大于5
cm
B.小于5
cm
C.等于5
cm
D.不确定
6.如图,已知直线、被直线所截,,E是直线右边任意一点(点E不在直线,上),设,.下列各式:①,②,③,④,的度数可能是(
)
A.①②③
B.①②④
C.①③④
D.①②③④
7.两条平行线被第三条直线所截而成的角中,角平分线互相平行的是(
)
A.同位角和同旁内角
B.内错角和同旁内角
C.同位角和内错角
D.以上结论都不对
8.如图,a∥b,下列可以表示a,b之间的距离的是( )
A.线段AB的长度
B.线段AE的长度
C.线段EF的长度
D.线段BC的长度
二、填空题
9.如图,AB∥CD,AD不平行于BC,AC与BD相交于点O,写出三对面积相等的三角形是___________________.
10.如图所示,想在河堤两岸塔建一座桥,搭建方式最短的是_____,理由_____.
11.如图,直线分别与直线,相交于点,,平分,交直线于点,若,射线于点,则的度数为__度.
12.如图所示,一条公路两次转弯后又回到原来的方向(即),如果第一次转弯时;,那么应是_________.
13.如图,,则________.
14.在同一平面内,与直线AB的距离是3
cm的直线有________条.
15.如图,若,则____根据是__;若,则____,根据是__;若,则____,根据是__.
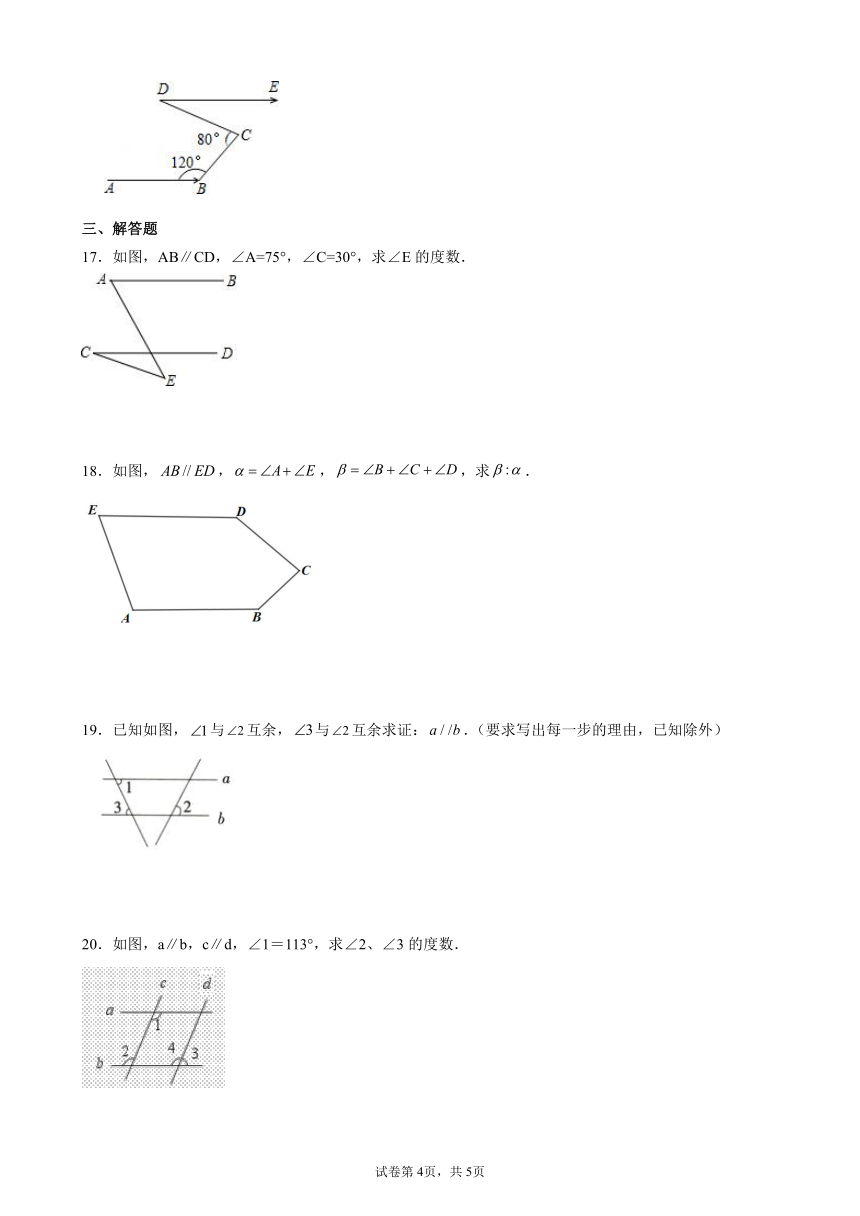
16.珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE=__________度.
三、解答题
17.如图,AB∥CD,∠A=75°,∠C=30°,求∠E的度数.
18.如图,,,,求.
19.已知如图,与互余,与互余求证:.(要求写出每一步的理由,已知除外)
20.如图,a∥b,c∥d,∠1=113°,求∠2、∠3的度数.
21.如图,在四边形ABCD,若AB∥CD,点P为BC上一点,设∠CDP=∠α,∠DPC=∠β,当点P在BC上运动时,∠α,∠β的和与∠B之间有何关系?请证明你的结论.
22.如图,在△ABC中,∠ABC与∠ACB的平分线相交于O.过点O作EF∥BC分别交AB、AC于E、F.若∠BOC=130°,∠ABC:∠ACB=3:2,求∠AEF和∠EFC.
23.如图,有一块地,PA、PB为水渠,水渠左边为张庄的地,右边为李庄的地.现要把水渠修直而不改变张庄、李庄原有的土地面积,如何修直?请用尺规作图简要说明.
24.如图,完成下列推理过程,已知AB∥CD,AC∥BD,
(1)∵AB∥CD(已知)
∴∠A=∠5(两直线平行,_______________);
(2)∵AC∥BD(已知) ∴∠3=∠4(两直线平行,_______________);
(3)∵AB∥CD(已知)
∴∠__=∠___(两直线平行,內錯角相等);
(4)∵AB∥CD(已知) ∴∠D
+∠______
=180°(两直线平行,____)
试卷第1页,共3页
参考答案
1.A
【解析】解:如图,过点C作CG∥AB,过点D作DH∥EF,
则∠A=∠ACG,∠EDH=180°-∠E,
∵AB∥EF,
∴CG∥DH,
∴∠CDH=∠DCG,
∴∠ACD=∠ACG+∠CDH=∠A+∠CDE-(180°-∠E),
∴∠A-∠ACD
+∠CDE
+∠E=180°.
即
故选:A.
2.D
【解析】解:过点B作直线BD与第一次拐弯的道路平行,如图所示:
∵第三次拐的,这时的道路恰好和第一次拐弯之前的道路平行,
∴直线BD与第三次拐弯的道路也平行,
∵,
∴,,
∵,
∴,
∴;
故选D.
3.A
【解析】过点B作BM∥AC,
∵,
∴,
∴,,
∵,
∴,
∴.
故选:A.
4.C
【解析】两条平行线之间的距离处处相等,则△ABC和△DEF的高相等,则要使面积相等必须满足底相等,故本题选C.
5.C
【解析】解:∵AB∥CD,
点P到CD的距离为5
cm,
∴点M到AB的距离等于5
cm,
故选C.
6.A
【解析】解:(1)如图,由AB∥CD,可得∠AOC=∠DCE1=β,
∵∠AOC=∠BAE1+∠AE1C,
∴∠AE1C=β-α.
(2)如图,过E2作AB平行线,则由AB∥CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,
∴∠AE2C=α+β.
(3)当点E在CD的下方时,同理可得,∠AEC=α-β.
综上所述,∠AEC的度数可能为β-α,α+β,α-β.
即①α+β,②α-β,③β-α,都成立.
故选A.
7.C
【解析】如图所示:
可得角平分线互相平行的是同位角和内错角.
故选:.
8.C
【解析】由直线a∥b,EF⊥b,得线段EF的长度是直线a,b之间距离,
故选:C.
9.△ADC和△BDC;△ADO和△BCO;△DAB和△CAB
【解析】根据AB∥CD可得:△ABC和△ABD的面积相等,△ACD和△BCD的面积相等,则△ACD的面积减去△OCD的面积等于△BCD的面积减去△OCD的面积,即△AOD和△BOC的面积相等.
10.PN,
垂线段最短
【解析】∵PM⊥MN,
∴由垂线段最短可知PM是最短的,
故答案为PM,垂线段最短.
11.59或121
【解析】解:如图,①当射线于点时,,
,
,
,
平分,
,
,
;
②当射线于点时,,
同理:.
则的度数为59或121度.
答案:59或121.
12.140
【解析】解:∵(已知)
∴∠C=∠B=140°(两直线平行,内错角相等)
故答案为:140.
13.4∶3
【解析】解:如图所示:过点作.
,
.
,,
,
.
.
同理:.
∵,
∴
.
.
故答案为:.
14.2
【解析】解:与直线AB的距离是3
cm的直线有2条,
这两条直线位于AB的异侧.
15.
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
【解析】若,则根据是同位角相等,两直线平行;
若,则,根据是内错角相等,两直线平行;
若,则,根据是同旁内角互补,两直线平行.
故答案为:,,同位角相等,两直线平行;,,内错角相等,两直线平行;,,同旁内角互补,两直线平行.
16.20
【解析】解:过点C作CF∥AB,
已知珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,
∴AB∥DE,
∴CF∥DE,
∴∠BCF+∠ABC=180°,
∴∠BCF=60°,
∴∠DCF=20°,
∴∠CDE=∠DCF=20°.
故答案为20.
17.45°.
【解析】解:∵AB∥CD,∠A=75°,
∴∠1=∠A=75°,
∵∠C=30°,
∴∠E=∠1﹣∠C=75°﹣30°=45°.
18.2:1
【解析】解:过C点作CF∥AB,
∵AB∥ED,
∴CF∥DE,
∴∠B+∠2=∠D+∠1=180°,
∴β=∠B+∠BCD+∠D=∠B+∠2+∠D+∠1=360°,
∵AB∥DE,
∴∠A+∠E=α=180°,
∴β:α=360°:180°=2:1,
19.见解析
【解析】∵与互余,与互余
∴(同角的余角相等)
∴(内错角相等,两直线平行).
20.∠2=113°,∠3=67°.
【解析】∵a∥b,
∴∠1=∠2,
∵∠1=113°,
∴∠2=113°,
∵c∥d,
∴∠2=∠4=113°,
∴∠3=180°-113°=67°.
21.
【解析】∠α+∠β=∠B.证明如下:
过点P作PQ∥CD交AD于点Q,则∠DPQ=∠α(两直线平行,内错角相等).
∵AB∥CD(已知),∴PQ∥AB(平行公理的推论),∴∠B=∠CPQ(两直线平行,同位角相等).
又∵∠CPQ=∠DPQ+∠β,∴∠α+∠β=∠B(等量代换).
22.∠AEF=60°,∠EFC=140°.
【解析】∵∠ABC:
∠ACB=3:2,
∴设∠ABC=3x,
∠ACB=2x,
∵BO、CO分别平分
∠
ABC、
∠
ACB,
∴∠ABO=∠CBO=x,∠ACO=∠BCO=x,
又∵∠BOC=130°,
在△BOC中,∠BOC+∠OBC+∠OCB=180°,
∴130°+x+x=180°,
解得:x=20°,
∴∠ABC=3x=60°,
∠ACB=2x=40°,
∵EF∥BC,
∴∠AEF=∠ABC=60°,
∠EFC+∠ACB=180°,
∴∠EFC=140°.
23.作图见解析.
【解析】
如图,由平行线之间的距离相等可以得出△ABG与△ABP的面积相等,此时,张庄与李庄的面积与原来保持不变.
24.同位角相等,內錯角相等,1,2,ABD,同旁内角互补.
【解析】(1)∵AB∥CD(已知)
∴∠A=∠5(两直线平行,同位角相等);
(2)∵AC∥BD(已知) ∴∠3=∠4(两直线平行,內錯角相等);
(3)∵AB∥CD(已知)
∴∠1=∠2(两直线平行,內錯角相等);
(4)∵AB∥CD(已知) ∴∠D
+∠ABD
=180°(两直线平行,同旁内角互补)
答案第1页,共2页
答案第1页,共2页
5.2.3平行线的性质(2)-同步练习
时间:60分钟
一、单选题
1.如图,,则满足的数量关系是(
)
A.
B.
C.
D.
2.如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的,第二次拐的,第三次拐的,这时的道路恰好和第一次拐弯之前的道路平行,则是(
)
A.
B.
C.
D.
3.如图所示,已知,,,的度数是(
)
A.
B.
C.
D.
4.如图,a∥b,若要使△ABC的面积与△DEF的面积相等,需增加条件(
)
A.AB=DE
B.AC=DF
C.BC=EF
D.BE=AD
5.如图,点P,M分别在直线AB和直线CD上,且AB∥CD,点P到CD的距离为5
cm,则点M到AB的距离( )
A.大于5
cm
B.小于5
cm
C.等于5
cm
D.不确定
6.如图,已知直线、被直线所截,,E是直线右边任意一点(点E不在直线,上),设,.下列各式:①,②,③,④,的度数可能是(
)
A.①②③
B.①②④
C.①③④
D.①②③④
7.两条平行线被第三条直线所截而成的角中,角平分线互相平行的是(
)
A.同位角和同旁内角
B.内错角和同旁内角
C.同位角和内错角
D.以上结论都不对
8.如图,a∥b,下列可以表示a,b之间的距离的是( )
A.线段AB的长度
B.线段AE的长度
C.线段EF的长度
D.线段BC的长度
二、填空题
9.如图,AB∥CD,AD不平行于BC,AC与BD相交于点O,写出三对面积相等的三角形是___________________.
10.如图所示,想在河堤两岸塔建一座桥,搭建方式最短的是_____,理由_____.
11.如图,直线分别与直线,相交于点,,平分,交直线于点,若,射线于点,则的度数为__度.
12.如图所示,一条公路两次转弯后又回到原来的方向(即),如果第一次转弯时;,那么应是_________.
13.如图,,则________.
14.在同一平面内,与直线AB的距离是3
cm的直线有________条.
15.如图,若,则____根据是__;若,则____,根据是__;若,则____,根据是__.
16.珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE=__________度.
三、解答题
17.如图,AB∥CD,∠A=75°,∠C=30°,求∠E的度数.
18.如图,,,,求.
19.已知如图,与互余,与互余求证:.(要求写出每一步的理由,已知除外)
20.如图,a∥b,c∥d,∠1=113°,求∠2、∠3的度数.
21.如图,在四边形ABCD,若AB∥CD,点P为BC上一点,设∠CDP=∠α,∠DPC=∠β,当点P在BC上运动时,∠α,∠β的和与∠B之间有何关系?请证明你的结论.
22.如图,在△ABC中,∠ABC与∠ACB的平分线相交于O.过点O作EF∥BC分别交AB、AC于E、F.若∠BOC=130°,∠ABC:∠ACB=3:2,求∠AEF和∠EFC.
23.如图,有一块地,PA、PB为水渠,水渠左边为张庄的地,右边为李庄的地.现要把水渠修直而不改变张庄、李庄原有的土地面积,如何修直?请用尺规作图简要说明.
24.如图,完成下列推理过程,已知AB∥CD,AC∥BD,
(1)∵AB∥CD(已知)
∴∠A=∠5(两直线平行,_______________);
(2)∵AC∥BD(已知) ∴∠3=∠4(两直线平行,_______________);
(3)∵AB∥CD(已知)
∴∠__=∠___(两直线平行,內錯角相等);
(4)∵AB∥CD(已知) ∴∠D
+∠______
=180°(两直线平行,____)
试卷第1页,共3页
参考答案
1.A
【解析】解:如图,过点C作CG∥AB,过点D作DH∥EF,
则∠A=∠ACG,∠EDH=180°-∠E,
∵AB∥EF,
∴CG∥DH,
∴∠CDH=∠DCG,
∴∠ACD=∠ACG+∠CDH=∠A+∠CDE-(180°-∠E),
∴∠A-∠ACD
+∠CDE
+∠E=180°.
即
故选:A.
2.D
【解析】解:过点B作直线BD与第一次拐弯的道路平行,如图所示:
∵第三次拐的,这时的道路恰好和第一次拐弯之前的道路平行,
∴直线BD与第三次拐弯的道路也平行,
∵,
∴,,
∵,
∴,
∴;
故选D.
3.A
【解析】过点B作BM∥AC,
∵,
∴,
∴,,
∵,
∴,
∴.
故选:A.
4.C
【解析】两条平行线之间的距离处处相等,则△ABC和△DEF的高相等,则要使面积相等必须满足底相等,故本题选C.
5.C
【解析】解:∵AB∥CD,
点P到CD的距离为5
cm,
∴点M到AB的距离等于5
cm,
故选C.
6.A
【解析】解:(1)如图,由AB∥CD,可得∠AOC=∠DCE1=β,
∵∠AOC=∠BAE1+∠AE1C,
∴∠AE1C=β-α.
(2)如图,过E2作AB平行线,则由AB∥CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,
∴∠AE2C=α+β.
(3)当点E在CD的下方时,同理可得,∠AEC=α-β.
综上所述,∠AEC的度数可能为β-α,α+β,α-β.
即①α+β,②α-β,③β-α,都成立.
故选A.
7.C
【解析】如图所示:
可得角平分线互相平行的是同位角和内错角.
故选:.
8.C
【解析】由直线a∥b,EF⊥b,得线段EF的长度是直线a,b之间距离,
故选:C.
9.△ADC和△BDC;△ADO和△BCO;△DAB和△CAB
【解析】根据AB∥CD可得:△ABC和△ABD的面积相等,△ACD和△BCD的面积相等,则△ACD的面积减去△OCD的面积等于△BCD的面积减去△OCD的面积,即△AOD和△BOC的面积相等.
10.PN,
垂线段最短
【解析】∵PM⊥MN,
∴由垂线段最短可知PM是最短的,
故答案为PM,垂线段最短.
11.59或121
【解析】解:如图,①当射线于点时,,
,
,
,
平分,
,
,
;
②当射线于点时,,
同理:.
则的度数为59或121度.
答案:59或121.
12.140
【解析】解:∵(已知)
∴∠C=∠B=140°(两直线平行,内错角相等)
故答案为:140.
13.4∶3
【解析】解:如图所示:过点作.
,
.
,,
,
.
.
同理:.
∵,
∴
.
.
故答案为:.
14.2
【解析】解:与直线AB的距离是3
cm的直线有2条,
这两条直线位于AB的异侧.
15.
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
【解析】若,则根据是同位角相等,两直线平行;
若,则,根据是内错角相等,两直线平行;
若,则,根据是同旁内角互补,两直线平行.
故答案为:,,同位角相等,两直线平行;,,内错角相等,两直线平行;,,同旁内角互补,两直线平行.
16.20
【解析】解:过点C作CF∥AB,
已知珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,
∴AB∥DE,
∴CF∥DE,
∴∠BCF+∠ABC=180°,
∴∠BCF=60°,
∴∠DCF=20°,
∴∠CDE=∠DCF=20°.
故答案为20.
17.45°.
【解析】解:∵AB∥CD,∠A=75°,
∴∠1=∠A=75°,
∵∠C=30°,
∴∠E=∠1﹣∠C=75°﹣30°=45°.
18.2:1
【解析】解:过C点作CF∥AB,
∵AB∥ED,
∴CF∥DE,
∴∠B+∠2=∠D+∠1=180°,
∴β=∠B+∠BCD+∠D=∠B+∠2+∠D+∠1=360°,
∵AB∥DE,
∴∠A+∠E=α=180°,
∴β:α=360°:180°=2:1,
19.见解析
【解析】∵与互余,与互余
∴(同角的余角相等)
∴(内错角相等,两直线平行).
20.∠2=113°,∠3=67°.
【解析】∵a∥b,
∴∠1=∠2,
∵∠1=113°,
∴∠2=113°,
∵c∥d,
∴∠2=∠4=113°,
∴∠3=180°-113°=67°.
21.
【解析】∠α+∠β=∠B.证明如下:
过点P作PQ∥CD交AD于点Q,则∠DPQ=∠α(两直线平行,内错角相等).
∵AB∥CD(已知),∴PQ∥AB(平行公理的推论),∴∠B=∠CPQ(两直线平行,同位角相等).
又∵∠CPQ=∠DPQ+∠β,∴∠α+∠β=∠B(等量代换).
22.∠AEF=60°,∠EFC=140°.
【解析】∵∠ABC:
∠ACB=3:2,
∴设∠ABC=3x,
∠ACB=2x,
∵BO、CO分别平分
∠
ABC、
∠
ACB,
∴∠ABO=∠CBO=x,∠ACO=∠BCO=x,
又∵∠BOC=130°,
在△BOC中,∠BOC+∠OBC+∠OCB=180°,
∴130°+x+x=180°,
解得:x=20°,
∴∠ABC=3x=60°,
∠ACB=2x=40°,
∵EF∥BC,
∴∠AEF=∠ABC=60°,
∠EFC+∠ACB=180°,
∴∠EFC=140°.
23.作图见解析.
【解析】
如图,由平行线之间的距离相等可以得出△ABG与△ABP的面积相等,此时,张庄与李庄的面积与原来保持不变.
24.同位角相等,內錯角相等,1,2,ABD,同旁内角互补.
【解析】(1)∵AB∥CD(已知)
∴∠A=∠5(两直线平行,同位角相等);
(2)∵AC∥BD(已知) ∴∠3=∠4(两直线平行,內錯角相等);
(3)∵AB∥CD(已知)
∴∠1=∠2(两直线平行,內錯角相等);
(4)∵AB∥CD(已知) ∴∠D
+∠ABD
=180°(两直线平行,同旁内角互补)
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
