2021-2022学年华东师大版八年级数学上册13.5.2线段垂直平分线同步练习 (Word版,含答案)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学上册13.5.2线段垂直平分线同步练习 (Word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 579.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 22:49:13 | ||
图片预览


文档简介
2021-2022学年八年级数学上册(华东师大版)
13.5.2线段垂直平分线-同步练习
时间:60分钟
一、单选题
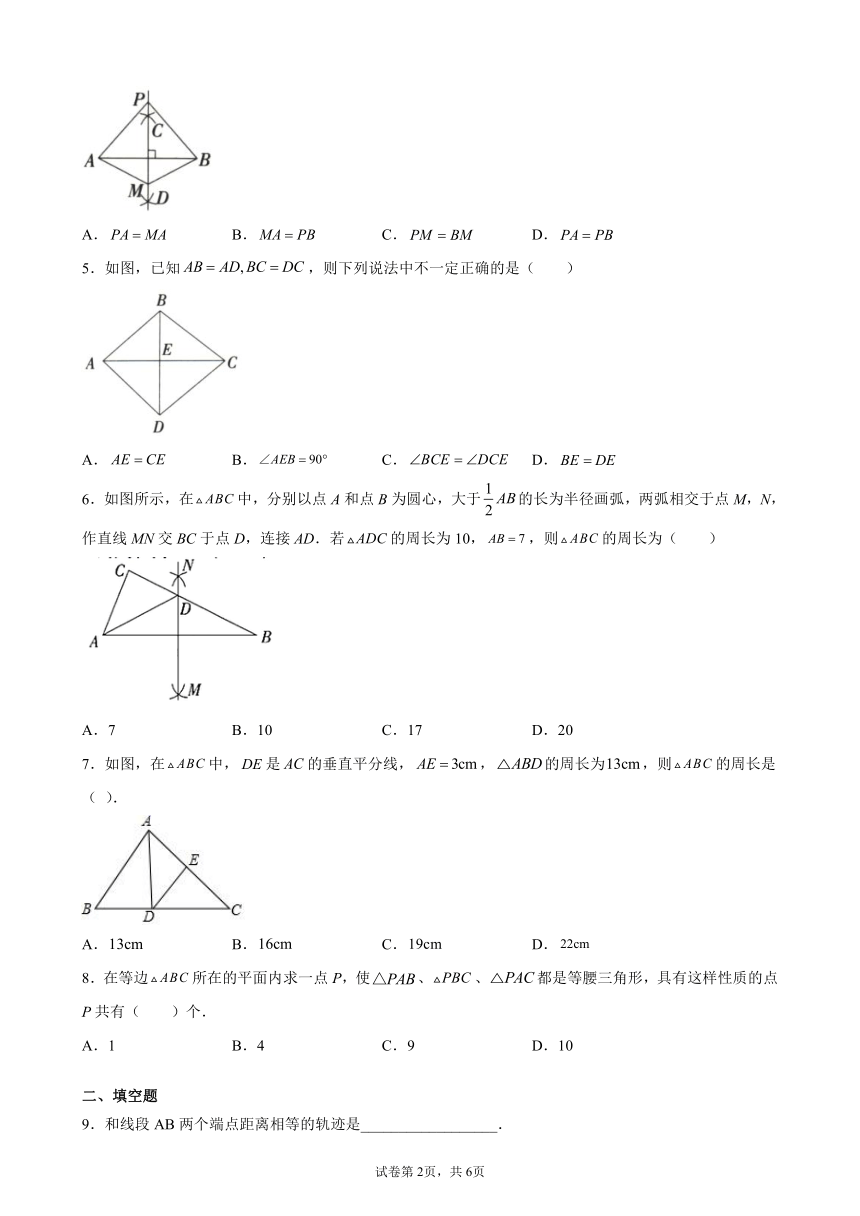
1.如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
2.如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在(
).
A.在
AC、BC
两边高线的交点处
B.在
AC、BC
两边垂直平分线的交点处
C.在
AC、BC
两边中线的交点处
D.在∠A、∠B两内角平分线的交点处
3.如图,直线与交于点O,,下列结论中正确的是(
)
A.
B.
C.是的垂直平分线
D.点P在的垂直平分线上
4.如图,已知线段,分别以点A、B为圆心,大于的长为半径画弧,两弧交于点C和点D,作直线,在上取两点P、M,连接、、、,则下列结论一定正确的是(
)
A.
B.
C.
D.
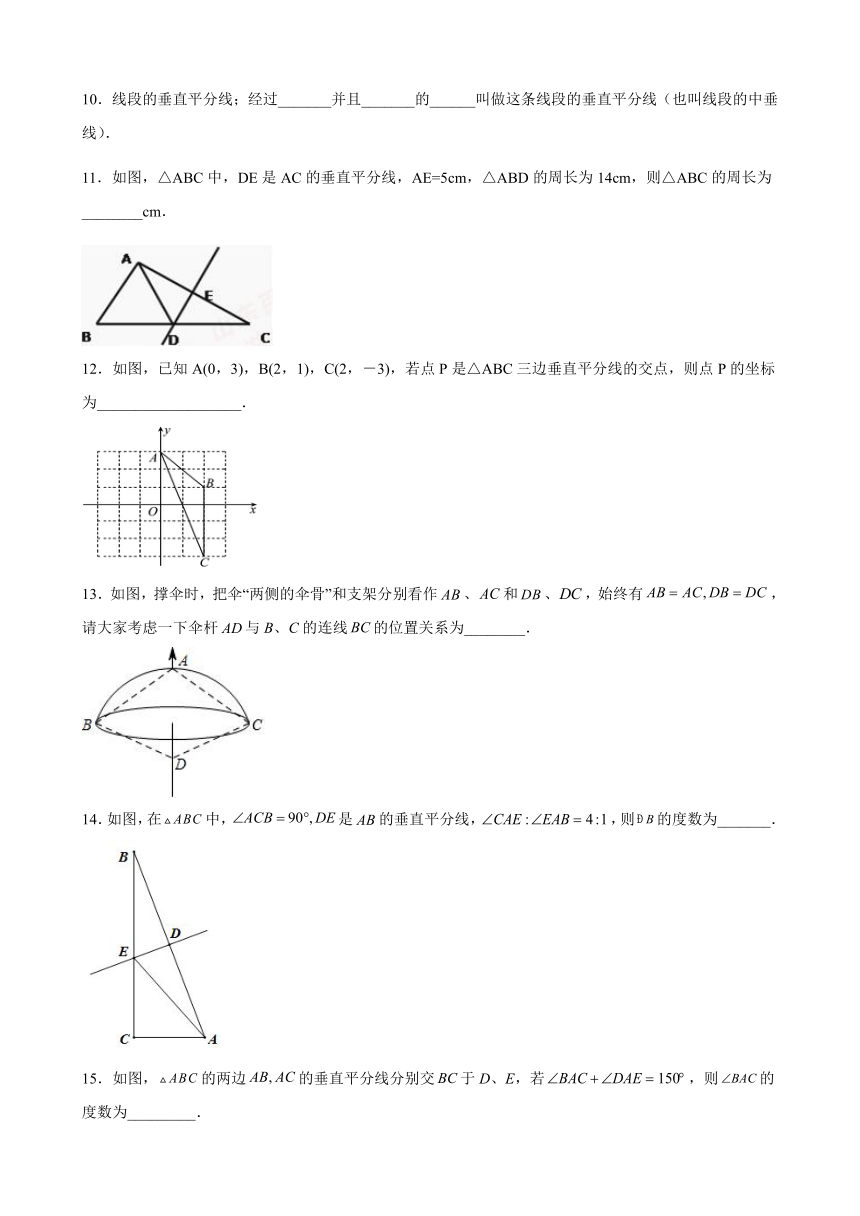
5.如图,已知,则下列说法中不一定正确的是(
)
A.
B.
C.
D.
6.如图所示,在中,分别以点A和点B为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD.若的周长为10,,则的周长为(
)
A.7
B.10
C.17
D.20
7.如图,在中,是的垂直平分线,,的周长为,则的周长是(
).
A.
B.
C.
D.
8.在等边所在的平面内求一点P,使、、都是等腰三角形,具有这样性质的点P共有(
)个.
A.1
B.4
C.9
D.10
二、填空题
9.和线段AB两个端点距离相等的轨迹是__________________.
10.线段的垂直平分线;经过_______并且_______的______叫做这条线段的垂直平分线(也叫线段的中垂线).
11.如图,△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为14cm,则△ABC的周长为________cm.
12.如图,已知A(0,3),B(2,1),C(2,-3),若点P是△ABC三边垂直平分线的交点,则点P的坐标为___________________.
13.如图,撑伞时,把伞“两侧的伞骨”和支架分别看作、和、,始终有,请大家考虑一下伞杆与B、C的连线的位置关系为________.
14.如图,在中,是的垂直平分线,,则的度数为_______.
15.如图,的两边的垂直平分线分别交于D、E,若,则的度数为_________.
16.△ABC中,若AB﹣AC=2cm,BC的垂直平分线交AB于D点,且△ACD的周长为14cm,则AB=_____,AC=_____.
三、解答题
17.直角三角形的一个锐角为,请将它分成三部分,要求每一部分的大小、形状都相同,画出图形.
18.如图,直线1外有两点A、B,请在直线l上找一点P,使得点P到点A和点B的距离相等.(尺规作图,不写作法,写清结论)
19.证明定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.已知:如图,A为线段外任意一点,且.求证:点A在的垂直平分线上.
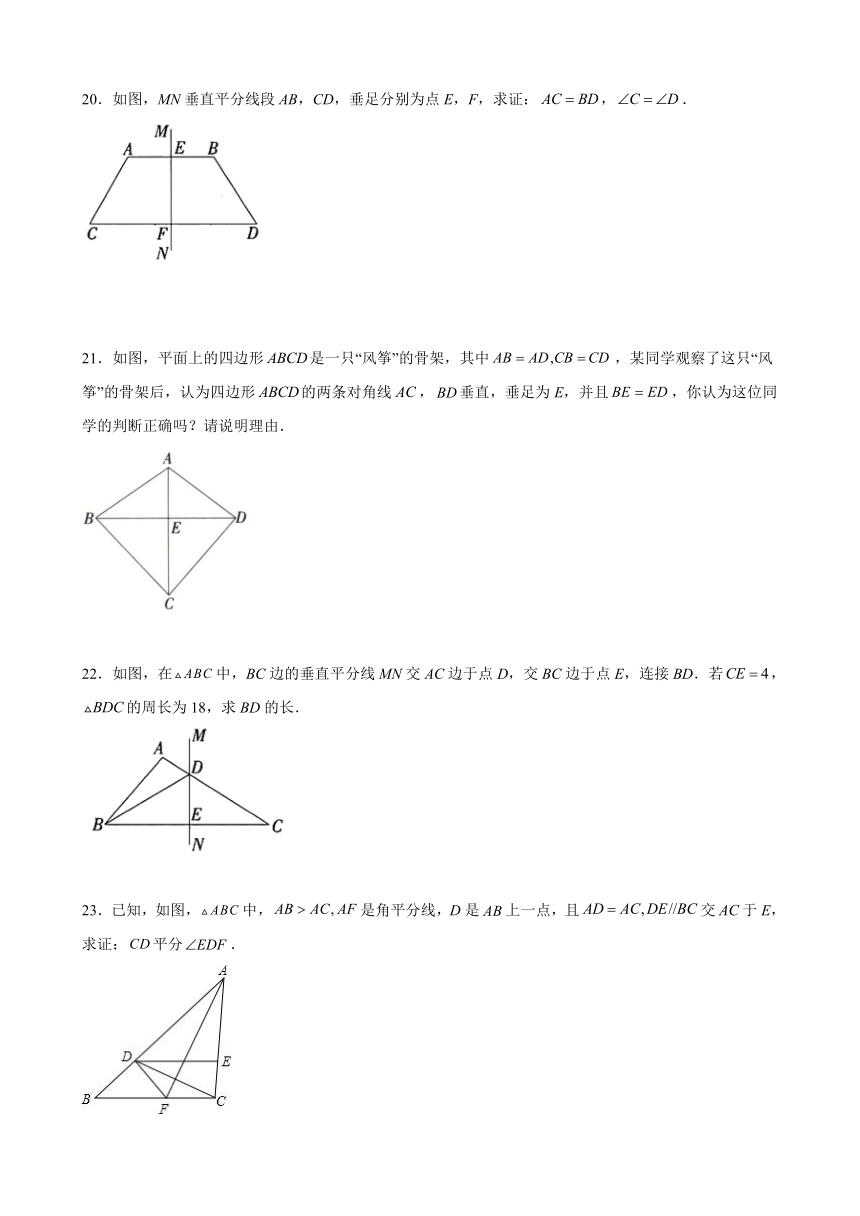
20.如图,MN垂直平分线段AB,CD,垂足分别为点E,F,求证:,.
21.如图,平面上的四边形是一只“风筝”的骨架,其中,某同学观察了这只“风筝”的骨架后,认为四边形的两条对角线,垂直,垂足为E,并且,你认为这位同学的判断正确吗?请说明理由.
22.如图,在中,BC边的垂直平分线MN交AC边于点D,交BC边于点E,连接BD.若,的周长为18,求BD的长.
23.已知,如图,中,是角平分线,D是上一点,且交于E,求证:平分.
24.如图,小河边有两个村庄A、B.要在河边建一自来水厂向A村与B村供水.
(1)若要使水厂到A、B村的距离相等,则应选择在哪建厂?
(2)若要使水厂到A、B村的水管最省料,应建在什么地方?(保留作图痕迹,不写作法)
25.如图,在中,,AB的垂直平分线DE交AC于D,垂足为E,若,.
求的度数;
求AC的长度.
试卷第1页,共3页
参考答案
1.A
【解析】∵AC=AD,BC=BD,
∴点A在CD的垂直平分线上,点B在CD的垂直平分线上,
∴AB是CD的垂直平分线.
即AB垂直平分CD.
故选A
2.B
【解析】解:根据线段垂直平分线上的点到线段两个端点的距离相等,
可知超市应建在AC、BC两边垂直平分线的交点处,
故选:B.
3.D
【解析】解:因为直线PO与AB交于点O,且PA=PB,
所以P在线段AB的垂直平分线上,
故选:D.
4.D
【解析】解:由题意可知,直线是线段的垂直平分线,所以.
故选择:D
5.A
【解析】解:∵,
∴垂直平分线段,
∴,,,
故正确,不符合题意;
∴只有选项A不一定正确,符合题意.
故选:
6.C
【解析】首先根据题意可得MN是线段AB的垂直平分线,即可得,又由的周长为10,求得,则可求得的周长为.
答案:C
7.C
【解析】解:∵DE是AC的垂直平分线,
∴AD=CD,AC=2AE=6cm,
又∵△ABD的周长=AB+BD+AD=13cm,
∴AB+BD+CD=13cm,
即AB+BC=13cm,
∴△ABC的周长=AB+BC+AC=13+6=19cm.
故选C.
8.D
【解析】①当点P在三角形的内部时,点P是边AB、BC、AC的垂直平分线的交点,是三角形的外心,如图点.
②当P在三角形的外部时,分别以三角形各顶点为圆心,边长为半径画弧,与垂直平分线的交点有3个,如图,点,共9个.
综上具有这样性质的点P共有10个.
故选:D.
9.线段AB的垂直平分线
【解析】到线段AB两个端点的距离相等的点的轨迹是线段AB的垂直平分线,
故答案为:线段AB的垂直平分线.
10.线段的中点
垂直于这条线段
直线
【解析】解:经过线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
故填:线段的中点,垂直于这条线段,直线.
11.24
【解析】∵DE是AC的垂直平分线
∴AD=CD,AE=EC=5cm,
∴AC=10cm
∵△ABD的周长为14cm
∴AB+BD+AD=14,
△ABC的周长为AB+BC+AC=
AB+
BD+
CD+AC=
AB+BD+AD+AC=14+10=24cm.
12.(-2,-1)
【解析】设p点坐标为(a,b),则有
,
解得:a=
-2,b=-1,
所以P点的坐标为(-2,-1).
故答案为(-2,-1)
13.垂直
【解析】解:如图,连接、,
∵,
∴点A在线段的垂直平分线上,点D在线段的垂直平分线上,
∴根据两点确定一条直线得出直线是线段的垂直平分线,
故答案为:垂直.
14.15°
【解析】解:∵在Rt△ABC中,,
∵DE是AB的垂直平分线
∴∠B=∠BAE
∵∠CAE:∠EAB=4:1
∴6∠B=90°
∴∠B=15°
故答案为:15°.
15.
【解析】解:∵△ABC的两边AB,AC的垂直平分线分别交BC于D,E,
∴DA=DB,EA=EC,
∴∠B=∠DAB,∠C=∠EAC.
∵∠BAC+∠DAE=150°,①
∴∠B+∠C+2∠DAE=150°.
∵∠B+∠C+∠BAC=180°,
∴180°-∠BAC+2∠DAE=150°,
即∠BAC-2∠DAE=30°.②
由①②组成的方程组,
解得∠BAC=110°.
故答案为:110°.
16.AB=8cm
AC=6cm
【解析】根据线段垂直平分线性质求出BD=DC,根据三角形周长AD+BD+AC=AB+AC=14cm,根据已知得出AC=AB-2cm,即可求出AC=6cm,AB=8cm.
故答案为8,6.
17.作图见解析,理由见解析
【解析】解:如图,△ACE,△AEF,△EFB即为所求.
理由如下:
由作图可得:是AB的垂直平分线,
所以每一部分的大小、形状都相同,
18.见解析.
【解析】解:作AB的垂直平分线CD,交直线l于P,
点P为所求
19.见解析
【解析】证明:如图,作于点D,
∵,
∴,
在和中,
∴.
∴,
∴直线是线段的垂直平分线,
∴点A在的垂直平分线上.
20.见解析
【解析】答案:证明:如图,连接EC、ED,
∵MN垂直平分线段AB,∴,,又∵MN垂直平分线段CD,∴,由对称性得,,∴,即,在和中,
∴(SAS),
∴,,
又,∴,即.
易错:证明:∵MN垂直平分线段AB,∴,
∵MN垂直平分线段CD,∴,
∴,.
21.正确,理由见解析
【解析】解:正确理由如下:
∵,
∴点A在的垂直平分线上.
又∵,
∴点C在的垂直平分线上.
∴所在直线为的垂直平分线,
∴.
22.5
【解析】解析:根据线段垂直平分线的性质得到,,根据三角形的周长公式计算即可.
答案:解:∵MN垂直平分BC,∴,,又∵,,又∵的周长为18,∴.∴.
23.见解析
【解析】证明:∵AD=AC,是角平分线,
∴AF垂直平分CD,
∴CF=DF,
∴∠FDC=∠FCD,
∵,
∴∠EDC=∠DCF,
∴∠EDC=FDC,
∴CD平分∠EDF.
24.(1)答案见解析;(2)答案见解析.
【解析】解:(1)作出AB的中垂线与EF的交点M,交点M即为厂址所在位置;
(2)如图所示:作A点关于直线EF的对称点A′,再连接A′B交EF于点N,点N即为所求.
25.(1)(2)6
【解析】垂直平分AB,
,
,
;
,,
,
,
.
.
答案第1页,共2页
答案第1页,共2页
13.5.2线段垂直平分线-同步练习
时间:60分钟
一、单选题
1.如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
2.如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在(
).
A.在
AC、BC
两边高线的交点处
B.在
AC、BC
两边垂直平分线的交点处
C.在
AC、BC
两边中线的交点处
D.在∠A、∠B两内角平分线的交点处
3.如图,直线与交于点O,,下列结论中正确的是(
)
A.
B.
C.是的垂直平分线
D.点P在的垂直平分线上
4.如图,已知线段,分别以点A、B为圆心,大于的长为半径画弧,两弧交于点C和点D,作直线,在上取两点P、M,连接、、、,则下列结论一定正确的是(
)
A.
B.
C.
D.
5.如图,已知,则下列说法中不一定正确的是(
)
A.
B.
C.
D.
6.如图所示,在中,分别以点A和点B为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD.若的周长为10,,则的周长为(
)
A.7
B.10
C.17
D.20
7.如图,在中,是的垂直平分线,,的周长为,则的周长是(
).
A.
B.
C.
D.
8.在等边所在的平面内求一点P,使、、都是等腰三角形,具有这样性质的点P共有(
)个.
A.1
B.4
C.9
D.10
二、填空题
9.和线段AB两个端点距离相等的轨迹是__________________.
10.线段的垂直平分线;经过_______并且_______的______叫做这条线段的垂直平分线(也叫线段的中垂线).
11.如图,△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为14cm,则△ABC的周长为________cm.
12.如图,已知A(0,3),B(2,1),C(2,-3),若点P是△ABC三边垂直平分线的交点,则点P的坐标为___________________.
13.如图,撑伞时,把伞“两侧的伞骨”和支架分别看作、和、,始终有,请大家考虑一下伞杆与B、C的连线的位置关系为________.
14.如图,在中,是的垂直平分线,,则的度数为_______.
15.如图,的两边的垂直平分线分别交于D、E,若,则的度数为_________.
16.△ABC中,若AB﹣AC=2cm,BC的垂直平分线交AB于D点,且△ACD的周长为14cm,则AB=_____,AC=_____.
三、解答题
17.直角三角形的一个锐角为,请将它分成三部分,要求每一部分的大小、形状都相同,画出图形.
18.如图,直线1外有两点A、B,请在直线l上找一点P,使得点P到点A和点B的距离相等.(尺规作图,不写作法,写清结论)
19.证明定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.已知:如图,A为线段外任意一点,且.求证:点A在的垂直平分线上.
20.如图,MN垂直平分线段AB,CD,垂足分别为点E,F,求证:,.
21.如图,平面上的四边形是一只“风筝”的骨架,其中,某同学观察了这只“风筝”的骨架后,认为四边形的两条对角线,垂直,垂足为E,并且,你认为这位同学的判断正确吗?请说明理由.
22.如图,在中,BC边的垂直平分线MN交AC边于点D,交BC边于点E,连接BD.若,的周长为18,求BD的长.
23.已知,如图,中,是角平分线,D是上一点,且交于E,求证:平分.
24.如图,小河边有两个村庄A、B.要在河边建一自来水厂向A村与B村供水.
(1)若要使水厂到A、B村的距离相等,则应选择在哪建厂?
(2)若要使水厂到A、B村的水管最省料,应建在什么地方?(保留作图痕迹,不写作法)
25.如图,在中,,AB的垂直平分线DE交AC于D,垂足为E,若,.
求的度数;
求AC的长度.
试卷第1页,共3页
参考答案
1.A
【解析】∵AC=AD,BC=BD,
∴点A在CD的垂直平分线上,点B在CD的垂直平分线上,
∴AB是CD的垂直平分线.
即AB垂直平分CD.
故选A
2.B
【解析】解:根据线段垂直平分线上的点到线段两个端点的距离相等,
可知超市应建在AC、BC两边垂直平分线的交点处,
故选:B.
3.D
【解析】解:因为直线PO与AB交于点O,且PA=PB,
所以P在线段AB的垂直平分线上,
故选:D.
4.D
【解析】解:由题意可知,直线是线段的垂直平分线,所以.
故选择:D
5.A
【解析】解:∵,
∴垂直平分线段,
∴,,,
故正确,不符合题意;
∴只有选项A不一定正确,符合题意.
故选:
6.C
【解析】首先根据题意可得MN是线段AB的垂直平分线,即可得,又由的周长为10,求得,则可求得的周长为.
答案:C
7.C
【解析】解:∵DE是AC的垂直平分线,
∴AD=CD,AC=2AE=6cm,
又∵△ABD的周长=AB+BD+AD=13cm,
∴AB+BD+CD=13cm,
即AB+BC=13cm,
∴△ABC的周长=AB+BC+AC=13+6=19cm.
故选C.
8.D
【解析】①当点P在三角形的内部时,点P是边AB、BC、AC的垂直平分线的交点,是三角形的外心,如图点.
②当P在三角形的外部时,分别以三角形各顶点为圆心,边长为半径画弧,与垂直平分线的交点有3个,如图,点,共9个.
综上具有这样性质的点P共有10个.
故选:D.
9.线段AB的垂直平分线
【解析】到线段AB两个端点的距离相等的点的轨迹是线段AB的垂直平分线,
故答案为:线段AB的垂直平分线.
10.线段的中点
垂直于这条线段
直线
【解析】解:经过线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
故填:线段的中点,垂直于这条线段,直线.
11.24
【解析】∵DE是AC的垂直平分线
∴AD=CD,AE=EC=5cm,
∴AC=10cm
∵△ABD的周长为14cm
∴AB+BD+AD=14,
△ABC的周长为AB+BC+AC=
AB+
BD+
CD+AC=
AB+BD+AD+AC=14+10=24cm.
12.(-2,-1)
【解析】设p点坐标为(a,b),则有
,
解得:a=
-2,b=-1,
所以P点的坐标为(-2,-1).
故答案为(-2,-1)
13.垂直
【解析】解:如图,连接、,
∵,
∴点A在线段的垂直平分线上,点D在线段的垂直平分线上,
∴根据两点确定一条直线得出直线是线段的垂直平分线,
故答案为:垂直.
14.15°
【解析】解:∵在Rt△ABC中,,
∵DE是AB的垂直平分线
∴∠B=∠BAE
∵∠CAE:∠EAB=4:1
∴6∠B=90°
∴∠B=15°
故答案为:15°.
15.
【解析】解:∵△ABC的两边AB,AC的垂直平分线分别交BC于D,E,
∴DA=DB,EA=EC,
∴∠B=∠DAB,∠C=∠EAC.
∵∠BAC+∠DAE=150°,①
∴∠B+∠C+2∠DAE=150°.
∵∠B+∠C+∠BAC=180°,
∴180°-∠BAC+2∠DAE=150°,
即∠BAC-2∠DAE=30°.②
由①②组成的方程组,
解得∠BAC=110°.
故答案为:110°.
16.AB=8cm
AC=6cm
【解析】根据线段垂直平分线性质求出BD=DC,根据三角形周长AD+BD+AC=AB+AC=14cm,根据已知得出AC=AB-2cm,即可求出AC=6cm,AB=8cm.
故答案为8,6.
17.作图见解析,理由见解析
【解析】解:如图,△ACE,△AEF,△EFB即为所求.
理由如下:
由作图可得:是AB的垂直平分线,
所以每一部分的大小、形状都相同,
18.见解析.
【解析】解:作AB的垂直平分线CD,交直线l于P,
点P为所求
19.见解析
【解析】证明:如图,作于点D,
∵,
∴,
在和中,
∴.
∴,
∴直线是线段的垂直平分线,
∴点A在的垂直平分线上.
20.见解析
【解析】答案:证明:如图,连接EC、ED,
∵MN垂直平分线段AB,∴,,又∵MN垂直平分线段CD,∴,由对称性得,,∴,即,在和中,
∴(SAS),
∴,,
又,∴,即.
易错:证明:∵MN垂直平分线段AB,∴,
∵MN垂直平分线段CD,∴,
∴,.
21.正确,理由见解析
【解析】解:正确理由如下:
∵,
∴点A在的垂直平分线上.
又∵,
∴点C在的垂直平分线上.
∴所在直线为的垂直平分线,
∴.
22.5
【解析】解析:根据线段垂直平分线的性质得到,,根据三角形的周长公式计算即可.
答案:解:∵MN垂直平分BC,∴,,又∵,,又∵的周长为18,∴.∴.
23.见解析
【解析】证明:∵AD=AC,是角平分线,
∴AF垂直平分CD,
∴CF=DF,
∴∠FDC=∠FCD,
∵,
∴∠EDC=∠DCF,
∴∠EDC=FDC,
∴CD平分∠EDF.
24.(1)答案见解析;(2)答案见解析.
【解析】解:(1)作出AB的中垂线与EF的交点M,交点M即为厂址所在位置;
(2)如图所示:作A点关于直线EF的对称点A′,再连接A′B交EF于点N,点N即为所求.
25.(1)(2)6
【解析】垂直平分AB,
,
,
;
,,
,
,
.
.
答案第1页,共2页
答案第1页,共2页
