2021-2022学年八年级数学上册华东师大版13.5.3角平分线同步练习(Word版,含答案解析)
文档属性
| 名称 | 2021-2022学年八年级数学上册华东师大版13.5.3角平分线同步练习(Word版,含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 749.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 22:58:21 | ||
图片预览




文档简介
2021-2022学年八年级数学上册(华东师大版)
13.5.3角平分线-同步练习
时间:60分钟
一、单选题
1.如图,,若,则的度数为(
)
A.
B.
C.
D.
2.如图,在中,,,BD是的平分线,设、的面积分别为、,则(
)
A.
B.
C.
D.
3.如图,直线,相交于点,射线平分,若,则等于(
)
A.
B.
C.
D.
4.如图,直线a,b,c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有(
)
A.一处
B.两处
C.三处
D.四处
5.如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是(
)
A.80°
B.90°
C.100°
D.110°
6.如图,∠AOB=∠BOD,OC平分∠AOD,下列四个等式中正确的是( )
①∠BOC=∠AOB;②∠DOC=2∠BOC;③∠COB=∠BOA;④∠COD=3∠COB.
A.①②
B.②③
C.③④
D.①④
7.如图所示,直线,交于点,射线OM平分.若,则等于(
)
A.
B.
C.
D.
8.如图所示,在中,,,AD平分,交AC的延长线F,E为垂足.则有:①;②;③;④;⑤,其中正确结论的个数是(
)
A.1
B.2
C.3
D.4
二、填空题
9.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是_____.
10.如图,已知,且,则点C在________的平分线上,点A在________的平分线上.
11.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是_______.
12.已知:如图,给出下列论断:
①;②平分;③.
以上面论断中的两个作为题设,再从余下的论断作为结论,并用“如果……,那么……”的形式写出一个真命题.
答:________________________________________.
13.如图,直线、相交于点O,射线平分,若,则
的度数为__________.
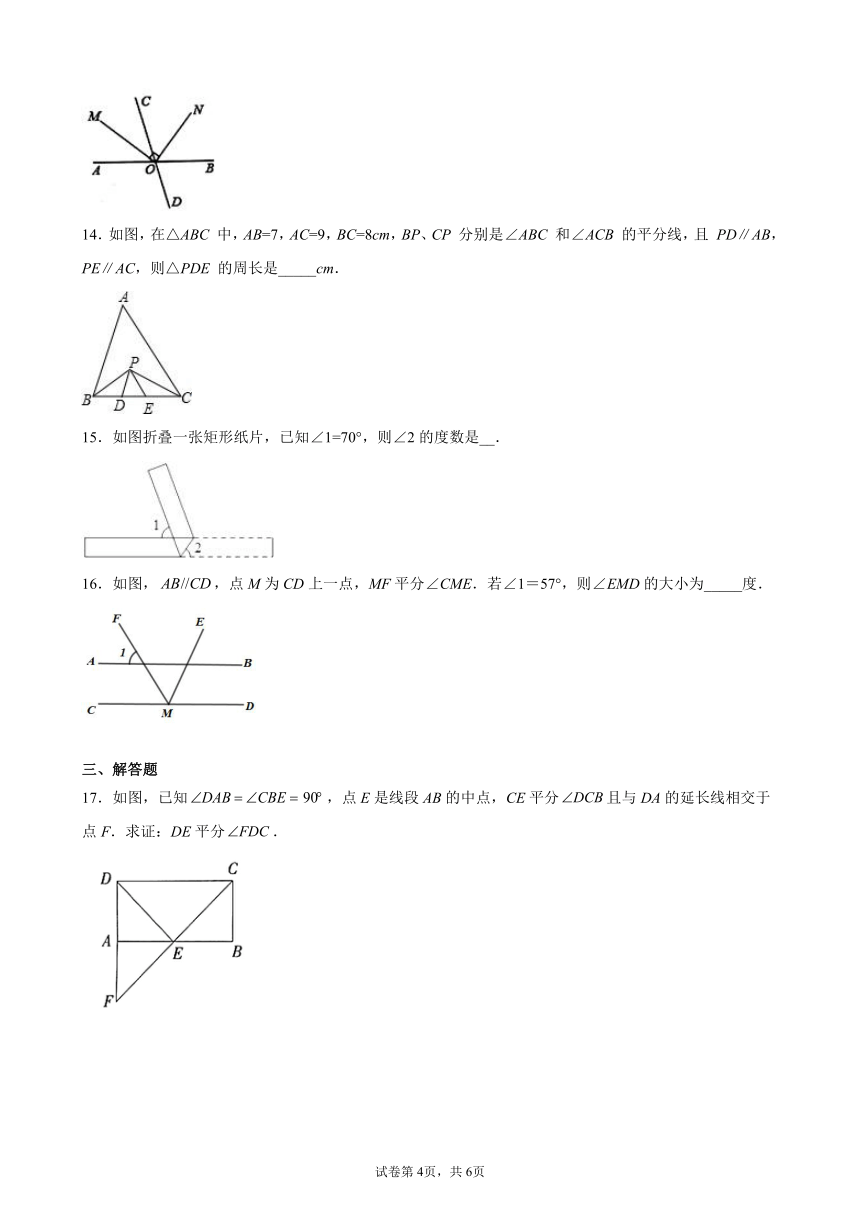
14.如图,在△ABC
中,AB=7,AC=9,BC=8cm,BP、CP
分别是∠ABC
和∠ACB
的平分线,且
PD∥AB,PE∥AC,则△PDE
的周长是_____cm.
15.如图折叠一张矩形纸片,已知∠1=70°,则∠2的度数是__.
16.如图,,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为_____度.
三、解答题
17.如图,已知,点E是线段AB的中点,CE平分且与DA的延长线相交于点F.求证:DE平分.
18.已知:如图,,EG平分,,,求的度数.
19.如图,在三角形中,,,分别是三边上的点,且平分,.若,求的度数.
20.例1
如图所示,已知,DM平分,AM平分.求证:M是BC的中点.
21.如图,在△ABC中,AC=BC,∠C=90°,AD是∠BAC的平分线,DE⊥AB,垂足为E
(1)若CD=6,求AC的长;
(2)求证:AB-AC=CD
22.如图,AD是的角平分线,EF是AD的垂直平分线.
求证:(1);
(2);
(3).
23.已知:如图,平分平分,求的度数.
解:过P点作交于点M.
∵,(________________)
∴________.(________________)
∵,
∴________________,(两直线平行,内错角相等)
且________.(平行于同一直线的两直线也互相平行)
∴________.(两直线平行,内错角相等)
∵平分平分,(
)
∴________,________.(
)
∴(
)
∴.(
)
试卷第1页,共3页
参考答案
1.C
【解析】∵,
∴平分,
∵,
∴,
∴,
故选:C.
2.A
【解析】如图,过点D作交AB于点E,由BD是的平分线,得,由于,,又∵,∴.
答案:A
3.C
【解析】解:平分,,
,
,
答案:.
4.D
【解析】解:如图所示,可供选择的地址有4个,
故选:D
5.C
【解析】解:∵∠A+∠B+∠ADC+∠DCB=360°,∠A+∠B=200°,
∴∠ADC+∠DCB=160°.
又∵∠ADC、∠DCB的平分线相交于点O,
∴∠ODC=∠ADC,∠OCD=,
∴∠ODC+∠OCD=80°,
∴∠COD=180°﹣(∠ODC+∠OCD)=100°.
故选C.
6.C
【解析】解:因为∠AOB=∠BOD,
所以∠AOB=∠AOD,
因为OC平分∠AOD,
所以∠AOC=∠DOC=∠AOD,
所以∠BOC=∠AOC-∠AOB=∠AOD-∠AOD=∠AOD=∠AOB,
故①错误,③正确;
因为∠DOC=∠AOD,∠BOC=∠AOD,
所以∠DOC=3∠BOC
故②错误,④正确.
7.A
【解析】∵OM平分,,
,
.
故选:.
8.D
【解析】解:∵,
∴
∵AD平分
∴
∵
∴
∴
∴AD=BF,CF=CD,故①②正确;
∵CD=CF,
∴AC+CD=AC+CF=AF
∵
∵
∴AF=AB,即AC+CD=AB,故③正确;
由③可知,三角形ABF是等腰三角形,
∵
∴
若,则与②中结论相矛盾,故④错误;
∵三角形ABF是等腰三角形,
∵
∴
∴BF=2BE,故⑤正确;综上所述,正确的选项有4个.
故选:D.
9.3
【解析】解:如图,过点D作DF⊥AC于F,
∵AD是△ABC中∠BAC的角平分线,DE⊥AB,
∴DE=DF,
由图可知,S△ABC=S△ABD+S△ACD,
×4×2+×AC×2=7,
解得:AC=3.
故答案为:3.
10.
【解析】解:连接AC,
∵,,
∴AC平分,
∴点C在的平分线上,,
∵,
∴,
∴,即AC平分,
∴点A在的平分线上,
故答案为:,.
11.30
【解析】解:作于E,如图,
由作法得AP平分∠BAC,
∴,
∴△ABD的面积=.
故答案为:30.
12.如果,平分,那么(答案不唯一)
【解析】证明:∵,
∴,
∵平分,
∴,
∴.
故答案为:如果,平分,那么.
13.
【解析】解:∵射线OM平分,
∴∠AOM=35°
∵∠MON=90°
根据平角定义可得=55°
故答案为55°.
14.8
【解析】∵BP、CP
分别是∠ABC
和∠ACB
的角平分线,
∴∠ABP=∠PBD,∠ACP=∠PCE,
∵PD∥AB,PE∥AC,
∴∠ABP=∠BPD,∠ACP=∠CPE,
∴∠PBD=∠BPD,∠PCE=∠CPE,
∴BD=PD,CE=PE,
∴△PDE
的周长=PD+DE+PE=BD+DE+EC=BC=8cm.
故答案是:8.
15.55°
【解析】
,
,
.
16.
【解析】∵AB∥CD,
∴∠CMF=∠1=57°,
∵MF平分∠CME,
∴∠CME=2∠CMF=114°,
∴∠EMD=180°-∠CME=66°,
故答案为:66.
17.见解析
【解析】证明:如图,过点E作于点H,
∵CE平分,,∴,
∵点E是线段AB的中点,
∴,∴,
又∵,,∴DE平分.
18.
【解析】解:∵,
∴,
∴,
∵,
∴,即,①
∵,②
∴由①②可得,
∵EG平分,
∴,
∴.
19.80°
【解析】解:,,
,
平分,
,
.
20.见解析
【解析】证明:如图,过点M作,
∵DM平分,,,∴,又∵AM平分,,∴,∴,∴M是BC的中点.
21.(1)AC=BC=12+6;(2)见解析.
【解析】(1)∵∠C=90°,AD是∠BAC的角平分线,DE⊥AB,
∴DE=CD=6,
∵在△ABC中,AC=BC,∠C=90°,
∴∠CAB=∠B=45°,
∴∠EDB=∠B=45°,
在Rt△BDE中,由勾股定理得:BD=12
∴AC=BC=CD+BD=12+6;
(2)∵AD是∠BAC的角平分线,
∴∠CAD=∠EAD,
∵∠C=90°,
∴AC⊥BC,
∵DE⊥AB,
∴∠ADC=∠ADE,
又∵AD=AD,
∴△ADC≌△ADE,
∴AE=AC,
∵CD=DE,DE=BE,
∴CD=BE,
∴AB-AC=AB-AE=BE=CD,
即:AB-AC=CD.
22.(1)见解析;(2)见解析;(3)见解析
【解析】证明:(1)如图,连接AE,设AD与EF相交于点Q,
∵EF是AD的垂直平分线,
∴,,
在和中,
∵
∴(SSS),
∴;
(2)∵EF是AD的垂直平分线,
∴,
在和中,
∵
∴(SSS),
∴,
∵AD是的角平分线,
∴,
∴,
∴;
(3)由(1)知,
,
∴,
又∵,
∴,
∵,
∴.
易错:证明:(1)∵EF是AD的垂直平分线,
∴,在和中,
∴(SAS),
∴.
23.已知,,两直线平行,同旁内角互补,,,4,已知,,角的平分线的定义,等式的性质,等量代换
【解析】解:过P点作交于点M.
∵,(已知)
∴DCA.(两直线平行,同旁内角互补)
∵,
∴∠1=∠2,(两直线平行,内错角相等)
且CD.(平行于同一直线的两直线也互相平行)
∴4.(两直线平行,内错角相等)
∵平分,平分,(已知)
∴,.(角的平分线的定义)
∴(等式的性质)
∴.(等量代换)
故答案为:已知,
DCA,两直线平行,同旁内角互补,∠1=∠2,
CD,4,已知,,,角的平分线的定义,等式的性质,等量代换.
答案第1页,共2页
答案第1页,共2页
13.5.3角平分线-同步练习
时间:60分钟
一、单选题
1.如图,,若,则的度数为(
)
A.
B.
C.
D.
2.如图,在中,,,BD是的平分线,设、的面积分别为、,则(
)
A.
B.
C.
D.
3.如图,直线,相交于点,射线平分,若,则等于(
)
A.
B.
C.
D.
4.如图,直线a,b,c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有(
)
A.一处
B.两处
C.三处
D.四处
5.如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是(
)
A.80°
B.90°
C.100°
D.110°
6.如图,∠AOB=∠BOD,OC平分∠AOD,下列四个等式中正确的是( )
①∠BOC=∠AOB;②∠DOC=2∠BOC;③∠COB=∠BOA;④∠COD=3∠COB.
A.①②
B.②③
C.③④
D.①④
7.如图所示,直线,交于点,射线OM平分.若,则等于(
)
A.
B.
C.
D.
8.如图所示,在中,,,AD平分,交AC的延长线F,E为垂足.则有:①;②;③;④;⑤,其中正确结论的个数是(
)
A.1
B.2
C.3
D.4
二、填空题
9.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是_____.
10.如图,已知,且,则点C在________的平分线上,点A在________的平分线上.
11.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是_______.
12.已知:如图,给出下列论断:
①;②平分;③.
以上面论断中的两个作为题设,再从余下的论断作为结论,并用“如果……,那么……”的形式写出一个真命题.
答:________________________________________.
13.如图,直线、相交于点O,射线平分,若,则
的度数为__________.
14.如图,在△ABC
中,AB=7,AC=9,BC=8cm,BP、CP
分别是∠ABC
和∠ACB
的平分线,且
PD∥AB,PE∥AC,则△PDE
的周长是_____cm.
15.如图折叠一张矩形纸片,已知∠1=70°,则∠2的度数是__.
16.如图,,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为_____度.
三、解答题
17.如图,已知,点E是线段AB的中点,CE平分且与DA的延长线相交于点F.求证:DE平分.
18.已知:如图,,EG平分,,,求的度数.
19.如图,在三角形中,,,分别是三边上的点,且平分,.若,求的度数.
20.例1
如图所示,已知,DM平分,AM平分.求证:M是BC的中点.
21.如图,在△ABC中,AC=BC,∠C=90°,AD是∠BAC的平分线,DE⊥AB,垂足为E
(1)若CD=6,求AC的长;
(2)求证:AB-AC=CD
22.如图,AD是的角平分线,EF是AD的垂直平分线.
求证:(1);
(2);
(3).
23.已知:如图,平分平分,求的度数.
解:过P点作交于点M.
∵,(________________)
∴________.(________________)
∵,
∴________________,(两直线平行,内错角相等)
且________.(平行于同一直线的两直线也互相平行)
∴________.(两直线平行,内错角相等)
∵平分平分,(
)
∴________,________.(
)
∴(
)
∴.(
)
试卷第1页,共3页
参考答案
1.C
【解析】∵,
∴平分,
∵,
∴,
∴,
故选:C.
2.A
【解析】如图,过点D作交AB于点E,由BD是的平分线,得,由于,,又∵,∴.
答案:A
3.C
【解析】解:平分,,
,
,
答案:.
4.D
【解析】解:如图所示,可供选择的地址有4个,
故选:D
5.C
【解析】解:∵∠A+∠B+∠ADC+∠DCB=360°,∠A+∠B=200°,
∴∠ADC+∠DCB=160°.
又∵∠ADC、∠DCB的平分线相交于点O,
∴∠ODC=∠ADC,∠OCD=,
∴∠ODC+∠OCD=80°,
∴∠COD=180°﹣(∠ODC+∠OCD)=100°.
故选C.
6.C
【解析】解:因为∠AOB=∠BOD,
所以∠AOB=∠AOD,
因为OC平分∠AOD,
所以∠AOC=∠DOC=∠AOD,
所以∠BOC=∠AOC-∠AOB=∠AOD-∠AOD=∠AOD=∠AOB,
故①错误,③正确;
因为∠DOC=∠AOD,∠BOC=∠AOD,
所以∠DOC=3∠BOC
故②错误,④正确.
7.A
【解析】∵OM平分,,
,
.
故选:.
8.D
【解析】解:∵,
∴
∵AD平分
∴
∵
∴
∴
∴AD=BF,CF=CD,故①②正确;
∵CD=CF,
∴AC+CD=AC+CF=AF
∵
∵
∴AF=AB,即AC+CD=AB,故③正确;
由③可知,三角形ABF是等腰三角形,
∵
∴
若,则与②中结论相矛盾,故④错误;
∵三角形ABF是等腰三角形,
∵
∴
∴BF=2BE,故⑤正确;综上所述,正确的选项有4个.
故选:D.
9.3
【解析】解:如图,过点D作DF⊥AC于F,
∵AD是△ABC中∠BAC的角平分线,DE⊥AB,
∴DE=DF,
由图可知,S△ABC=S△ABD+S△ACD,
×4×2+×AC×2=7,
解得:AC=3.
故答案为:3.
10.
【解析】解:连接AC,
∵,,
∴AC平分,
∴点C在的平分线上,,
∵,
∴,
∴,即AC平分,
∴点A在的平分线上,
故答案为:,.
11.30
【解析】解:作于E,如图,
由作法得AP平分∠BAC,
∴,
∴△ABD的面积=.
故答案为:30.
12.如果,平分,那么(答案不唯一)
【解析】证明:∵,
∴,
∵平分,
∴,
∴.
故答案为:如果,平分,那么.
13.
【解析】解:∵射线OM平分,
∴∠AOM=35°
∵∠MON=90°
根据平角定义可得=55°
故答案为55°.
14.8
【解析】∵BP、CP
分别是∠ABC
和∠ACB
的角平分线,
∴∠ABP=∠PBD,∠ACP=∠PCE,
∵PD∥AB,PE∥AC,
∴∠ABP=∠BPD,∠ACP=∠CPE,
∴∠PBD=∠BPD,∠PCE=∠CPE,
∴BD=PD,CE=PE,
∴△PDE
的周长=PD+DE+PE=BD+DE+EC=BC=8cm.
故答案是:8.
15.55°
【解析】
,
,
.
16.
【解析】∵AB∥CD,
∴∠CMF=∠1=57°,
∵MF平分∠CME,
∴∠CME=2∠CMF=114°,
∴∠EMD=180°-∠CME=66°,
故答案为:66.
17.见解析
【解析】证明:如图,过点E作于点H,
∵CE平分,,∴,
∵点E是线段AB的中点,
∴,∴,
又∵,,∴DE平分.
18.
【解析】解:∵,
∴,
∴,
∵,
∴,即,①
∵,②
∴由①②可得,
∵EG平分,
∴,
∴.
19.80°
【解析】解:,,
,
平分,
,
.
20.见解析
【解析】证明:如图,过点M作,
∵DM平分,,,∴,又∵AM平分,,∴,∴,∴M是BC的中点.
21.(1)AC=BC=12+6;(2)见解析.
【解析】(1)∵∠C=90°,AD是∠BAC的角平分线,DE⊥AB,
∴DE=CD=6,
∵在△ABC中,AC=BC,∠C=90°,
∴∠CAB=∠B=45°,
∴∠EDB=∠B=45°,
在Rt△BDE中,由勾股定理得:BD=12
∴AC=BC=CD+BD=12+6;
(2)∵AD是∠BAC的角平分线,
∴∠CAD=∠EAD,
∵∠C=90°,
∴AC⊥BC,
∵DE⊥AB,
∴∠ADC=∠ADE,
又∵AD=AD,
∴△ADC≌△ADE,
∴AE=AC,
∵CD=DE,DE=BE,
∴CD=BE,
∴AB-AC=AB-AE=BE=CD,
即:AB-AC=CD.
22.(1)见解析;(2)见解析;(3)见解析
【解析】证明:(1)如图,连接AE,设AD与EF相交于点Q,
∵EF是AD的垂直平分线,
∴,,
在和中,
∵
∴(SSS),
∴;
(2)∵EF是AD的垂直平分线,
∴,
在和中,
∵
∴(SSS),
∴,
∵AD是的角平分线,
∴,
∴,
∴;
(3)由(1)知,
,
∴,
又∵,
∴,
∵,
∴.
易错:证明:(1)∵EF是AD的垂直平分线,
∴,在和中,
∴(SAS),
∴.
23.已知,,两直线平行,同旁内角互补,,,4,已知,,角的平分线的定义,等式的性质,等量代换
【解析】解:过P点作交于点M.
∵,(已知)
∴DCA.(两直线平行,同旁内角互补)
∵,
∴∠1=∠2,(两直线平行,内错角相等)
且CD.(平行于同一直线的两直线也互相平行)
∴4.(两直线平行,内错角相等)
∵平分,平分,(已知)
∴,.(角的平分线的定义)
∴(等式的性质)
∴.(等量代换)
故答案为:已知,
DCA,两直线平行,同旁内角互补,∠1=∠2,
CD,4,已知,,,角的平分线的定义,等式的性质,等量代换.
答案第1页,共2页
答案第1页,共2页
