23.1.2平行线分线段成比例-同步练习-2021-2022学年九年级数学上册华东师大版(word版含答案)
文档属性
| 名称 | 23.1.2平行线分线段成比例-同步练习-2021-2022学年九年级数学上册华东师大版(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 485.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 07:11:35 | ||
图片预览


文档简介
2021-2022学年九年级数学上册(华东师大版)
23.1.2平行线分线段成比例-同步练习
时间:60分钟
一、单选题
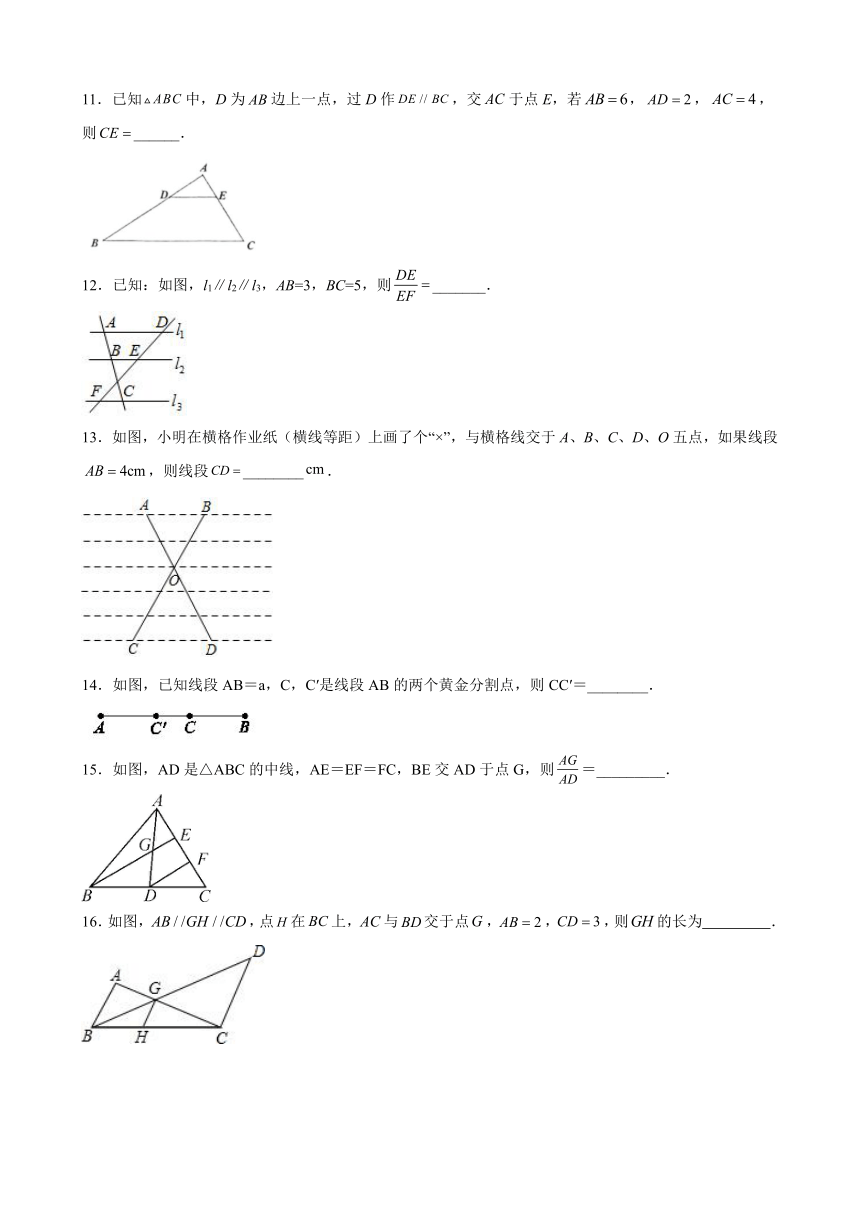
1.如图,在的边上任取两点B,C,过B作的平行线交于N,过N作的平行线交于D.若,则的值为(
).
A.
B.
C.2
D.3
2.如图,直线,那么的值是(
)
A.
B.1
C.
D.2
3.如图,已知,那么(
)
A.3
B.4
C.5
D.6
4.如图,;;下列比例式正确的是(
).
A.
B.
C.
D.
5.如图,在△ABC中,DE∥BC,若,则等于(
)
A.
B.
C.
D.
6.如图,在△ABC中,DE∥BC,EF∥AB,AD:BD=5:3,CF=6,则DE的长为( )
A.6
B.8
C.10
D.12
7.已知线段a、b、c,求作线段,下列作法中正确的是(
)
A.B.C.D.
8.如图,点G、F分别是的边、上的点,的延长线与的延长线相交于点A,交于点E,则下列结论错误的是(
)
A.
B.
C.
D.
二、填空题
9.平行于三角形一边的直线截其他两边,所得的______.
10.如图,在中,DE∥BC,DF∥AC,如果,则_________.
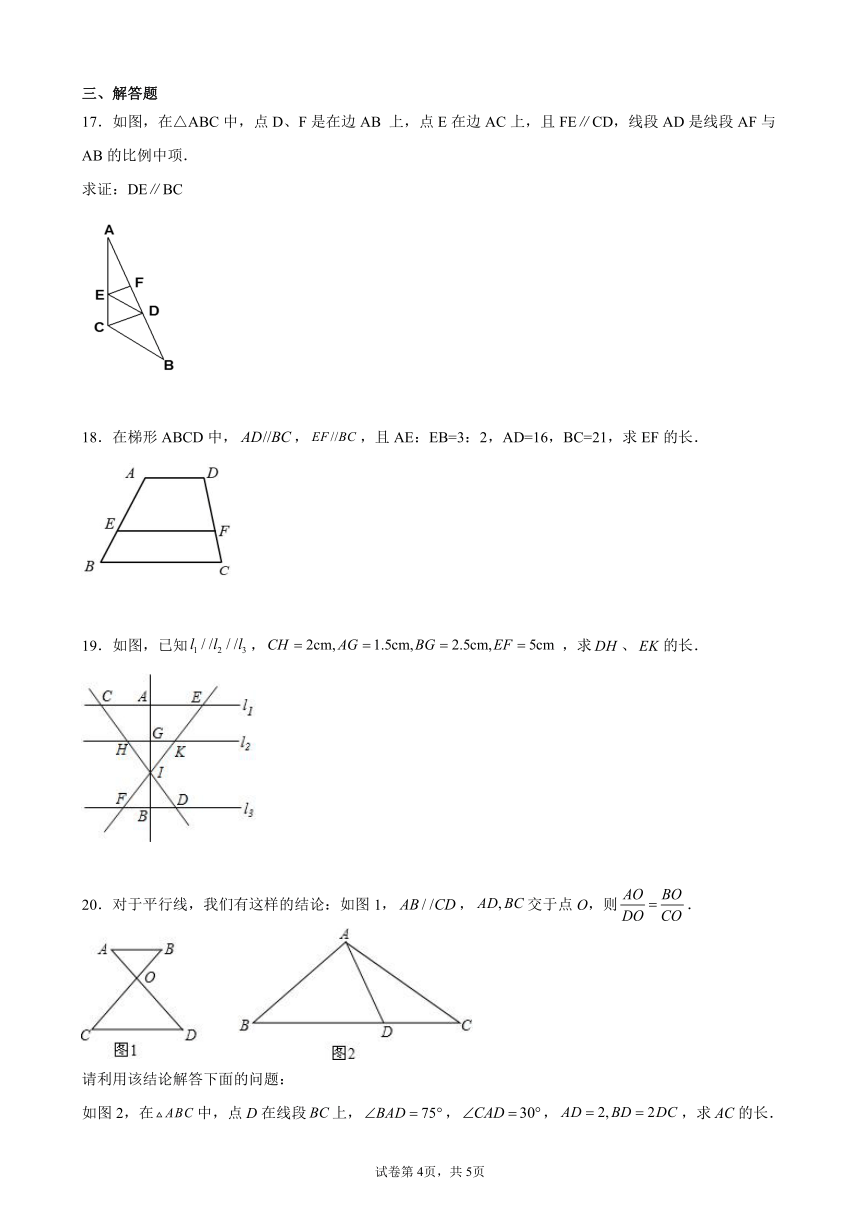
11.已知中,D为边上一点,过D作,交于点E,若,,,则______.
12.已知:如图,l1∥l2∥l3,AB=3,BC=5,则_______.
13.如图,小明在横格作业纸(横线等距)上画了个“×”,与横格线交于A、B、C、D、O五点,如果线段,则线段________.
14.如图,已知线段AB=a,C,C′是线段AB的两个黄金分割点,则CC′=________.
15.如图,AD是△ABC的中线,AE=EF=FC,BE交AD于点G,则=_________.
16.如图,,点在上,与交于点,,,则的长为
.
三、解答题
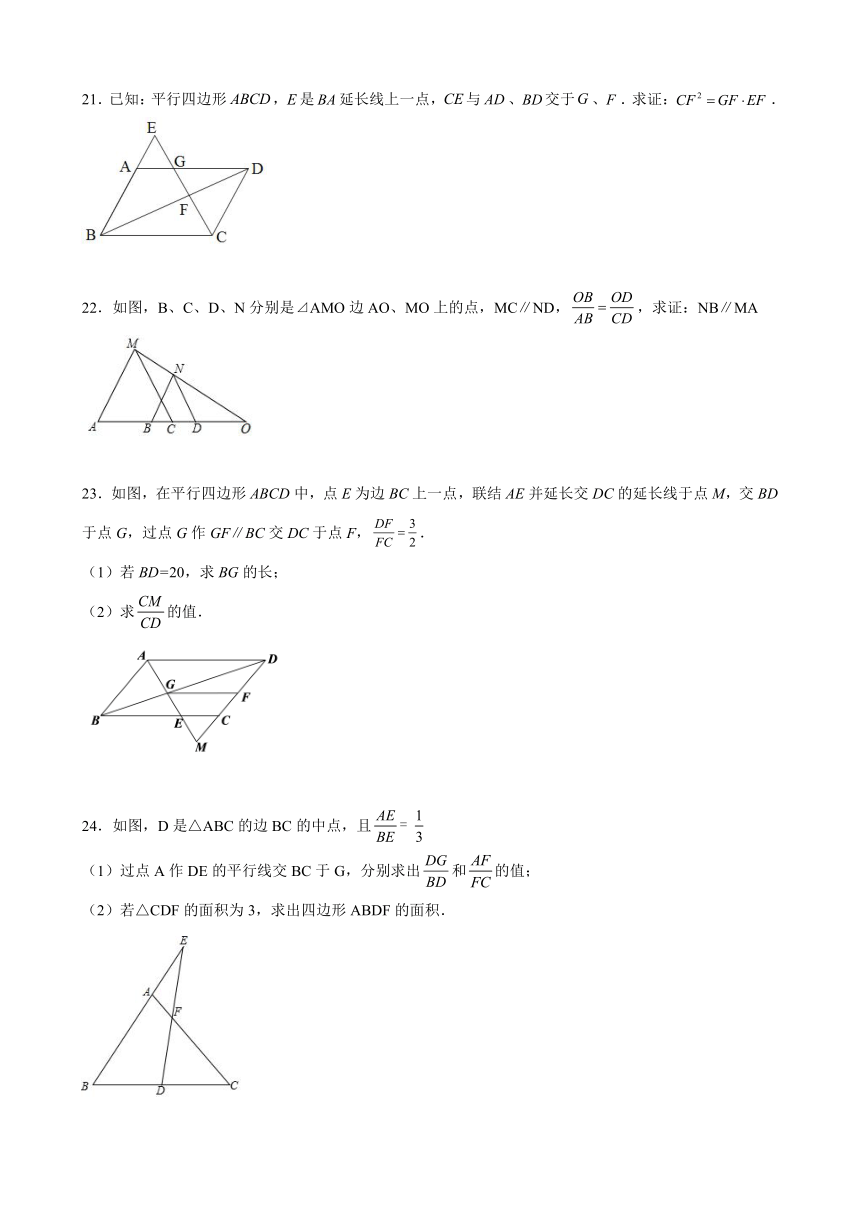
17.如图,在△ABC中,点D、F是在边AB
上,点E在边AC上,且FE∥CD,线段AD是线段AF与AB的比例中项.
求证:DE∥BC
18.在梯形ABCD中,,,且AE:EB=3:2,AD=16,BC=21,求EF的长.
19.如图,已知,,求、的长.
20.对于平行线,我们有这样的结论:如图1,,交于点O,则.
请利用该结论解答下面的问题:
如图2,在中,点D在线段上,,,,求的长.
21.已知:平行四边形,是延长线上一点,与、交于、.求证:.
22.如图,B、C、D、N分别是⊿AMO边AO、MO上的点,MC∥ND,,求证:NB∥MA
23.如图,在平行四边形ABCD中,点E为边BC上一点,联结AE并延长交DC的延长线于点M,交BD于点G,过点G作GF∥BC交DC于点F,.
(1)若BD=20,求BG的长;
(2)求的值.
24.如图,D是△ABC的边BC的中点,且
(1)过点A作DE的平行线交BC于G,分别求出和的值;
(2)若△CDF的面积为3,求出四边形ABDF的面积.
试卷第1页,共3页
参考答案
1.B
【解析】解:∵AM∥BN,
∴,
又∵MC∥ND,
∴,
故选B.
2.D
【解析】解:∵,
∴,
∵,
∴,
∴AB+BC=3BC,
∴AB=2BC,
∴,
∵,
∴,
∴,
经检验符合题意.
故选择D.
3.B
【解析】解:∵AB∥CD,
∴;
∵AO=2,CO=6,BO=3,
∴,
解得:DO=4,
故选B.
4.A
【解析】解:∵DE∥BC,
∴,,
∵EF∥AB,
∴,,
∴即,
故选A.
5.C
【解析】:∵DE∥BC,
∴,
故选C.
6.C
【解析】解:DE∥BC,EF∥AB
四边形BFED是平行四边形
DE∥BC
AD:BD=5:3
又EF∥AB
又
CF=6
即DE=10
故选C
7.D
【解析】由A得,,则x=,A错误;
由B得,,则x=,B错误;
由C得,,则x=,C错误;
由D得,,则x=,D正确.
故选:D.
8.C
【解析】解:∵交GA于点E,
,,,,
所以,A,B,D正确,
故选:C.
9.对应线段成比例
【解析】平行线分线段成比例的推论:平行于三角形一边的直线截其他两边,所得的对应线段成比例,
故答案为:对应线段成比例.
10.
【解析】解:
故答案为:
11.
【解析】解:∵DE∥BC,
∴,
∵AB=6,
AD=2,
AC=4,
∴,
∴,
∴,
故答案为:.
12.
【解析】解:∵直线l1∥l2∥l3,AB=3,BC=5,
∴,
故答案为:.
13.6
【解析】解:如图所示,过点O作OE⊥AB于E,OF⊥CD于F,
∴∠DEA=∠OFC=90°,
∵AB∥CD,
∴E、O、F三点共线,
∴,,
∴,
∵横线等距,
∴
∴,
∴,
故答案为:6.
14.
【解析】∵线段AB=a,C,C′是线段AB的两个黄金分割点,
∴较短线段AC′=BC=a,
则CC′=AB-AC′-BC=a-2×a=(-2)a.
故答案是:(-2)a.
15.
【解析】解:∵AD是△ABC的中线,
∴BD=CD,
∵AE=EF=FC,
∴F是CE中点,
∴DF∥GE,
∴=.
故答案为.
16.
【解析】解:,
,
即①,
,
,
即②,
①②,
得,
,
,
解得.
故答案为:
17.证明过程见解析
【解析】∵FE∥CD,
∴,
∵AD是线段AF与AB的比例中项,
∴,
∴,
∴DE∥BC.
18.EF的长为19.
【解析】如图,过点A作,分别交EF于点G,BC于点H,
∵,,
∴四边形AHCD是平行四边形,
∴,
同理可得:,
∵,
∴,
∵,
∴,
,
∴,
∴,
解得,
∴.
19.,.
【解析】解:∵
∴,
∴,
∴,
∴,,
设,
∴,
解得.
∴.
20.3
【解析】解:过点C作CE∥AB交AD的延长线于E,
则=,又BD=2DC,
∴
∵AD=2,
∴DE=1,
∵CE∥AB,
∴∠E=∠BAD=75°,又∠CAD=30°,
∴∠ACE=∠E=75°,
∴AC=AE=AD
+
DE
=3.
21.详见解析
【解析】解:∵四边形是平行四边形,
∴,.
∴,
∴,
即.
22.证明过程见解析
【解析】解:∵MC∥ND
∴
∵
∴
∴NB∥MA
23.(1)8;(2)
【解析】(1)
∵GF∥BC,
∴,
∵BD=20,,
∴
;
(2)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴,
∴,
∴,
∴.
24.(1),;(2)5
【解析】解:(1)过点A作AG∥ED交BC于点G,如图1所示.
∵AG∥ED,
∴
∵D是△ABC的边BC的中点,
∴,
∴
(2)连接BF,如图2所示.
∵BD=CD,
∴S△BDF=S△CDF=3.
又∵,
∴S△ABF=S△BCF=2,
∴S四边形ABDF=S△ABF+S△BDF=2+3=5.
答案第1页,共2页
答案第1页,共2页
23.1.2平行线分线段成比例-同步练习
时间:60分钟
一、单选题
1.如图,在的边上任取两点B,C,过B作的平行线交于N,过N作的平行线交于D.若,则的值为(
).
A.
B.
C.2
D.3
2.如图,直线,那么的值是(
)
A.
B.1
C.
D.2
3.如图,已知,那么(
)
A.3
B.4
C.5
D.6
4.如图,;;下列比例式正确的是(
).
A.
B.
C.
D.
5.如图,在△ABC中,DE∥BC,若,则等于(
)
A.
B.
C.
D.
6.如图,在△ABC中,DE∥BC,EF∥AB,AD:BD=5:3,CF=6,则DE的长为( )
A.6
B.8
C.10
D.12
7.已知线段a、b、c,求作线段,下列作法中正确的是(
)
A.B.C.D.
8.如图,点G、F分别是的边、上的点,的延长线与的延长线相交于点A,交于点E,则下列结论错误的是(
)
A.
B.
C.
D.
二、填空题
9.平行于三角形一边的直线截其他两边,所得的______.
10.如图,在中,DE∥BC,DF∥AC,如果,则_________.
11.已知中,D为边上一点,过D作,交于点E,若,,,则______.
12.已知:如图,l1∥l2∥l3,AB=3,BC=5,则_______.
13.如图,小明在横格作业纸(横线等距)上画了个“×”,与横格线交于A、B、C、D、O五点,如果线段,则线段________.
14.如图,已知线段AB=a,C,C′是线段AB的两个黄金分割点,则CC′=________.
15.如图,AD是△ABC的中线,AE=EF=FC,BE交AD于点G,则=_________.
16.如图,,点在上,与交于点,,,则的长为
.
三、解答题
17.如图,在△ABC中,点D、F是在边AB
上,点E在边AC上,且FE∥CD,线段AD是线段AF与AB的比例中项.
求证:DE∥BC
18.在梯形ABCD中,,,且AE:EB=3:2,AD=16,BC=21,求EF的长.
19.如图,已知,,求、的长.
20.对于平行线,我们有这样的结论:如图1,,交于点O,则.
请利用该结论解答下面的问题:
如图2,在中,点D在线段上,,,,求的长.
21.已知:平行四边形,是延长线上一点,与、交于、.求证:.
22.如图,B、C、D、N分别是⊿AMO边AO、MO上的点,MC∥ND,,求证:NB∥MA
23.如图,在平行四边形ABCD中,点E为边BC上一点,联结AE并延长交DC的延长线于点M,交BD于点G,过点G作GF∥BC交DC于点F,.
(1)若BD=20,求BG的长;
(2)求的值.
24.如图,D是△ABC的边BC的中点,且
(1)过点A作DE的平行线交BC于G,分别求出和的值;
(2)若△CDF的面积为3,求出四边形ABDF的面积.
试卷第1页,共3页
参考答案
1.B
【解析】解:∵AM∥BN,
∴,
又∵MC∥ND,
∴,
故选B.
2.D
【解析】解:∵,
∴,
∵,
∴,
∴AB+BC=3BC,
∴AB=2BC,
∴,
∵,
∴,
∴,
经检验符合题意.
故选择D.
3.B
【解析】解:∵AB∥CD,
∴;
∵AO=2,CO=6,BO=3,
∴,
解得:DO=4,
故选B.
4.A
【解析】解:∵DE∥BC,
∴,,
∵EF∥AB,
∴,,
∴即,
故选A.
5.C
【解析】:∵DE∥BC,
∴,
故选C.
6.C
【解析】解:DE∥BC,EF∥AB
四边形BFED是平行四边形
DE∥BC
AD:BD=5:3
又EF∥AB
又
CF=6
即DE=10
故选C
7.D
【解析】由A得,,则x=,A错误;
由B得,,则x=,B错误;
由C得,,则x=,C错误;
由D得,,则x=,D正确.
故选:D.
8.C
【解析】解:∵交GA于点E,
,,,,
所以,A,B,D正确,
故选:C.
9.对应线段成比例
【解析】平行线分线段成比例的推论:平行于三角形一边的直线截其他两边,所得的对应线段成比例,
故答案为:对应线段成比例.
10.
【解析】解:
故答案为:
11.
【解析】解:∵DE∥BC,
∴,
∵AB=6,
AD=2,
AC=4,
∴,
∴,
∴,
故答案为:.
12.
【解析】解:∵直线l1∥l2∥l3,AB=3,BC=5,
∴,
故答案为:.
13.6
【解析】解:如图所示,过点O作OE⊥AB于E,OF⊥CD于F,
∴∠DEA=∠OFC=90°,
∵AB∥CD,
∴E、O、F三点共线,
∴,,
∴,
∵横线等距,
∴
∴,
∴,
故答案为:6.
14.
【解析】∵线段AB=a,C,C′是线段AB的两个黄金分割点,
∴较短线段AC′=BC=a,
则CC′=AB-AC′-BC=a-2×a=(-2)a.
故答案是:(-2)a.
15.
【解析】解:∵AD是△ABC的中线,
∴BD=CD,
∵AE=EF=FC,
∴F是CE中点,
∴DF∥GE,
∴=.
故答案为.
16.
【解析】解:,
,
即①,
,
,
即②,
①②,
得,
,
,
解得.
故答案为:
17.证明过程见解析
【解析】∵FE∥CD,
∴,
∵AD是线段AF与AB的比例中项,
∴,
∴,
∴DE∥BC.
18.EF的长为19.
【解析】如图,过点A作,分别交EF于点G,BC于点H,
∵,,
∴四边形AHCD是平行四边形,
∴,
同理可得:,
∵,
∴,
∵,
∴,
,
∴,
∴,
解得,
∴.
19.,.
【解析】解:∵
∴,
∴,
∴,
∴,,
设,
∴,
解得.
∴.
20.3
【解析】解:过点C作CE∥AB交AD的延长线于E,
则=,又BD=2DC,
∴
∵AD=2,
∴DE=1,
∵CE∥AB,
∴∠E=∠BAD=75°,又∠CAD=30°,
∴∠ACE=∠E=75°,
∴AC=AE=AD
+
DE
=3.
21.详见解析
【解析】解:∵四边形是平行四边形,
∴,.
∴,
∴,
即.
22.证明过程见解析
【解析】解:∵MC∥ND
∴
∵
∴
∴NB∥MA
23.(1)8;(2)
【解析】(1)
∵GF∥BC,
∴,
∵BD=20,,
∴
;
(2)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴,
∴,
∴,
∴.
24.(1),;(2)5
【解析】解:(1)过点A作AG∥ED交BC于点G,如图1所示.
∵AG∥ED,
∴
∵D是△ABC的边BC的中点,
∴,
∴
(2)连接BF,如图2所示.
∵BD=CD,
∴S△BDF=S△CDF=3.
又∵,
∴S△ABF=S△BCF=2,
∴S四边形ABDF=S△ABF+S△BDF=2+3=5.
答案第1页,共2页
答案第1页,共2页
