23.3.4相似三角形的应用-同步练习-2021-2022学年九年级数学上册 华东师大版(word版含答案)
文档属性
| 名称 | 23.3.4相似三角形的应用-同步练习-2021-2022学年九年级数学上册 华东师大版(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 556.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 07:18:33 | ||
图片预览



文档简介
2021-2022学年九年级数学上册(华东师大版)
23.3.4相似三角形的应用-同步练习
时间:60分钟
一、单选题
1.如图,A,B两点被一河隔开,为了测量A,B两点间的距离,小明过点B作BF⊥AB,在BF上取两点C,D,使BC=2CD,过点D作DE⊥BF且使点A,C,E在同一条直线上,测得DE=20m,则A,B两点间的距离是(
)
A.60m
B.50m
C.40m
D.30m
2.某同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立米长的标杆测得其影厂为米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为米和米,则学校旗杆的高度为(
)米.
A.
B.
C.
D.
3.小刚身高1.7m,测得他站立在阳光下的影子长为0.85m,紧接着他把手臂竖直举起,测得影子长为1.1m,那么小刚举起的手臂超出头顶( )
A.0.5m
B.0.55m
C.0.6m
D.2.2m
4.如图,是斜靠在墙壁上的长梯,梯脚距离墙角,梯上点距离墙,长,则梯子长为(
)
A.
B.
C.
D.
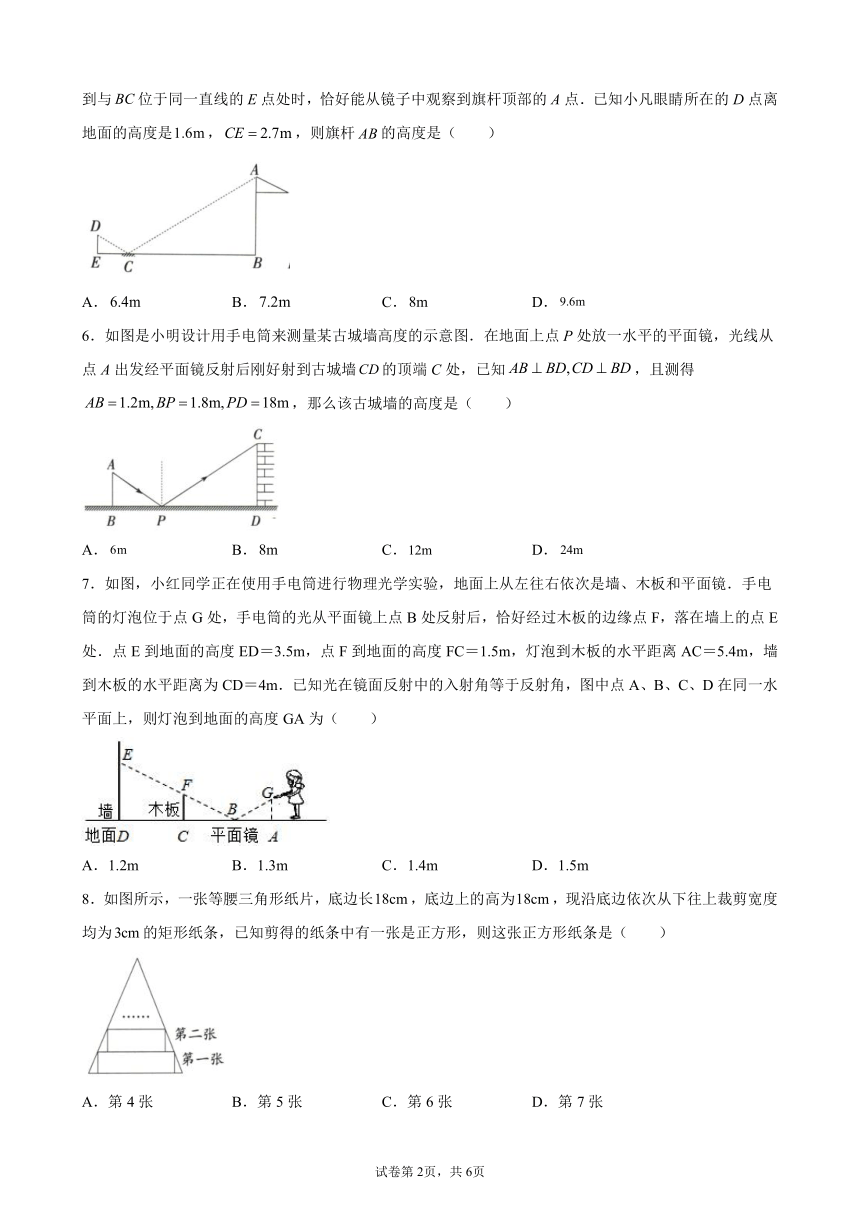
5.如图,为了测量旗杆的高度,小凡在距旗杆底部B点的C点处放置了一面镜子,当小凡行走到与位于同一直线的E点处时,恰好能从镜子中观察到旗杆顶部的A点.已知小凡眼睛所在的D点离地面的高度是,,则旗杆的高度是(
)
A.
B.
C.
D.
6.如图是小明设计用手电筒来测量某古城墙高度的示意图.在地面上点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙的顶端C处,已知,且测得,那么该古城墙的高度是(
)
A.
B.
C.
D.
7.如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡位于点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度ED=3.5m,点F到地面的高度FC=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上,则灯泡到地面的高度GA为( )
A.1.2m
B.1.3m
C.1.4m
D.1.5m
8.如图所示,一张等腰三角形纸片,底边长,底边上的高为,现沿底边依次从下往上裁剪宽度均为的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是(
)
A.第4张
B.第5张
C.第6张
D.第7张
二、填空题
9.一把剪刀如图所示,
,当手握的地方张开时,剪刀的尖端,两点的距离为________
10.如图,小明在路灯下,向前走5米到处,发现自己在地面上的影子长是2米.若小明的身高是1.8米,则路灯离地面的高度是________米.
11.在同一时刻,小红测得小亮的影长为,教学楼的影长为,已知小亮的身高为,那么教学楼的高度为________m.
12.一个米高的人,站在距离路灯杆米的地方,他在人行道上的影子是米长,则路灯杆的高度是________米.
13.如图,要测量、两点间距离,在点打桩,使是中点,使也是中点,测得米,则________米.
14.如图,有点光源在平面镜上面,若在点看到点光源的反射光线,并测得,,,且,则点光源到平面镜的距离的长度为________.
15.如图,电线杆上的路灯距离地面,身高的小明()站在距离电线杆的底部(点O)的A处,则小明的影子长为________m.
16.如图,有一个广告牌OE,小明站在距广告牌OE10米远的A处观察广告牌顶端,眼睛距地面1.5米,他的前方5米处有一堵墙DC,若墙高DC=2米,则广告牌OE的高度为______米.
三、解答题
17.在△ABC中,AB=8,点D、E分别在边AB、AC上,且DE∥BC,若DE把△ABC分成了面积相等的两部分,求BD的长.
18.在相同时刻的物高与影长成正比例,如果在某时,旗杆在地面上的影长为10米,此时身高是米的小明的影长是米,求旗杆的高度.
19.小玲用下面的方法来测量学校教学大楼的高度.在水平地面上放一面平面镜,镜子与教学大楼的距离米.当她与镜子的距离米时,她刚好能从镜子中看到教学大楼的顶端.已知她的眼睛距地面高度米,请你帮助小玲计算出教学大楼的高度是多少米.(注意:根据光的反射定律:反射角等于入射角)
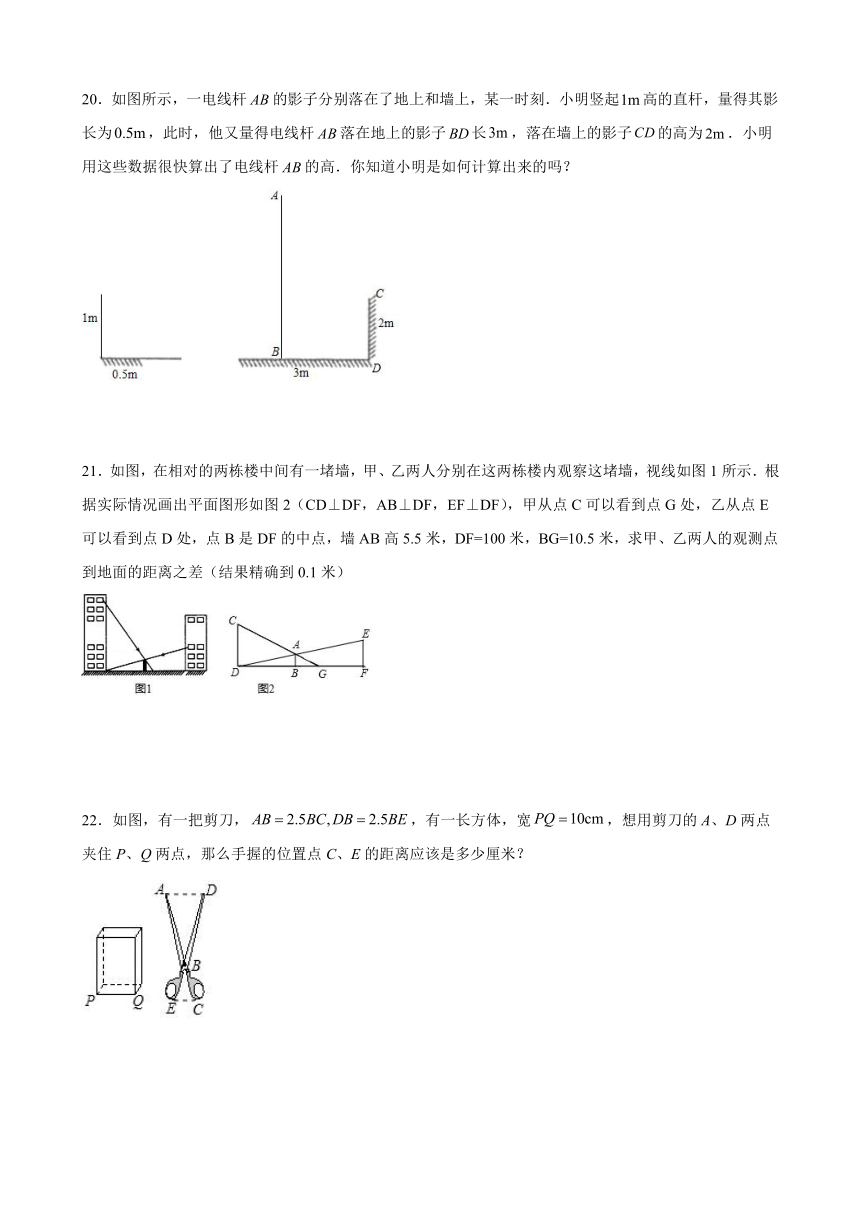
20.如图所示,一电线杆的影子分别落在了地上和墙上,某一时刻.小明竖起高的直杆,量得其影长为,此时,他又量得电线杆落在地上的影子长,落在墙上的影子的高为.小明用这些数据很快算出了电线杆的高.你知道小明是如何计算出来的吗?
21.如图,在相对的两栋楼中间有一堵墙,甲、乙两人分别在这两栋楼内观察这堵墙,视线如图1所示.根据实际情况画出平面图形如图2(CD⊥DF,AB⊥DF,EF⊥DF),甲从点C可以看到点G处,乙从点E可以看到点D处,点B是DF的中点,墙AB高5.5米,DF=100米,BG=10.5米,求甲、乙两人的观测点到地面的距离之差(结果精确到0.1米)
22.如图,有一把剪刀,,有一长方体,宽,想用剪刀的A、D两点夹住P、Q两点,那么手握的位置点C、E的距离应该是多少厘米?
23.如图,一条东西走向的笔直公路,点A、B表示公路北侧间隔150米的两棵树所在的位置,点C表示电视塔所在的位置.小王在公路PQ南侧直线行走,当他到达点P的位置时,观察树A恰好挡住电视塔,即点P、A、C在一条直线上,当他继续走180米到达点Q的位置时,以同样方法观察电视塔,观察树B也恰好挡住电视塔.假设公路两侧AB∥PQ,且公路的宽为60米,求电视塔C到公路南侧PQ的距离.
24.如图,王华同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行12
m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部.已知王华同学的身高是1.6
m,两个路灯的高度都是9.6
m
(1)求两个路灯之间的距离;
(2)当王华同学走到路灯BD处时,他在路灯AC下的影子长是多少?
试卷第1页,共3页
参考答案
1.C
【解析】解:∵AB⊥BF,ED⊥BF,
∴AB∥DE,
∴△ABC∽△EDC,
∴,
即,
解得:AB=40,
故选:C.
2.D
【解析】解:米长的标杆测得其影长为米,即某一时刻实际高度和影长之比为定值,
所以墙上的米投射到地面上实际为米,即旗杆影长为米,
因此旗杆总高度为米,
故选.
3.A
【解析】根据在同一时刻,物体的实际高度和影长成比例,
设小刚举起的手臂超出头顶是xm,则有,
解得:x=0.5.
故选:A
4.C
【解析】解:如图,由题意设DE⊥AC于E点,BC⊥AC于C点,
则,,
∵DE⊥AC,BC⊥AC,
∴DE∥BC,
∴△ADE∽△ABC,
∴,
设,
则,
解得:,
经检验,是上述分式方程的解,
∴,
故选:C.
5.A
【解析】解:过点C作镜面的法线CH,由光学原理得∠DCH=∠ACH,
∵∠DCE=90°-∠DCH,
∠ACB=90°-∠ACH,
∴∠DCE=∠ACB,
又∵∠DEC=∠ABC=90°,
∴△CDE∽△CAB,
∴,即,
解得AB=6.4(m).
答:旗杆AB高为6.4米.
故选A.
6.C
【解析】由题意知:,
∴
∴
∵,,
∴
∴
故选:C
7.A
【解析】解:由题意可得:FC∥DE,
∴△BFC∽BED,
∴,即,解得:BC=3m,
则AB=5.4-3=2.4m,
∵光在镜面反射中的入射角等于反射角,
∴∠FBC=∠GBA,
∵∠FCB=∠GAB,
∴△BGA∽△BFC,
∴,即,解得AG=1.2m.
故选:A.
8.B
【解析】解:已知剪得的纸条中有一张是正方形,则该正方形的边长为,
设从顶点到这个正方形顶边的距离为,
根据相似三角形的性质可得,解得(张),
所以这张正方形纸条是第5张,
故选B.
9.6
【解析】解:,且,
∴,
,
解得:.
故答案为:.
10.6.3
【解析】解:由图知,DC=2米,ED=1.8米,AD=5米,
∴AC=AD+DC=5+2=7米
∵ED∥AB,
∴△ECD∽△BCA
∴
即
∴(米).
故答案为:6.3
11.18
【解析】解:设教学楼的高度为,
∵小亮的影长为,教学楼的影长为,小亮的身高为,
∴,解得,
即教学楼的高度为.
故答案为:18.
12.5.4
【解析】解:如图所示,设路灯杆的高度是米,
米,米,米,
∵
,,
∴
,
∴
,
即,
解得米.
故答案为:.
13.31.4
【解析】解:∵O是AC中点,O也是BD中点,
∴BO=OD,AO=OC,
∴,
又∵∠BOA=∠DOC,
∴,
∴,
∴米,
故答案为:31.4.
14.12
【解析】解:由题意得∠ABS=∠CBP,∠SAB=∠PCB=90°,
∴△ABS∽△CBP,
∴,
即,
解得:,
故答案为:12.
15.5
【解析】解:如图,由题意得,AB∥OC
∴
∴,
,
解得.
故答案为5.
16.2.5
【解析】解:如图,作BF⊥OE于点F,交CD于点G,
根据题意得:AB=CG=OF=1.5米,BF=10米,BG=5米,DG=CD-CG=2-1.5=0.5米,
∵DG∥EF,
∴∠BGD=∠BFE,∠BDG=∠BEF,
∴∽,
∴,
∴,
解得:EF=1,
∴EO=EF+OF=1+1.5=2.5(米).
故答案为:2.5.
17.BD=
【解析】解:∵DE∥BC
∴△ADE∽△ABC
∵△ADE与△ABC的面积的比等于1:2
∴AD:AB=
∵AB=8
∴AD=
∴BD=
18.12米
【解析】解:设此时高为x米的旗杆的影长为10m,
根据题意得,
解得x=12.
所以此时高为12米的旗杆的影长为10m.
19.13.44米
【解析】解:根据题意可得:
,,
∴,
∴,
∴,
∴(米)
∴教学大楼的高度是米.
20.8m,见解析
【解析】解:过点C作CEBD,交AB于点E,则四边形CEBD为矩形.
∴CE=BD=3,EB=CD=2,
依题意有,即,
∴AE=6,
∴AB=AE+EB=6+2=8.
即电线杆AB的高为8米,
故答案为:8米.
21.甲、乙两人的观测点到地面的距离之差约为20.7米.
【解析】解:由题意得∠ABG=∠CDG=90°,
又∵∠AGD为公共角,
∴△ABG∽△CDG,
∴=,
∵AB=5.5米,BG=10.5米,
∴=,
∴CD≈31.69(米)
又∵∠ABD=∠EFD=90°,∠EDF为公共角,
∴△ADB∽△EDF,
∴==,
∴EF=2AB=11(米)
∴CD-EF≈20.7(米)
答:甲、乙两人的观测点到地面的距离之差约为20.7米.
22.
【解析】解:∵,
∴,
又∵,
∴,
∴,
即,
解得.
所以,点C、E的距离应该是4厘米.
23.电视塔C到公路南侧所在直线PQ的距离是360米.
【解析】如图所示,作CE⊥PQ于E,交AB于D点,
设CD为x,则CE=60+x,
∵AB∥PQ,
∴△ABC∽△PQC,
∴=,即=,
解得x=300,
∴x+60=360米,
答:电视塔C到公路南侧所在直线PQ的距离是360米.
24.(1)18;(2)3.6
【解析】解:(1)由对称性可知AP=BQ,设AP=BQ=x
m,
∵MP∥BD,
∴△APM∽△ABD,
∴
,
∴=,
解得x=3,
∴AB=2x+12=18(m),即两个路灯之间的距离为18米
(2)设王华走到路灯BD处头的顶部为E,连接CE并延长交AB的延长线于点F,则BF即为此时他在路灯AC下的影子长,
设BF=y
m,
∵BE∥AC,
∴△FEB∽△FCA,
∴
,即=,
解得y=3.6,
当王华同学走到路灯BD处时,他在路灯AC下的影子长3.6米.
答案第1页,共2页
答案第1页,共2页
23.3.4相似三角形的应用-同步练习
时间:60分钟
一、单选题
1.如图,A,B两点被一河隔开,为了测量A,B两点间的距离,小明过点B作BF⊥AB,在BF上取两点C,D,使BC=2CD,过点D作DE⊥BF且使点A,C,E在同一条直线上,测得DE=20m,则A,B两点间的距离是(
)
A.60m
B.50m
C.40m
D.30m
2.某同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立米长的标杆测得其影厂为米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为米和米,则学校旗杆的高度为(
)米.
A.
B.
C.
D.
3.小刚身高1.7m,测得他站立在阳光下的影子长为0.85m,紧接着他把手臂竖直举起,测得影子长为1.1m,那么小刚举起的手臂超出头顶( )
A.0.5m
B.0.55m
C.0.6m
D.2.2m
4.如图,是斜靠在墙壁上的长梯,梯脚距离墙角,梯上点距离墙,长,则梯子长为(
)
A.
B.
C.
D.
5.如图,为了测量旗杆的高度,小凡在距旗杆底部B点的C点处放置了一面镜子,当小凡行走到与位于同一直线的E点处时,恰好能从镜子中观察到旗杆顶部的A点.已知小凡眼睛所在的D点离地面的高度是,,则旗杆的高度是(
)
A.
B.
C.
D.
6.如图是小明设计用手电筒来测量某古城墙高度的示意图.在地面上点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙的顶端C处,已知,且测得,那么该古城墙的高度是(
)
A.
B.
C.
D.
7.如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡位于点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度ED=3.5m,点F到地面的高度FC=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上,则灯泡到地面的高度GA为( )
A.1.2m
B.1.3m
C.1.4m
D.1.5m
8.如图所示,一张等腰三角形纸片,底边长,底边上的高为,现沿底边依次从下往上裁剪宽度均为的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是(
)
A.第4张
B.第5张
C.第6张
D.第7张
二、填空题
9.一把剪刀如图所示,
,当手握的地方张开时,剪刀的尖端,两点的距离为________
10.如图,小明在路灯下,向前走5米到处,发现自己在地面上的影子长是2米.若小明的身高是1.8米,则路灯离地面的高度是________米.
11.在同一时刻,小红测得小亮的影长为,教学楼的影长为,已知小亮的身高为,那么教学楼的高度为________m.
12.一个米高的人,站在距离路灯杆米的地方,他在人行道上的影子是米长,则路灯杆的高度是________米.
13.如图,要测量、两点间距离,在点打桩,使是中点,使也是中点,测得米,则________米.
14.如图,有点光源在平面镜上面,若在点看到点光源的反射光线,并测得,,,且,则点光源到平面镜的距离的长度为________.
15.如图,电线杆上的路灯距离地面,身高的小明()站在距离电线杆的底部(点O)的A处,则小明的影子长为________m.
16.如图,有一个广告牌OE,小明站在距广告牌OE10米远的A处观察广告牌顶端,眼睛距地面1.5米,他的前方5米处有一堵墙DC,若墙高DC=2米,则广告牌OE的高度为______米.
三、解答题
17.在△ABC中,AB=8,点D、E分别在边AB、AC上,且DE∥BC,若DE把△ABC分成了面积相等的两部分,求BD的长.
18.在相同时刻的物高与影长成正比例,如果在某时,旗杆在地面上的影长为10米,此时身高是米的小明的影长是米,求旗杆的高度.
19.小玲用下面的方法来测量学校教学大楼的高度.在水平地面上放一面平面镜,镜子与教学大楼的距离米.当她与镜子的距离米时,她刚好能从镜子中看到教学大楼的顶端.已知她的眼睛距地面高度米,请你帮助小玲计算出教学大楼的高度是多少米.(注意:根据光的反射定律:反射角等于入射角)
20.如图所示,一电线杆的影子分别落在了地上和墙上,某一时刻.小明竖起高的直杆,量得其影长为,此时,他又量得电线杆落在地上的影子长,落在墙上的影子的高为.小明用这些数据很快算出了电线杆的高.你知道小明是如何计算出来的吗?
21.如图,在相对的两栋楼中间有一堵墙,甲、乙两人分别在这两栋楼内观察这堵墙,视线如图1所示.根据实际情况画出平面图形如图2(CD⊥DF,AB⊥DF,EF⊥DF),甲从点C可以看到点G处,乙从点E可以看到点D处,点B是DF的中点,墙AB高5.5米,DF=100米,BG=10.5米,求甲、乙两人的观测点到地面的距离之差(结果精确到0.1米)
22.如图,有一把剪刀,,有一长方体,宽,想用剪刀的A、D两点夹住P、Q两点,那么手握的位置点C、E的距离应该是多少厘米?
23.如图,一条东西走向的笔直公路,点A、B表示公路北侧间隔150米的两棵树所在的位置,点C表示电视塔所在的位置.小王在公路PQ南侧直线行走,当他到达点P的位置时,观察树A恰好挡住电视塔,即点P、A、C在一条直线上,当他继续走180米到达点Q的位置时,以同样方法观察电视塔,观察树B也恰好挡住电视塔.假设公路两侧AB∥PQ,且公路的宽为60米,求电视塔C到公路南侧PQ的距离.
24.如图,王华同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行12
m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部.已知王华同学的身高是1.6
m,两个路灯的高度都是9.6
m
(1)求两个路灯之间的距离;
(2)当王华同学走到路灯BD处时,他在路灯AC下的影子长是多少?
试卷第1页,共3页
参考答案
1.C
【解析】解:∵AB⊥BF,ED⊥BF,
∴AB∥DE,
∴△ABC∽△EDC,
∴,
即,
解得:AB=40,
故选:C.
2.D
【解析】解:米长的标杆测得其影长为米,即某一时刻实际高度和影长之比为定值,
所以墙上的米投射到地面上实际为米,即旗杆影长为米,
因此旗杆总高度为米,
故选.
3.A
【解析】根据在同一时刻,物体的实际高度和影长成比例,
设小刚举起的手臂超出头顶是xm,则有,
解得:x=0.5.
故选:A
4.C
【解析】解:如图,由题意设DE⊥AC于E点,BC⊥AC于C点,
则,,
∵DE⊥AC,BC⊥AC,
∴DE∥BC,
∴△ADE∽△ABC,
∴,
设,
则,
解得:,
经检验,是上述分式方程的解,
∴,
故选:C.
5.A
【解析】解:过点C作镜面的法线CH,由光学原理得∠DCH=∠ACH,
∵∠DCE=90°-∠DCH,
∠ACB=90°-∠ACH,
∴∠DCE=∠ACB,
又∵∠DEC=∠ABC=90°,
∴△CDE∽△CAB,
∴,即,
解得AB=6.4(m).
答:旗杆AB高为6.4米.
故选A.
6.C
【解析】由题意知:,
∴
∴
∵,,
∴
∴
故选:C
7.A
【解析】解:由题意可得:FC∥DE,
∴△BFC∽BED,
∴,即,解得:BC=3m,
则AB=5.4-3=2.4m,
∵光在镜面反射中的入射角等于反射角,
∴∠FBC=∠GBA,
∵∠FCB=∠GAB,
∴△BGA∽△BFC,
∴,即,解得AG=1.2m.
故选:A.
8.B
【解析】解:已知剪得的纸条中有一张是正方形,则该正方形的边长为,
设从顶点到这个正方形顶边的距离为,
根据相似三角形的性质可得,解得(张),
所以这张正方形纸条是第5张,
故选B.
9.6
【解析】解:,且,
∴,
,
解得:.
故答案为:.
10.6.3
【解析】解:由图知,DC=2米,ED=1.8米,AD=5米,
∴AC=AD+DC=5+2=7米
∵ED∥AB,
∴△ECD∽△BCA
∴
即
∴(米).
故答案为:6.3
11.18
【解析】解:设教学楼的高度为,
∵小亮的影长为,教学楼的影长为,小亮的身高为,
∴,解得,
即教学楼的高度为.
故答案为:18.
12.5.4
【解析】解:如图所示,设路灯杆的高度是米,
米,米,米,
∵
,,
∴
,
∴
,
即,
解得米.
故答案为:.
13.31.4
【解析】解:∵O是AC中点,O也是BD中点,
∴BO=OD,AO=OC,
∴,
又∵∠BOA=∠DOC,
∴,
∴,
∴米,
故答案为:31.4.
14.12
【解析】解:由题意得∠ABS=∠CBP,∠SAB=∠PCB=90°,
∴△ABS∽△CBP,
∴,
即,
解得:,
故答案为:12.
15.5
【解析】解:如图,由题意得,AB∥OC
∴
∴,
,
解得.
故答案为5.
16.2.5
【解析】解:如图,作BF⊥OE于点F,交CD于点G,
根据题意得:AB=CG=OF=1.5米,BF=10米,BG=5米,DG=CD-CG=2-1.5=0.5米,
∵DG∥EF,
∴∠BGD=∠BFE,∠BDG=∠BEF,
∴∽,
∴,
∴,
解得:EF=1,
∴EO=EF+OF=1+1.5=2.5(米).
故答案为:2.5.
17.BD=
【解析】解:∵DE∥BC
∴△ADE∽△ABC
∵△ADE与△ABC的面积的比等于1:2
∴AD:AB=
∵AB=8
∴AD=
∴BD=
18.12米
【解析】解:设此时高为x米的旗杆的影长为10m,
根据题意得,
解得x=12.
所以此时高为12米的旗杆的影长为10m.
19.13.44米
【解析】解:根据题意可得:
,,
∴,
∴,
∴,
∴(米)
∴教学大楼的高度是米.
20.8m,见解析
【解析】解:过点C作CEBD,交AB于点E,则四边形CEBD为矩形.
∴CE=BD=3,EB=CD=2,
依题意有,即,
∴AE=6,
∴AB=AE+EB=6+2=8.
即电线杆AB的高为8米,
故答案为:8米.
21.甲、乙两人的观测点到地面的距离之差约为20.7米.
【解析】解:由题意得∠ABG=∠CDG=90°,
又∵∠AGD为公共角,
∴△ABG∽△CDG,
∴=,
∵AB=5.5米,BG=10.5米,
∴=,
∴CD≈31.69(米)
又∵∠ABD=∠EFD=90°,∠EDF为公共角,
∴△ADB∽△EDF,
∴==,
∴EF=2AB=11(米)
∴CD-EF≈20.7(米)
答:甲、乙两人的观测点到地面的距离之差约为20.7米.
22.
【解析】解:∵,
∴,
又∵,
∴,
∴,
即,
解得.
所以,点C、E的距离应该是4厘米.
23.电视塔C到公路南侧所在直线PQ的距离是360米.
【解析】如图所示,作CE⊥PQ于E,交AB于D点,
设CD为x,则CE=60+x,
∵AB∥PQ,
∴△ABC∽△PQC,
∴=,即=,
解得x=300,
∴x+60=360米,
答:电视塔C到公路南侧所在直线PQ的距离是360米.
24.(1)18;(2)3.6
【解析】解:(1)由对称性可知AP=BQ,设AP=BQ=x
m,
∵MP∥BD,
∴△APM∽△ABD,
∴
,
∴=,
解得x=3,
∴AB=2x+12=18(m),即两个路灯之间的距离为18米
(2)设王华走到路灯BD处头的顶部为E,连接CE并延长交AB的延长线于点F,则BF即为此时他在路灯AC下的影子长,
设BF=y
m,
∵BE∥AC,
∴△FEB∽△FCA,
∴
,即=,
解得y=3.6,
当王华同学走到路灯BD处时,他在路灯AC下的影子长3.6米.
答案第1页,共2页
答案第1页,共2页
