2021-2022学年人教版五年级数学上册《6.3 梯形的面积》同步练习(含答案)
文档属性
| 名称 | 2021-2022学年人教版五年级数学上册《6.3 梯形的面积》同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 159.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 15:13:29 | ||
图片预览




文档简介
2021-2022学年人教版五年级数学上册《6.3
梯形的面积》同步练习
一、填空题
1.梯形上底是5cm,下底是10cm,面积是30平方厘米,高是
cm。
2.有一个梯形的面积是48dm2,它的上底和下底的平均长度是24dm,这个梯形的高是
dm。
3.一个直角梯形的上底长5分米,下底长8分米,两条腰分别是4分米和5分米,这个直角梯形面积是
平方分米。
4.一堆钢管,已知最上层7根,最下层有19根,相邻两层之间相差1根,这堆钢管共有
根。
5.妈妈的手提包侧面的形状是个梯形,上底是18cm,下底是22cm,高是15cm,面积是
cm2。
6.一个梯形果园,上底是300米,下底是500米,高是100米。这个果园的面积等于
公顷。
二、单选题
7.一个梯形的上底增加10厘米,下底减少10厘米,高不变,梯形现在的面积( )
A.增加10平方厘米
B.减少10平方厘米
C.不变
D.无法确定
8.在图中,平行线间的三个图形,它们的面积相比( )
A.平行四边形的面积大
B.三角形的面积大
C.梯形的面积大
D.面积都相等
9.梯形的上底是8米,下底是3米,高是下底的2倍,这个梯形的面积是( )
A.22平方米
B.33平方米
C.66平方米
10.一个梯形的上底长36dm,如果补上一块底为64dm,面积为64dm2的三角形,就变成了一个平行四边形,这个梯形的面积是( )
A.20dm2
B.136dm2
C.272dm2
D.68dm2
11.一个梯形的面积是24平方米,高是8米,它的上、下底的和是( )
A.3米
B.4米
C.6米
D.8米
12.梯形的上底扩大到原来的3倍,下底也扩大到原来的3倍,高不变,那么它的面积( )
A.扩大到原来的3倍
B.扩大到原来的9倍
C.扩大到原来的6倍
D.不变
三、判断题
13.两个面积相等的梯形,形状和大小也一定相同。
(判断对错)
14.梯形的上底下底越长,面积越大.
.(判断对错)
15.梯形的面积等于平行四边形面积的一半.
.(判断对错)
16.一个梯形的上底、下底和高都扩大到它的2倍,那么面积扩大到原来的4倍.
(判断对错)
17.一个梯形上、下底的和是6dm,高是10dm,它的面积是30dm2.
(判断对错)
18.一个梯形的上底是6米,下底是8米,面积是42平方米,它的高是6米.
(判断对错)
四、计算题
19.计算图形的面积。
(1);
(2)。
20.计算图形的面积。(单位:厘米))
五、作图题
21.按要求在方格图中画图。
(1)画一个平行四边形,使它的面积与图中长方形的面积相等;
(2)画一个三角形,使它的面积是图中长方形的面积的一半;
(3)画一个梯形,使它的面积是图中长方形的面积的2倍。
22.按要求在格子图中画图(每个小方格表示1平方厘米)。
(1)画一个与已知平行四边形面积相等,底也相等三角形;
(2)以AB为下底,画一个面积为9平方厘米的梯形。
六、解决问题
23.爷爷在一块上底是120m,下底是180m,高是60m的梯形果园种果树,如果每棵果树占地面积10m2,这个果园一共可以种多少棵果树?
24.一块菜地一面靠墙,用62米的篱笆刚好把菜地的三条边围起来(如图),这块菜地的面积是多少平方米?
25.小冬家用50m长的竹篱笆,靠墙边围成了一块瓜地(见图).如果平均每平方米地可以栽种4棵瓜苗,这块地可以栽种多少棵瓜苗?
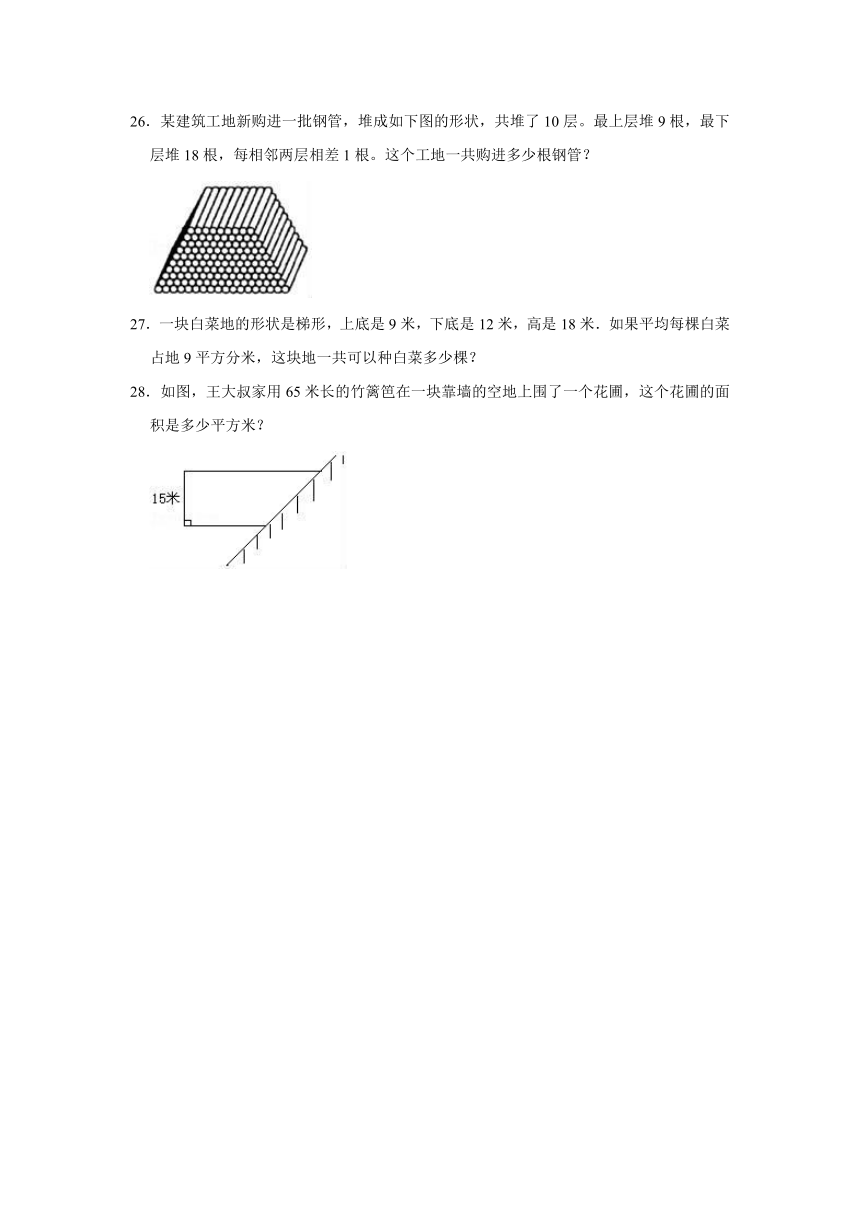
26.某建筑工地新购进一批钢管,堆成如下图的形状,共堆了10层。最上层堆9根,最下层堆18根,每相邻两层相差1根。这个工地一共购进多少根钢管?
27.一块白菜地的形状是梯形,上底是9米,下底是12米,高是18米.如果平均每棵白菜占地9平方分米,这块地一共可以种白菜多少棵?
28.如图,王大叔家用65米长的竹篱笆在一块靠墙的空地上围了一个花圃,这个花圃的面积是多少平方米?
参考答案与试题解析
一、填空题
1.【分析】根据梯形的面积公式:S=(a+b)h÷2,那么h=2S÷(a+b),把数据代入公式解答。
【解答】解:30×2÷(5+10)
=60÷15
=4(厘米)
答:高是4厘米。
故答案为:4。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
2.【分析】根据梯形的面积公式:S=(a+b)h÷2,那么h=2S÷(a+b),把数据代入公式解答。
【解答】解:48×2÷(24×2)
=96÷48
=2(分米)
答:这个梯形的高是2分米。
故答案为:2。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
3.【分析】根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【解答】解:(5+8)×4÷2
=13×4÷2
=26(平方分米)
答:这个直角梯形面积是26平方分米。
故答案为:26。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
4.【分析】已知最上层7根,最下层有19根,相邻两层之间相差1根,首先求出层数(高),层数=最下层的根数﹣最上层根数+1,根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【解答】解:(7+19)×(19﹣7+1)÷2
=26×13÷2
=169(根)
答:这堆钢管共有169根。
故答案为:169。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
5.【分析】根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【解答】解:(18+22)×15÷2
=40×15÷2
=300(平方厘米)
答:面积是300平方厘米。
故答案为:300。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
6.【分析】根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【解答】解:(300+500)×100÷2
=800×100÷2
=40000(平方米)
40000平方米=4公顷
答:这个果园的面积是4公顷。
故答案为:4。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
二、单选题
7.【分析】根据梯形的面积公式:S=(a+b)h÷2,一个梯形的上底增加10厘米,下底减少10厘米,高不变,也就是梯形上下底之和不变,所以梯形现在的面积与原来的面积相等。据此解答。
【解答】解:一个梯形的上底增加10厘米,下底减少10厘米,高不变,也就是梯形上下底之和不变,所以梯形现在的面积与原来的面积相等。
答:梯形现在的面积不变。
故选:C。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
8.【分析】在图中,三个图形的高相等,梯形的上底、下底、平行四边形的底、三角形的底都已知,再依据三者的面积公式即可判断它们的面积大小.
【解答】解:设高为h,
平行四边形的面积=4h=4h
三角形的面积=×8×h=4h
梯形面积=(2+6)×h÷2=4h
所以它们的面积相比,都相等;
故选:D。
【点评】此题主要考查等高的平行四边形、三角形和梯形的面积大小比较,将数据代入各自的面积公式即可求解.
9.【分析】高是下底的2倍,所以高是3×2=6米,根据梯形的面积=(上底+下底)×高÷2,代入数据计算即可解答.
【解答】解:(8+3)×3×2÷2
=11×6÷2
=33(平方米)
答:这个图形的面积是33平方米.
故选:B。
【点评】此题考查了梯形的面积公式的计算应用.
10.【分析】由“如果补上一块底为64dm,面积为64dm2的三角形,就变成了一个平行四边形”可得:平行四边形的底为(36+64)分米,利用三角形的面积公式即可求出三角形的高,也就是梯形的高,于是就可以利用梯形的面积公式求解.
【解答】解:64×2÷64=2(分米),
36+64=100(分米),
(36+100)×2÷2
=136×2÷2
=136(平方分米).
答:这个梯形的面积是136平方分米.
故选:B。
【点评】此题主要考查了三角形和梯形的面积的计算方法,关键是由题目条件先求出:梯形的下底和高的值.
11.【分析】根据梯形的面积公式:S=(a+b)h÷2,那么a+b=2S÷h,把数据代入公式解答。
【解答】解:24×2÷8
=48÷8
=6(米)
答:它的上、下底的和是6米。
故选:C。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
12.【分析】根据题意可知,梯形的上底和下底都扩大到原来的3倍,也就是说(上底+下底)的和扩大到原来的3倍,高不变,它的面积一定也扩大到原来的3倍。
【解答】解:设上底为a,下底为b,高为h,
原来的面积是:S=(a+b)×h÷2;
扩大后的面积是:
(a×3+b×3)×h÷2
=(a+b)×3×h÷2
=[(a+b)×h÷2]×3;
所以梯形的上底和下底都扩大到原来的3倍,高不变,它的面积也随之扩大到原来的3倍。
故选:A。
【点评】本题用到的知识点是:S=(a+b)×h÷2;两个加数都扩大几倍,它们的和也扩大几倍。
三、判断题
13.【分析】因为梯形的面积S=(a+b)×h÷2,即梯形的面积只与上底、下底和高的长度有关,而与梯形的形状无关,据此求解即可。
【解答】解:梯形的面积只与上底、下底和高的长度有关,而与梯形的形状无关,所以“两个面积相等的梯形,形状和大小也一定相同”的说法是错误的。
故答案为:×。
【点评】解决本题的关键在于知道梯形的面积只与上底、下底和高的长度有关。
14.【分析】根据梯形的面积公式=(上底+下底)×高÷2可知,梯形的面积由上底、下底、高的大小决定,如果梯形的上底、下底越长,而梯形的高最小,则梯形的面积不是最大,据此解答即可.
【解答】解:根据梯形的面积公式,梯形的面积由上底、下底、高三个要素确定,上底和下底越长不能说它们的面积就越大.
故判:×.
【点评】此题主要考查的是梯形面积公式的灵活应用.
15.【分析】缺少关键条件,梯形的面积是和它等底等高的平行四边形面积的一半.
【解答】解:因为梯形的面积是和它等底等高的平行四边形面积的一半.
故答案为:×.
【点评】此题主要考查梯形的面积是和它等底等高的平行四边形面积的一半.
16.【分析】依据梯形的面积=(a+b)×h÷2,若“梯形的上底、下底和高都扩大到它的2倍”,则梯形的上底为2a,下底为2b,高为2h,分别求出扩大前后梯形的面积,用扩大后的面积除以扩大前的面积即得扩大的倍数.
【解答】解:原梯形的面积为(a+b)×h÷2,
扩大后的面积为:(2a+2b)×2h÷2
=4[(a+b)×h÷2]
4[(a+b)×h÷2]÷[(a+b)×h÷2]=4倍,
所以一个梯形的上底、下底、高分别扩大2倍,它的面积扩大4倍.
所以题干说法正确.
故答案为:√.
【点评】此题主要考查梯形的面积公式的灵活运用.
17.【分析】根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式求出它的面积,然后与30平方分米进行比较即可.
【解答】解:6×10÷2
=60÷2
=30(平方分米)
答:它的面积是30平方分米.
故答案为:√.
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式.
18.【分析】根据梯形的面积公式:S=(a+b)h÷2,那么h=2S÷(+b),据此求出梯形的高,然后与6米进行比较。
【解答】解:42×2÷(6+8)
=84÷14
=6(米)
6=6
因此,题干中的计算是正确的。
故答案为:√。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
四、计算题
19.【分析】(1)根据梯形面积=(上底+下底)×高÷2,代入数据求解即可;
(2)该图形的面积=长方形的面积﹣三角形的面积,根据长方形面积=长×宽,三角形面积=底×高÷2,代入数据求解即可。
【解答】解:(1)(2.6+3.4)×5.2÷2
=6×5.2÷2
=31.2÷2
=15.6(平方米)
答:该图形的面积是15.6平方米。
(2)40×30﹣30×10÷2
=1200﹣150
=1050(平方厘米)
答:该图形的面积是1050平方厘米。
【点评】本题主要考查求解梯形面积和组合图形面积的方法。注意求组合图形面积时要将不规则图形转化为规则图形的面积差来求解。
20.【分析】根据梯形面积=(上底+下底)×高÷2,代入数据求解即可。
【解答】解:(6+8)×5÷2
=14×5÷2
=35(平方厘米)
答:该图形的面积是35平方厘米。
【点评】本题主要考查梯形面积公式的应用,解决本题的关键在于分清梯形的各部分名称。
五、作图题
21.【分析】(1)当平行四边形的底等于长方形的长,平行四边形的高等于长方形的宽时,它们的面积相等。据此画图。
(2)根据三角形的面积:S=ah÷2,要画一个三角形,使它的面积是图中长方形的面积的一半,这个三角形的底等于长方形的长,三角形的高等于长方形的宽。据此画图。
(3)根据梯形的面积公式:S=(a+b)h÷2,要使梯形的面积等于图中长方形的2倍,画法不唯一,可以画一个高是3厘米,上底是3厘米,下底是5厘米的图形。据此解答。
【解答】解:(1)画法不唯一。画图如下:
(2)画法不唯一。画图如下:
(3)画法不唯一。画图如下:
【点评】此题考查的目的是理解掌握平行四边形、三角形、梯形的特征,以及平行四边形、三角形、梯形的面积公式及应用。
22.【分析】(1)因为等底等高的三角形的面积是平行四边形面积的一半,要使三角形的面积等于平行四边形的面积,三角形的底等于平行四边形的底,那么三角形的高是平行四边形高的2倍。据此画图。
(2)根据梯形的面积公式:S=(a+b)h÷2,画法不唯一,可以画一个上底是4厘米,高是2厘米的梯形。
【解答】解:(1)画法不唯一。画图如下:
(2)画法不唯一。画图如下:
【点评】此题主要考查平行四边形、三角形、梯形面积公式的灵活运用,关键是熟记公式。
六、解决问题
23.【分析】根据梯形的面积公式:S=(a+b)h÷2,求出这块地的面积,然后根据“包含”除法的意义,用这块地面积除以每棵果树的占地面积即可。
【解答】解:(120+180)×60÷2÷10
=300×60÷2÷10
=9000÷10
=900(棵)
答:这个果园一共可以种果树900棵。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
24.【分析】用三条边的长度和42米减去高就是梯形上下底的和,然后再根据梯形面积=(上底+下底)×高÷2解答即可。
【解答】解:菜地为梯形:上底与下底的和:62﹣26=36(米),
36×26÷2=468(平方米)
答:这块菜地的面积是468平方米。
【点评】本题主要是利用梯形的面积公式S=(a+b)×h÷2解决问题。
25.【分析】用50m长的竹篱笆,靠墙边围成了一块瓜地,那么用50减去20就是围成的梯形上底与下底的和;根据梯形的面积公式求出梯形的面积,再乘平均每平方米栽种瓜苗的棵数,就是这块地可以栽种多少棵瓜苗.
【解答】解:(50﹣20)×20÷2×4
=30×40
=1200(棵)
答:这块地可以栽种1200棵瓜苗.
【点评】本题的主要考查了学生根据梯形的面积公式S=(a+b)×h÷2解答问题的能力.
26.【分析】根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【解答】解:(9+18)×10÷2
=27×10÷2
=135(根)
答:这个工地一共购进135根钢管。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
27.【分析】根据梯形的面积=(上底+下底)×高÷2,求出这块地的面积,再求出这个面积里面有几个9平方分米,即可求出一共有几棵白菜,据此计算即可解答.
【解答】解:9平方分米=0.09平方米
(9+12)×18÷2÷0.09
=21×18÷2÷0.09
=189÷0.09
=2100(棵)
答:这块地一共可以种白菜2100棵.
【点评】此题考查了梯形的面积公式的计算应用.
28.【分析】通过观察图形可知,一面靠墙,用65米长的篱笆围成一个直角梯形,梯形的高是15米,那么梯形上底、下底之和是(65﹣15)米,根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【解答】解:(65﹣15)×15÷2
=50×15÷2
=375(平方米)
答:这个花圃的面积是375平方米。
【点评】此题主要考查梯形的周长公式、面积公式的灵活运用,关键是熟记公式。
梯形的面积》同步练习
一、填空题
1.梯形上底是5cm,下底是10cm,面积是30平方厘米,高是
cm。
2.有一个梯形的面积是48dm2,它的上底和下底的平均长度是24dm,这个梯形的高是
dm。
3.一个直角梯形的上底长5分米,下底长8分米,两条腰分别是4分米和5分米,这个直角梯形面积是
平方分米。
4.一堆钢管,已知最上层7根,最下层有19根,相邻两层之间相差1根,这堆钢管共有
根。
5.妈妈的手提包侧面的形状是个梯形,上底是18cm,下底是22cm,高是15cm,面积是
cm2。
6.一个梯形果园,上底是300米,下底是500米,高是100米。这个果园的面积等于
公顷。
二、单选题
7.一个梯形的上底增加10厘米,下底减少10厘米,高不变,梯形现在的面积( )
A.增加10平方厘米
B.减少10平方厘米
C.不变
D.无法确定
8.在图中,平行线间的三个图形,它们的面积相比( )
A.平行四边形的面积大
B.三角形的面积大
C.梯形的面积大
D.面积都相等
9.梯形的上底是8米,下底是3米,高是下底的2倍,这个梯形的面积是( )
A.22平方米
B.33平方米
C.66平方米
10.一个梯形的上底长36dm,如果补上一块底为64dm,面积为64dm2的三角形,就变成了一个平行四边形,这个梯形的面积是( )
A.20dm2
B.136dm2
C.272dm2
D.68dm2
11.一个梯形的面积是24平方米,高是8米,它的上、下底的和是( )
A.3米
B.4米
C.6米
D.8米
12.梯形的上底扩大到原来的3倍,下底也扩大到原来的3倍,高不变,那么它的面积( )
A.扩大到原来的3倍
B.扩大到原来的9倍
C.扩大到原来的6倍
D.不变
三、判断题
13.两个面积相等的梯形,形状和大小也一定相同。
(判断对错)
14.梯形的上底下底越长,面积越大.
.(判断对错)
15.梯形的面积等于平行四边形面积的一半.
.(判断对错)
16.一个梯形的上底、下底和高都扩大到它的2倍,那么面积扩大到原来的4倍.
(判断对错)
17.一个梯形上、下底的和是6dm,高是10dm,它的面积是30dm2.
(判断对错)
18.一个梯形的上底是6米,下底是8米,面积是42平方米,它的高是6米.
(判断对错)
四、计算题
19.计算图形的面积。
(1);
(2)。
20.计算图形的面积。(单位:厘米))
五、作图题
21.按要求在方格图中画图。
(1)画一个平行四边形,使它的面积与图中长方形的面积相等;
(2)画一个三角形,使它的面积是图中长方形的面积的一半;
(3)画一个梯形,使它的面积是图中长方形的面积的2倍。
22.按要求在格子图中画图(每个小方格表示1平方厘米)。
(1)画一个与已知平行四边形面积相等,底也相等三角形;
(2)以AB为下底,画一个面积为9平方厘米的梯形。
六、解决问题
23.爷爷在一块上底是120m,下底是180m,高是60m的梯形果园种果树,如果每棵果树占地面积10m2,这个果园一共可以种多少棵果树?
24.一块菜地一面靠墙,用62米的篱笆刚好把菜地的三条边围起来(如图),这块菜地的面积是多少平方米?
25.小冬家用50m长的竹篱笆,靠墙边围成了一块瓜地(见图).如果平均每平方米地可以栽种4棵瓜苗,这块地可以栽种多少棵瓜苗?
26.某建筑工地新购进一批钢管,堆成如下图的形状,共堆了10层。最上层堆9根,最下层堆18根,每相邻两层相差1根。这个工地一共购进多少根钢管?
27.一块白菜地的形状是梯形,上底是9米,下底是12米,高是18米.如果平均每棵白菜占地9平方分米,这块地一共可以种白菜多少棵?
28.如图,王大叔家用65米长的竹篱笆在一块靠墙的空地上围了一个花圃,这个花圃的面积是多少平方米?
参考答案与试题解析
一、填空题
1.【分析】根据梯形的面积公式:S=(a+b)h÷2,那么h=2S÷(a+b),把数据代入公式解答。
【解答】解:30×2÷(5+10)
=60÷15
=4(厘米)
答:高是4厘米。
故答案为:4。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
2.【分析】根据梯形的面积公式:S=(a+b)h÷2,那么h=2S÷(a+b),把数据代入公式解答。
【解答】解:48×2÷(24×2)
=96÷48
=2(分米)
答:这个梯形的高是2分米。
故答案为:2。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
3.【分析】根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【解答】解:(5+8)×4÷2
=13×4÷2
=26(平方分米)
答:这个直角梯形面积是26平方分米。
故答案为:26。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
4.【分析】已知最上层7根,最下层有19根,相邻两层之间相差1根,首先求出层数(高),层数=最下层的根数﹣最上层根数+1,根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【解答】解:(7+19)×(19﹣7+1)÷2
=26×13÷2
=169(根)
答:这堆钢管共有169根。
故答案为:169。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
5.【分析】根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【解答】解:(18+22)×15÷2
=40×15÷2
=300(平方厘米)
答:面积是300平方厘米。
故答案为:300。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
6.【分析】根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【解答】解:(300+500)×100÷2
=800×100÷2
=40000(平方米)
40000平方米=4公顷
答:这个果园的面积是4公顷。
故答案为:4。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
二、单选题
7.【分析】根据梯形的面积公式:S=(a+b)h÷2,一个梯形的上底增加10厘米,下底减少10厘米,高不变,也就是梯形上下底之和不变,所以梯形现在的面积与原来的面积相等。据此解答。
【解答】解:一个梯形的上底增加10厘米,下底减少10厘米,高不变,也就是梯形上下底之和不变,所以梯形现在的面积与原来的面积相等。
答:梯形现在的面积不变。
故选:C。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
8.【分析】在图中,三个图形的高相等,梯形的上底、下底、平行四边形的底、三角形的底都已知,再依据三者的面积公式即可判断它们的面积大小.
【解答】解:设高为h,
平行四边形的面积=4h=4h
三角形的面积=×8×h=4h
梯形面积=(2+6)×h÷2=4h
所以它们的面积相比,都相等;
故选:D。
【点评】此题主要考查等高的平行四边形、三角形和梯形的面积大小比较,将数据代入各自的面积公式即可求解.
9.【分析】高是下底的2倍,所以高是3×2=6米,根据梯形的面积=(上底+下底)×高÷2,代入数据计算即可解答.
【解答】解:(8+3)×3×2÷2
=11×6÷2
=33(平方米)
答:这个图形的面积是33平方米.
故选:B。
【点评】此题考查了梯形的面积公式的计算应用.
10.【分析】由“如果补上一块底为64dm,面积为64dm2的三角形,就变成了一个平行四边形”可得:平行四边形的底为(36+64)分米,利用三角形的面积公式即可求出三角形的高,也就是梯形的高,于是就可以利用梯形的面积公式求解.
【解答】解:64×2÷64=2(分米),
36+64=100(分米),
(36+100)×2÷2
=136×2÷2
=136(平方分米).
答:这个梯形的面积是136平方分米.
故选:B。
【点评】此题主要考查了三角形和梯形的面积的计算方法,关键是由题目条件先求出:梯形的下底和高的值.
11.【分析】根据梯形的面积公式:S=(a+b)h÷2,那么a+b=2S÷h,把数据代入公式解答。
【解答】解:24×2÷8
=48÷8
=6(米)
答:它的上、下底的和是6米。
故选:C。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
12.【分析】根据题意可知,梯形的上底和下底都扩大到原来的3倍,也就是说(上底+下底)的和扩大到原来的3倍,高不变,它的面积一定也扩大到原来的3倍。
【解答】解:设上底为a,下底为b,高为h,
原来的面积是:S=(a+b)×h÷2;
扩大后的面积是:
(a×3+b×3)×h÷2
=(a+b)×3×h÷2
=[(a+b)×h÷2]×3;
所以梯形的上底和下底都扩大到原来的3倍,高不变,它的面积也随之扩大到原来的3倍。
故选:A。
【点评】本题用到的知识点是:S=(a+b)×h÷2;两个加数都扩大几倍,它们的和也扩大几倍。
三、判断题
13.【分析】因为梯形的面积S=(a+b)×h÷2,即梯形的面积只与上底、下底和高的长度有关,而与梯形的形状无关,据此求解即可。
【解答】解:梯形的面积只与上底、下底和高的长度有关,而与梯形的形状无关,所以“两个面积相等的梯形,形状和大小也一定相同”的说法是错误的。
故答案为:×。
【点评】解决本题的关键在于知道梯形的面积只与上底、下底和高的长度有关。
14.【分析】根据梯形的面积公式=(上底+下底)×高÷2可知,梯形的面积由上底、下底、高的大小决定,如果梯形的上底、下底越长,而梯形的高最小,则梯形的面积不是最大,据此解答即可.
【解答】解:根据梯形的面积公式,梯形的面积由上底、下底、高三个要素确定,上底和下底越长不能说它们的面积就越大.
故判:×.
【点评】此题主要考查的是梯形面积公式的灵活应用.
15.【分析】缺少关键条件,梯形的面积是和它等底等高的平行四边形面积的一半.
【解答】解:因为梯形的面积是和它等底等高的平行四边形面积的一半.
故答案为:×.
【点评】此题主要考查梯形的面积是和它等底等高的平行四边形面积的一半.
16.【分析】依据梯形的面积=(a+b)×h÷2,若“梯形的上底、下底和高都扩大到它的2倍”,则梯形的上底为2a,下底为2b,高为2h,分别求出扩大前后梯形的面积,用扩大后的面积除以扩大前的面积即得扩大的倍数.
【解答】解:原梯形的面积为(a+b)×h÷2,
扩大后的面积为:(2a+2b)×2h÷2
=4[(a+b)×h÷2]
4[(a+b)×h÷2]÷[(a+b)×h÷2]=4倍,
所以一个梯形的上底、下底、高分别扩大2倍,它的面积扩大4倍.
所以题干说法正确.
故答案为:√.
【点评】此题主要考查梯形的面积公式的灵活运用.
17.【分析】根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式求出它的面积,然后与30平方分米进行比较即可.
【解答】解:6×10÷2
=60÷2
=30(平方分米)
答:它的面积是30平方分米.
故答案为:√.
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式.
18.【分析】根据梯形的面积公式:S=(a+b)h÷2,那么h=2S÷(+b),据此求出梯形的高,然后与6米进行比较。
【解答】解:42×2÷(6+8)
=84÷14
=6(米)
6=6
因此,题干中的计算是正确的。
故答案为:√。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
四、计算题
19.【分析】(1)根据梯形面积=(上底+下底)×高÷2,代入数据求解即可;
(2)该图形的面积=长方形的面积﹣三角形的面积,根据长方形面积=长×宽,三角形面积=底×高÷2,代入数据求解即可。
【解答】解:(1)(2.6+3.4)×5.2÷2
=6×5.2÷2
=31.2÷2
=15.6(平方米)
答:该图形的面积是15.6平方米。
(2)40×30﹣30×10÷2
=1200﹣150
=1050(平方厘米)
答:该图形的面积是1050平方厘米。
【点评】本题主要考查求解梯形面积和组合图形面积的方法。注意求组合图形面积时要将不规则图形转化为规则图形的面积差来求解。
20.【分析】根据梯形面积=(上底+下底)×高÷2,代入数据求解即可。
【解答】解:(6+8)×5÷2
=14×5÷2
=35(平方厘米)
答:该图形的面积是35平方厘米。
【点评】本题主要考查梯形面积公式的应用,解决本题的关键在于分清梯形的各部分名称。
五、作图题
21.【分析】(1)当平行四边形的底等于长方形的长,平行四边形的高等于长方形的宽时,它们的面积相等。据此画图。
(2)根据三角形的面积:S=ah÷2,要画一个三角形,使它的面积是图中长方形的面积的一半,这个三角形的底等于长方形的长,三角形的高等于长方形的宽。据此画图。
(3)根据梯形的面积公式:S=(a+b)h÷2,要使梯形的面积等于图中长方形的2倍,画法不唯一,可以画一个高是3厘米,上底是3厘米,下底是5厘米的图形。据此解答。
【解答】解:(1)画法不唯一。画图如下:
(2)画法不唯一。画图如下:
(3)画法不唯一。画图如下:
【点评】此题考查的目的是理解掌握平行四边形、三角形、梯形的特征,以及平行四边形、三角形、梯形的面积公式及应用。
22.【分析】(1)因为等底等高的三角形的面积是平行四边形面积的一半,要使三角形的面积等于平行四边形的面积,三角形的底等于平行四边形的底,那么三角形的高是平行四边形高的2倍。据此画图。
(2)根据梯形的面积公式:S=(a+b)h÷2,画法不唯一,可以画一个上底是4厘米,高是2厘米的梯形。
【解答】解:(1)画法不唯一。画图如下:
(2)画法不唯一。画图如下:
【点评】此题主要考查平行四边形、三角形、梯形面积公式的灵活运用,关键是熟记公式。
六、解决问题
23.【分析】根据梯形的面积公式:S=(a+b)h÷2,求出这块地的面积,然后根据“包含”除法的意义,用这块地面积除以每棵果树的占地面积即可。
【解答】解:(120+180)×60÷2÷10
=300×60÷2÷10
=9000÷10
=900(棵)
答:这个果园一共可以种果树900棵。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
24.【分析】用三条边的长度和42米减去高就是梯形上下底的和,然后再根据梯形面积=(上底+下底)×高÷2解答即可。
【解答】解:菜地为梯形:上底与下底的和:62﹣26=36(米),
36×26÷2=468(平方米)
答:这块菜地的面积是468平方米。
【点评】本题主要是利用梯形的面积公式S=(a+b)×h÷2解决问题。
25.【分析】用50m长的竹篱笆,靠墙边围成了一块瓜地,那么用50减去20就是围成的梯形上底与下底的和;根据梯形的面积公式求出梯形的面积,再乘平均每平方米栽种瓜苗的棵数,就是这块地可以栽种多少棵瓜苗.
【解答】解:(50﹣20)×20÷2×4
=30×40
=1200(棵)
答:这块地可以栽种1200棵瓜苗.
【点评】本题的主要考查了学生根据梯形的面积公式S=(a+b)×h÷2解答问题的能力.
26.【分析】根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【解答】解:(9+18)×10÷2
=27×10÷2
=135(根)
答:这个工地一共购进135根钢管。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
27.【分析】根据梯形的面积=(上底+下底)×高÷2,求出这块地的面积,再求出这个面积里面有几个9平方分米,即可求出一共有几棵白菜,据此计算即可解答.
【解答】解:9平方分米=0.09平方米
(9+12)×18÷2÷0.09
=21×18÷2÷0.09
=189÷0.09
=2100(棵)
答:这块地一共可以种白菜2100棵.
【点评】此题考查了梯形的面积公式的计算应用.
28.【分析】通过观察图形可知,一面靠墙,用65米长的篱笆围成一个直角梯形,梯形的高是15米,那么梯形上底、下底之和是(65﹣15)米,根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【解答】解:(65﹣15)×15÷2
=50×15÷2
=375(平方米)
答:这个花圃的面积是375平方米。
【点评】此题主要考查梯形的周长公式、面积公式的灵活运用,关键是熟记公式。
