苏科版七年级数学上册 2.7 有理数的乘方课件(18张PPT)
文档属性
| 名称 | 苏科版七年级数学上册 2.7 有理数的乘方课件(18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 22:26:39 | ||
图片预览






文档简介
(共18张PPT)
有理数的乘方
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“就在这个棋盘上放一些米粒吧。
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“就在这个棋盘上放一些米粒吧。
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“就在这个棋盘上放一些米粒吧。
棋盘上的故事
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“就在这个棋盘上放一些米粒吧。第1格放1粒,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒……一直到第64格。”
“你真傻!就要这么一点米?”,国王哈哈大笑。这位大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗?
一张白纸,将这张纸对折1次,2次,3次,
观察可以得到几层?
结论:将这张白纸对折1次,可以得到
层;
将这张白纸对折2次,可以得到
层;
将这张白纸对折3次,可以得到
层;
2
2
4
2
×2
8
2
×2
×2
想一想:若对折5次、10次、20次,又可以得到几层?
读作:2的平方(或二次方)
读作:2的立方(或二的三次方)
…
…
读作:2的5次方
1×1×1×1×1×1×1=
0.2
×0.2
×0.2=
(-3)
×(-3)×(-3)=
练习1:把以下乘法式子写成乘方的形式。
试一试,你会了吗?
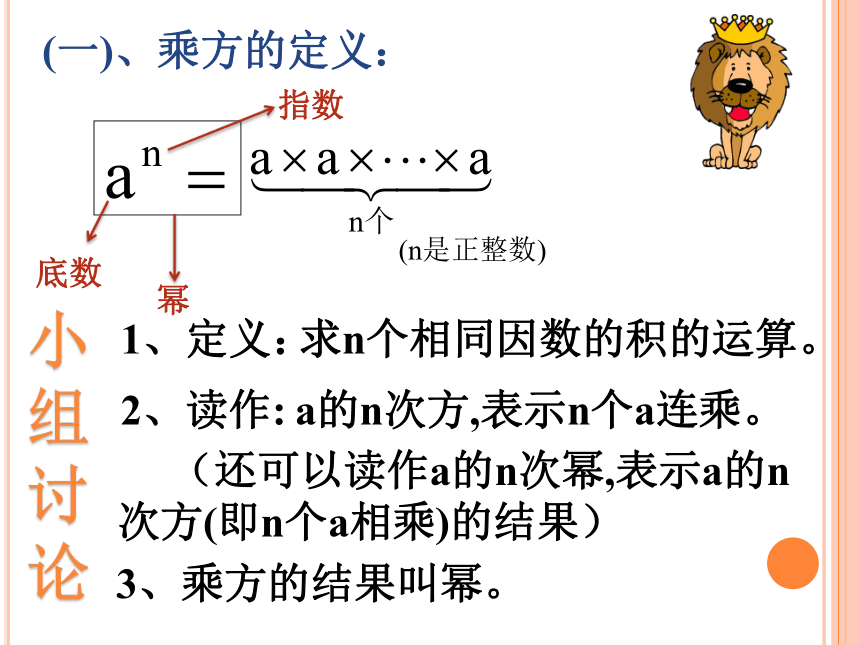
(一)、乘方的定义:
(n是正整数)
底数
指数
幂
求n个相同因数的积的运算。
3、乘方的结果叫幂。
a的n次方,表示n个a连乘。
(还可以读作a的n次幂,表示a的n
次方(即n个a相乘)的结果)
1、定义:
2、读作:
练习2:根据下列文字,写出相应的算式。
(1)10的五次方;
(2)-3的四次方;
(3)3的四次方的相反数;
(4)3的相反数的四次方;
练习3:小组PK抢答,说出底数和指数,答对者加分。
停止
开始
例:计算下列有理数的乘方。
3、负数的奇数次幂是负数;
2、负数的偶数次幂是正数;
1、正数的任何次幂都是正数;
4、0的任何正整数次幂都是0。
计算下列有理数的乘方:
①
②
③
4
5
6
运算
加法
减法
乘法
除法
结果
和
差
积
商
幂
乘方也是一种运算,到目前我们一共学习了五种运算:
乘方
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“就在这个棋盘上放一些米粒吧。
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“就在这个棋盘上放一些米粒吧。
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“就在这个棋盘上放一些米粒吧。
棋盘上的故事
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“就在这个棋盘上放一些米粒吧。第1格放1粒,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒……一直到第64格。”
“你真傻!就要这么一点米?”,国王哈哈大笑。这位大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗?
第一格2粒米,
第二格4粒米,
第三格8粒米,
第四格16粒米,
…
第十八格,
…
…
第六十四格,
=?粒米
262144
…
?粒米
18446744073709551616
一斤米约有10000粒。
(约为1844万亿斤)
而我国去年一年的粮食产量为9680亿斤,即0.968万亿斤。
所以,国王的粮库当然不够啦!
第64格有18446744073709551616粒米,
约有1844674407370955斤。
学习了本节课,你
有哪些收获?
“乘方”精神:虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。
一张纸的厚度为0.1毫米,如果将它连续对折50次,会有多厚?其厚度能不能超过珠穆玛朗峰的高度?
有理数的乘方
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“就在这个棋盘上放一些米粒吧。
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“就在这个棋盘上放一些米粒吧。
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“就在这个棋盘上放一些米粒吧。
棋盘上的故事
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“就在这个棋盘上放一些米粒吧。第1格放1粒,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒……一直到第64格。”
“你真傻!就要这么一点米?”,国王哈哈大笑。这位大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗?
一张白纸,将这张纸对折1次,2次,3次,
观察可以得到几层?
结论:将这张白纸对折1次,可以得到
层;
将这张白纸对折2次,可以得到
层;
将这张白纸对折3次,可以得到
层;
2
2
4
2
×2
8
2
×2
×2
想一想:若对折5次、10次、20次,又可以得到几层?
读作:2的平方(或二次方)
读作:2的立方(或二的三次方)
…
…
读作:2的5次方
1×1×1×1×1×1×1=
0.2
×0.2
×0.2=
(-3)
×(-3)×(-3)=
练习1:把以下乘法式子写成乘方的形式。
试一试,你会了吗?
(一)、乘方的定义:
(n是正整数)
底数
指数
幂
求n个相同因数的积的运算。
3、乘方的结果叫幂。
a的n次方,表示n个a连乘。
(还可以读作a的n次幂,表示a的n
次方(即n个a相乘)的结果)
1、定义:
2、读作:
练习2:根据下列文字,写出相应的算式。
(1)10的五次方;
(2)-3的四次方;
(3)3的四次方的相反数;
(4)3的相反数的四次方;
练习3:小组PK抢答,说出底数和指数,答对者加分。
停止
开始
例:计算下列有理数的乘方。
3、负数的奇数次幂是负数;
2、负数的偶数次幂是正数;
1、正数的任何次幂都是正数;
4、0的任何正整数次幂都是0。
计算下列有理数的乘方:
①
②
③
4
5
6
运算
加法
减法
乘法
除法
结果
和
差
积
商
幂
乘方也是一种运算,到目前我们一共学习了五种运算:
乘方
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“就在这个棋盘上放一些米粒吧。
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“就在这个棋盘上放一些米粒吧。
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“就在这个棋盘上放一些米粒吧。
棋盘上的故事
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“就在这个棋盘上放一些米粒吧。第1格放1粒,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒……一直到第64格。”
“你真傻!就要这么一点米?”,国王哈哈大笑。这位大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗?
第一格2粒米,
第二格4粒米,
第三格8粒米,
第四格16粒米,
…
第十八格,
…
…
第六十四格,
=?粒米
262144
…
?粒米
18446744073709551616
一斤米约有10000粒。
(约为1844万亿斤)
而我国去年一年的粮食产量为9680亿斤,即0.968万亿斤。
所以,国王的粮库当然不够啦!
第64格有18446744073709551616粒米,
约有1844674407370955斤。
学习了本节课,你
有哪些收获?
“乘方”精神:虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。
一张纸的厚度为0.1毫米,如果将它连续对折50次,会有多厚?其厚度能不能超过珠穆玛朗峰的高度?
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
