苏科版九年级数学上册 1.3 一元二次方程的根与系数的关系(共24张PPT)
文档属性
| 名称 | 苏科版九年级数学上册 1.3 一元二次方程的根与系数的关系(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 942.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
一元二次方程的根与系数的关系
请说出一个有解的一元二次方程,我就能说出它的两根和与积。
一元二次方程
ax2+bx+c=0(a≠0)
的求根公式:
x=
(b2-4ac≥0)
一元二次方程的根与系数的关系
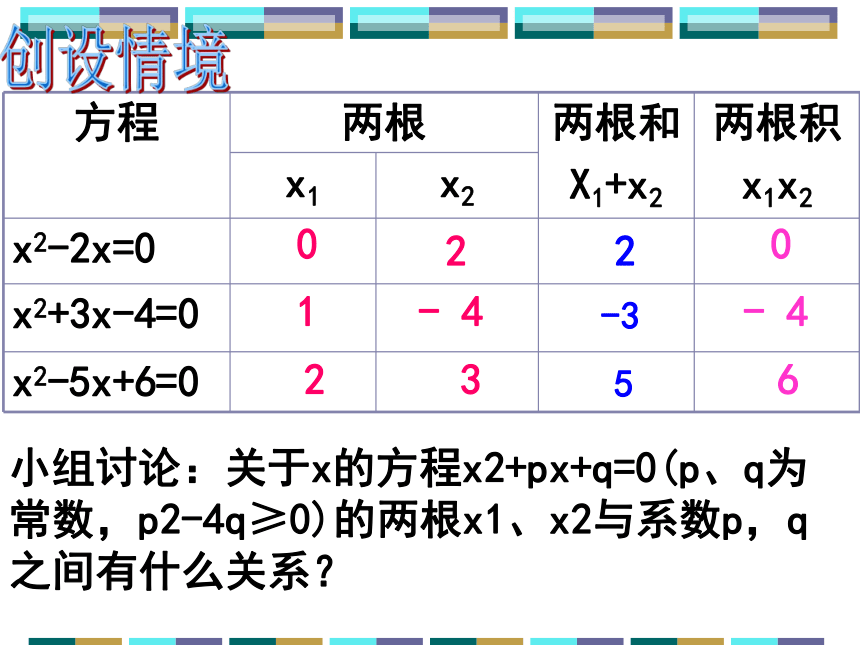
(1)x2-2x=0
(2)
x2+3x-4=0
解下列方程
(3)x2-5x+6=0
X1=0;
X2=2
X1=1;
X2=-4
X1=2;
X2=3
方程
两根
两根和
X1+x2
两根积
x1x2
x1
x2
x2-2x=0
x2+3x-4=0
x2-5x+6=0
0
2
0
2
1
-3
-
4
-
4
2
3
5
6
小组讨论:关于x的方程x2+px+q=0(p、q为常数,p2-4q≥0)的两根x1、x2与系数p,q之间有什么关系?
关于x的方程x2+px+q=0(p、q为常数,p2-4q≥0)的两根x1、x2与系数p,q的关系是:
x1+x2=-p;
x1x2=q
思考:如果一元二次方程二次项的系数不为1,根与系数之间又有怎样的关系呢?
∵
∴
∴
若一元二次方程
ax2+bx+c=0(a≠0)的两根为x1、x2,
则
.
.
怎么证明这个结论呢?
X1+x2=
+
=
=
-
X1x2=
●
=
=
=
证明:设ax2+bx+c=0(a≠0)的两根为x1、x2,则
一元二次方程的根与系数的关系
如果方程ax2+bx+c=0(a≠0)的两个根是x1
,
x2
,
那么x1+x2=
,
x1x2
=
-
注:能用公式的前提条件为△=b2-4ac≥0
在使用根与系数的关系时,应注意:
⑴不是一般式的要先化成一般式;
⑵在使用X1+X2=-
时,
注意“-
”不要漏写。
x1+x2=3
x1x2=
-1
x1+x2=
-1.5
x1+x2=6
x1x2=
-2.5
x1x2=0
例1、不解方程,口答下列方程的两根和与两根积:
(1)
(2)
(3)
(4)
(5)
x1+x2=0
x1x2=
-2
x1+x2=
-2
x1x2=
1
(1)
变式1、方程2x2-3x+1=0的两根记作x1,x2,
不解方程,求下列式子的值:
(2)
(3)
变式2、已知方程2x2+kx-9=0的一个根是-3
,求它的另一个根及k的值.
变式2、已知方程2x2+kx-9=0的一个根是-3
,求它的另一个根及k的值.
变式3、已知
的两个实数根,求
的值。
例2.已知方程x2+kx+k+2=0的两个实数根是
x1,x2且x12+x22=4
,
求k的值.
解:由根与系数的关系得
x1+x2=-k,
x1x2=k+2
又
x12+
x2
2
=
4
即(x1+
x2)2
-2x1x2=4
K2-
2(k+2)=4
K2-2k-8=0
∵
△=
K2-4k-8
当k=4时,
△=-8<0
∴k=4(舍去)
当k=-2时,△=4>0
∴
k=-2
解得:k=4
或k=-2
(14泗洪)关于x的一元二次方程x2-mx+2m-1=0的两个实数根分别是x1、x2,且x12+x22=7,求(x1-x2)2的值。
解:由题意,得:x1+x2=m,x1x2=2m-1;
则:(x1+x2)2=x12+2x1x2+x22,
即m2=7+2(2m-1),
解得m1=-1,m2=5;
当m=5时,△=m2-4(2m-1)=25-4×9<0,不合题意;
故m=-1,x1+x2=-1,x1x2=-3;
∴(x1-x2)2=(x1+x2)2-4x1x2=1+12=13.
课堂检测
1、已知方程x2+px+q=0的两根之和为4,两根之积为-3,则p和q的值为(
)
A.p=8,q=-6
B.p=-4,q=-3
C.p=-3,q=4
D.p=-8,q=-6
B
课堂检测
2、已知方程3x2+6x-m=0的一个根为1,则方程的另一个根及m的值为(
)
A.x=-3,m=-9
B.x=3,m=-9
C.x=-3,m=
9
D.x=3,m=9
C
课堂检测
3、设x1、x2是方程x2-4x+1=0的两个根,则
x1
+
x2=
x1x2
=
__
_
x12+x22
=
(x1
+
x2)2
-
=
(x1-x2)2
=
(x1
+
x2)2
-
=
4
1
2x1x2
4x1x2
14
12
课堂检测
4、已知关于x的方程k2x2+(2k-1)x+1=0有两个不相等的实数根x1、x2.
⑴求k的取值范围;
⑵k为何值时,x1与x2互为倒数.
(1)K<1/4且K≠0
(2)K=-1
5、(选做题)在解方程x2+px+q=0时,小张看错了p,解得方程的根为1与-3;小王看错了q,
解得方程的根为4与-2,这个方程的正确根应该是什么?
课堂检测
X1=3,
X2=-1
2、熟练掌握根与系数的关系;
3、灵活运用根与系数关系解决问题.
1.一元二次方程根与系数的关系?
小结:
____年___月___日
星期____
天气_____
学习课题:_________
知识归纳与整理:____
_______________________
自我评价:___________
悄悄话:老师我想对你说____________________________________________________
有那些数学思想方法_______________________
我的收获与困惑_________
_______________________
一元二次方程的根与系数的关系
请说出一个有解的一元二次方程,我就能说出它的两根和与积。
一元二次方程
ax2+bx+c=0(a≠0)
的求根公式:
x=
(b2-4ac≥0)
一元二次方程的根与系数的关系
(1)x2-2x=0
(2)
x2+3x-4=0
解下列方程
(3)x2-5x+6=0
X1=0;
X2=2
X1=1;
X2=-4
X1=2;
X2=3
方程
两根
两根和
X1+x2
两根积
x1x2
x1
x2
x2-2x=0
x2+3x-4=0
x2-5x+6=0
0
2
0
2
1
-3
-
4
-
4
2
3
5
6
小组讨论:关于x的方程x2+px+q=0(p、q为常数,p2-4q≥0)的两根x1、x2与系数p,q之间有什么关系?
关于x的方程x2+px+q=0(p、q为常数,p2-4q≥0)的两根x1、x2与系数p,q的关系是:
x1+x2=-p;
x1x2=q
思考:如果一元二次方程二次项的系数不为1,根与系数之间又有怎样的关系呢?
∵
∴
∴
若一元二次方程
ax2+bx+c=0(a≠0)的两根为x1、x2,
则
.
.
怎么证明这个结论呢?
X1+x2=
+
=
=
-
X1x2=
●
=
=
=
证明:设ax2+bx+c=0(a≠0)的两根为x1、x2,则
一元二次方程的根与系数的关系
如果方程ax2+bx+c=0(a≠0)的两个根是x1
,
x2
,
那么x1+x2=
,
x1x2
=
-
注:能用公式的前提条件为△=b2-4ac≥0
在使用根与系数的关系时,应注意:
⑴不是一般式的要先化成一般式;
⑵在使用X1+X2=-
时,
注意“-
”不要漏写。
x1+x2=3
x1x2=
-1
x1+x2=
-1.5
x1+x2=6
x1x2=
-2.5
x1x2=0
例1、不解方程,口答下列方程的两根和与两根积:
(1)
(2)
(3)
(4)
(5)
x1+x2=0
x1x2=
-2
x1+x2=
-2
x1x2=
1
(1)
变式1、方程2x2-3x+1=0的两根记作x1,x2,
不解方程,求下列式子的值:
(2)
(3)
变式2、已知方程2x2+kx-9=0的一个根是-3
,求它的另一个根及k的值.
变式2、已知方程2x2+kx-9=0的一个根是-3
,求它的另一个根及k的值.
变式3、已知
的两个实数根,求
的值。
例2.已知方程x2+kx+k+2=0的两个实数根是
x1,x2且x12+x22=4
,
求k的值.
解:由根与系数的关系得
x1+x2=-k,
x1x2=k+2
又
x12+
x2
2
=
4
即(x1+
x2)2
-2x1x2=4
K2-
2(k+2)=4
K2-2k-8=0
∵
△=
K2-4k-8
当k=4时,
△=-8<0
∴k=4(舍去)
当k=-2时,△=4>0
∴
k=-2
解得:k=4
或k=-2
(14泗洪)关于x的一元二次方程x2-mx+2m-1=0的两个实数根分别是x1、x2,且x12+x22=7,求(x1-x2)2的值。
解:由题意,得:x1+x2=m,x1x2=2m-1;
则:(x1+x2)2=x12+2x1x2+x22,
即m2=7+2(2m-1),
解得m1=-1,m2=5;
当m=5时,△=m2-4(2m-1)=25-4×9<0,不合题意;
故m=-1,x1+x2=-1,x1x2=-3;
∴(x1-x2)2=(x1+x2)2-4x1x2=1+12=13.
课堂检测
1、已知方程x2+px+q=0的两根之和为4,两根之积为-3,则p和q的值为(
)
A.p=8,q=-6
B.p=-4,q=-3
C.p=-3,q=4
D.p=-8,q=-6
B
课堂检测
2、已知方程3x2+6x-m=0的一个根为1,则方程的另一个根及m的值为(
)
A.x=-3,m=-9
B.x=3,m=-9
C.x=-3,m=
9
D.x=3,m=9
C
课堂检测
3、设x1、x2是方程x2-4x+1=0的两个根,则
x1
+
x2=
x1x2
=
__
_
x12+x22
=
(x1
+
x2)2
-
=
(x1-x2)2
=
(x1
+
x2)2
-
=
4
1
2x1x2
4x1x2
14
12
课堂检测
4、已知关于x的方程k2x2+(2k-1)x+1=0有两个不相等的实数根x1、x2.
⑴求k的取值范围;
⑵k为何值时,x1与x2互为倒数.
(1)K<1/4且K≠0
(2)K=-1
5、(选做题)在解方程x2+px+q=0时,小张看错了p,解得方程的根为1与-3;小王看错了q,
解得方程的根为4与-2,这个方程的正确根应该是什么?
课堂检测
X1=3,
X2=-1
2、熟练掌握根与系数的关系;
3、灵活运用根与系数关系解决问题.
1.一元二次方程根与系数的关系?
小结:
____年___月___日
星期____
天气_____
学习课题:_________
知识归纳与整理:____
_______________________
自我评价:___________
悄悄话:老师我想对你说____________________________________________________
有那些数学思想方法_______________________
我的收获与困惑_________
_______________________
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
