苏科版九年级数学上册 2.6 正多边形与圆(共14张PPT)
文档属性
| 名称 | 苏科版九年级数学上册 2.6 正多边形与圆(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 07:59:06 | ||
图片预览






文档简介
(共14张PPT)
2.6正多边形和圆
操作一
(课前准备)
利用手边的工具(直尺、三角板、量角器、圆规……)
画一个边长为2cm的正三角形;
画一个边长为2cm的正方形。
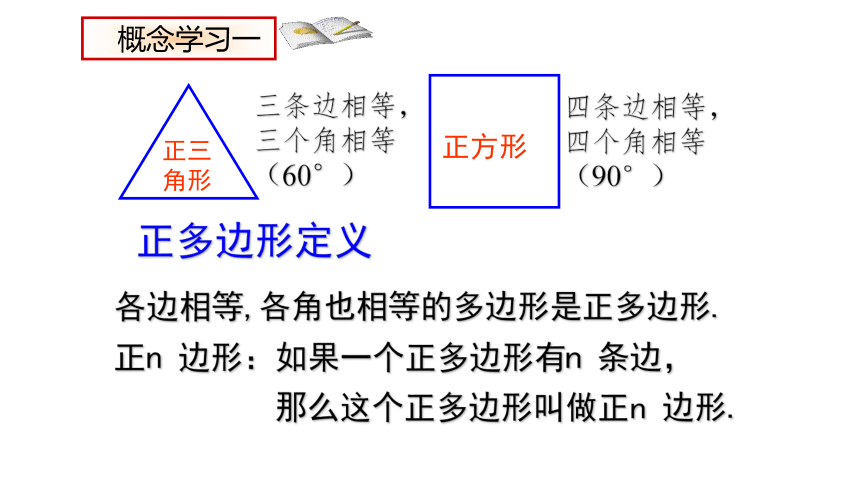
各边相等,各角也相等的多边形是正多边形.
正n
边形:如果一个正多边形有n
条边,
那么这个正多边形叫做正n
边形.
三条边相等,三个角相等(60°)
四条边相等,四个角相等(90°)
正三角形
正方形
正多边形定义
概念学习一
欣赏
概念辨析
能否说各边相等的多边形是正多边形吗?
或者说各角相等的多边形是正多边形吗?为什么?
分类讨论:分成边数等于3,边数大于3两种情况进行讨论
菱形是正多边形吗?矩形是正多边形吗?为什么?
想一想
注:判定一个多边形(边数大于3)是正多边形必须同时具备“各边相等”
、“各角相等”
的条件。
操作二
你会画正五边形吗?
谈谈你的画法,说说你的理由。
如图,用量角器把⊙O五等分(每两个相邻等分点间的弧均为72o),依次连接各分点得到正五边形ABCDE.
∴
AB=BC=CD=DE=EA
,
∴
∠A=∠B.
·
A
B
C
D
E
O
同理∠B=∠C=∠D=∠E.
∴
五边形ABCD是正五边形.
⌒
⌒
⌒
⌒
⌒
证明
∵
AB=BC=CD=DE=EA
,
⌒
⌒
BCE=CDA
如何画正六边形,正七边形,正八边形……正n边形?
一般地,只要用量角器把一个圆n(
n
≥3)等分,依次连接各等分点就能得到这个圆的内接正n边形,这个圆就是这个正多边形的外接圆.
理由:∵⊙O被
n等分,
∴A1A2=A2A3=A3A4=…=An-1An,
∴ 多边形A1A2A3A4…An是正多边形.
An
A1
A2
A3
A4
A5
A6
A7
O
⌒
∴
A1A2=A2A3=A3A4
=
…=
An-1An
=AnA1
⌒
⌒
⌒
⌒
⌒
∴
A2A3An=A3A4A1
=A4A5A2
=…=
A1A2An-1
⌒
⌒
⌒
探索新知
③正多边形每一边所对的圆心角叫做正多边形的中心角(即∠AOB
)
①我们把一个正多边形的外接圆的圆心叫做这个正多边形的中心(即点O)
②外接圆的半径叫做正多边形的半径(即OA)
④中心到正多边形的一边的距离叫做正多边形的边心距
O
·
中心角
半径R
边心距r
A
B
C
D
E
F
M
概念学习二
有一个亭子,它的地基半径为4m的正六边形,求地基的周长和面积.
解:
连接OB、OC.如图由于ABCDEF是正六边形,所以
∠BOC=
,∵OB=OC,
△OBC是等边三角形,∴BC=OB=4.
因此,亭子地基的周长
l
=4×6=24(m).
过点O作PO⊥BC,垂足为P.
在Rt△OPC中,OC=4,
PC=
亭子地基的面积S=
×
×2
×6=24
O
A
B
C
D
E
F
P
例题
图1中连接对角线AC、AD,并求AC、AD的长.
变式1、
变式2、
利用图1作一个圆内接等边三角形,并求出该三角形的边长.
变式3、
利用图1作一个圆内接正方形AGDH,如果点H在弧BC上,那么BH是该圆的内接正十二边形的一边吗?为什么?
提升
如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
设D是AB边上一点,在图中作出一个
(1)正三角形DFH,使点F,点H分别在边BC和AC上.
(2)正六边形DEFGHI,使点F,点H分别在边BC和AC上.
2.6正多边形和圆
操作一
(课前准备)
利用手边的工具(直尺、三角板、量角器、圆规……)
画一个边长为2cm的正三角形;
画一个边长为2cm的正方形。
各边相等,各角也相等的多边形是正多边形.
正n
边形:如果一个正多边形有n
条边,
那么这个正多边形叫做正n
边形.
三条边相等,三个角相等(60°)
四条边相等,四个角相等(90°)
正三角形
正方形
正多边形定义
概念学习一
欣赏
概念辨析
能否说各边相等的多边形是正多边形吗?
或者说各角相等的多边形是正多边形吗?为什么?
分类讨论:分成边数等于3,边数大于3两种情况进行讨论
菱形是正多边形吗?矩形是正多边形吗?为什么?
想一想
注:判定一个多边形(边数大于3)是正多边形必须同时具备“各边相等”
、“各角相等”
的条件。
操作二
你会画正五边形吗?
谈谈你的画法,说说你的理由。
如图,用量角器把⊙O五等分(每两个相邻等分点间的弧均为72o),依次连接各分点得到正五边形ABCDE.
∴
AB=BC=CD=DE=EA
,
∴
∠A=∠B.
·
A
B
C
D
E
O
同理∠B=∠C=∠D=∠E.
∴
五边形ABCD是正五边形.
⌒
⌒
⌒
⌒
⌒
证明
∵
AB=BC=CD=DE=EA
,
⌒
⌒
BCE=CDA
如何画正六边形,正七边形,正八边形……正n边形?
一般地,只要用量角器把一个圆n(
n
≥3)等分,依次连接各等分点就能得到这个圆的内接正n边形,这个圆就是这个正多边形的外接圆.
理由:∵⊙O被
n等分,
∴A1A2=A2A3=A3A4=…=An-1An,
∴ 多边形A1A2A3A4…An是正多边形.
An
A1
A2
A3
A4
A5
A6
A7
O
⌒
∴
A1A2=A2A3=A3A4
=
…=
An-1An
=AnA1
⌒
⌒
⌒
⌒
⌒
∴
A2A3An=A3A4A1
=A4A5A2
=…=
A1A2An-1
⌒
⌒
⌒
探索新知
③正多边形每一边所对的圆心角叫做正多边形的中心角(即∠AOB
)
①我们把一个正多边形的外接圆的圆心叫做这个正多边形的中心(即点O)
②外接圆的半径叫做正多边形的半径(即OA)
④中心到正多边形的一边的距离叫做正多边形的边心距
O
·
中心角
半径R
边心距r
A
B
C
D
E
F
M
概念学习二
有一个亭子,它的地基半径为4m的正六边形,求地基的周长和面积.
解:
连接OB、OC.如图由于ABCDEF是正六边形,所以
∠BOC=
,∵OB=OC,
△OBC是等边三角形,∴BC=OB=4.
因此,亭子地基的周长
l
=4×6=24(m).
过点O作PO⊥BC,垂足为P.
在Rt△OPC中,OC=4,
PC=
亭子地基的面积S=
×
×2
×6=24
O
A
B
C
D
E
F
P
例题
图1中连接对角线AC、AD,并求AC、AD的长.
变式1、
变式2、
利用图1作一个圆内接等边三角形,并求出该三角形的边长.
变式3、
利用图1作一个圆内接正方形AGDH,如果点H在弧BC上,那么BH是该圆的内接正十二边形的一边吗?为什么?
提升
如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
设D是AB边上一点,在图中作出一个
(1)正三角形DFH,使点F,点H分别在边BC和AC上.
(2)正六边形DEFGHI,使点F,点H分别在边BC和AC上.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
