山东诸城一中2011-2012学年度高二下学期期末考试 数学文
文档属性
| 名称 | 山东诸城一中2011-2012学年度高二下学期期末考试 数学文 |  | |
| 格式 | zip | ||
| 文件大小 | 9.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-01 11:19:55 | ||
图片预览



文档简介
山东诸城一中
2011—2012学年度下学期期末考试
高二数学(文)试题
本试卷分Ⅰ卷和第Ⅱ卷两部分,满分150分,考试时间120分钟,考试结束后,将本试卷和答题卡一并交回。
注意事项:
答题前,考生务必将用0.5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置上。
2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试卷上。
第Ⅰ卷(选择题,共60分)
可能用到的公式或数据:
(1)具有线性相关关系的两个变量的回归直线方程其中
0.05 0.025 0.01
3.841 3.841 6.635
(2)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项
是符合题目要求的。
1.已知i是虚数单位,则 ( )
A. B. C. D.
2.抛物线的焦点坐标是 ( )
A.(1,0) B.( C.( D.
3.函数的导数为 ( )
A. B.
C. D.
4.命题:“若则”的否命题是 ( )
A.若,则 B.若则
C.若,则 D.若则
5.=-1是直线和直线垂直的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.若直线 ( )
A. B.[-1,3]
C.[-3,1] D.
7.下面使用类比推理正确的是 ( )
A.“若a·3=b·3,则a=b”类推出“若a·0=b·0,则a=b”
B.“若(a+b)c=ac+bc”类推出“(a·b)c=ac·bc”
C.“若(a+b)c=ac+bc”类推出“”
D.“”类推出“”
8.已知双曲线的离心率为2,一个焦点与抛物线的焦点相同,则双曲线的渐近方程为 ( )
A. B. C. D.
9.在(上单调递减,那么实数a的取值范围是( )
A.(0,1) B.(0,) C. D.
10.有人收集了春节期间的平均气温x与某取暖商品销售额y的有关数据如下表:
平均气温(℃) -2 -3 -5 -6
销售额(万元) 20 23 27 30
根据以上数据,用线性回归的方法,求得销售额y与平均气温x之间线性回归方程
。则预测平均气温为-8℃时该商品销售额为 ( )
A.34.6万元 B.35.6万元 C.36.6万元 D.37.6万元
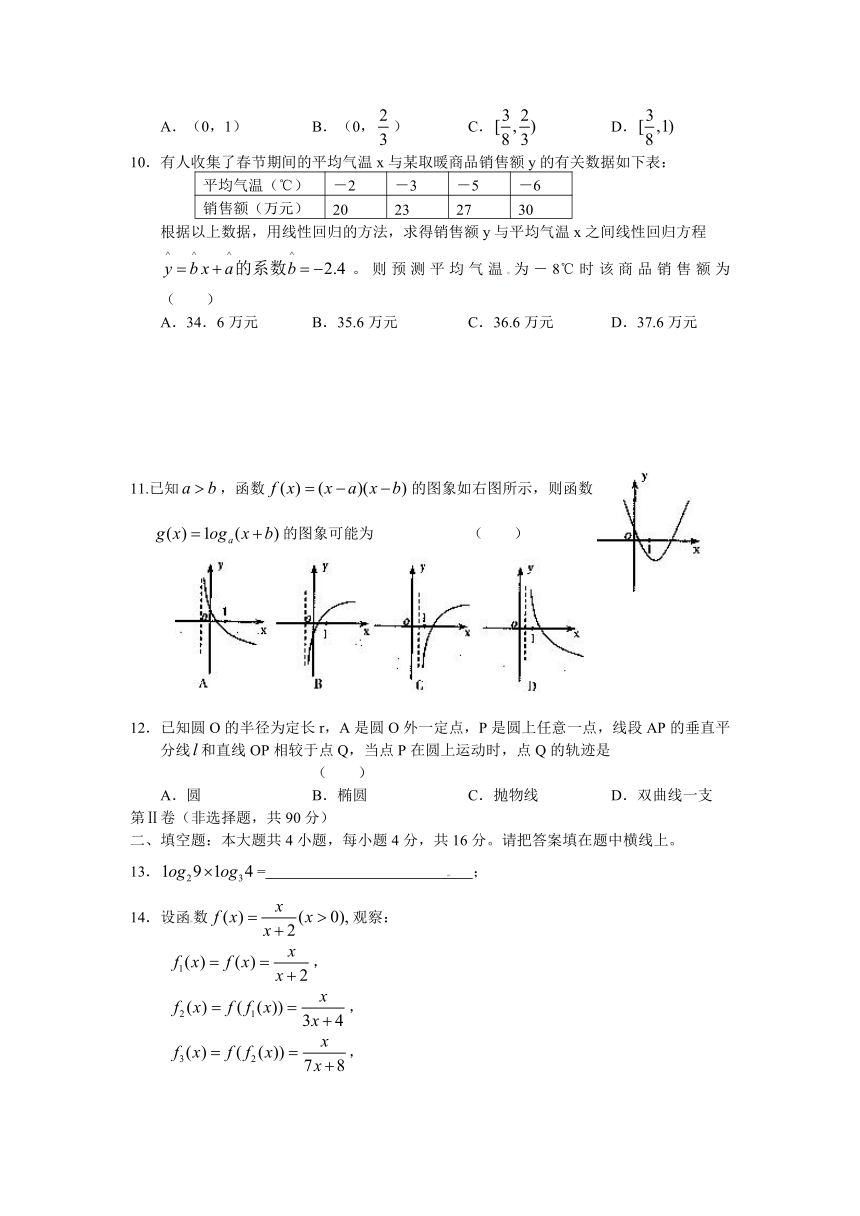
11.已知,函数的图象如右图所示,则函数
的图象可能为 ( )
12.已知圆O的半径为定长r,A是圆O外一定点,P是圆上任意一点,线段AP的垂直平分线和直线OP相较于点Q,当点P在圆上运动时,点Q的轨迹是 ( )
A.圆 B.椭圆 C.抛物线 D.双曲线一支
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分。请把答案填在题中横线上。
13.= ;
14.设函数观察:
,
,
,
,
……
根据以上事实,由归纳推理可得:
当= ;
15.已知双曲线的顶点与焦点分别是椭圆的焦点与顶点,若双曲线的离心率为2,则椭圆离心率为 ;
16.已知函数时,则下列结论正确的是 。
①;
②;
③;
④
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
命题p:方程有两个不等的正实数根,命题q:方程无实数根.若“p且q”为真命题,求m的取值范围.
18.(本小题满分12分)
在对人们休闲的一次调查中,共调查了124人,其中女性70人,男性54人,女性中有43人主要的休闲方式是看电视,另外27人的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(I)根据以上数据建立一个2×2的列联表;
(Ⅱ)检验性别是否与休闲方式有关,可靠性有多大?
19.(本小题满分12分)
已知顶点是坐标原点,对称轴是x轴的抛物线经过点M().
(I)求抛物线的标准方程;
(Ⅱ)直线过点P(l,0),且与抛物线交于不同两点A,B,若=5,求直线的方程.
20.(本小题满分12分) 、
已知函数,a∈R
(I)若函数f(x)是R上的单调递增函数,求实数a的取值范围;
(Ⅱ)若是f(x)的一个极值点,求f(x)在R上的极大值与极小值.
21.(本小题满分13分)
已知直线:mx-2y+2m=O(m∈R)和椭圆,椭圆C的离心率为,连接椭圆的四个顶点形成四边形的面积为
(I)求椭圆C的方程,
(Ⅱ)记直线经过的定点为Q,过点Q作斜率为k的直线与椭圆C有两个不同的交点,求实数k的取值范围;
(Ⅲ)设直线与y轴的交点为P,M为椭圆C上的动点,线段PM长度的最大值为f(m),求f(m)的表达式.
22.(本小题满分13分)
函数
(I)如果函数g(x)单调减区调为(一,1),求函数g(x)解析式;
(Ⅱ)在(I)的条件下,求函数y=g(x)图彖过点p(1,1)的切线方程;
(Ⅲ)若,使关于x的不等式2f(x)≥(x)+2成立,求实数a取值范围.
2011—2012学年度下学期期末考试
高二数学(文)试题
本试卷分Ⅰ卷和第Ⅱ卷两部分,满分150分,考试时间120分钟,考试结束后,将本试卷和答题卡一并交回。
注意事项:
答题前,考生务必将用0.5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置上。
2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试卷上。
第Ⅰ卷(选择题,共60分)
可能用到的公式或数据:
(1)具有线性相关关系的两个变量的回归直线方程其中
0.05 0.025 0.01
3.841 3.841 6.635
(2)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项
是符合题目要求的。
1.已知i是虚数单位,则 ( )
A. B. C. D.
2.抛物线的焦点坐标是 ( )
A.(1,0) B.( C.( D.
3.函数的导数为 ( )
A. B.
C. D.
4.命题:“若则”的否命题是 ( )
A.若,则 B.若则
C.若,则 D.若则
5.=-1是直线和直线垂直的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.若直线 ( )
A. B.[-1,3]
C.[-3,1] D.
7.下面使用类比推理正确的是 ( )
A.“若a·3=b·3,则a=b”类推出“若a·0=b·0,则a=b”
B.“若(a+b)c=ac+bc”类推出“(a·b)c=ac·bc”
C.“若(a+b)c=ac+bc”类推出“”
D.“”类推出“”
8.已知双曲线的离心率为2,一个焦点与抛物线的焦点相同,则双曲线的渐近方程为 ( )
A. B. C. D.
9.在(上单调递减,那么实数a的取值范围是( )
A.(0,1) B.(0,) C. D.
10.有人收集了春节期间的平均气温x与某取暖商品销售额y的有关数据如下表:
平均气温(℃) -2 -3 -5 -6
销售额(万元) 20 23 27 30
根据以上数据,用线性回归的方法,求得销售额y与平均气温x之间线性回归方程
。则预测平均气温为-8℃时该商品销售额为 ( )
A.34.6万元 B.35.6万元 C.36.6万元 D.37.6万元
11.已知,函数的图象如右图所示,则函数
的图象可能为 ( )
12.已知圆O的半径为定长r,A是圆O外一定点,P是圆上任意一点,线段AP的垂直平分线和直线OP相较于点Q,当点P在圆上运动时,点Q的轨迹是 ( )
A.圆 B.椭圆 C.抛物线 D.双曲线一支
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分。请把答案填在题中横线上。
13.= ;
14.设函数观察:
,
,
,
,
……
根据以上事实,由归纳推理可得:
当= ;
15.已知双曲线的顶点与焦点分别是椭圆的焦点与顶点,若双曲线的离心率为2,则椭圆离心率为 ;
16.已知函数时,则下列结论正确的是 。
①;
②;
③;
④
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
命题p:方程有两个不等的正实数根,命题q:方程无实数根.若“p且q”为真命题,求m的取值范围.
18.(本小题满分12分)
在对人们休闲的一次调查中,共调查了124人,其中女性70人,男性54人,女性中有43人主要的休闲方式是看电视,另外27人的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(I)根据以上数据建立一个2×2的列联表;
(Ⅱ)检验性别是否与休闲方式有关,可靠性有多大?
19.(本小题满分12分)
已知顶点是坐标原点,对称轴是x轴的抛物线经过点M().
(I)求抛物线的标准方程;
(Ⅱ)直线过点P(l,0),且与抛物线交于不同两点A,B,若=5,求直线的方程.
20.(本小题满分12分) 、
已知函数,a∈R
(I)若函数f(x)是R上的单调递增函数,求实数a的取值范围;
(Ⅱ)若是f(x)的一个极值点,求f(x)在R上的极大值与极小值.
21.(本小题满分13分)
已知直线:mx-2y+2m=O(m∈R)和椭圆,椭圆C的离心率为,连接椭圆的四个顶点形成四边形的面积为
(I)求椭圆C的方程,
(Ⅱ)记直线经过的定点为Q,过点Q作斜率为k的直线与椭圆C有两个不同的交点,求实数k的取值范围;
(Ⅲ)设直线与y轴的交点为P,M为椭圆C上的动点,线段PM长度的最大值为f(m),求f(m)的表达式.
22.(本小题满分13分)
函数
(I)如果函数g(x)单调减区调为(一,1),求函数g(x)解析式;
(Ⅱ)在(I)的条件下,求函数y=g(x)图彖过点p(1,1)的切线方程;
(Ⅲ)若,使关于x的不等式2f(x)≥(x)+2成立,求实数a取值范围.
同课章节目录
