2021-2022学年苏科新版九年级上册数学第3章数据的集中趋势和离散程度单元测试卷(word解析版)
文档属性
| 名称 | 2021-2022学年苏科新版九年级上册数学第3章数据的集中趋势和离散程度单元测试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 167.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 08:27:57 | ||
图片预览




文档简介
2021-2022学年苏科新版九年级上册数学《第3章
数据的集中趋势和离散程度》单元测试卷
一.选择题
1.某人上山的平均速度为3km/h,沿原路下山的平均速度为5km/h,上山用1h,则此人上下山的平均速度为( )
A.4km/h
B.3.75km/h
C.3.5km/h
D.4.5km/h
2.已知一组数据6,8,10,x的中位数与平均数相等,这样的x有( )
A.1个
B.2个
C.3个
D.4个以上(含4个)
3.在一次体检中,甲、乙、丙、丁四位同学的平均体重为52.5kg,而甲、乙、丙三位同学的平均体重为52.3kg.下列说法正确的是( )
A.四位同学体重的中位数一定是其中一位同学的体重
B.丁同学的体重一定高于其他三位同学的体重
C.丁同学的体重为53.1kg
D.四位同学体重的众数一定是52.5kg
4.某校在体育健康测试中,有8名男生“引体向上”的成绩(单位:次)分别是:14,12,8,9,16,12,7,10,这组数据的中位数和众数分别是( )
A.10,12
B.12,11
C.11,12
D.12,12
5.中小学时期是学生身心变化最为明显的时期,这个时期孩子们的身高变化呈现一定的趋势,7~15岁期间生子们会经历一个身高发育较迅速的阶段,我们把这个年龄阶段叫做生长速度峰值段,小明通过上网查阅《2016年某市儿童体格发育调查表》,了解某市男女生7~15岁身高平均值记录情况,并绘制了如下统计图,并得出以下结论:
①10岁之前,同龄的女生的平均身高一般会略高于男生的平均身高;
②10~12岁之间,女生达到生长速度峰值段,身高可能超过同龄男生;
③7~15岁期间,男生的平均身高始终高于女生的平均身高;
④13~15岁男生身高出现生长速度峰值段,男女生身高差距可能逐渐加大.
以上结论正确的是( )
A.①③
B.②③
C.②④
D.③④
6.小蓁与她的五位朋友参加保龄球比赛,如图为她们六人所得分数的盒状图.若小蓁所得到的分数恰为她们六人的平均分数,则小蓁得到多少分?( )
A.165
B.169
C.170
D.175
7.对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用max{a,b,c}表示这三个数中最大的数,例如:M;max{﹣1,2,3}=3,max
若M{4,x2,x+2}=max{4,x2,x+2};则x的值为( )
A.2或
B.2或﹣3
C.2
D.﹣3
8.若一组数据x1+1,x2+1,x3+1…xn+1的平均数为18,方差为2,则数据x1+2,x2+2,x3+2……,xn+2的平均数和方差分别是( )
A.18,2
B.19,3
C.19,2
D.20,4
二.填空题
9.五箱苹果的质量分别为(单位:千克)18,20,21,22,19.则这五箱苹果质量的平均数为
.
10.某生在一次考试中,语文、数学、英语三门学科的平均分为80分,物理、政治两科的平均分为85,则该生这5门学科的平均分为
分.
11.某校调查了20名男生某一周参加篮球运动次数,调查结果如表所示,那么这20名男生该周参加篮球运动次数的平均数是
次.
次数
2
3
4
5
人数
2
2
10
6
12.某学生7门学科考试成绩的总分是560分,其中3门学科的总分是234分,则另外4门学科成绩的平均分是
分.
13.在“手拉手,献爱心”捐款活动中,九年级七个班级的捐款数分别为:260、300、240、220、240、280、290(单位:元),则捐款数的中位数为
.
14.数据﹣1,2,2,3,5的中位数是
.
15.实数a,b满足|a﹣b|=5,则实数a,b的方差为
.
16.有11个正整数,平均数是10,中位数是9,众数只有一个8,问最大的正整数最大为
.
三.解答题
17.有甲、乙两个箱子,其中甲箱内有98颗球,分别标记号码1~98,且号码为不重复的整数,乙箱内没有球.已知小育从甲箱内拿出m颗球放入乙箱后,乙箱内球的号码的中位数为x.若此时甲箱内有a颗球的号码小于40,有b颗球的号码大于40,若他们的中位数都为x,求x的值.
18.已知10个数据的平均数是15,若对各个数据分别加上以下各数:1,0,﹣2,3,5,﹣3,6,9,5,﹣4.求所得新数据的平均数.
19.甲、乙两名运动员在6次百米跑训练中的成绩如下表:(单位:秒)
甲
10.8
10.9
11.0
10.7
11.2
10.8
乙
10.9
10.9
10.8
10.8
10.5
10.9
请你比较这两组数据的众数、平均数、中位数,并利用这些数据对甲、乙两名运动员进行评价?
20.某农贸市场经理为了了解两个不同产地的同一种蔬菜的销售情况,收集了九个省会城市的销售批发价格如下表(单位:元/克)
(1)哪个地方蔬菜批发价较高?
(2)若你是该经理,你将怎样做出经营计划?
产地
长沙
武汉
广州
海口
福州
昆明
南宁
南京
郑州
甲
0.85
0.83
0.90
0.90
0.88
0.86
0.82
0.95
0.84
乙
0.80
0.82
0.95
0.97
0.86
0.82
0.83
0.84
0.80
21.某单位需招聘一名技术员,对甲、乙、丙三名候选人进行了笔试和面试两项测试,其成绩如下表所示:
根据录用程序,该单位又组织了100名评议人员对三人进行投票测评,其得票率如扇形图所示,每票1分(没有弃权票.每人只能投1票)
测试项目
测试成绩/分
甲
乙
丙
笔试
80
85
95
面试
98
75
73
(1)请算出三人的民主评议得分;
(2)该单位将笔试、面试、民主评议三项测试得分按2:2:1确定综合成绩,谁将被录用?请说明理由.
22.某书店一本数学辅导书的售价与客户的订购数量的关系如下表:
订购数量x(单位:本)
1≤x≤50
51≤x≤100
x>100
每本售价y(单位:元)
15
14
13
请根据以上信息回答下列问题:
(1)订购50本书和订购53本书相比,哪种订购方式所需总费用更少?
(2)该出版社将8所学校的订购情况记录如下:80本,75本,70本,80本,85本,90本,50本,400本.这本书在以上8所学校中销售量的中位数是多少?
(3)请你帮出版社计算一下这本书在以上8所学校中的平均售价?
23.一果品商店对A,B,C,D,E,F这六种果品的售价进行了调整,并计算了这六种果品调价前后售价的平均数、中位数和众数,如下表所示:
果品种类
A
B
C
D
E
F
平均数
中位数
众数
调整前售价(元/千克)
3
3
5
7
9
12
6.5
6
n
调整后售价(元/千克)
2
2
4
7
10
14
6.5
m
2
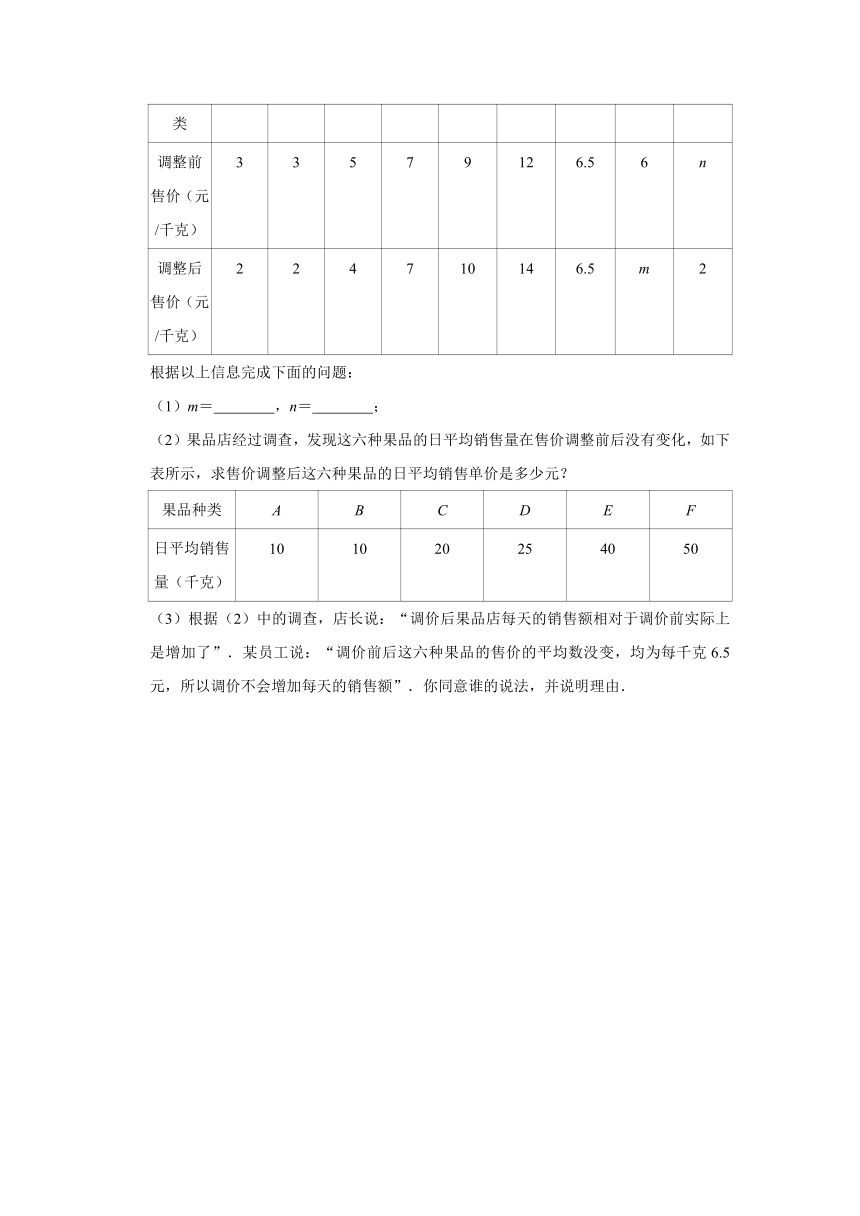
根据以上信息完成下面的问题:
(1)m=
,n=
;
(2)果品店经过调查,发现这六种果品的日平均销售量在售价调整前后没有变化,如下表所示,求售价调整后这六种果品的日平均销售单价是多少元?
果品种类
A
B
C
D
E
F
日平均销售量(千克)
10
10
20
25
40
50
(3)根据(2)中的调查,店长说:“调价后果品店每天的销售额相对于调价前实际上是增加了”.某员工说:“调价前后这六种果品的售价的平均数没变,均为每千克6.5元,所以调价不会增加每天的销售额”.你同意谁的说法,并说明理由.
参考答案与试题解析
一.选择题
1.解:根据题意得,路程s=上山的平均速度v1×上山时间t1=3km/h×1h=3km,
∴下山时间t2===0.6h,
∴平均速度v==3.75km/h,
故选:B.
2.解:(1)将这组数据从大到小的顺序排列为10,8,x,6,
处于中间位置的数是8,x,
那么由中位数的定义可知,这组数据的中位数是(8+x)÷2,
平均数为(10+8+x+6)÷4,
∵数据10,8,x,6,的中位数与平均数相等,
∴(8+x)÷2=(10+8+x+6)÷4,
解得x=8,大小位置与8对调,不影响结果,符合题意;
(2)将这组数据从大到小的顺序排列后10,8,6,x,
中位数是(8+6)÷2=7,
此时平均数是(10+8+x+6)÷4=7,
解得x=4,符合排列顺序;
(3)将这组数据从大到小的顺序排列后x,10,8,6,
中位数是(10+8)÷2=9,
平均数(10+8+x+6)÷4=9,
解得x=12,符合排列顺序.
∴x的值为4、8或12.
故选:C.
3.解:A、四位同学体重的中位数一定是其中两位同学的体重的平均数,本选项说法错误;
B、丁同学的体重一定高于其他三位同学的体重的平均数,但不一定高于其他三位同学的体重,本选项说法错误;
C、设丁同学的体重为xkg,
由题意得,=52.5,
解得,x=53.1,
∴丁同学的体重为53.1kg,本选项说法正确;
D、四位同学体重的众数不一定是52.5kg,本选项说法错误;
故选:C.
4.解:原数据按由小到大排列为:7,8,9,10,12,12,14,16,
所以这组数据的中位数=(10+12)=11,
众数为12.
故选:C.
5.解:①10岁之前,同龄的女生的平均身高与男生的平均身高基本相同,故该说法错误;
②10~12岁之间,女生达到生长速度峰值段,身高可能超过同龄男生,故该说法正确;
③7~15岁期间,男生的平均身高不一定高于女生的平均身高,如11岁的男生的平均身高低于女生的平均身高,故该说法错误;
④13~15岁男生身高出现生长速度峰值段,男女生身高差距可能逐渐加大,故该说法正确.
故选:C.
6.解:设小蓁得到x分,根据题意得:
(120+145+175+195+210+x)÷6=x,
解得:x=169,
答:小蓁得到169分;
故选:B.
7.解:解法一:观察选项,发现3个有2,故先令x=2,
则M{4,x2,x+2}==4,max{4,x2,x+2}=max{4,4,4}=4
故x=2符合题意,排除D;
令x=,则M{4,x2,x+2}==<4
故x=不符合题意,排除A;
令x=﹣3,则M{4,x2,x+2}==4,max{4,x2,x+2}=max{4,9,﹣1}=9
4<9,故x=﹣3不符合题意,排除B;
解法二:∵M{4,x2,x+2}=max{4,x2,x+2},
∴4=x2=x+2,
解得x=2.
综上,故选:C.
8.解:∵数据x1+1,x2+1,x3+1…xn+1的平均数为18,
∴数据x1+2,x2+2,x3+2……,xn+2的平均数为18+1=19;
∵数据x1+1,x2+1,x3+1…xn+1的方差是2,
∴数据x1+2,x2+2,x3+2……,xn+2的方差是2;
故选:C.
二.填空题
9.解:这五箱苹果质量的平均数为:=20.
故答案为:20.
10.解:由题意知,语文、数学、英语三门学科的总分=3×80=240,物理、政治两科的总分=85×2=170,
∴该生这5门学科的平均分=(240+170)÷5=410÷5=82(分).
故填82.
11.解:(2×2+3×2+4×10+5×6)÷20
=(4+6+40+30)÷20
=80÷20
=4(次).
∴这20名男生该周参加篮球运动次数的平均数是4次.
故答案为:4.
12.解:另外4门学科成绩的平均分=(560﹣234)÷4=81.5.
故填81.5.
13.解:从小到大数据排列为220,240,240,260,280,290,300,共7个数,
第4个数是260,故中位数是260.
故答案为:260.
14.解:将这5个数据重新排列为﹣1,2,2,3,5,
所以这组数据的中位数是2,
故答案为:2.
15.解:若a>b,则b=a﹣5,
∴==a﹣,
∴S2=
[(a﹣a+)2+(a﹣5﹣a+)2]=×(+)=6.25;
若a<b,则b=a+5,
同理可得,S2=6.25;
故答案为:6.25
16.解:∵11个正整数,平均数是10,
∴和为110,
∵中位数是9,众数只有一个8,
∴当11个正整数为1,1,8,8,8,9,9,10,10,11,35时,最大的正整数最大为35,
故答案为:35.
三.解答题
17.解:因为他们的中位数都为x,所以甲、乙箱内球的数量应该都是偶数,
设在甲箱内球的号码小于x的数量是c颗,则大于x的数量也是c颗;
设在乙箱内球的号码小于x数量是d颗,则大于x数量也是d颗,
于是在全部98颗球中,号码小于x数量是(c+d)颗,大于x数量也是(c+d)颗,即1~98的中位数是x,
∴x=(49+50)=49.5.
18.解:所有数据的和为15×10+[1+0+(﹣2)+3+5+(﹣3)+6+9+5+(﹣4)]=160,
所以所得新数据的平均数=160÷10=16.
19.解:甲:数据10.8出现2次,次数最多,所以众数是10.8;
平均数=(10.8+10.9+11.0+10.7+11.2+10.8)÷6=10.9;
中位数=(10.8+10.9)÷2=10.85;
乙:数据10.9出现3次,次数最多,所以众数为10.9;
平均数=(10.9+10.9+10.8+10.8+10.5+10.9)÷6=10.8;
中位数=(10.8+10.9)÷2=10.85;
所以从众数上看,乙的整体成绩差于甲的整体成绩;
从平均数上看,乙的平均成绩优于甲的平均成绩;
从中位数看,甲、乙的成绩一样好.
20.解:(1)由图可得甲的批发价的平均数为:0.87元,乙的批发价的平均数约为:0.85元
∴甲地方蔬菜批发价高.
(2)若进货则选乙地蔬菜,若经营批发业务则选甲地的蔬菜.
21.解:(1)甲民主评议得分:100×25%=25分;
乙民主评议得分:100×40%=40分;
丙民主评议得分:100×35%=35分;
(2)甲的成绩:80×+98×+25×=76.2分;
乙的成绩:85×+75×+40×=72分;
丙的成绩:95×+73×+35×=74.2分.
∴甲将被录用,因为甲的成绩最好.
22.解:(1)订购50本书的费用为50×15=750元,
订购53本书的费用为53×14=742元,
所以订购53本书的总费用更少;
(2)∵数据从小到大排列:50,70,75,80,80,85,90,400,
∴中位数=(80+80)÷2=80,
∴这本书在以上8所学校中销售量的中位数是80(本);
(3)8所学校的平均售价为:
[50×15+(80+75+70+80+85+90)×14+400×13]÷930=12670÷930≈13.6(元),
∴每本书的平均售价为13.6元.
23.解:(1)数据2,2,4,7,10,14的中位数m为:=5.5;
数据3,3,5,7,9,12的众数n为3;
故答案为:5.5,3;
(2)售价调整后这六种果品的日平均销售单价是:
(2×10+2×10+4×20+7×25+10×40+14×50)÷(10+10+20+25+40+50)=1395÷155=9(元/千克);
(3)同意店长的说法.
理由:调价前的日平均收入为:
3×10+3×10+5×20+7×25+9×40+12×50=1295(元);
调价后的日平均收入为:
2×10+2×10+4×20+7×25+10×40+14×50=1395(元),
∵1395>1295,
∴店长的说法正确.
数据的集中趋势和离散程度》单元测试卷
一.选择题
1.某人上山的平均速度为3km/h,沿原路下山的平均速度为5km/h,上山用1h,则此人上下山的平均速度为( )
A.4km/h
B.3.75km/h
C.3.5km/h
D.4.5km/h
2.已知一组数据6,8,10,x的中位数与平均数相等,这样的x有( )
A.1个
B.2个
C.3个
D.4个以上(含4个)
3.在一次体检中,甲、乙、丙、丁四位同学的平均体重为52.5kg,而甲、乙、丙三位同学的平均体重为52.3kg.下列说法正确的是( )
A.四位同学体重的中位数一定是其中一位同学的体重
B.丁同学的体重一定高于其他三位同学的体重
C.丁同学的体重为53.1kg
D.四位同学体重的众数一定是52.5kg
4.某校在体育健康测试中,有8名男生“引体向上”的成绩(单位:次)分别是:14,12,8,9,16,12,7,10,这组数据的中位数和众数分别是( )
A.10,12
B.12,11
C.11,12
D.12,12
5.中小学时期是学生身心变化最为明显的时期,这个时期孩子们的身高变化呈现一定的趋势,7~15岁期间生子们会经历一个身高发育较迅速的阶段,我们把这个年龄阶段叫做生长速度峰值段,小明通过上网查阅《2016年某市儿童体格发育调查表》,了解某市男女生7~15岁身高平均值记录情况,并绘制了如下统计图,并得出以下结论:
①10岁之前,同龄的女生的平均身高一般会略高于男生的平均身高;
②10~12岁之间,女生达到生长速度峰值段,身高可能超过同龄男生;
③7~15岁期间,男生的平均身高始终高于女生的平均身高;
④13~15岁男生身高出现生长速度峰值段,男女生身高差距可能逐渐加大.
以上结论正确的是( )
A.①③
B.②③
C.②④
D.③④
6.小蓁与她的五位朋友参加保龄球比赛,如图为她们六人所得分数的盒状图.若小蓁所得到的分数恰为她们六人的平均分数,则小蓁得到多少分?( )
A.165
B.169
C.170
D.175
7.对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用max{a,b,c}表示这三个数中最大的数,例如:M;max{﹣1,2,3}=3,max
若M{4,x2,x+2}=max{4,x2,x+2};则x的值为( )
A.2或
B.2或﹣3
C.2
D.﹣3
8.若一组数据x1+1,x2+1,x3+1…xn+1的平均数为18,方差为2,则数据x1+2,x2+2,x3+2……,xn+2的平均数和方差分别是( )
A.18,2
B.19,3
C.19,2
D.20,4
二.填空题
9.五箱苹果的质量分别为(单位:千克)18,20,21,22,19.则这五箱苹果质量的平均数为
.
10.某生在一次考试中,语文、数学、英语三门学科的平均分为80分,物理、政治两科的平均分为85,则该生这5门学科的平均分为
分.
11.某校调查了20名男生某一周参加篮球运动次数,调查结果如表所示,那么这20名男生该周参加篮球运动次数的平均数是
次.
次数
2
3
4
5
人数
2
2
10
6
12.某学生7门学科考试成绩的总分是560分,其中3门学科的总分是234分,则另外4门学科成绩的平均分是
分.
13.在“手拉手,献爱心”捐款活动中,九年级七个班级的捐款数分别为:260、300、240、220、240、280、290(单位:元),则捐款数的中位数为
.
14.数据﹣1,2,2,3,5的中位数是
.
15.实数a,b满足|a﹣b|=5,则实数a,b的方差为
.
16.有11个正整数,平均数是10,中位数是9,众数只有一个8,问最大的正整数最大为
.
三.解答题
17.有甲、乙两个箱子,其中甲箱内有98颗球,分别标记号码1~98,且号码为不重复的整数,乙箱内没有球.已知小育从甲箱内拿出m颗球放入乙箱后,乙箱内球的号码的中位数为x.若此时甲箱内有a颗球的号码小于40,有b颗球的号码大于40,若他们的中位数都为x,求x的值.
18.已知10个数据的平均数是15,若对各个数据分别加上以下各数:1,0,﹣2,3,5,﹣3,6,9,5,﹣4.求所得新数据的平均数.
19.甲、乙两名运动员在6次百米跑训练中的成绩如下表:(单位:秒)
甲
10.8
10.9
11.0
10.7
11.2
10.8
乙
10.9
10.9
10.8
10.8
10.5
10.9
请你比较这两组数据的众数、平均数、中位数,并利用这些数据对甲、乙两名运动员进行评价?
20.某农贸市场经理为了了解两个不同产地的同一种蔬菜的销售情况,收集了九个省会城市的销售批发价格如下表(单位:元/克)
(1)哪个地方蔬菜批发价较高?
(2)若你是该经理,你将怎样做出经营计划?
产地
长沙
武汉
广州
海口
福州
昆明
南宁
南京
郑州
甲
0.85
0.83
0.90
0.90
0.88
0.86
0.82
0.95
0.84
乙
0.80
0.82
0.95
0.97
0.86
0.82
0.83
0.84
0.80
21.某单位需招聘一名技术员,对甲、乙、丙三名候选人进行了笔试和面试两项测试,其成绩如下表所示:
根据录用程序,该单位又组织了100名评议人员对三人进行投票测评,其得票率如扇形图所示,每票1分(没有弃权票.每人只能投1票)
测试项目
测试成绩/分
甲
乙
丙
笔试
80
85
95
面试
98
75
73
(1)请算出三人的民主评议得分;
(2)该单位将笔试、面试、民主评议三项测试得分按2:2:1确定综合成绩,谁将被录用?请说明理由.
22.某书店一本数学辅导书的售价与客户的订购数量的关系如下表:
订购数量x(单位:本)
1≤x≤50
51≤x≤100
x>100
每本售价y(单位:元)
15
14
13
请根据以上信息回答下列问题:
(1)订购50本书和订购53本书相比,哪种订购方式所需总费用更少?
(2)该出版社将8所学校的订购情况记录如下:80本,75本,70本,80本,85本,90本,50本,400本.这本书在以上8所学校中销售量的中位数是多少?
(3)请你帮出版社计算一下这本书在以上8所学校中的平均售价?
23.一果品商店对A,B,C,D,E,F这六种果品的售价进行了调整,并计算了这六种果品调价前后售价的平均数、中位数和众数,如下表所示:
果品种类
A
B
C
D
E
F
平均数
中位数
众数
调整前售价(元/千克)
3
3
5
7
9
12
6.5
6
n
调整后售价(元/千克)
2
2
4
7
10
14
6.5
m
2
根据以上信息完成下面的问题:
(1)m=
,n=
;
(2)果品店经过调查,发现这六种果品的日平均销售量在售价调整前后没有变化,如下表所示,求售价调整后这六种果品的日平均销售单价是多少元?
果品种类
A
B
C
D
E
F
日平均销售量(千克)
10
10
20
25
40
50
(3)根据(2)中的调查,店长说:“调价后果品店每天的销售额相对于调价前实际上是增加了”.某员工说:“调价前后这六种果品的售价的平均数没变,均为每千克6.5元,所以调价不会增加每天的销售额”.你同意谁的说法,并说明理由.
参考答案与试题解析
一.选择题
1.解:根据题意得,路程s=上山的平均速度v1×上山时间t1=3km/h×1h=3km,
∴下山时间t2===0.6h,
∴平均速度v==3.75km/h,
故选:B.
2.解:(1)将这组数据从大到小的顺序排列为10,8,x,6,
处于中间位置的数是8,x,
那么由中位数的定义可知,这组数据的中位数是(8+x)÷2,
平均数为(10+8+x+6)÷4,
∵数据10,8,x,6,的中位数与平均数相等,
∴(8+x)÷2=(10+8+x+6)÷4,
解得x=8,大小位置与8对调,不影响结果,符合题意;
(2)将这组数据从大到小的顺序排列后10,8,6,x,
中位数是(8+6)÷2=7,
此时平均数是(10+8+x+6)÷4=7,
解得x=4,符合排列顺序;
(3)将这组数据从大到小的顺序排列后x,10,8,6,
中位数是(10+8)÷2=9,
平均数(10+8+x+6)÷4=9,
解得x=12,符合排列顺序.
∴x的值为4、8或12.
故选:C.
3.解:A、四位同学体重的中位数一定是其中两位同学的体重的平均数,本选项说法错误;
B、丁同学的体重一定高于其他三位同学的体重的平均数,但不一定高于其他三位同学的体重,本选项说法错误;
C、设丁同学的体重为xkg,
由题意得,=52.5,
解得,x=53.1,
∴丁同学的体重为53.1kg,本选项说法正确;
D、四位同学体重的众数不一定是52.5kg,本选项说法错误;
故选:C.
4.解:原数据按由小到大排列为:7,8,9,10,12,12,14,16,
所以这组数据的中位数=(10+12)=11,
众数为12.
故选:C.
5.解:①10岁之前,同龄的女生的平均身高与男生的平均身高基本相同,故该说法错误;
②10~12岁之间,女生达到生长速度峰值段,身高可能超过同龄男生,故该说法正确;
③7~15岁期间,男生的平均身高不一定高于女生的平均身高,如11岁的男生的平均身高低于女生的平均身高,故该说法错误;
④13~15岁男生身高出现生长速度峰值段,男女生身高差距可能逐渐加大,故该说法正确.
故选:C.
6.解:设小蓁得到x分,根据题意得:
(120+145+175+195+210+x)÷6=x,
解得:x=169,
答:小蓁得到169分;
故选:B.
7.解:解法一:观察选项,发现3个有2,故先令x=2,
则M{4,x2,x+2}==4,max{4,x2,x+2}=max{4,4,4}=4
故x=2符合题意,排除D;
令x=,则M{4,x2,x+2}==<4
故x=不符合题意,排除A;
令x=﹣3,则M{4,x2,x+2}==4,max{4,x2,x+2}=max{4,9,﹣1}=9
4<9,故x=﹣3不符合题意,排除B;
解法二:∵M{4,x2,x+2}=max{4,x2,x+2},
∴4=x2=x+2,
解得x=2.
综上,故选:C.
8.解:∵数据x1+1,x2+1,x3+1…xn+1的平均数为18,
∴数据x1+2,x2+2,x3+2……,xn+2的平均数为18+1=19;
∵数据x1+1,x2+1,x3+1…xn+1的方差是2,
∴数据x1+2,x2+2,x3+2……,xn+2的方差是2;
故选:C.
二.填空题
9.解:这五箱苹果质量的平均数为:=20.
故答案为:20.
10.解:由题意知,语文、数学、英语三门学科的总分=3×80=240,物理、政治两科的总分=85×2=170,
∴该生这5门学科的平均分=(240+170)÷5=410÷5=82(分).
故填82.
11.解:(2×2+3×2+4×10+5×6)÷20
=(4+6+40+30)÷20
=80÷20
=4(次).
∴这20名男生该周参加篮球运动次数的平均数是4次.
故答案为:4.
12.解:另外4门学科成绩的平均分=(560﹣234)÷4=81.5.
故填81.5.
13.解:从小到大数据排列为220,240,240,260,280,290,300,共7个数,
第4个数是260,故中位数是260.
故答案为:260.
14.解:将这5个数据重新排列为﹣1,2,2,3,5,
所以这组数据的中位数是2,
故答案为:2.
15.解:若a>b,则b=a﹣5,
∴==a﹣,
∴S2=
[(a﹣a+)2+(a﹣5﹣a+)2]=×(+)=6.25;
若a<b,则b=a+5,
同理可得,S2=6.25;
故答案为:6.25
16.解:∵11个正整数,平均数是10,
∴和为110,
∵中位数是9,众数只有一个8,
∴当11个正整数为1,1,8,8,8,9,9,10,10,11,35时,最大的正整数最大为35,
故答案为:35.
三.解答题
17.解:因为他们的中位数都为x,所以甲、乙箱内球的数量应该都是偶数,
设在甲箱内球的号码小于x的数量是c颗,则大于x的数量也是c颗;
设在乙箱内球的号码小于x数量是d颗,则大于x数量也是d颗,
于是在全部98颗球中,号码小于x数量是(c+d)颗,大于x数量也是(c+d)颗,即1~98的中位数是x,
∴x=(49+50)=49.5.
18.解:所有数据的和为15×10+[1+0+(﹣2)+3+5+(﹣3)+6+9+5+(﹣4)]=160,
所以所得新数据的平均数=160÷10=16.
19.解:甲:数据10.8出现2次,次数最多,所以众数是10.8;
平均数=(10.8+10.9+11.0+10.7+11.2+10.8)÷6=10.9;
中位数=(10.8+10.9)÷2=10.85;
乙:数据10.9出现3次,次数最多,所以众数为10.9;
平均数=(10.9+10.9+10.8+10.8+10.5+10.9)÷6=10.8;
中位数=(10.8+10.9)÷2=10.85;
所以从众数上看,乙的整体成绩差于甲的整体成绩;
从平均数上看,乙的平均成绩优于甲的平均成绩;
从中位数看,甲、乙的成绩一样好.
20.解:(1)由图可得甲的批发价的平均数为:0.87元,乙的批发价的平均数约为:0.85元
∴甲地方蔬菜批发价高.
(2)若进货则选乙地蔬菜,若经营批发业务则选甲地的蔬菜.
21.解:(1)甲民主评议得分:100×25%=25分;
乙民主评议得分:100×40%=40分;
丙民主评议得分:100×35%=35分;
(2)甲的成绩:80×+98×+25×=76.2分;
乙的成绩:85×+75×+40×=72分;
丙的成绩:95×+73×+35×=74.2分.
∴甲将被录用,因为甲的成绩最好.
22.解:(1)订购50本书的费用为50×15=750元,
订购53本书的费用为53×14=742元,
所以订购53本书的总费用更少;
(2)∵数据从小到大排列:50,70,75,80,80,85,90,400,
∴中位数=(80+80)÷2=80,
∴这本书在以上8所学校中销售量的中位数是80(本);
(3)8所学校的平均售价为:
[50×15+(80+75+70+80+85+90)×14+400×13]÷930=12670÷930≈13.6(元),
∴每本书的平均售价为13.6元.
23.解:(1)数据2,2,4,7,10,14的中位数m为:=5.5;
数据3,3,5,7,9,12的众数n为3;
故答案为:5.5,3;
(2)售价调整后这六种果品的日平均销售单价是:
(2×10+2×10+4×20+7×25+10×40+14×50)÷(10+10+20+25+40+50)=1395÷155=9(元/千克);
(3)同意店长的说法.
理由:调价前的日平均收入为:
3×10+3×10+5×20+7×25+9×40+12×50=1295(元);
调价后的日平均收入为:
2×10+2×10+4×20+7×25+10×40+14×50=1395(元),
∵1395>1295,
∴店长的说法正确.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
