2021-2022学年鲁教版九年级数学上册2.4解直角三角形 同步能力提升训练 (word版、含解析)
文档属性
| 名称 | 2021-2022学年鲁教版九年级数学上册2.4解直角三角形 同步能力提升训练 (word版、含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 513.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 00:00:00 | ||
图片预览


文档简介
2021-2022学年鲁教版九年级数学上册《2.4解直角三角形》同步能力提升训练(附答案)
一、选择题
1.如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD,若AB=2BD,tan∠BCD=,则的值为( )
A.1
B.2
C.
D.
2.如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( )
A.
B.2
C.
D.
3.如图小张同学的尺规作图步骤,其具体做法如下:
①在射线AD上顺次截取AB=BC=a,②分别以B、C为圆心,以a为半径作圆弧,两弧交于点E,③连接AE、BE、CE,则下列说法错误的是( )
A.△BCE为等边三角形
B.△ACE的面积为
C.
D.∠AEC=3∠A
4.如图,在四边形ABCD中,∠ACB=∠CAD=90°,AC=CB,sin∠ACD=,则tan∠BDC的值是( )
A.
B.
C.
D.
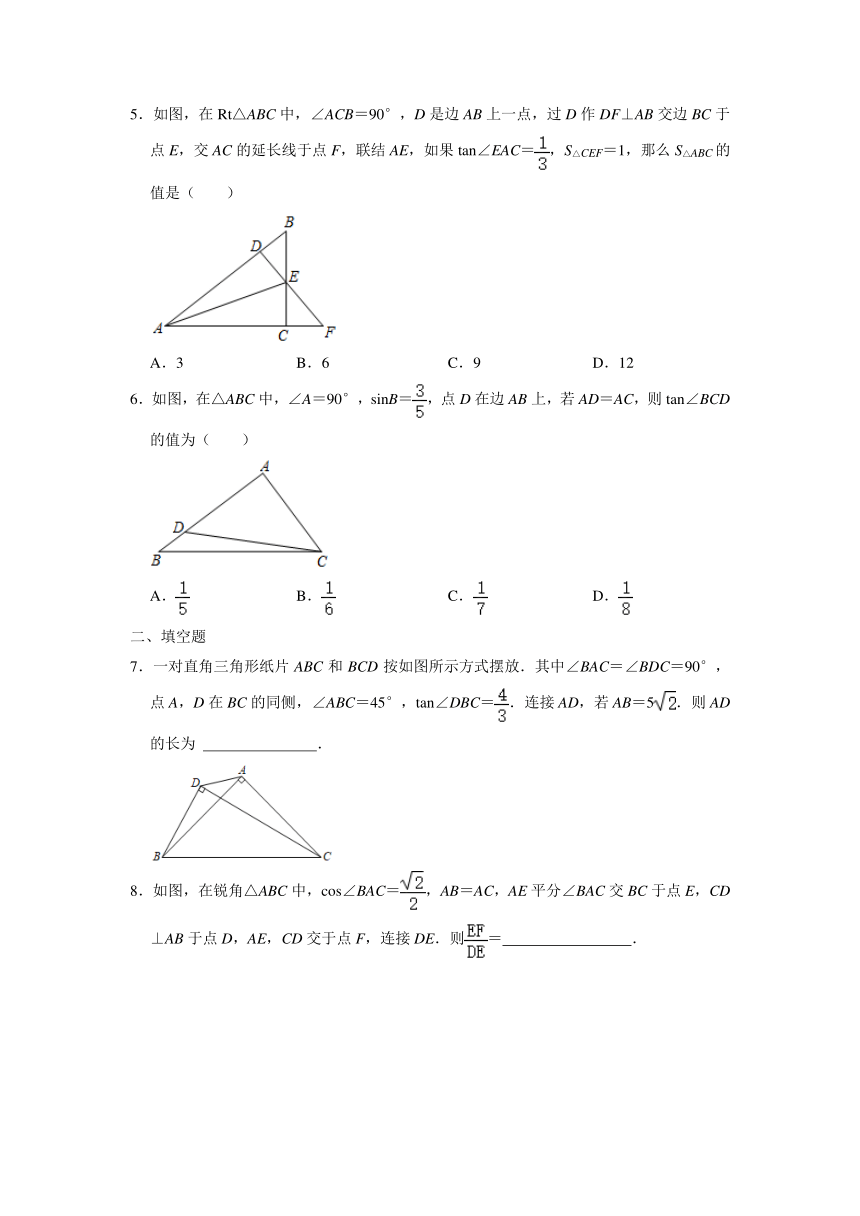
5.如图,在Rt△ABC中,∠ACB=90°,D是边AB上一点,过D作DF⊥AB交边BC于点E,交AC的延长线于点F,联结AE,如果tan∠EAC=,S△CEF=1,那么S△ABC的值是( )
A.3
B.6
C.9
D.12
6.如图,在△ABC中,∠A=90°,sinB=,点D在边AB上,若AD=AC,则tan∠BCD的值为( )
A.
B.
C.
D.
二、填空题
7.一对直角三角形纸片ABC和BCD按如图所示方式摆放.其中∠BAC=∠BDC=90°,点A,D在BC的同侧,∠ABC=45°,tan∠DBC=.连接AD,若AB=5.则AD的长为
.
8.如图,在锐角△ABC中,cos∠BAC=,AB=AC,AE平分∠BAC交BC于点E,CD⊥AB于点D,AE,CD交于点F,连接DE.则=
.
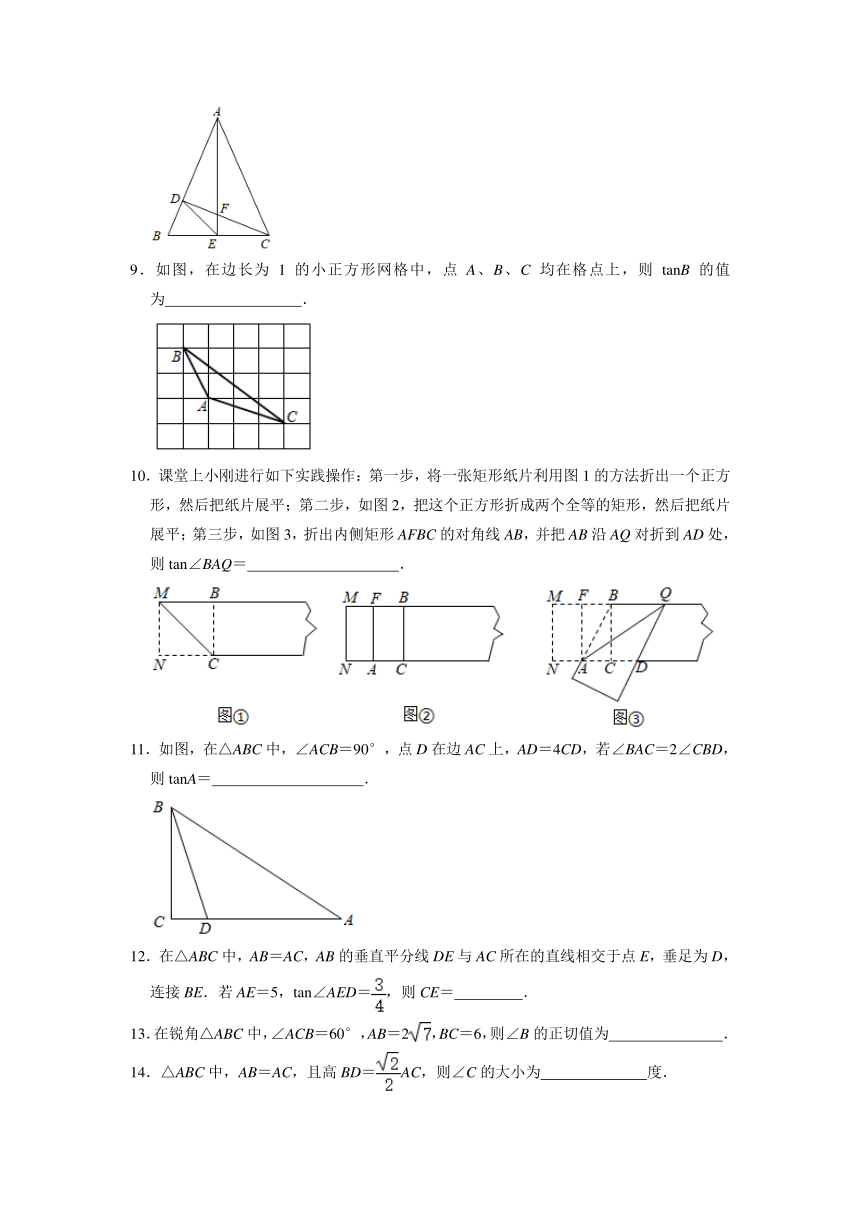
9.如图,在边长为1的小正方形网格中,点A、B、C均在格点上,则tanB的值为
.
10.课堂上小刚进行如下实践操作:第一步,将一张矩形纸片利用图1的方法折出一个正方形,然后把纸片展平;第二步,如图2,把这个正方形折成两个全等的矩形,然后把纸片展平;第三步,如图3,折出内侧矩形AFBC的对角线AB,并把AB沿AQ对折到AD处,则tan∠BAQ=
.
11.如图,在△ABC中,∠ACB=90°,点D在边AC上,AD=4CD,若∠BAC=2∠CBD,则tanA=
.
12.在△ABC中,AB=AC,AB的垂直平分线DE与AC所在的直线相交于点E,垂足为D,连接BE.若AE=5,tan∠AED=,则CE=
.
13.在锐角△ABC中,∠ACB=60°,AB=2,BC=6,则∠B的正切值为
.
14.△ABC中,AB=AC,且高BD=AC,则∠C的大小为
度.
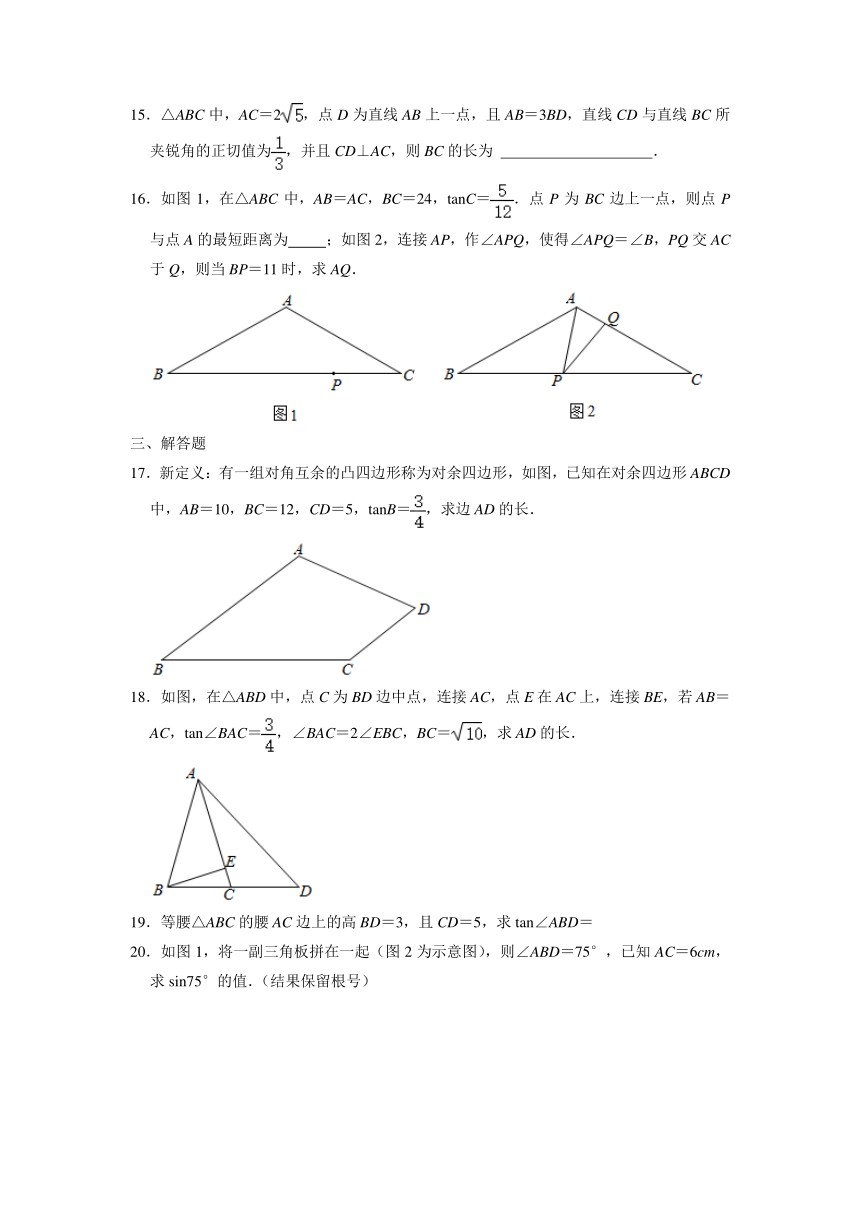
15.△ABC中,AC=2,点D为直线AB上一点,且AB=3BD,直线CD与直线BC所夹锐角的正切值为,并且CD⊥AC,则BC的长为
.
16.如图1,在△ABC中,AB=AC,BC=24,tanC=.点P为BC边上一点,则点P与点A的最短距离为
;如图2,连接AP,作∠APQ,使得∠APQ=∠B,PQ交AC于Q,则当BP=11时,求AQ.
三、解答题
17.新定义:有一组对角互余的凸四边形称为对余四边形,如图,已知在对余四边形ABCD中,AB=10,BC=12,CD=5,tanB=,求边AD的长.
18.如图,在△ABD中,点C为BD边中点,连接AC,点E在AC上,连接BE,若AB=AC,tan∠BAC=,∠BAC=2∠EBC,BC=,求AD的长.
19.等腰△ABC的腰AC边上的高BD=3,且CD=5,求tan∠ABD=
20.如图1,将一副三角板拼在一起(图2为示意图),则∠ABD=75°,已知AC=6cm,求sin75°的值.(结果保留根号)
参考答案
1.解:过点D作DM⊥BC,交CB的延长线于点M,
∵∠ACB=∠DMB=90°,∠ABC=∠DBM,
∴△ABC∽△DBM,
∴==,
∵AB=2BD,
∴===,
在Rt△CDM中,
由于tan∠MCD==,设DM=2k,则CM=3k,
又∵==,
∴BC=2k,AC=4k,
∴==2,
故选:B.
2.解:如图:
作OF⊥AB于F,
∵AB=AC,AD平分∠BAC.
∴∠ODB=90°.BD=CD=6.
∴根据勾股定理得:AD==8.
∵BE平分∠ABC.
∴OF=OD,BF=BD=6,AF=10﹣6=4.
设OD=OF=x,则AO=8﹣x,在Rt△AOF中,根据勾股定理得:
(8﹣x)2=x2+42.
∴x=3.
∴OD=3.
在Rt△OBD中,tan∠OBD===.
故选:A.
3.解:由题意得AB=BC=BE=CE=a,
∴△BCE为等边三角形,故A选项正确.
∴△BCE的面积为,故B选项错误.
∵BE=BA,∠EBC=60°,
∴∠A=∠BEA=30°,
∴sinA=sin30°=,故C选项正确.
∴∠AEC=∠BEA+∠BEC=30°+60°=90°,
∴∠AEC=3∠A,故D选项正确.
故选:B.
4.解:如图,过点D作DE⊥BC交BC的延长线于E,过点C作CH⊥BD于H.
∵∠ACB=∠CAD=90°,DE⊥EC,
∴∠ACE=∠E=90°,
∴四边形ACED是矩形,
∴AD=CE,AC=DE,
∵sin∠ACD==,
∴可以假设AD=3k,CD=5k,则AC=BC=DE=4k,
∴BE=BC+CE=7k,
∴BD===k,
∵S△CBD= BC DE= BD CH,
∴CH=k,
∴DH===k,
∴tan∠BDC==.
方法二:过点B作BH垂于DC交DC的延长线于点H,
设AD=3k,CD=5k,则AC=BC=4k,
∵∠H=∠CAD=∠ACB=90°,
∴∠ACD+∠BCH=90°,∠CBH+∠BCH=90°,
∴∠ACD=∠CBH,
∴△CBH∽△DCA,
∴==,
∴==,
∴BH=k,CH=k,
∴DH=CH+CD=k+5k=k,
tan∠BDC==.
故选:C.
5.解:∵∠ACB=90°,
∴∠BAC+∠B=90°,
又∵DF⊥AB,
∴∠ADF=90°,
∴∠BAC+∠F=90°,
∴∠B=∠F,
又∵∠ECF=∠ACB=90°,
∴△ECF∽△ACB,
∴==tan∠EAC=,
∴=,
又∵S△ECF=1,
∴S△ABC=9,
故选:C.
6.解:如图,作DH⊥BC于H.
∵∠A=90°,sinB==,
∴可以假设AC=3k,BC=5k,则AB=4k,
∵AC=AD=3k,
∴BD=k,
∵∠B=∠B,∠DHB=∠A=90°,
∴△BHD∽△BAC,
∴==,
∴==,
∴DH=k,BH=k,
∵CH=BC﹣BH=5k﹣k=k,
∴tan∠BCD===,
故选:C.
7.解:如图,分别过点A、D作AF⊥BC、DE⊥BC,交BC于点F、E,过点D作DM⊥AF,于点M,
在Rt△ABC中,
∵AB=5,∠ABC=45°,
∴AC=AB=5,BC=10,
∴AF=BF=5,
在Rt△BCD中,
∵tan∠DBC=,
∴BD=6,
在Rt△BDE中,
∵tan∠DBE=,
∴DE=,BE=,
∵∠DEF=∠DMF=∠EFM=90°,
∴四边形DEFM是矩形,
∴DM=EF=BF﹣BE=,MF=DE=,
∴AM=AF﹣MF=,
在Rt△ADM中,由勾股定理,得:AD==,
故答案为:.
8.解:如图,在AE上取一点M,使得AM=MC.设EC=m.
∵cos∠BAC=,
∴∠BAC=45°,
∵AB=AC,AE平分∠BAC,
∴AE⊥BC,∠EAC=∠BAC=22.5°,
∵MA=MC,
∴∠MAC=∠MCA=22.5°,
∴∠CME=∠MAC+∠MCA=45°,
∴EC=EM=m,AM=CM=m,AE=m+m,
∵∠ADC=∠AEC=90°,
∴A,D,E,C四点共圆,
∴∠ECF=∠DAE=22.5°,
∵∠DAE=∠EAC,
∴=,
∴DE=ED,
∴===tan22.5°==﹣1.
故答案为:﹣1
9.解:如图,取格点E,连接AE,EC,则B,A,E共线,∠E=90°.
∵EC==,BE==2,
∴tanB==.
故答案为:.
10.解:过点Q作QH⊥AD,垂足为H,
由折叠可知,∠BAQ=∠QAH,AB=AD,
又∵MQ∥NH,
∴∠QAH=∠BQA,
∴∠BAQ=∠BQA,
∴AB=BQ,
∴四边形ADQB是菱形,
∴AB=QD,
又∵BC=QH,
∴△ABC≌△DQH
(HL),
∴AC=DH,
设AC=a=DH,则BC=2a=QH,
∴AB==a,
∴AH=a+a=(+1)a,
在Rt△AQH中,tan∠QAH===.
即tan∠BAQ=tan∠QAH=.
11.解:延长AC至E,使CE=CD,连接BE,
∵∠ACB=90°,
∴BC⊥AC,
∵CE=CD,
∴BC是DE的垂直平分线,
∴BD=BE,
∴∠E=∠BDE,
设∠CBD=α,则∠BAC=2α,
∴∠E=∠BDE=90°﹣α,
∴∠ABE=180°﹣∠E﹣BAC=180°﹣(90°﹣α)﹣2α=90°﹣α,
∴∠E=∠ABE,
∴AB=AE,
设CD=x,则AD=4x,
∴AE=AB=6x,AC=5x,
在Rt△ABC中,BC===x,
∴tanA==.
故答案为:.
12.解:分两种情形:
当DE与AC边相交时,如图,
∵DE是AB的垂直平分线,
∴AD=BD,AD⊥DE.
在Rt△ADE中,tan∠AED=.
∵tan∠AED=,
∴.
设AD=3k,则DE=4k.
∴.
∵AE=5,
∴5k=5.
∴k=1.
∴AD=3k=3.
∴AB=2AD=6.
∵AB=AC,
∴AC=6.
∴CE=AC﹣AE=6﹣5=1.
当DE与CA的延长线相交时,如图,
∵DE是AB的垂直平分线,
∴AD=BD,AD⊥DE.
在Rt△ADE中,tan∠AED=.
∵tan∠AED=,
∴.
设AD=3k,则DE=4k.
∴.
∵AE=5,
∴5k=5.
∴k=1.
∴AD=3k=3.
∴AB=2AD=6.
∵AB=AC,
∴AC=6.
∴CE=AC+AE=6+5=11.
综上,CE的长为1或11.
故答案为1或11.
13.解:过点A作AD⊥BC于D,过点B作BE⊥AC于E,如图,
在Rt△BEC中,
∵cosC=,
∴EC=BC cos60°=3.
∴BE=.
在Rt△BEA中,
AE=.
∴AC=AE+EC=3+1=4.
在Rt△ADC中,
∵cosC=,
∴CD=AC cos60°=2.
∴AD=.
BD=BC﹣CD=6﹣2=4.
在Rt△BAD中,tan∠B==.
故答案为:.
14.解:∵BD=AC,
∴=.
如图1所示:在Rt△ABD中,
∵AB=AC,sin45°=,
∵sinA===,
∴∠A=45°.
∴∠C==67.5°.
如图2所示:在Rt△ABD中,
∵AB=AC,sin45°=,
∵sin∠BAD===,
∴∠BAD=45°.
∴∠C==22.5°.
故答案为:67.5或22.5.
15.解:如图1,过点B作BM⊥CD,垂足为M,
∵CD⊥AC,
∴BM∥AC,
∴△DBM∽△DAC,
∴=,
又∵AB=3BD,AC=2,
∴==,
∴BM=,
在Rt△BMC中,由tan∠BCM=可得,BC=BM=,
如图2,过点B作BN⊥AC,交AC的延长线于N,
∵CD⊥AC,
∴BN∥CD,
∴△ADC∽△ABN,
∴=,
又∵AB=3BD,AC=2,
∴==,
∴CN=,
在Rt△BNC中,由tan∠CBN=tan∠BCD=可得,BC= CN=×=5,
故答案为:或5.
16.解:如图1,过点A作AM⊥BC,垂足为M,
∵AB=AC,AM⊥BC,
∴BM=CM=BC=12,
又∵tanC==tanB,
∴AM=BM tanB=12×=5,
∴AB=AC===13,
如图2,在Rt△APN中,PN=PC﹣CN=24﹣11﹣12=1,AN=5,
∴AP2=PN2+AN2=1+25=26,
在△APQ与△ACP中,
∵∠APQ=∠C,∠PAQ=∠CAP,
∴△APQ∽△ACP,
∴=,
∴AP2=AQ AC,
即26=AQ×13,
∴AQ=2,
故答案为:5,2.
17.解:如图,过端午A作AH⊥BC于H,过点C作CE⊥AD于E,连接AC.
在Rt△ABH中,tanB==,
∴可以假设AH=3k,BH=4k,则AB=5k=10,
∴k=2,
∴AH=6,BH=8,
∵BC=12,
∴CH=BC﹣BH=12﹣8=4,
∴AC===2,
∵∠B+∠D=90°,∠D+∠ECD=90°,
∴∠ECD=∠B,
在Rt△CED中,tan∠ECD==,
∵CD=5,
∴DE=3,CE=4,
∴AE===6,
∴AD=AE+DE=9.
故答案为:9.
18.解:作AF⊥BC于点F,
∵AB=AC,
∴AF平分∠BAC,BF=CF,
∴∠CAF=∠BAC,
即2∠CAF=∠BAC,
∵∠BAC=2∠EBC,
∴∠CAF=∠EBC,
∵∠CAF+∠ACF=90°,
∴∠EBC+∠ACF=90°,
∴∠BEC=90°,
∴∠AEB=90°,
∵tan∠BAC=,
∴设BE=3x,则AE=4x,
∴AB==5x,
∴AC=5x,
∴CE=x,
∵BC=,BE=3x,CE=x,
∴10=(3x)2+x2,
解得x1=1,x2=﹣1(舍去),
∴AC=5x=5,
∵∠AFC=90°,BF=BC=,
∴AF==,
∵点C为BD的中点,
∴FD=+=,
∵∠AFD=90°,
∴AD==3,
故答案为:3.
19.解:①如图1中,当△ABC是锐角三角形,CB=CA时,
在Rt△CDB中,BC==,
∴AD=AC﹣CD=﹣5,
∴tan∠ABD==.
②如图2中,当△ABC是钝角三角形,CB=CA时,
在Rt△CDB中,BC=AC==,
∴tan∠ABD==,
③如图3中,当△ABC是钝角三角形,AB=AC时,设AB=AC=x,
在Rt△ADB中,x2=32+(5﹣x)2,
∴x=,
∴tan∠ABD==,
综上所述,或或.
故答案为或或.
20.解:过D作DE⊥AB于E,过C作CF⊥DE于F,如图2所示:
则AE=CF,EF=AC=6cm,DE∥AC,
∴∠CDF+∠ACD=180°,
由题意得:∠A=∠BCD=90°,AB=AC=6cm,∠ABC=∠ACB=45°,∠CBD=30°,
∴∠ACD=45°+90°=135°,BC=AC=6(cm),CD=BC=2(cm),BD=2CD=4(cm),
∴∠DCF=45°,
∵CF⊥DE,
∴△CDF是等腰直角三角形,
∴AE=CF=DF=CD=2(cm),
∴BE=AB﹣AE=(6﹣2)cm,
∴DE===(6+2)cm,
∴sin75°=sin∠ABD===.
一、选择题
1.如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD,若AB=2BD,tan∠BCD=,则的值为( )
A.1
B.2
C.
D.
2.如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( )
A.
B.2
C.
D.
3.如图小张同学的尺规作图步骤,其具体做法如下:
①在射线AD上顺次截取AB=BC=a,②分别以B、C为圆心,以a为半径作圆弧,两弧交于点E,③连接AE、BE、CE,则下列说法错误的是( )
A.△BCE为等边三角形
B.△ACE的面积为
C.
D.∠AEC=3∠A
4.如图,在四边形ABCD中,∠ACB=∠CAD=90°,AC=CB,sin∠ACD=,则tan∠BDC的值是( )
A.
B.
C.
D.
5.如图,在Rt△ABC中,∠ACB=90°,D是边AB上一点,过D作DF⊥AB交边BC于点E,交AC的延长线于点F,联结AE,如果tan∠EAC=,S△CEF=1,那么S△ABC的值是( )
A.3
B.6
C.9
D.12
6.如图,在△ABC中,∠A=90°,sinB=,点D在边AB上,若AD=AC,则tan∠BCD的值为( )
A.
B.
C.
D.
二、填空题
7.一对直角三角形纸片ABC和BCD按如图所示方式摆放.其中∠BAC=∠BDC=90°,点A,D在BC的同侧,∠ABC=45°,tan∠DBC=.连接AD,若AB=5.则AD的长为
.
8.如图,在锐角△ABC中,cos∠BAC=,AB=AC,AE平分∠BAC交BC于点E,CD⊥AB于点D,AE,CD交于点F,连接DE.则=
.
9.如图,在边长为1的小正方形网格中,点A、B、C均在格点上,则tanB的值为
.
10.课堂上小刚进行如下实践操作:第一步,将一张矩形纸片利用图1的方法折出一个正方形,然后把纸片展平;第二步,如图2,把这个正方形折成两个全等的矩形,然后把纸片展平;第三步,如图3,折出内侧矩形AFBC的对角线AB,并把AB沿AQ对折到AD处,则tan∠BAQ=
.
11.如图,在△ABC中,∠ACB=90°,点D在边AC上,AD=4CD,若∠BAC=2∠CBD,则tanA=
.
12.在△ABC中,AB=AC,AB的垂直平分线DE与AC所在的直线相交于点E,垂足为D,连接BE.若AE=5,tan∠AED=,则CE=
.
13.在锐角△ABC中,∠ACB=60°,AB=2,BC=6,则∠B的正切值为
.
14.△ABC中,AB=AC,且高BD=AC,则∠C的大小为
度.
15.△ABC中,AC=2,点D为直线AB上一点,且AB=3BD,直线CD与直线BC所夹锐角的正切值为,并且CD⊥AC,则BC的长为
.
16.如图1,在△ABC中,AB=AC,BC=24,tanC=.点P为BC边上一点,则点P与点A的最短距离为
;如图2,连接AP,作∠APQ,使得∠APQ=∠B,PQ交AC于Q,则当BP=11时,求AQ.
三、解答题
17.新定义:有一组对角互余的凸四边形称为对余四边形,如图,已知在对余四边形ABCD中,AB=10,BC=12,CD=5,tanB=,求边AD的长.
18.如图,在△ABD中,点C为BD边中点,连接AC,点E在AC上,连接BE,若AB=AC,tan∠BAC=,∠BAC=2∠EBC,BC=,求AD的长.
19.等腰△ABC的腰AC边上的高BD=3,且CD=5,求tan∠ABD=
20.如图1,将一副三角板拼在一起(图2为示意图),则∠ABD=75°,已知AC=6cm,求sin75°的值.(结果保留根号)
参考答案
1.解:过点D作DM⊥BC,交CB的延长线于点M,
∵∠ACB=∠DMB=90°,∠ABC=∠DBM,
∴△ABC∽△DBM,
∴==,
∵AB=2BD,
∴===,
在Rt△CDM中,
由于tan∠MCD==,设DM=2k,则CM=3k,
又∵==,
∴BC=2k,AC=4k,
∴==2,
故选:B.
2.解:如图:
作OF⊥AB于F,
∵AB=AC,AD平分∠BAC.
∴∠ODB=90°.BD=CD=6.
∴根据勾股定理得:AD==8.
∵BE平分∠ABC.
∴OF=OD,BF=BD=6,AF=10﹣6=4.
设OD=OF=x,则AO=8﹣x,在Rt△AOF中,根据勾股定理得:
(8﹣x)2=x2+42.
∴x=3.
∴OD=3.
在Rt△OBD中,tan∠OBD===.
故选:A.
3.解:由题意得AB=BC=BE=CE=a,
∴△BCE为等边三角形,故A选项正确.
∴△BCE的面积为,故B选项错误.
∵BE=BA,∠EBC=60°,
∴∠A=∠BEA=30°,
∴sinA=sin30°=,故C选项正确.
∴∠AEC=∠BEA+∠BEC=30°+60°=90°,
∴∠AEC=3∠A,故D选项正确.
故选:B.
4.解:如图,过点D作DE⊥BC交BC的延长线于E,过点C作CH⊥BD于H.
∵∠ACB=∠CAD=90°,DE⊥EC,
∴∠ACE=∠E=90°,
∴四边形ACED是矩形,
∴AD=CE,AC=DE,
∵sin∠ACD==,
∴可以假设AD=3k,CD=5k,则AC=BC=DE=4k,
∴BE=BC+CE=7k,
∴BD===k,
∵S△CBD= BC DE= BD CH,
∴CH=k,
∴DH===k,
∴tan∠BDC==.
方法二:过点B作BH垂于DC交DC的延长线于点H,
设AD=3k,CD=5k,则AC=BC=4k,
∵∠H=∠CAD=∠ACB=90°,
∴∠ACD+∠BCH=90°,∠CBH+∠BCH=90°,
∴∠ACD=∠CBH,
∴△CBH∽△DCA,
∴==,
∴==,
∴BH=k,CH=k,
∴DH=CH+CD=k+5k=k,
tan∠BDC==.
故选:C.
5.解:∵∠ACB=90°,
∴∠BAC+∠B=90°,
又∵DF⊥AB,
∴∠ADF=90°,
∴∠BAC+∠F=90°,
∴∠B=∠F,
又∵∠ECF=∠ACB=90°,
∴△ECF∽△ACB,
∴==tan∠EAC=,
∴=,
又∵S△ECF=1,
∴S△ABC=9,
故选:C.
6.解:如图,作DH⊥BC于H.
∵∠A=90°,sinB==,
∴可以假设AC=3k,BC=5k,则AB=4k,
∵AC=AD=3k,
∴BD=k,
∵∠B=∠B,∠DHB=∠A=90°,
∴△BHD∽△BAC,
∴==,
∴==,
∴DH=k,BH=k,
∵CH=BC﹣BH=5k﹣k=k,
∴tan∠BCD===,
故选:C.
7.解:如图,分别过点A、D作AF⊥BC、DE⊥BC,交BC于点F、E,过点D作DM⊥AF,于点M,
在Rt△ABC中,
∵AB=5,∠ABC=45°,
∴AC=AB=5,BC=10,
∴AF=BF=5,
在Rt△BCD中,
∵tan∠DBC=,
∴BD=6,
在Rt△BDE中,
∵tan∠DBE=,
∴DE=,BE=,
∵∠DEF=∠DMF=∠EFM=90°,
∴四边形DEFM是矩形,
∴DM=EF=BF﹣BE=,MF=DE=,
∴AM=AF﹣MF=,
在Rt△ADM中,由勾股定理,得:AD==,
故答案为:.
8.解:如图,在AE上取一点M,使得AM=MC.设EC=m.
∵cos∠BAC=,
∴∠BAC=45°,
∵AB=AC,AE平分∠BAC,
∴AE⊥BC,∠EAC=∠BAC=22.5°,
∵MA=MC,
∴∠MAC=∠MCA=22.5°,
∴∠CME=∠MAC+∠MCA=45°,
∴EC=EM=m,AM=CM=m,AE=m+m,
∵∠ADC=∠AEC=90°,
∴A,D,E,C四点共圆,
∴∠ECF=∠DAE=22.5°,
∵∠DAE=∠EAC,
∴=,
∴DE=ED,
∴===tan22.5°==﹣1.
故答案为:﹣1
9.解:如图,取格点E,连接AE,EC,则B,A,E共线,∠E=90°.
∵EC==,BE==2,
∴tanB==.
故答案为:.
10.解:过点Q作QH⊥AD,垂足为H,
由折叠可知,∠BAQ=∠QAH,AB=AD,
又∵MQ∥NH,
∴∠QAH=∠BQA,
∴∠BAQ=∠BQA,
∴AB=BQ,
∴四边形ADQB是菱形,
∴AB=QD,
又∵BC=QH,
∴△ABC≌△DQH
(HL),
∴AC=DH,
设AC=a=DH,则BC=2a=QH,
∴AB==a,
∴AH=a+a=(+1)a,
在Rt△AQH中,tan∠QAH===.
即tan∠BAQ=tan∠QAH=.
11.解:延长AC至E,使CE=CD,连接BE,
∵∠ACB=90°,
∴BC⊥AC,
∵CE=CD,
∴BC是DE的垂直平分线,
∴BD=BE,
∴∠E=∠BDE,
设∠CBD=α,则∠BAC=2α,
∴∠E=∠BDE=90°﹣α,
∴∠ABE=180°﹣∠E﹣BAC=180°﹣(90°﹣α)﹣2α=90°﹣α,
∴∠E=∠ABE,
∴AB=AE,
设CD=x,则AD=4x,
∴AE=AB=6x,AC=5x,
在Rt△ABC中,BC===x,
∴tanA==.
故答案为:.
12.解:分两种情形:
当DE与AC边相交时,如图,
∵DE是AB的垂直平分线,
∴AD=BD,AD⊥DE.
在Rt△ADE中,tan∠AED=.
∵tan∠AED=,
∴.
设AD=3k,则DE=4k.
∴.
∵AE=5,
∴5k=5.
∴k=1.
∴AD=3k=3.
∴AB=2AD=6.
∵AB=AC,
∴AC=6.
∴CE=AC﹣AE=6﹣5=1.
当DE与CA的延长线相交时,如图,
∵DE是AB的垂直平分线,
∴AD=BD,AD⊥DE.
在Rt△ADE中,tan∠AED=.
∵tan∠AED=,
∴.
设AD=3k,则DE=4k.
∴.
∵AE=5,
∴5k=5.
∴k=1.
∴AD=3k=3.
∴AB=2AD=6.
∵AB=AC,
∴AC=6.
∴CE=AC+AE=6+5=11.
综上,CE的长为1或11.
故答案为1或11.
13.解:过点A作AD⊥BC于D,过点B作BE⊥AC于E,如图,
在Rt△BEC中,
∵cosC=,
∴EC=BC cos60°=3.
∴BE=.
在Rt△BEA中,
AE=.
∴AC=AE+EC=3+1=4.
在Rt△ADC中,
∵cosC=,
∴CD=AC cos60°=2.
∴AD=.
BD=BC﹣CD=6﹣2=4.
在Rt△BAD中,tan∠B==.
故答案为:.
14.解:∵BD=AC,
∴=.
如图1所示:在Rt△ABD中,
∵AB=AC,sin45°=,
∵sinA===,
∴∠A=45°.
∴∠C==67.5°.
如图2所示:在Rt△ABD中,
∵AB=AC,sin45°=,
∵sin∠BAD===,
∴∠BAD=45°.
∴∠C==22.5°.
故答案为:67.5或22.5.
15.解:如图1,过点B作BM⊥CD,垂足为M,
∵CD⊥AC,
∴BM∥AC,
∴△DBM∽△DAC,
∴=,
又∵AB=3BD,AC=2,
∴==,
∴BM=,
在Rt△BMC中,由tan∠BCM=可得,BC=BM=,
如图2,过点B作BN⊥AC,交AC的延长线于N,
∵CD⊥AC,
∴BN∥CD,
∴△ADC∽△ABN,
∴=,
又∵AB=3BD,AC=2,
∴==,
∴CN=,
在Rt△BNC中,由tan∠CBN=tan∠BCD=可得,BC= CN=×=5,
故答案为:或5.
16.解:如图1,过点A作AM⊥BC,垂足为M,
∵AB=AC,AM⊥BC,
∴BM=CM=BC=12,
又∵tanC==tanB,
∴AM=BM tanB=12×=5,
∴AB=AC===13,
如图2,在Rt△APN中,PN=PC﹣CN=24﹣11﹣12=1,AN=5,
∴AP2=PN2+AN2=1+25=26,
在△APQ与△ACP中,
∵∠APQ=∠C,∠PAQ=∠CAP,
∴△APQ∽△ACP,
∴=,
∴AP2=AQ AC,
即26=AQ×13,
∴AQ=2,
故答案为:5,2.
17.解:如图,过端午A作AH⊥BC于H,过点C作CE⊥AD于E,连接AC.
在Rt△ABH中,tanB==,
∴可以假设AH=3k,BH=4k,则AB=5k=10,
∴k=2,
∴AH=6,BH=8,
∵BC=12,
∴CH=BC﹣BH=12﹣8=4,
∴AC===2,
∵∠B+∠D=90°,∠D+∠ECD=90°,
∴∠ECD=∠B,
在Rt△CED中,tan∠ECD==,
∵CD=5,
∴DE=3,CE=4,
∴AE===6,
∴AD=AE+DE=9.
故答案为:9.
18.解:作AF⊥BC于点F,
∵AB=AC,
∴AF平分∠BAC,BF=CF,
∴∠CAF=∠BAC,
即2∠CAF=∠BAC,
∵∠BAC=2∠EBC,
∴∠CAF=∠EBC,
∵∠CAF+∠ACF=90°,
∴∠EBC+∠ACF=90°,
∴∠BEC=90°,
∴∠AEB=90°,
∵tan∠BAC=,
∴设BE=3x,则AE=4x,
∴AB==5x,
∴AC=5x,
∴CE=x,
∵BC=,BE=3x,CE=x,
∴10=(3x)2+x2,
解得x1=1,x2=﹣1(舍去),
∴AC=5x=5,
∵∠AFC=90°,BF=BC=,
∴AF==,
∵点C为BD的中点,
∴FD=+=,
∵∠AFD=90°,
∴AD==3,
故答案为:3.
19.解:①如图1中,当△ABC是锐角三角形,CB=CA时,
在Rt△CDB中,BC==,
∴AD=AC﹣CD=﹣5,
∴tan∠ABD==.
②如图2中,当△ABC是钝角三角形,CB=CA时,
在Rt△CDB中,BC=AC==,
∴tan∠ABD==,
③如图3中,当△ABC是钝角三角形,AB=AC时,设AB=AC=x,
在Rt△ADB中,x2=32+(5﹣x)2,
∴x=,
∴tan∠ABD==,
综上所述,或或.
故答案为或或.
20.解:过D作DE⊥AB于E,过C作CF⊥DE于F,如图2所示:
则AE=CF,EF=AC=6cm,DE∥AC,
∴∠CDF+∠ACD=180°,
由题意得:∠A=∠BCD=90°,AB=AC=6cm,∠ABC=∠ACB=45°,∠CBD=30°,
∴∠ACD=45°+90°=135°,BC=AC=6(cm),CD=BC=2(cm),BD=2CD=4(cm),
∴∠DCF=45°,
∵CF⊥DE,
∴△CDF是等腰直角三角形,
∴AE=CF=DF=CD=2(cm),
∴BE=AB﹣AE=(6﹣2)cm,
∴DE===(6+2)cm,
∴sin75°=sin∠ABD===.
