2021-2022学年鲁教版(五四制)九年级数学上册2.4解直角三角形同步能力达标测评(word解析版)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)九年级数学上册2.4解直角三角形同步能力达标测评(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 571.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 00:00:00 | ||
图片预览



文档简介
2021-2022学年鲁教版九年级数学上册《2.4解直角三角形》同步能力达标测评(附答案)
一.选择题(共15小题,满分45分)
1.在Rt△ABC中,∠C=90°,下列关系式中错误的是( )
A.BC=AB sinA
B.BC=AC tanA
C.AC=BC tanB
D.AC=AB cosB
2.如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD=( )
A.
B.3
C.
D.2
3.如图,在正方形方格纸中,每个小方格边长为1,A,B,C,D都在格点处,AB与CD相交于点O,则sin∠BOD的值等于( )
A.
B.
C.
D.
4.如图,在△ABC中,∠BAC=120°,AC=6,AB=4,则BC的长是( )
A.6
B.2
C.2
D.9
5.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD的值为( )
A.
B.
C.
D.2
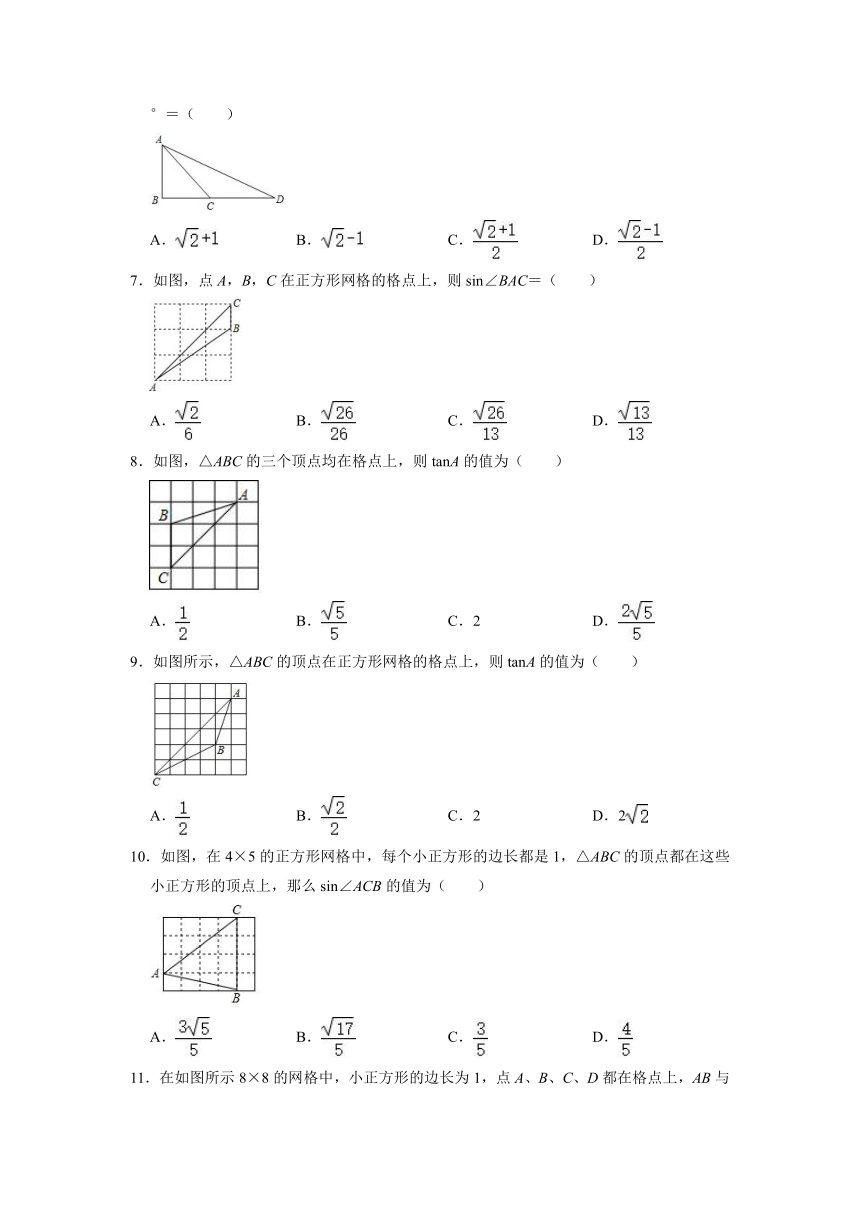
6.如图Rt△ABC中,∠B=90°,∠ACB=45°,延长BC到D,使CD=AC,则tan22.5°=( )
A.
B.
C.
D.
7.如图,点A,B,C在正方形网格的格点上,则sin∠BAC=( )
A.
B.
C.
D.
8.如图,△ABC的三个顶点均在格点上,则tanA的值为( )
A.
B.
C.2
D.
9.如图所示,△ABC的顶点在正方形网格的格点上,则tanA的值为( )
A.
B.
C.2
D.2
10.如图,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为( )
A.
B.
C.
D.
11.在如图所示8×8的网格中,小正方形的边长为1,点A、B、C、D都在格点上,AB与CD相交于点E,则∠AED的正切值是( )
A.2
B.
C.
D.
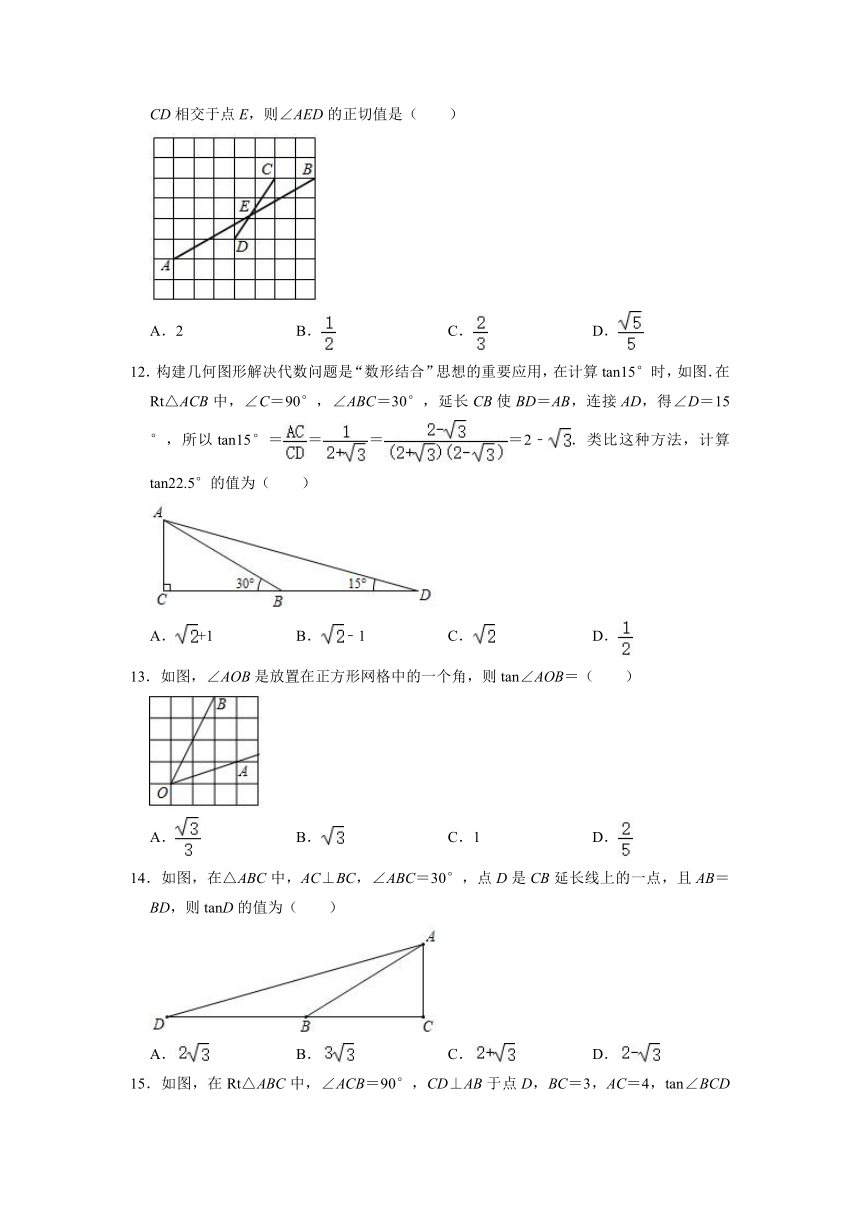
12.构建几何图形解决代数问题是“数形结合”思想的重要应用,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°====2﹣.类比这种方法,计算tan22.5°的值为( )
A.+1
B.﹣1
C.
D.
13.如图,∠AOB是放置在正方形网格中的一个角,则tan∠AOB=( )
A.
B.
C.1
D.
14.如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且AB=BD,则tanD的值为( )
A.
B.
C.
D.
15.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,BC=3,AC=4,tan∠BCD的值为( )
A.
B.
C.
D.
二.填空题(共4小题,满分12分)
16.如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中cos∠ABC=
.
17.如图,在四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD.若,则tanD=
.
18.如图所示,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,若sin∠ACB=,则cos∠ADC=
.
19.已知△ABC,O为AC中点,点P在AC上,若OP=,tan∠A=,∠B=120°,BC=2,则AP=
.
三.解答题(共11小题,满分63分)
20.通过学习锐角三角比,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此,两条边长的比值与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can),如图(1)在△ABC中,AB=AC,底角B的邻对记作canB,这时canB=,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义,解下列问题:
(1)can30°=
;
(2)如图(2),已知在△ABC中,AB=AC,canB=,S△ABC=24,求△ABC的周长.
21.阅读下列材料:
如图1,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,可以得到:
S△ABC=absinC=acsinB=bcsinA
证明:过点A作AD⊥BC,垂足为D.
在Rt△ABD中,sinB=
∴AD=c sinB
∴S△ABC=a AD=acsinB
同理:S△ABC=absinC
S△ABC=bcsinA
∴S△ABC=absinC=acsinB=bcsinA
(1)通过上述材料证明:
==
(2)运用(1)中的结论解决问题:
如图2,在△ABC中,∠B=15°,∠C=60°,AB=20,求AC的长度.
(3)如图3,为了开发公路旁的城市荒地,测量人员选择A、B、C三个测量点,在B点测得A在北偏东75°方向上,沿笔直公路向正东方向行驶18km到达C点,测得A在北偏西45°方向上,根据以上信息,求A、B、C三点围成的三角形的面积.
(本题参考数值:sin15°≈0.3,sin120°≈0.9,≈1.4,结果取整数)
22.如图①,在Rt△ABC中,以下是小亮探究与之间关系的方法:
∵sinA=,sinB=
∴c=,c=
∴=
根据你掌握的三角函数知识.在图②的锐角△ABC中,探究、、之间的关系,并写出探究过程.
23.如图所示,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知∠α=36°,求长方形卡片的周长.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
24.已知:如图1,在锐角△ABC中,AB=c,BC=a,AC=b,AD⊥BC于D.
在Rt△ABD中,sin∠B=,则AD=csin∠B;
在Rt△ACD中,sin∠C=
,则AD=
;
所以,csin∠B=bsin∠C,即,,
进一步即得正弦定理:(此定理适合任意锐角三角形).
参照利用正弦定理解答下题:
如图2,在△ABC中,∠B=75°,∠C=45°,BC=2,求AB的长.
25.阅读下面材料:
小天在学习锐角三角函数中遇到这样一个问题:在Rt△ABC中,∠C=90°,∠B=22.5°,则tan22.5°=
小天根据学习几何的经验,先画出了几何图形(如图1),他发现22.5°不是特殊角,但它是特殊角45°的一半,若构造有特殊角的直角三角形,则可能解决这个问题.于是小天尝试着在CB边上截取CD=CA,连接AD(如图2),通过构造有特殊角(45°)的直角三角形,经过推理和计算使问题得到解决.
请回答:tan22.5°=
.
参考小天思考问题的方法,解决问题:
如图3,在等腰△ABC
中,AB=AC,∠A=30°,请借助△ABC,构造出15°的角,并求出该角的正切值.
26.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC=12,试求CD的长.
27.已知:在Rt△ABC,∠C=90°,D是BC边的中点,DE⊥AB于E,tanB=,AE=7,求DE.
28.通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA==.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:
(1)sad60°=
;
(2)对于0°<A<180°,∠A的正对值sadA的取值范围是
;
(3)如图,已知cosA=,其中∠A为锐角,试求sadA的值.
29.如图,在△ABC中,AB=AC=5,BC=8,D是边AB上一点,且tan∠BCD=.
(1)试求sinB的值;
(2)试求△BCD的面积.
参考答案
一.选择题(共15小题,满分45分)
1.解:如图所示:
∵sinA=,∴BC=sinA×AB,故选项A正确;
∵tanA=,∴BC=tanA×AC,故选项B正确;
∵tanB=,∴AC=tanB×BC,故选项C正确;
∵cosB=,∴BC=cosB×AB≠AC,故选项D错误.
故选:D.
2.解:设小正方形的边长为1,
由图形可知,,
∴△ADC是等腰直角三角形,
∴AD⊥DC.
∵AC∥BD,
∴,
∴PC=2DP,
∴AD=DC=3DP,
∴.
故选:B.
3.解:连接AE、EF,如图所示,
则AE∥CD,
∴∠FAE=∠BOD,
∵每个小正方形的边长为1,
则AE==,AF==2,EF==3,
∵()2+(3)2=(2)2,
∴△FAE是直角三角形,∠FEA=90°,
∴sin∠FAE===,
∴sin∠BOD=,
故选:B.
4.解:过点C作CD⊥AB,交BA的延长线于点D,
∵∠BAC=120°,
∴∠DAC=180°﹣120°=60°,
∴∠ACD=30°,
∴AD=AC=3,
∴BD=AB+AD=7,
由勾股定理得,CD==3,
在Rt△BCD中,BC==2,
故选:B.
5.解:延长AD、BC,两线交于O,
∵在Rt△ABO中,∠B=90°,tanA==,AB=3,
∴OB=4,
∵BC=2,
∴OC=OB﹣BC=4﹣2=2,
在Rt△ABO中,∠B=90°,AB=3,OB=4,由勾股定理得:AO=5,
∵∠ADC=90°,
∴∠ODC=90°=∠B,
∵∠O=∠O,
∴△ODC∽△OBA,
∴=,
∴=,
解得:DC=,
故选:C.
6.解:设AB=x,
∵在Rt△ABC中,∠B=90°,∠ACB=45°,
∴∠BAC=∠ACB=45°,
∴AB=BC=x,
由勾股定理得:AC==x,
∵AC=CD,
∴AC=CD=x,
∴BD=BC+CD=(+1)x,
∴tan22.5°===﹣1,
故选:B.
7.解:如图,过点B作BD⊥AC于D,
由勾股定理得,AB==,AC==3,
∵S△ABC=AC BD=×3 BD=×1×3,
∴BD=,
∴sin∠BAC===.
故选:B.
8.解:如图所示:连接BD,
BD==,
AD==2,
AB==,
∵BD2+AD2=2+8=10=AB2,
∴△ADB为直角三角形,
∴∠ADB=90°,
则tanA===.
故选:A.
9.解:如图,连接BD,由网格的特点可得,BD⊥AC,
AD==2,BD==,
∴tanA===,
故选:A.
10.解:如图,过点A作AH⊥BC于H.
在Rt△ACH中,∵AH=4,CH=3,
∴AC===5,
∴sin∠ACH==,
故选:D.
11.解:如图,取格点K,连接AK,BK.
观察图形可知AK⊥BK,BK=2AK,BK∥CD,
∴∠AED=∠ABK,
∴tan∠AED=tan∠ABK==,
故选:B.
12.解:在Rt△ACB中,∠C=90°,∠ABC=45°,延长CB使BD=AB,连接AD,得∠D=22.5°,
设AC=BC=1,则AB=BD=,
∴tan22.5°===﹣1,
故选:B.
13.解:如图,连接AB.
观察图象可知△AOB是等腰直角三角形,
∴∠AOB=45°,AB=OA,
∴tan∠AOB==1,
故选:C.
14.解:设AC=m,
在Rt△ABC中,∵∠C=90°,∠ABC=30°,
∴AB=2AC=2m,BC=AC=m,
∴BD=AB=2m,DC=2m+m,
∴tan∠ADC===2﹣.
故选:D.
15.解:∵∠ACB=90°,
∴∠A+∠B=90°,
∵CD⊥AB,
∴∠BCD+∠B=90°,
∴∠BCD=∠A,
∴tan∠BCD=tan∠A==,
故选:A.
二.填空题(共4小题,满分12分)
16.解:由图可知,AC2=22+42=20,BC2=12+22=5,AB2=32+42=25,
∴△ABC是直角三角形,且∠ACB=90°,
∴cos∠ABC=,
故答案为:.
17.解:∵∠B=90°,sin∠ACB=,
∴=,
∵AB=2,
∴AC=6,
∵AC⊥CD,
∴∠ACD=90°,
∴tan∠ADC===.
故答案为:.
18.解:∵∠B=90°,sin∠ACB=,
∴=,
∵AB=2,
∴AC=6,
∵AC⊥CD,
∴∠ACD=90°,
∴AD===10,
∴cos∠ADC==.
故答案为:.
19.解:作CD⊥AB的延长线于D,
∵∠ABC=120°,
∴∠CBD=60°,
∵BC=2,
∴DC=BC sin60°=2 =3,
∵tan∠A=,
∴AD=6,
∴AC==3,
∴AO=,
∵OP=,
∴AP=2或.
故答案为2或.
三.解答题(共10小题,满分63分)
20.解:
(1)过点A作AD⊥BC于点D,
∵∠B=30°,
∴cos∠B==,
∴BD=AB,
∵△ABC是等腰三角形,
∴BC=2BD=AB,
故can30°==;
(2)过点A作AE⊥BC于点E,
∵canB=,则可设BC=8x,AB=5x,
∴AE==3x,
∵S△ABC=24,
∴BC×AE=12x2=24,
解得:x=,
故AB=AC=5,BC=8,
从而可得△ABC的周长为18.
21.解:(1)∵absinC=acsinB,
∴bsinC=csinB,
∴=,
:同理得:=,
∴==;
(2)由题意得:∠B=15°,∠C=60°,AB=20,
∴,即,
∴,
∴AC≈40×0.3=12;
(3)由题意得:∠ABC=90°﹣75°=15°,∠ACB=90°﹣45°=45°,
∠A=180°﹣15°﹣45°=120°,
由==得:=,
∴AC≈6,
∴S△ABC=AC×BC×sin∠ACB≈×6×18×0.7≈38.
22.解:==,理由为:
过A作AD⊥BC,BE⊥AC,
在Rt△ABD中,sinB=,即AD=csinB,
在Rt△ADC中,sinC=,即AD=bsinC,
∴csinB=bsinC,即=,
同理可得=,
则==.
23.解:作BE⊥l于点E,DF⊥l于点F.
根据题意,得BE=24mm,DF=48mm.
在Rt△ABE中,sin
,
∴mm
在Rt△ADF中,cos
,
∴mm.
∴矩形ABCD的周长=2(40+60)=200mm.
24.解:在Rt△ACD中,sin∠C=,则AD=bsin∠C,
故答案为:,bsin∠C;
如图2,在△ABC中,∠B=75°,∠C=45°,BC=2,
则∠A=60°,
∵,
∴,
即,
解得,AB=,
即AB的长是.
25.解:如图2,设CD=CA=a,则AD=a,
∵∠B=22.5°,∠ADC=45°,
∴∠DAB=22.5°,
∴∠DAB=∠B,
∴DB=DA=a,
∴BC=BD+CD=(+1)a,
在Rt△ABC中,tanB===﹣1,
即tan22.5°=﹣1;
故答案为﹣1;﹣1;
如图3,延长BA到D,使AD=AB,则AB=AD=AC,
∴∠D=∠ACD,
∵∠CAB=∠D+∠ACD=30°,
∴∠D=15°,
作CH⊥AB于H,设CH=x,则AC=2x,AH=x,
∴AD=AC=2x,
∴DH=AD+AH=(2+)x,
在Rt△DCH中,tanD===2﹣,
即tan15°=2﹣.
26.解:过点B作BM⊥FD于点M,
在△ACB中,∠ACB=90°,∠A=45°,AC=12,
∴BC=AC=12
∵AB∥CF,
∴BM=BC×sin45°=12×=12
CM=BM=12,
在△EFD中,∠F=90°,∠E=30°,
∴∠EDF=60°,
∴MD=BM÷tan60°=4,
∴CD=CM﹣MD=12﹣4.
27.解:∵DE⊥AB于E,
∴tanB==,
设DE=x,
∴BE=2x,
∴BD==,
∴cosB==,
∵∠C=90°,∴cosB===,
∵D是BC边的中点,∴BC=2BD=2,
∴AB=,
∵AE=7,
∴AB=AE+BE,
5x=7+2x,
x=.
故DE=.
28.解:(1)根据正对定义,
当顶角为60°时,等腰三角形底角为60°,
则三角形为等边三角形,
则sad60°==1.
故答案为:1.
(2)当∠A接近0°时,sadA接近0,
当∠A接近180°时,等腰三角形的底接近于腰的二倍,故sadA接近2.
于是sadA的取值范围是0<sadA<2.
故答案为0<sadA<2.
(3)如图,过B作BD⊥AC于D.
在Rt△ABD中,cosA==.
设AD=4k,AB=5k,则BD=3k,
∴DC=5k﹣4k=k.
在Rt△BDC中,BC==k,
∴sadA==.
29.解:(1)作AH⊥BC,垂足为H,
∵AB=AC=5,∴BH=BC=4,
在△ABH中,AH==3,
∴.
(2)作DE⊥BC,垂足为E,
在△BDE中,sinB=,令DE=3k,
BD=5k,则BE==4k,
又在△CDE中,tan∠BCD=,
则CE==6k,
于是BC=BE+EC,即4k+6k=8,
解得,
∴.
一.选择题(共15小题,满分45分)
1.在Rt△ABC中,∠C=90°,下列关系式中错误的是( )
A.BC=AB sinA
B.BC=AC tanA
C.AC=BC tanB
D.AC=AB cosB
2.如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD=( )
A.
B.3
C.
D.2
3.如图,在正方形方格纸中,每个小方格边长为1,A,B,C,D都在格点处,AB与CD相交于点O,则sin∠BOD的值等于( )
A.
B.
C.
D.
4.如图,在△ABC中,∠BAC=120°,AC=6,AB=4,则BC的长是( )
A.6
B.2
C.2
D.9
5.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD的值为( )
A.
B.
C.
D.2
6.如图Rt△ABC中,∠B=90°,∠ACB=45°,延长BC到D,使CD=AC,则tan22.5°=( )
A.
B.
C.
D.
7.如图,点A,B,C在正方形网格的格点上,则sin∠BAC=( )
A.
B.
C.
D.
8.如图,△ABC的三个顶点均在格点上,则tanA的值为( )
A.
B.
C.2
D.
9.如图所示,△ABC的顶点在正方形网格的格点上,则tanA的值为( )
A.
B.
C.2
D.2
10.如图,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为( )
A.
B.
C.
D.
11.在如图所示8×8的网格中,小正方形的边长为1,点A、B、C、D都在格点上,AB与CD相交于点E,则∠AED的正切值是( )
A.2
B.
C.
D.
12.构建几何图形解决代数问题是“数形结合”思想的重要应用,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°====2﹣.类比这种方法,计算tan22.5°的值为( )
A.+1
B.﹣1
C.
D.
13.如图,∠AOB是放置在正方形网格中的一个角,则tan∠AOB=( )
A.
B.
C.1
D.
14.如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且AB=BD,则tanD的值为( )
A.
B.
C.
D.
15.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,BC=3,AC=4,tan∠BCD的值为( )
A.
B.
C.
D.
二.填空题(共4小题,满分12分)
16.如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中cos∠ABC=
.
17.如图,在四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD.若,则tanD=
.
18.如图所示,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,若sin∠ACB=,则cos∠ADC=
.
19.已知△ABC,O为AC中点,点P在AC上,若OP=,tan∠A=,∠B=120°,BC=2,则AP=
.
三.解答题(共11小题,满分63分)
20.通过学习锐角三角比,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此,两条边长的比值与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can),如图(1)在△ABC中,AB=AC,底角B的邻对记作canB,这时canB=,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义,解下列问题:
(1)can30°=
;
(2)如图(2),已知在△ABC中,AB=AC,canB=,S△ABC=24,求△ABC的周长.
21.阅读下列材料:
如图1,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,可以得到:
S△ABC=absinC=acsinB=bcsinA
证明:过点A作AD⊥BC,垂足为D.
在Rt△ABD中,sinB=
∴AD=c sinB
∴S△ABC=a AD=acsinB
同理:S△ABC=absinC
S△ABC=bcsinA
∴S△ABC=absinC=acsinB=bcsinA
(1)通过上述材料证明:
==
(2)运用(1)中的结论解决问题:
如图2,在△ABC中,∠B=15°,∠C=60°,AB=20,求AC的长度.
(3)如图3,为了开发公路旁的城市荒地,测量人员选择A、B、C三个测量点,在B点测得A在北偏东75°方向上,沿笔直公路向正东方向行驶18km到达C点,测得A在北偏西45°方向上,根据以上信息,求A、B、C三点围成的三角形的面积.
(本题参考数值:sin15°≈0.3,sin120°≈0.9,≈1.4,结果取整数)
22.如图①,在Rt△ABC中,以下是小亮探究与之间关系的方法:
∵sinA=,sinB=
∴c=,c=
∴=
根据你掌握的三角函数知识.在图②的锐角△ABC中,探究、、之间的关系,并写出探究过程.
23.如图所示,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知∠α=36°,求长方形卡片的周长.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
24.已知:如图1,在锐角△ABC中,AB=c,BC=a,AC=b,AD⊥BC于D.
在Rt△ABD中,sin∠B=,则AD=csin∠B;
在Rt△ACD中,sin∠C=
,则AD=
;
所以,csin∠B=bsin∠C,即,,
进一步即得正弦定理:(此定理适合任意锐角三角形).
参照利用正弦定理解答下题:
如图2,在△ABC中,∠B=75°,∠C=45°,BC=2,求AB的长.
25.阅读下面材料:
小天在学习锐角三角函数中遇到这样一个问题:在Rt△ABC中,∠C=90°,∠B=22.5°,则tan22.5°=
小天根据学习几何的经验,先画出了几何图形(如图1),他发现22.5°不是特殊角,但它是特殊角45°的一半,若构造有特殊角的直角三角形,则可能解决这个问题.于是小天尝试着在CB边上截取CD=CA,连接AD(如图2),通过构造有特殊角(45°)的直角三角形,经过推理和计算使问题得到解决.
请回答:tan22.5°=
.
参考小天思考问题的方法,解决问题:
如图3,在等腰△ABC
中,AB=AC,∠A=30°,请借助△ABC,构造出15°的角,并求出该角的正切值.
26.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC=12,试求CD的长.
27.已知:在Rt△ABC,∠C=90°,D是BC边的中点,DE⊥AB于E,tanB=,AE=7,求DE.
28.通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA==.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:
(1)sad60°=
;
(2)对于0°<A<180°,∠A的正对值sadA的取值范围是
;
(3)如图,已知cosA=,其中∠A为锐角,试求sadA的值.
29.如图,在△ABC中,AB=AC=5,BC=8,D是边AB上一点,且tan∠BCD=.
(1)试求sinB的值;
(2)试求△BCD的面积.
参考答案
一.选择题(共15小题,满分45分)
1.解:如图所示:
∵sinA=,∴BC=sinA×AB,故选项A正确;
∵tanA=,∴BC=tanA×AC,故选项B正确;
∵tanB=,∴AC=tanB×BC,故选项C正确;
∵cosB=,∴BC=cosB×AB≠AC,故选项D错误.
故选:D.
2.解:设小正方形的边长为1,
由图形可知,,
∴△ADC是等腰直角三角形,
∴AD⊥DC.
∵AC∥BD,
∴,
∴PC=2DP,
∴AD=DC=3DP,
∴.
故选:B.
3.解:连接AE、EF,如图所示,
则AE∥CD,
∴∠FAE=∠BOD,
∵每个小正方形的边长为1,
则AE==,AF==2,EF==3,
∵()2+(3)2=(2)2,
∴△FAE是直角三角形,∠FEA=90°,
∴sin∠FAE===,
∴sin∠BOD=,
故选:B.
4.解:过点C作CD⊥AB,交BA的延长线于点D,
∵∠BAC=120°,
∴∠DAC=180°﹣120°=60°,
∴∠ACD=30°,
∴AD=AC=3,
∴BD=AB+AD=7,
由勾股定理得,CD==3,
在Rt△BCD中,BC==2,
故选:B.
5.解:延长AD、BC,两线交于O,
∵在Rt△ABO中,∠B=90°,tanA==,AB=3,
∴OB=4,
∵BC=2,
∴OC=OB﹣BC=4﹣2=2,
在Rt△ABO中,∠B=90°,AB=3,OB=4,由勾股定理得:AO=5,
∵∠ADC=90°,
∴∠ODC=90°=∠B,
∵∠O=∠O,
∴△ODC∽△OBA,
∴=,
∴=,
解得:DC=,
故选:C.
6.解:设AB=x,
∵在Rt△ABC中,∠B=90°,∠ACB=45°,
∴∠BAC=∠ACB=45°,
∴AB=BC=x,
由勾股定理得:AC==x,
∵AC=CD,
∴AC=CD=x,
∴BD=BC+CD=(+1)x,
∴tan22.5°===﹣1,
故选:B.
7.解:如图,过点B作BD⊥AC于D,
由勾股定理得,AB==,AC==3,
∵S△ABC=AC BD=×3 BD=×1×3,
∴BD=,
∴sin∠BAC===.
故选:B.
8.解:如图所示:连接BD,
BD==,
AD==2,
AB==,
∵BD2+AD2=2+8=10=AB2,
∴△ADB为直角三角形,
∴∠ADB=90°,
则tanA===.
故选:A.
9.解:如图,连接BD,由网格的特点可得,BD⊥AC,
AD==2,BD==,
∴tanA===,
故选:A.
10.解:如图,过点A作AH⊥BC于H.
在Rt△ACH中,∵AH=4,CH=3,
∴AC===5,
∴sin∠ACH==,
故选:D.
11.解:如图,取格点K,连接AK,BK.
观察图形可知AK⊥BK,BK=2AK,BK∥CD,
∴∠AED=∠ABK,
∴tan∠AED=tan∠ABK==,
故选:B.
12.解:在Rt△ACB中,∠C=90°,∠ABC=45°,延长CB使BD=AB,连接AD,得∠D=22.5°,
设AC=BC=1,则AB=BD=,
∴tan22.5°===﹣1,
故选:B.
13.解:如图,连接AB.
观察图象可知△AOB是等腰直角三角形,
∴∠AOB=45°,AB=OA,
∴tan∠AOB==1,
故选:C.
14.解:设AC=m,
在Rt△ABC中,∵∠C=90°,∠ABC=30°,
∴AB=2AC=2m,BC=AC=m,
∴BD=AB=2m,DC=2m+m,
∴tan∠ADC===2﹣.
故选:D.
15.解:∵∠ACB=90°,
∴∠A+∠B=90°,
∵CD⊥AB,
∴∠BCD+∠B=90°,
∴∠BCD=∠A,
∴tan∠BCD=tan∠A==,
故选:A.
二.填空题(共4小题,满分12分)
16.解:由图可知,AC2=22+42=20,BC2=12+22=5,AB2=32+42=25,
∴△ABC是直角三角形,且∠ACB=90°,
∴cos∠ABC=,
故答案为:.
17.解:∵∠B=90°,sin∠ACB=,
∴=,
∵AB=2,
∴AC=6,
∵AC⊥CD,
∴∠ACD=90°,
∴tan∠ADC===.
故答案为:.
18.解:∵∠B=90°,sin∠ACB=,
∴=,
∵AB=2,
∴AC=6,
∵AC⊥CD,
∴∠ACD=90°,
∴AD===10,
∴cos∠ADC==.
故答案为:.
19.解:作CD⊥AB的延长线于D,
∵∠ABC=120°,
∴∠CBD=60°,
∵BC=2,
∴DC=BC sin60°=2 =3,
∵tan∠A=,
∴AD=6,
∴AC==3,
∴AO=,
∵OP=,
∴AP=2或.
故答案为2或.
三.解答题(共10小题,满分63分)
20.解:
(1)过点A作AD⊥BC于点D,
∵∠B=30°,
∴cos∠B==,
∴BD=AB,
∵△ABC是等腰三角形,
∴BC=2BD=AB,
故can30°==;
(2)过点A作AE⊥BC于点E,
∵canB=,则可设BC=8x,AB=5x,
∴AE==3x,
∵S△ABC=24,
∴BC×AE=12x2=24,
解得:x=,
故AB=AC=5,BC=8,
从而可得△ABC的周长为18.
21.解:(1)∵absinC=acsinB,
∴bsinC=csinB,
∴=,
:同理得:=,
∴==;
(2)由题意得:∠B=15°,∠C=60°,AB=20,
∴,即,
∴,
∴AC≈40×0.3=12;
(3)由题意得:∠ABC=90°﹣75°=15°,∠ACB=90°﹣45°=45°,
∠A=180°﹣15°﹣45°=120°,
由==得:=,
∴AC≈6,
∴S△ABC=AC×BC×sin∠ACB≈×6×18×0.7≈38.
22.解:==,理由为:
过A作AD⊥BC,BE⊥AC,
在Rt△ABD中,sinB=,即AD=csinB,
在Rt△ADC中,sinC=,即AD=bsinC,
∴csinB=bsinC,即=,
同理可得=,
则==.
23.解:作BE⊥l于点E,DF⊥l于点F.
根据题意,得BE=24mm,DF=48mm.
在Rt△ABE中,sin
,
∴mm
在Rt△ADF中,cos
,
∴mm.
∴矩形ABCD的周长=2(40+60)=200mm.
24.解:在Rt△ACD中,sin∠C=,则AD=bsin∠C,
故答案为:,bsin∠C;
如图2,在△ABC中,∠B=75°,∠C=45°,BC=2,
则∠A=60°,
∵,
∴,
即,
解得,AB=,
即AB的长是.
25.解:如图2,设CD=CA=a,则AD=a,
∵∠B=22.5°,∠ADC=45°,
∴∠DAB=22.5°,
∴∠DAB=∠B,
∴DB=DA=a,
∴BC=BD+CD=(+1)a,
在Rt△ABC中,tanB===﹣1,
即tan22.5°=﹣1;
故答案为﹣1;﹣1;
如图3,延长BA到D,使AD=AB,则AB=AD=AC,
∴∠D=∠ACD,
∵∠CAB=∠D+∠ACD=30°,
∴∠D=15°,
作CH⊥AB于H,设CH=x,则AC=2x,AH=x,
∴AD=AC=2x,
∴DH=AD+AH=(2+)x,
在Rt△DCH中,tanD===2﹣,
即tan15°=2﹣.
26.解:过点B作BM⊥FD于点M,
在△ACB中,∠ACB=90°,∠A=45°,AC=12,
∴BC=AC=12
∵AB∥CF,
∴BM=BC×sin45°=12×=12
CM=BM=12,
在△EFD中,∠F=90°,∠E=30°,
∴∠EDF=60°,
∴MD=BM÷tan60°=4,
∴CD=CM﹣MD=12﹣4.
27.解:∵DE⊥AB于E,
∴tanB==,
设DE=x,
∴BE=2x,
∴BD==,
∴cosB==,
∵∠C=90°,∴cosB===,
∵D是BC边的中点,∴BC=2BD=2,
∴AB=,
∵AE=7,
∴AB=AE+BE,
5x=7+2x,
x=.
故DE=.
28.解:(1)根据正对定义,
当顶角为60°时,等腰三角形底角为60°,
则三角形为等边三角形,
则sad60°==1.
故答案为:1.
(2)当∠A接近0°时,sadA接近0,
当∠A接近180°时,等腰三角形的底接近于腰的二倍,故sadA接近2.
于是sadA的取值范围是0<sadA<2.
故答案为0<sadA<2.
(3)如图,过B作BD⊥AC于D.
在Rt△ABD中,cosA==.
设AD=4k,AB=5k,则BD=3k,
∴DC=5k﹣4k=k.
在Rt△BDC中,BC==k,
∴sadA==.
29.解:(1)作AH⊥BC,垂足为H,
∵AB=AC=5,∴BH=BC=4,
在△ABH中,AH==3,
∴.
(2)作DE⊥BC,垂足为E,
在△BDE中,sinB=,令DE=3k,
BD=5k,则BE==4k,
又在△CDE中,tan∠BCD=,
则CE==6k,
于是BC=BE+EC,即4k+6k=8,
解得,
∴.
