2021-2022学年鲁教版九年级数学上册2.4解直角三角形同步训练(含答案)
文档属性
| 名称 | 2021-2022学年鲁教版九年级数学上册2.4解直角三角形同步训练(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 462.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 09:31:17 | ||
图片预览



文档简介
2021-2022学年鲁教版九年级数学上册《2.4解直角三角形》同步优生辅导训练(附答案)
一、选择题
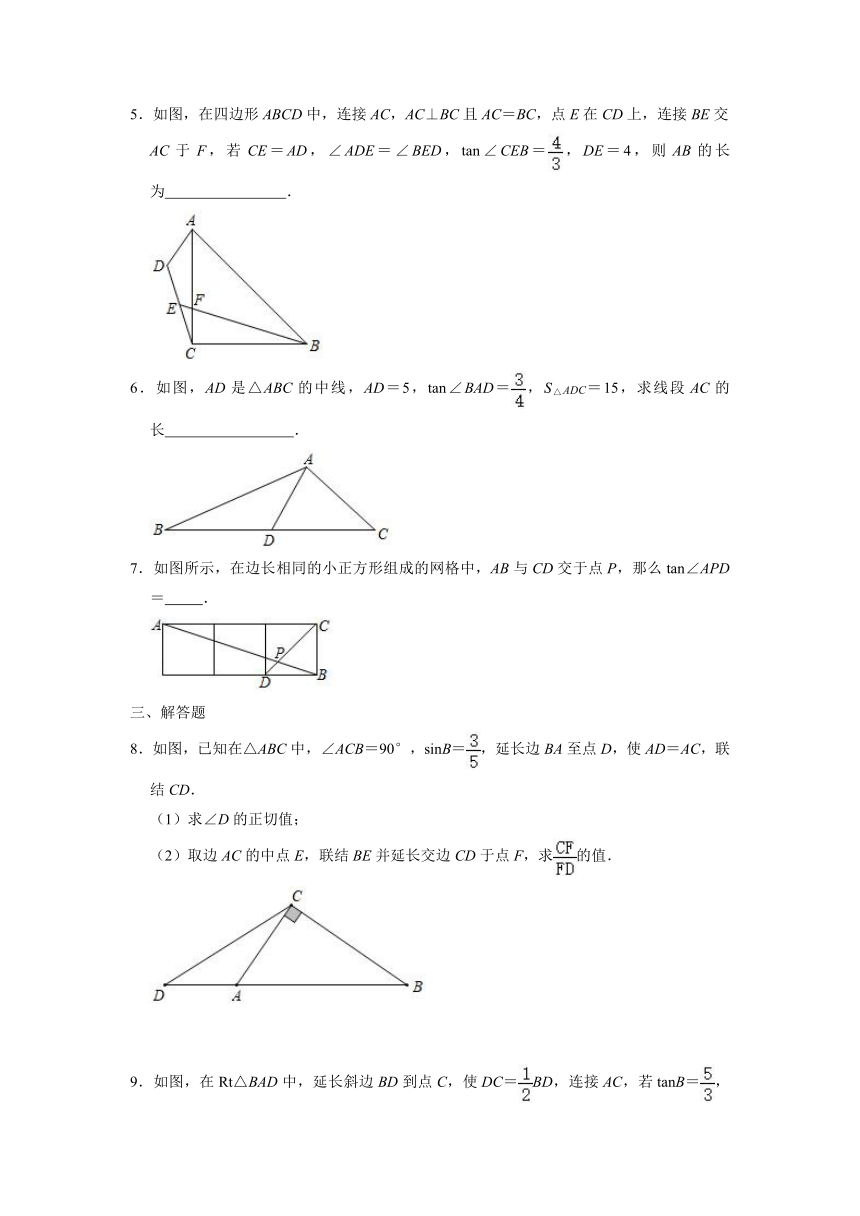
1.如图,AC垂直于AB,P为线段AC上的动点,F为PD的中点,AC=2.8m,PD=2.4m,CF=1.2m,∠DPE=15°.若∠PEB=90°,∠EBA=65°,则AP的长约为( )(参考数据:sin65°≈0.91,cos65°≈0.42,sin50°≈0.77,cos50°≈0.64)
A.1.2
B.1.3m
C.1.5m
D.2.0m
2.如图,在△ABC中,∠ABC=90°,D为BC的中点,点E在AB上,AD,CE交于点F,AE=EF=4,FC=9,则cos∠ACB的值为( )
A.
B.
C.
D.
二、填空题
3.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F,若AC=6,tanB=,则CE=
.
4.如图,在△ABC中,∠ABC=120°,AB=12,点D在边AC上,点E在边BC上,sin∠ADE=,ED=5,如果△ECD的面积是6,那么BC的长是
.
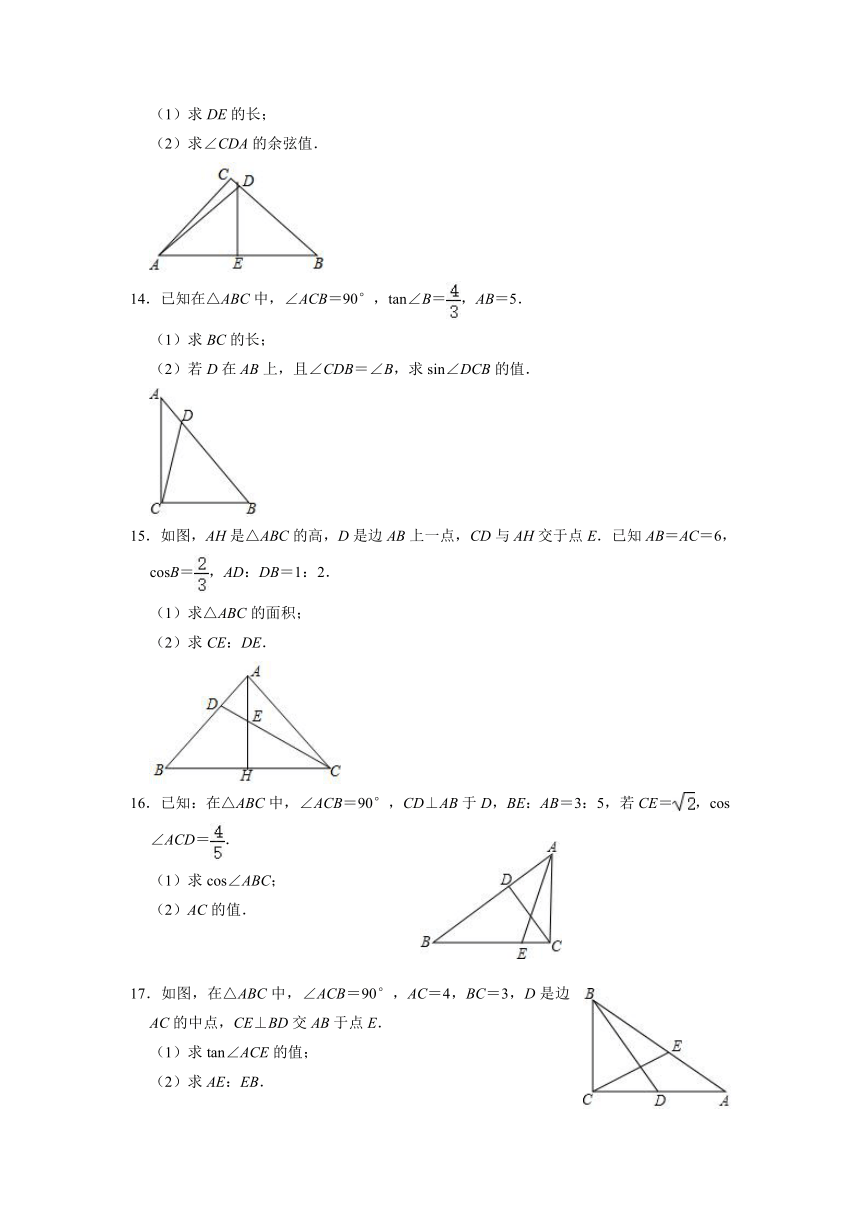
5.如图,在四边形ABCD中,连接AC,AC⊥BC且AC=BC,点E在CD上,连接BE交AC于F,若CE=AD,∠ADE=∠BED,tan∠CEB=,DE=4,则AB的长为
.
6.如图,AD是△ABC的中线,AD=5,tan∠BAD=,S△ADC=15,求线段AC的长
.
7.如图所示,在边长相同的小正方形组成的网格中,AB与CD交于点P,那么tan∠APD=
.
三、解答题
8.如图,已知在△ABC中,∠ACB=90°,sinB=,延长边BA至点D,使AD=AC,联结CD.
(1)求∠D的正切值;
(2)取边AC的中点E,联结BE并延长交边CD于点F,求的值.
9.如图,在Rt△BAD中,延长斜边BD到点C,使DC=BD,连接AC,若tanB=,求tan∠CAD的值.
10.如图,在△ABD中,AC⊥BD于点C,,点E是AB的中点,tanD=2,CE=1,求sin∠ECB的值和AD的长.
11.已知:如图,在△ABC中,AB=13,AC=8,cos∠BAC=,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
(1)求∠EAD的余切值;
(2)求的值.
12.如图,在等腰三角形ABC中,AB=AC,点D在BA的延长线上,BC=24,sin∠ABC=.
(1)求AB的长;
(2)若AD=6.5,求∠DCB的余切值.
13.如图,在Rt△ABC中,∠C=90°,点D在边BC上,DE⊥AB,点E为垂足,AB=7,∠DAB=45°,tanB=.
(1)求DE的长;
(2)求∠CDA的余弦值.
14.已知在△ABC中,∠ACB=90°,tan∠B=,AB=5.
(1)求BC的长;
(2)若D在AB上,且∠CDB=∠B,求sin∠DCB的值.
15.如图,AH是△ABC的高,D是边AB上一点,CD与AH交于点E.已知AB=AC=6,cosB=,AD:DB=1:2.
(1)求△ABC的面积;
(2)求CE:DE.
16.已知:在△ABC中,∠ACB=90°,CD⊥AB于D,BE:AB=3:5,若CE=,cos∠ACD=.
(1)求cos∠ABC;
(2)AC的值.
17.如图,在△ABC中,∠ACB=90°,AC=4,BC=3,D是边AC的中点,CE⊥BD交AB于点E.
(1)求tan∠ACE的值;
(2)求AE:EB.
18.如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD,sin∠ABO==4,求S△BOC的值.
19.如图,△ABC中,∠ACB=90°,D、E分别在AC、BC边上,BE=AD,AE、BD相交于点F,且tan∠AFD=,若AE=13,BD=15,则AD的长为
.
20.如图,在以A为直角顶点的等腰直角三角形纸片ABC中,将B角折起,使点B落在AC边上的点D(不与点A,C重合)处,折痕是EF.
如图1,当CD=AC时,tanα1=;
如图2,当CD=AC时,tanα2=;
如图3,当CD=AC时,tanα3=;
……
依此类推,当CD=AC时,tanα6=
.
参考答案
1.解:如图,过点F作FG⊥AC于点G,
根据题意可知:
当太阳光线与PE垂直时,遮阳效果最佳,
∴∠BEP=90°,
∵∠A=90°,∠B=65°,
∴∠EPA=360°﹣90°﹣90°﹣65°=115°,
∵∠DPE=15°,
∴∠APD=130°,
∴∠CPF=50°,
∵F为PD的中点,
∴DF=PF=PD=1.2(m),
∴CF=PF=1.2(m),
∴CP=2PG=2×PF cos50°≈2×1.2×0.64≈1.53,
∴AP=AC﹣PC=2.8﹣1.53≈1.3(m).
所以要遮阳效果最佳AP的长约为1.3米.
故选:B.
2.解:如图,延长AD到M,使得DM=DF,连接BM.
∵BD=DC,∠BDM=∠CDF,DM=DF,
∴△BDM≌△CDF(SAS),
∴CF=BM=9,∠M=∠CFD,
∵CE∥BM,
∴∠AFE=∠M,
∵EA=EF,
∴∠EAF=∠EFA,
∴∠BAM=∠M,
∴AB=BM=9,
∵AE=4,
∴BE=5,
∵∠EBC=90°,
∴BC===12,
∴AC===15,
∴cos∠ACB===,
解法二:过点D作DG平行AC,构造三角形BDG相似于三角形BCG,同理AEF相似于AGD,再由题目条件,可得cos角ACB的值,遇到分点问题想平行,构造A或8字型相似.
故选:D.
3.解:过点F作FG⊥AB于点G,
∵∠ACB=90°,CD⊥AB,
∴∠CDA=90°,
∴∠CAF+∠CFA=90°,∠FAD+∠AED=90°,
∵AF平分∠CAB,
∴∠CAF=∠FAD,
∴∠CFA=∠AED=∠CEF,
∴CE=CF,
∵AF平分∠CAB,∠ACF=∠AGF=90°,
∴FC=FG,
∵∠B=∠B,∠FGB=∠ACB=90°,
∴△BFG∽△BAC,
∴=,
∵AC=6,∠ACB=90°,
∴tanB==
∴BC=8,AB===10,
∴=,
∵FC=FG,
解得:FC=3,
即CE的长为3.
故答案为:3.
4.解:如图,过点E作EF⊥BC于F,过点A作AH⊥CB交CB的延长线于H.
∵∠ABC=120°,
∴∠ABH=180°﹣∠ABC=60°,
∵AB=12,∠H=90°,
∴BH=AB cos60°=6,AH=AB sin60°=6,
∵EF⊥DF,DE=5,
∴sin∠ADE==,
∴EF=4,
∴DF===3,
∵S△CDE=6,
∴ CD EF=6,
∴CD=3,
∴CF=CD+DF=6,
∵tanC==,
∴=,
∴CH=9,
∴BC=CH﹣BH=9﹣6.
故答案为:9﹣6.
5.解:如图,过点A作AM⊥CD交CD的延长线于点M,过点B作BN⊥DC交DC的延长线于点N,设AD=5x.
∵∠M=∠N=∠ACB=90°,
∴∠ACM+∠BCN=90°,∠CBN+∠BCN=90°,
∴∠ACM=∠CBN,
∵AC=CB,
∴△ACM≌△BCN(AAS),
∴AM=CN,CM=BN,
∵∠ADE=∠BED,
∴∠ADM=∠BEC,
∴tan∠ADM=tan∠BEC==,
∵AD=5x,
∴AM=CN=4x,DM=3x,
∴CM=NB=8x+4,
∵tan∠BEN=,
∴=,
∴x=1,
∴CN=4,BN=12,
∴BC===4,
∴AB=BC=8.
故答案为8.
6.解:过点D作DE⊥AB,垂足为D,过点A作AF⊥DC,垂足为F,
在Rt△ADE中,
∵AD=5,tan∠BAD=,
∵AE=4,DE=3,
∴AD==5,
又∵AD是△ABC的中线,
∴S△ADC=15=S△ADB=AB DE,
∴×3×AB=15,
∴AB=10,BE=AB﹣AE=10﹣4=6,
在Rt△BDE中,BD===3=CD,
由S△ADC=15=CD AF,可得AF=2,
在Rt△ADF中,DF===,
∴FC=CD﹣DF=3﹣=2,
在Rt△AFC中,AF=FC=2,
∴AC=DF=2,
故答案为:2.
7.解:如图,连接BE,交CD于F.
∵四边形BCED是正方形,
∴DF=CF=CD,BF=BE,CD=BE,BE⊥CD,
∴BF=CF,
根据题意得:AC∥BD,
∴△ACP∽△BDP,
∴DP:CP=BD:AC=1:3,
∴DP:DF=1:2,
∴DP=PF=CF=BF,
在Rt△PBF中,tan∠BPF==2,
∵∠APD=∠BPF,
∴tan∠APD=2.
故答案为2.
8.解:(1)过点C作CG⊥AB,垂足为G,
∵∠ACB=90°,
∴∠ACG=∠B,
在△ABC中,sinB=,设AC=3x,则AB=5x,BC=4x,
∴sin∠ACG===sinB,
∴AG=x,CG=x,
∴DG=DA+AG=3x+x=x,
在Rt△DCG中,tan∠D==;
(2)过点C作CH∥DB,交BF的延长线于点H,则有△CHF∽△DBF,
又有E是AC的中点,可证△CHE≌△ABE,
∴HC=AB=5x,
由△CHF∽△DBF得:===.
9.解:如图,作CE⊥AD,
∴∠CED=90°
又∵∠BAD=90°,∠ADB=∠CDE
∴△CDE∽△BDA,
∵DC=BD
∴===,
∵tan
B=,
∴设AD=5x,则AB=3x,
∴CE=x,DE=x,
∴tan∠CAD==.
10.解:∵AC⊥BD,
∴∠ACB=∠ACD=90°.
∵点E是AB的中点,CE=1,
∴BE=CE=1,AB=2CE=2,
∴∠B=∠ECB.
∵=,
∴设BC=3x,CD=2x.
在Rt△ACD中,tanD=2,
∴=2,
∴AC=4x.在Rt△ACB中,
由勾股定理得AB==5x,
∴sin∠ECB=sinB==.
由AB=2,得x=,
∴AD===2x=2×=.
11.解:(1)∵BD⊥AC,
∴∠ADE=90°,
Rt△ADB中,AB=13,cos∠BAC=,
∴AD=5,
由勾股定理得:BD=12,
∵E是BD的中点,
∴ED=6,
∴∠EAD的余切==;
(2)过D作DG∥AF交BC于G,
∵AC=8,AD=5,
∴CD=3,
∵DG∥AF,
∴=,
设CG=3x,FG=5x,
∵EF∥DG,BE=ED,
∴BF=FG=5x,
∴==.
12.解:(1)过点A作AE⊥BC,垂足为点E,
又∵AB=AC,
∴BE=BC,
∵BC=24,
∴BE=12,
在Rt△ABE中,∠AEB=90°,sin∠ABC==,
设AE=5k,AB=13k,
∵AB2=AE2+BE2,
∴BE=12k=12,
∴k=1,
∴AE=5k=5,AB=13k=13;
(2)过点D作DF⊥BC,垂足为点F,
∵AD=6.5,AB=13,
∴BD=AB+AD=19.5,
∵AE⊥BC,DF⊥BC,
∴∠AEB=∠DFB=90°,
∴AE∥DF,
∴==,
又∵AE=5,BE=12,AB=13,
∴DF=,BF=18,
∴CF=BC﹣BF,即CF=24﹣18=6,
在Rt△DCF中,∠DFC=90°,cot∠DCB===.
13.解:(1)∵DE⊥AB,
∴∠DEA=90°,
又∵∠DAB=45°,
∴DE=AE,
在Rt△DEB中,∠DEB=90°,tanB=,
∴=,
设DE=3x,那么AE=3x,BE=4x,
∵AB=7,
∴3x+4x=7,
解得:x=1,
∴DE=3;
(2)在Rt△ADE中,由勾股定理,得AD=3,同理得BD=5,
在Rt△ABC中,由tanB=,可得cosB=,
∴BC=,
∴CD=,
∴cos∠CDA==,即∠CDA的余弦值为.
14.解:(1)∵tan∠B=,
∴,
∴,
∵AC2+BC2=AB2,
∴,
∴BC=3,
(2)过D点作DE⊥BC,则tan∠B=,
∴,
∴,
∵∠CDB=∠B,
∴CD=CB=3,
∵CD2=CE2+DE2,
∴,
∴DE=,
∴sin∠DCB=.
15.解:(1)∵AB=AC=6,cosB=,AH是△ABC的高,
∴BH=4,
∴BC=2BH=8,AH=,
∴△ABC的面积是;==8;
(2)作DF⊥BC于点F,
∵DF⊥BH,AH⊥BH,
∴DF∥AH,
∴,,
∵AD:DB=1:2,BH=CH,
∴AD:AB=1:3,
∴,
∴,
即CE:DE=3:1.
16.解:(1)在Rt△ACD与Rt△ABC中,
∵∠ABC+∠CAD=90°,∠ACD+∠CAD=90°,
∴∠ABC=∠ACD,
∴cos∠ABC=cos∠ACD=
(2)在Rt△ABC中,,令BC=4k,AB=5k,
则AC=3k,
由BE:AB=3:5,
知BE=3k,
则CE=k,且CE=,
则k=,AC=3.
17.解:(1)由∠ACB=90°,CE⊥BD,
得∠ACE=∠CBD
在△BCD中,BC=3,CD=AC=2,∠BCD=90°,
得tan∠CBD=,
即tan∠ACE=,
(2)过A作AC的垂线交CE的延长线于P,
则在△CAP中,CA=4,∠CAP=90°,tan∠ACP=,
得AP=,
又∠ACB=90°,∠CAP=90°,得BC∥AP,
得AE:EB=AP:BC=8:9.
18.解:∵AB⊥AC,CD⊥BD,
∴∠BAC=∠BDC=90°,
又∵∠AOB=∠DOC,
∴△AOB∽△DOC,
∴=,
∴=,
又∵∠AOD=∠BOC,
∴△AOD∽△BOC,
∵∠BAC=90°,sin∠ABO=,
∴=,
∵△AOD∽△BOC,
∴=()2,
∵S△AOD=4,
∴=,
∴S△BOC=9.
19.解:过点A,B作BC,AE的平行线交于点M,连接DM,作DN⊥BM于点N,
则四边形AMBE为平行四边形,
∴∠AFD=∠DBN,
∴tan∠DBN=tan∠AFD==.
设DN=4x,BN=3x,
则BD==5x,
∴5x=15,
解得x=3,
∴DN=4x=12,BN=3x=9,
∵BM=AE=13,
∴MN=BM﹣BN=4,
∴DM===4.
∵BC∥AM,∠C=90°,
∴∠CAM=90°,
∵BE=AD,BE=AM,
∴△DAM为等腰直角三角形,
∴∠MDA=∠DMA=45°,
∴sin45°==,
∴AD=AM=BE=DM=4,
故答案为:4.
20.解:根据规律可得,
当n=2时,CD=AC,tanα1==
当n=3时,CD=AC,tanα2==,
当n=4时,CD=AC,tanα3==,
………………
当n=7时,CD=AC,tanα6==,
故答案为:.
一、选择题
1.如图,AC垂直于AB,P为线段AC上的动点,F为PD的中点,AC=2.8m,PD=2.4m,CF=1.2m,∠DPE=15°.若∠PEB=90°,∠EBA=65°,则AP的长约为( )(参考数据:sin65°≈0.91,cos65°≈0.42,sin50°≈0.77,cos50°≈0.64)
A.1.2
B.1.3m
C.1.5m
D.2.0m
2.如图,在△ABC中,∠ABC=90°,D为BC的中点,点E在AB上,AD,CE交于点F,AE=EF=4,FC=9,则cos∠ACB的值为( )
A.
B.
C.
D.
二、填空题
3.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F,若AC=6,tanB=,则CE=
.
4.如图,在△ABC中,∠ABC=120°,AB=12,点D在边AC上,点E在边BC上,sin∠ADE=,ED=5,如果△ECD的面积是6,那么BC的长是
.
5.如图,在四边形ABCD中,连接AC,AC⊥BC且AC=BC,点E在CD上,连接BE交AC于F,若CE=AD,∠ADE=∠BED,tan∠CEB=,DE=4,则AB的长为
.
6.如图,AD是△ABC的中线,AD=5,tan∠BAD=,S△ADC=15,求线段AC的长
.
7.如图所示,在边长相同的小正方形组成的网格中,AB与CD交于点P,那么tan∠APD=
.
三、解答题
8.如图,已知在△ABC中,∠ACB=90°,sinB=,延长边BA至点D,使AD=AC,联结CD.
(1)求∠D的正切值;
(2)取边AC的中点E,联结BE并延长交边CD于点F,求的值.
9.如图,在Rt△BAD中,延长斜边BD到点C,使DC=BD,连接AC,若tanB=,求tan∠CAD的值.
10.如图,在△ABD中,AC⊥BD于点C,,点E是AB的中点,tanD=2,CE=1,求sin∠ECB的值和AD的长.
11.已知:如图,在△ABC中,AB=13,AC=8,cos∠BAC=,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
(1)求∠EAD的余切值;
(2)求的值.
12.如图,在等腰三角形ABC中,AB=AC,点D在BA的延长线上,BC=24,sin∠ABC=.
(1)求AB的长;
(2)若AD=6.5,求∠DCB的余切值.
13.如图,在Rt△ABC中,∠C=90°,点D在边BC上,DE⊥AB,点E为垂足,AB=7,∠DAB=45°,tanB=.
(1)求DE的长;
(2)求∠CDA的余弦值.
14.已知在△ABC中,∠ACB=90°,tan∠B=,AB=5.
(1)求BC的长;
(2)若D在AB上,且∠CDB=∠B,求sin∠DCB的值.
15.如图,AH是△ABC的高,D是边AB上一点,CD与AH交于点E.已知AB=AC=6,cosB=,AD:DB=1:2.
(1)求△ABC的面积;
(2)求CE:DE.
16.已知:在△ABC中,∠ACB=90°,CD⊥AB于D,BE:AB=3:5,若CE=,cos∠ACD=.
(1)求cos∠ABC;
(2)AC的值.
17.如图,在△ABC中,∠ACB=90°,AC=4,BC=3,D是边AC的中点,CE⊥BD交AB于点E.
(1)求tan∠ACE的值;
(2)求AE:EB.
18.如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD,sin∠ABO==4,求S△BOC的值.
19.如图,△ABC中,∠ACB=90°,D、E分别在AC、BC边上,BE=AD,AE、BD相交于点F,且tan∠AFD=,若AE=13,BD=15,则AD的长为
.
20.如图,在以A为直角顶点的等腰直角三角形纸片ABC中,将B角折起,使点B落在AC边上的点D(不与点A,C重合)处,折痕是EF.
如图1,当CD=AC时,tanα1=;
如图2,当CD=AC时,tanα2=;
如图3,当CD=AC时,tanα3=;
……
依此类推,当CD=AC时,tanα6=
.
参考答案
1.解:如图,过点F作FG⊥AC于点G,
根据题意可知:
当太阳光线与PE垂直时,遮阳效果最佳,
∴∠BEP=90°,
∵∠A=90°,∠B=65°,
∴∠EPA=360°﹣90°﹣90°﹣65°=115°,
∵∠DPE=15°,
∴∠APD=130°,
∴∠CPF=50°,
∵F为PD的中点,
∴DF=PF=PD=1.2(m),
∴CF=PF=1.2(m),
∴CP=2PG=2×PF cos50°≈2×1.2×0.64≈1.53,
∴AP=AC﹣PC=2.8﹣1.53≈1.3(m).
所以要遮阳效果最佳AP的长约为1.3米.
故选:B.
2.解:如图,延长AD到M,使得DM=DF,连接BM.
∵BD=DC,∠BDM=∠CDF,DM=DF,
∴△BDM≌△CDF(SAS),
∴CF=BM=9,∠M=∠CFD,
∵CE∥BM,
∴∠AFE=∠M,
∵EA=EF,
∴∠EAF=∠EFA,
∴∠BAM=∠M,
∴AB=BM=9,
∵AE=4,
∴BE=5,
∵∠EBC=90°,
∴BC===12,
∴AC===15,
∴cos∠ACB===,
解法二:过点D作DG平行AC,构造三角形BDG相似于三角形BCG,同理AEF相似于AGD,再由题目条件,可得cos角ACB的值,遇到分点问题想平行,构造A或8字型相似.
故选:D.
3.解:过点F作FG⊥AB于点G,
∵∠ACB=90°,CD⊥AB,
∴∠CDA=90°,
∴∠CAF+∠CFA=90°,∠FAD+∠AED=90°,
∵AF平分∠CAB,
∴∠CAF=∠FAD,
∴∠CFA=∠AED=∠CEF,
∴CE=CF,
∵AF平分∠CAB,∠ACF=∠AGF=90°,
∴FC=FG,
∵∠B=∠B,∠FGB=∠ACB=90°,
∴△BFG∽△BAC,
∴=,
∵AC=6,∠ACB=90°,
∴tanB==
∴BC=8,AB===10,
∴=,
∵FC=FG,
解得:FC=3,
即CE的长为3.
故答案为:3.
4.解:如图,过点E作EF⊥BC于F,过点A作AH⊥CB交CB的延长线于H.
∵∠ABC=120°,
∴∠ABH=180°﹣∠ABC=60°,
∵AB=12,∠H=90°,
∴BH=AB cos60°=6,AH=AB sin60°=6,
∵EF⊥DF,DE=5,
∴sin∠ADE==,
∴EF=4,
∴DF===3,
∵S△CDE=6,
∴ CD EF=6,
∴CD=3,
∴CF=CD+DF=6,
∵tanC==,
∴=,
∴CH=9,
∴BC=CH﹣BH=9﹣6.
故答案为:9﹣6.
5.解:如图,过点A作AM⊥CD交CD的延长线于点M,过点B作BN⊥DC交DC的延长线于点N,设AD=5x.
∵∠M=∠N=∠ACB=90°,
∴∠ACM+∠BCN=90°,∠CBN+∠BCN=90°,
∴∠ACM=∠CBN,
∵AC=CB,
∴△ACM≌△BCN(AAS),
∴AM=CN,CM=BN,
∵∠ADE=∠BED,
∴∠ADM=∠BEC,
∴tan∠ADM=tan∠BEC==,
∵AD=5x,
∴AM=CN=4x,DM=3x,
∴CM=NB=8x+4,
∵tan∠BEN=,
∴=,
∴x=1,
∴CN=4,BN=12,
∴BC===4,
∴AB=BC=8.
故答案为8.
6.解:过点D作DE⊥AB,垂足为D,过点A作AF⊥DC,垂足为F,
在Rt△ADE中,
∵AD=5,tan∠BAD=,
∵AE=4,DE=3,
∴AD==5,
又∵AD是△ABC的中线,
∴S△ADC=15=S△ADB=AB DE,
∴×3×AB=15,
∴AB=10,BE=AB﹣AE=10﹣4=6,
在Rt△BDE中,BD===3=CD,
由S△ADC=15=CD AF,可得AF=2,
在Rt△ADF中,DF===,
∴FC=CD﹣DF=3﹣=2,
在Rt△AFC中,AF=FC=2,
∴AC=DF=2,
故答案为:2.
7.解:如图,连接BE,交CD于F.
∵四边形BCED是正方形,
∴DF=CF=CD,BF=BE,CD=BE,BE⊥CD,
∴BF=CF,
根据题意得:AC∥BD,
∴△ACP∽△BDP,
∴DP:CP=BD:AC=1:3,
∴DP:DF=1:2,
∴DP=PF=CF=BF,
在Rt△PBF中,tan∠BPF==2,
∵∠APD=∠BPF,
∴tan∠APD=2.
故答案为2.
8.解:(1)过点C作CG⊥AB,垂足为G,
∵∠ACB=90°,
∴∠ACG=∠B,
在△ABC中,sinB=,设AC=3x,则AB=5x,BC=4x,
∴sin∠ACG===sinB,
∴AG=x,CG=x,
∴DG=DA+AG=3x+x=x,
在Rt△DCG中,tan∠D==;
(2)过点C作CH∥DB,交BF的延长线于点H,则有△CHF∽△DBF,
又有E是AC的中点,可证△CHE≌△ABE,
∴HC=AB=5x,
由△CHF∽△DBF得:===.
9.解:如图,作CE⊥AD,
∴∠CED=90°
又∵∠BAD=90°,∠ADB=∠CDE
∴△CDE∽△BDA,
∵DC=BD
∴===,
∵tan
B=,
∴设AD=5x,则AB=3x,
∴CE=x,DE=x,
∴tan∠CAD==.
10.解:∵AC⊥BD,
∴∠ACB=∠ACD=90°.
∵点E是AB的中点,CE=1,
∴BE=CE=1,AB=2CE=2,
∴∠B=∠ECB.
∵=,
∴设BC=3x,CD=2x.
在Rt△ACD中,tanD=2,
∴=2,
∴AC=4x.在Rt△ACB中,
由勾股定理得AB==5x,
∴sin∠ECB=sinB==.
由AB=2,得x=,
∴AD===2x=2×=.
11.解:(1)∵BD⊥AC,
∴∠ADE=90°,
Rt△ADB中,AB=13,cos∠BAC=,
∴AD=5,
由勾股定理得:BD=12,
∵E是BD的中点,
∴ED=6,
∴∠EAD的余切==;
(2)过D作DG∥AF交BC于G,
∵AC=8,AD=5,
∴CD=3,
∵DG∥AF,
∴=,
设CG=3x,FG=5x,
∵EF∥DG,BE=ED,
∴BF=FG=5x,
∴==.
12.解:(1)过点A作AE⊥BC,垂足为点E,
又∵AB=AC,
∴BE=BC,
∵BC=24,
∴BE=12,
在Rt△ABE中,∠AEB=90°,sin∠ABC==,
设AE=5k,AB=13k,
∵AB2=AE2+BE2,
∴BE=12k=12,
∴k=1,
∴AE=5k=5,AB=13k=13;
(2)过点D作DF⊥BC,垂足为点F,
∵AD=6.5,AB=13,
∴BD=AB+AD=19.5,
∵AE⊥BC,DF⊥BC,
∴∠AEB=∠DFB=90°,
∴AE∥DF,
∴==,
又∵AE=5,BE=12,AB=13,
∴DF=,BF=18,
∴CF=BC﹣BF,即CF=24﹣18=6,
在Rt△DCF中,∠DFC=90°,cot∠DCB===.
13.解:(1)∵DE⊥AB,
∴∠DEA=90°,
又∵∠DAB=45°,
∴DE=AE,
在Rt△DEB中,∠DEB=90°,tanB=,
∴=,
设DE=3x,那么AE=3x,BE=4x,
∵AB=7,
∴3x+4x=7,
解得:x=1,
∴DE=3;
(2)在Rt△ADE中,由勾股定理,得AD=3,同理得BD=5,
在Rt△ABC中,由tanB=,可得cosB=,
∴BC=,
∴CD=,
∴cos∠CDA==,即∠CDA的余弦值为.
14.解:(1)∵tan∠B=,
∴,
∴,
∵AC2+BC2=AB2,
∴,
∴BC=3,
(2)过D点作DE⊥BC,则tan∠B=,
∴,
∴,
∵∠CDB=∠B,
∴CD=CB=3,
∵CD2=CE2+DE2,
∴,
∴DE=,
∴sin∠DCB=.
15.解:(1)∵AB=AC=6,cosB=,AH是△ABC的高,
∴BH=4,
∴BC=2BH=8,AH=,
∴△ABC的面积是;==8;
(2)作DF⊥BC于点F,
∵DF⊥BH,AH⊥BH,
∴DF∥AH,
∴,,
∵AD:DB=1:2,BH=CH,
∴AD:AB=1:3,
∴,
∴,
即CE:DE=3:1.
16.解:(1)在Rt△ACD与Rt△ABC中,
∵∠ABC+∠CAD=90°,∠ACD+∠CAD=90°,
∴∠ABC=∠ACD,
∴cos∠ABC=cos∠ACD=
(2)在Rt△ABC中,,令BC=4k,AB=5k,
则AC=3k,
由BE:AB=3:5,
知BE=3k,
则CE=k,且CE=,
则k=,AC=3.
17.解:(1)由∠ACB=90°,CE⊥BD,
得∠ACE=∠CBD
在△BCD中,BC=3,CD=AC=2,∠BCD=90°,
得tan∠CBD=,
即tan∠ACE=,
(2)过A作AC的垂线交CE的延长线于P,
则在△CAP中,CA=4,∠CAP=90°,tan∠ACP=,
得AP=,
又∠ACB=90°,∠CAP=90°,得BC∥AP,
得AE:EB=AP:BC=8:9.
18.解:∵AB⊥AC,CD⊥BD,
∴∠BAC=∠BDC=90°,
又∵∠AOB=∠DOC,
∴△AOB∽△DOC,
∴=,
∴=,
又∵∠AOD=∠BOC,
∴△AOD∽△BOC,
∵∠BAC=90°,sin∠ABO=,
∴=,
∵△AOD∽△BOC,
∴=()2,
∵S△AOD=4,
∴=,
∴S△BOC=9.
19.解:过点A,B作BC,AE的平行线交于点M,连接DM,作DN⊥BM于点N,
则四边形AMBE为平行四边形,
∴∠AFD=∠DBN,
∴tan∠DBN=tan∠AFD==.
设DN=4x,BN=3x,
则BD==5x,
∴5x=15,
解得x=3,
∴DN=4x=12,BN=3x=9,
∵BM=AE=13,
∴MN=BM﹣BN=4,
∴DM===4.
∵BC∥AM,∠C=90°,
∴∠CAM=90°,
∵BE=AD,BE=AM,
∴△DAM为等腰直角三角形,
∴∠MDA=∠DMA=45°,
∴sin45°==,
∴AD=AM=BE=DM=4,
故答案为:4.
20.解:根据规律可得,
当n=2时,CD=AC,tanα1==
当n=3时,CD=AC,tanα2==,
当n=4时,CD=AC,tanα3==,
………………
当n=7时,CD=AC,tanα6==,
故答案为:.
