2021-2022学年人教版八年级数学上册12.2 全等三角形的判定(1) 课后作业(word版、含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册12.2 全等三角形的判定(1) 课后作业(word版、含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 264.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 00:00:00 | ||
图片预览

文档简介
12.2
三角形全等的判定(1)
1.下列命题正确的是( )
A.
三条边对应相等的两个三角形全等
B.
周长相等的两个三角形全等
C.
三个角对应相等的两个三角形全等
D.
面积相等的两个三角形全等
2.如图,在△ACE和△BDF中,AE=BF,CE=DF,要利用“SSS”证明△ACE≌△BDF,需增加的一个条件是( )
A.
AB=BC
B.
DC=BC
C.
AB=CD
D.
以上都不对
3.
如图KH12-9-1,AB=FD,AC=FE,BD=CE,则△ABC和△FDE( )
A.
一定全等
B.
一定不全等
C.
可能全等
D.
上述三种情况都有可能
4.如图KH12-9-2,在△ABC中,AB=AC,EB=EC,则直接由“SSS”可以判定( )
A.
△ABD≌△ACD
B.
△ABE≌△ACE
C.
△BDE≌△CDE
D.
以上答案都不对
5.如图KH12-9-3,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )
A.
120°
B.
125°
C.
127°
D.
104°
6.我国的纸伞工艺十分巧妙.
如图KH12-9-4,伞不论张开还是收拢,伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC,从而保证伞圈D能沿着伞柄滑动.
为了证明这个结论,我们的依据是( )
A.
SSS
B.
SAS
C.
AAS
D.
ASA
7.如图,AB=CD,AD=CB,判定△ABD≌△CDB的依据是( )
A.
SSS
B.
ASA
C.
SAS
D.
AAS
8.如图,用尺规作∠A′O′B′=∠AOB的依据是( )
A.
SAS
B.
ASA
C.
AAS
D.
SSS
9.如图,已知AB=DC,AC=DB,BE=CE,则∠A=__________.
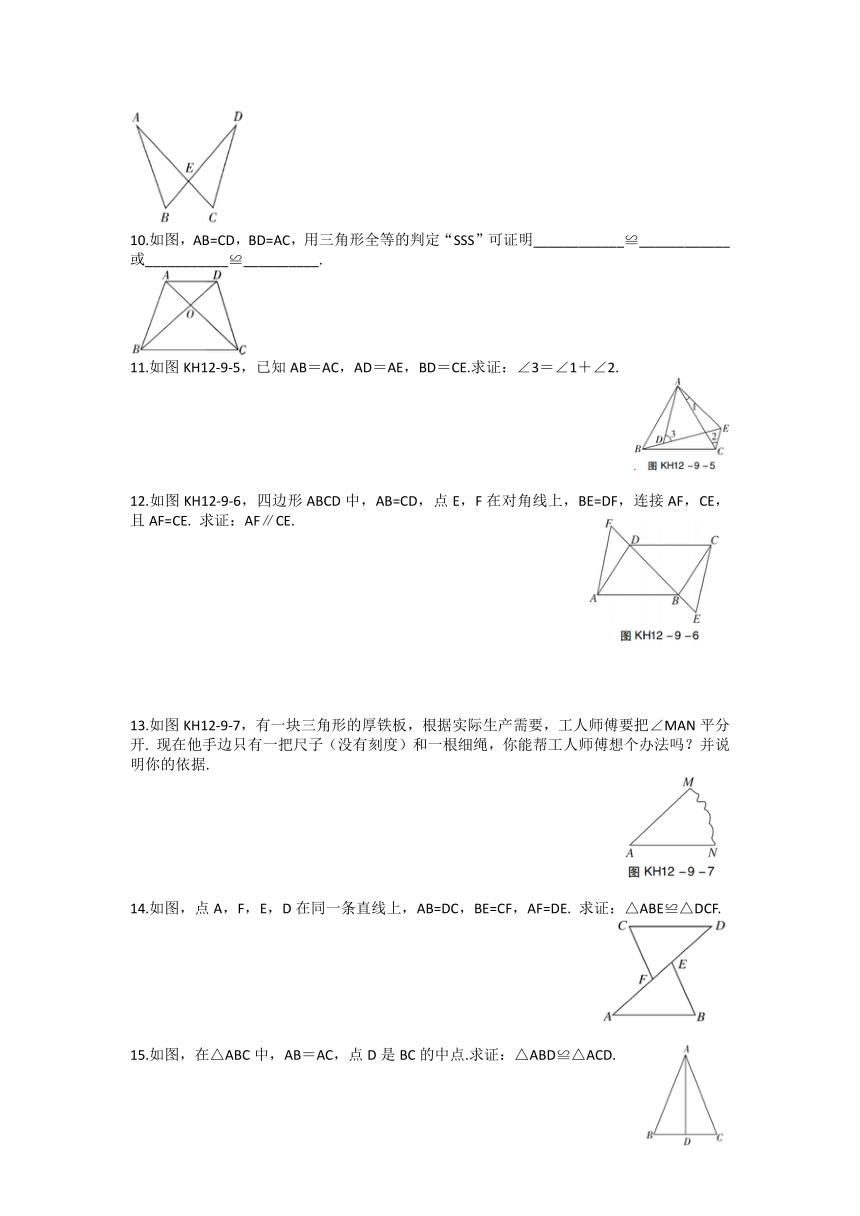
10.如图,AB=CD,BD=AC,用三角形全等的判定“SSS”可证明____________≌____________或___________≌__________.
11.如图KH12-9-5,已知AB=AC,AD=AE,BD=CE.求证:∠3=∠1+∠2.
12.如图KH12-9-6,四边形ABCD中,AB=CD,点E,F在对角线上,BE=DF,连接AF,CE,且AF=CE.
求证:AF∥CE.
13.如图KH12-9-7,有一块三角形的厚铁板,根据实际生产需要,工人师傅要把∠MAN平分开.
现在他手边只有一把尺子(没有刻度)和一根细绳,你能帮工人师傅想个办法吗?并说明你的依据.
14.如图,点A,F,E,D在同一条直线上,AB=DC,BE=CF,AF=DE.
求证:△ABE≌△DCF.
15.如图,在△ABC中,AB=AC,点D是BC的中点.求证:△ABD≌△ACD.
参考答案
1——8
ACABCAAD
9.∠D
10.△ABC
△ACD
△ABD
△DCA
11.
证明:在△ABD和△ACE中,
∴△ABD≌△ACE(SSS).
∴∠ABD=∠2,∠BAD=∠1.
∵∠3=∠BAD+∠ABD,
∴∠3=∠1+∠2.
12.
证明:∵DF=BE,
∴DF+BD=BE+BD,
即BF=DE.
∵AB=CD,AF=CE,
∴△ABF≌△CDE(SSS).
∴∠F=∠E.
∴AF∥CE.
13.
解:用绳子的一定长度以A为圆心画弧,分别交AM,AN于B,C两点,再以B,C两点为圆心,大于BC长为半径画弧,两弧交于D点,作射线AD,则AD平分∠MAN.依据如下.
如图.AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD(SSS).
∴∠BAD=∠CAD.
∴AD为∠MAN的平分线.
14.
证明:∵AF=DE,∴AF+EF=DE+EF,
即AE=DF.
在△ABE和△DCF中,
∴△ABE≌△DCF(SSS).
15.
证明:∵点D是BC的中点,∴BD=CD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS).
三角形全等的判定(1)
1.下列命题正确的是( )
A.
三条边对应相等的两个三角形全等
B.
周长相等的两个三角形全等
C.
三个角对应相等的两个三角形全等
D.
面积相等的两个三角形全等
2.如图,在△ACE和△BDF中,AE=BF,CE=DF,要利用“SSS”证明△ACE≌△BDF,需增加的一个条件是( )
A.
AB=BC
B.
DC=BC
C.
AB=CD
D.
以上都不对
3.
如图KH12-9-1,AB=FD,AC=FE,BD=CE,则△ABC和△FDE( )
A.
一定全等
B.
一定不全等
C.
可能全等
D.
上述三种情况都有可能
4.如图KH12-9-2,在△ABC中,AB=AC,EB=EC,则直接由“SSS”可以判定( )
A.
△ABD≌△ACD
B.
△ABE≌△ACE
C.
△BDE≌△CDE
D.
以上答案都不对
5.如图KH12-9-3,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )
A.
120°
B.
125°
C.
127°
D.
104°
6.我国的纸伞工艺十分巧妙.
如图KH12-9-4,伞不论张开还是收拢,伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC,从而保证伞圈D能沿着伞柄滑动.
为了证明这个结论,我们的依据是( )
A.
SSS
B.
SAS
C.
AAS
D.
ASA
7.如图,AB=CD,AD=CB,判定△ABD≌△CDB的依据是( )
A.
SSS
B.
ASA
C.
SAS
D.
AAS
8.如图,用尺规作∠A′O′B′=∠AOB的依据是( )
A.
SAS
B.
ASA
C.
AAS
D.
SSS
9.如图,已知AB=DC,AC=DB,BE=CE,则∠A=__________.
10.如图,AB=CD,BD=AC,用三角形全等的判定“SSS”可证明____________≌____________或___________≌__________.
11.如图KH12-9-5,已知AB=AC,AD=AE,BD=CE.求证:∠3=∠1+∠2.
12.如图KH12-9-6,四边形ABCD中,AB=CD,点E,F在对角线上,BE=DF,连接AF,CE,且AF=CE.
求证:AF∥CE.
13.如图KH12-9-7,有一块三角形的厚铁板,根据实际生产需要,工人师傅要把∠MAN平分开.
现在他手边只有一把尺子(没有刻度)和一根细绳,你能帮工人师傅想个办法吗?并说明你的依据.
14.如图,点A,F,E,D在同一条直线上,AB=DC,BE=CF,AF=DE.
求证:△ABE≌△DCF.
15.如图,在△ABC中,AB=AC,点D是BC的中点.求证:△ABD≌△ACD.
参考答案
1——8
ACABCAAD
9.∠D
10.△ABC
△ACD
△ABD
△DCA
11.
证明:在△ABD和△ACE中,
∴△ABD≌△ACE(SSS).
∴∠ABD=∠2,∠BAD=∠1.
∵∠3=∠BAD+∠ABD,
∴∠3=∠1+∠2.
12.
证明:∵DF=BE,
∴DF+BD=BE+BD,
即BF=DE.
∵AB=CD,AF=CE,
∴△ABF≌△CDE(SSS).
∴∠F=∠E.
∴AF∥CE.
13.
解:用绳子的一定长度以A为圆心画弧,分别交AM,AN于B,C两点,再以B,C两点为圆心,大于BC长为半径画弧,两弧交于D点,作射线AD,则AD平分∠MAN.依据如下.
如图.AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD(SSS).
∴∠BAD=∠CAD.
∴AD为∠MAN的平分线.
14.
证明:∵AF=DE,∴AF+EF=DE+EF,
即AE=DF.
在△ABE和△DCF中,
∴△ABE≌△DCF(SSS).
15.
证明:∵点D是BC的中点,∴BD=CD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS).
