2021-2022学年人教版八年级数学上册12.2 全等三角形的判定(2) 课后作业(word版、含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册12.2 全等三角形的判定(2) 课后作业(word版、含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 310.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 09:22:03 | ||
图片预览

文档简介
12.2
全等三角形的判定(2)
1.如图,已知AD⊥BC,D是BC的中点,则△ABD≌△ACD的依据是( )
A.
SSS
B.
ASA
C.
SAS
D.
AAS
2.如图,已知AB=AC,AD=AE,∠BAC=∠DAE,则下列结论不正确的是( )
A.
∠BAD=∠CAE
B.
△ABD≌△ACE
C.
AB=BC
D.
BD=CE
3.如图,∠1=∠2,要证明△ABC≌△ADE,还需补充的条件是( )
A.
AB=AD,AC=AE
B.
AB=AD,BC=DE
C.
AC=AE,BC=DE
D.
以上都不对
4.如图,AB=AC,添加下列条件,能用SAS判断△ABE≌△ACD的是( )
A.
∠B=∠C
B.
∠AEB=∠ADC
C.
AE=AD
D.
BE=CD
5.如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠AEC的度数为( )
A.
60°
B.
50°
C.
45°
D.
30°
6.如图,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定D,使CD=BC,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是( )
A.
AAS
B.
SAS
C.
ASA
D.
SSS
7.如图,要用“SAS”证明△ABC≌△ADE,若已知AB=AD,AC=AE,则还需添加条件( )
A.
∠BAE=∠DAC
B.
∠B=∠D
C.
∠C=∠E
D.
∠1=∠2
8.
如图,AB=CD,∠ABD=∠CDB,判定△ABD≌△CDB的依据是( )
A.
SAS
B.
ASA
C.
SSS
D.
AAS
9.如图,有一池塘,要测池塘两端A,B间的距离,可先在平地上取一个不经过池塘可以直接到达点A和B的点C,连接AC并延长至点D,使CD=CA,连接BC并延长至点E,使CE=CB,连接ED.
若量出DE的长度为58
m,则A,B间的距离即可求出.
依据是( )
A.
SAS
B.
SSS
C.
AAS
D.
ASA
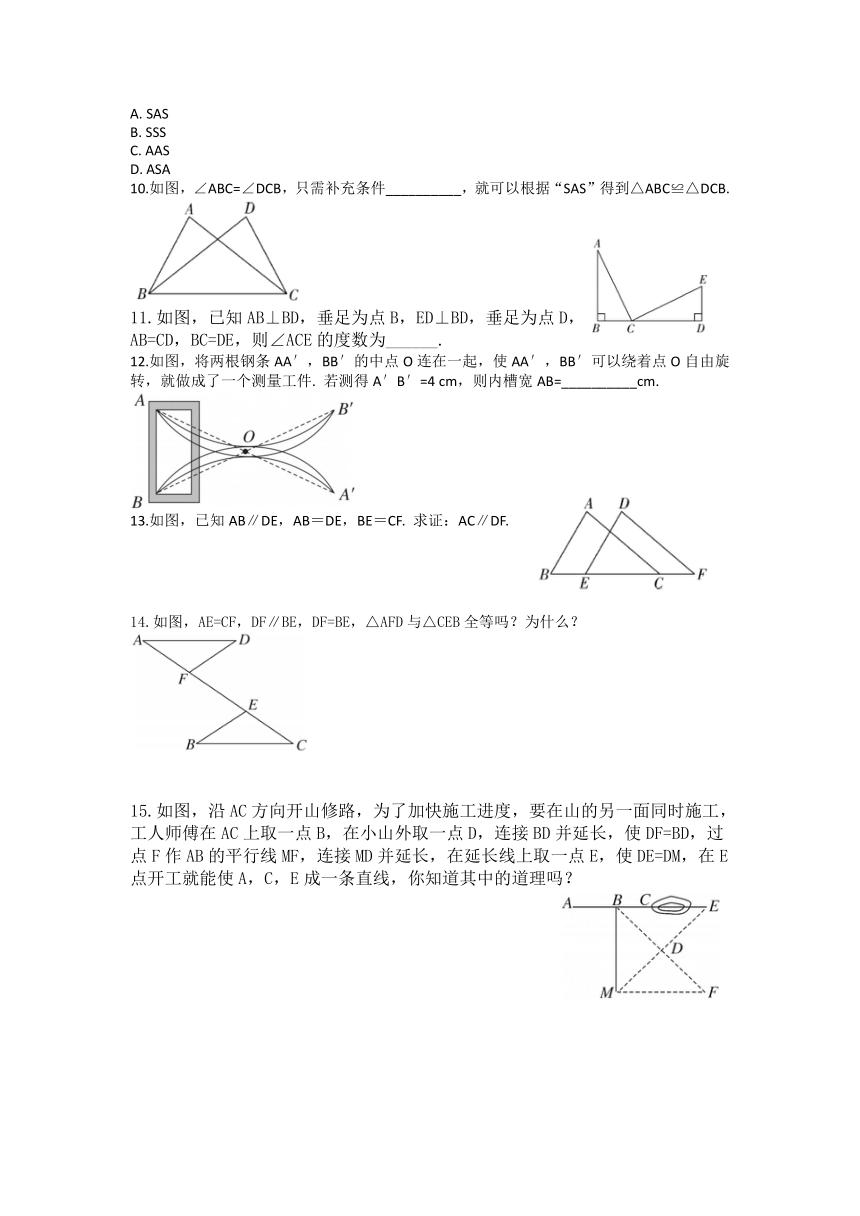
10.如图,∠ABC=∠DCB,只需补充条件__________,就可以根据“SAS”得到△ABC≌△DCB.
11.如图,已知AB⊥BD,垂足为点B,ED⊥BD,垂足为点D,AB=CD,BC=DE,则∠ACE的度数为______.
12.如图,将两根钢条AA′,BB′的中点O连在一起,使AA′,BB′可以绕着点O自由旋转,就做成了一个测量工件.
若测得A′B′=4
cm,则内槽宽AB=__________cm.
13.如图,已知AB∥DE,AB=DE,BE=CF.
求证:AC∥DF.
14.如图,AE=CF,DF∥BE,DF=BE,△AFD与△CEB全等吗?为什么?
15.如图,沿AC方向开山修路,为了加快施工进度,要在山的另一面同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD并延长,使DF=BD,过点F作AB的平行线MF,连接MD并延长,在延长线上取一点E,使DE=DM,在E点开工就能使A,C,E成一条直线,你知道其中的道理吗?
参考答案
1——9
CCACABAAA
10.AB=DC
11.90°
12.4
13.
证明:∵AB∥DE,∴∠B=∠DEF.
∵BE=CF,∴BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS).
∴∠ACB=∠F.∴AC∥DF.
14.
解:全等.理由如下.
∵AE=CF,
∴AF=CE.
∵DF∥BE,
∴∠DFE=∠BEF.
∴∠AFD=∠CEB.
在△AFD和△CEB中,
∴△AFD≌△CEB(SAS).
15.
解:∵在△BDE和△FDM中,
∴△BDE≌△FDM(SAS).
∴∠BEM=∠FME.
∴BE∥MF.
∵AB∥MF,
∴A,C,E三点在一条直线上.
全等三角形的判定(2)
1.如图,已知AD⊥BC,D是BC的中点,则△ABD≌△ACD的依据是( )
A.
SSS
B.
ASA
C.
SAS
D.
AAS
2.如图,已知AB=AC,AD=AE,∠BAC=∠DAE,则下列结论不正确的是( )
A.
∠BAD=∠CAE
B.
△ABD≌△ACE
C.
AB=BC
D.
BD=CE
3.如图,∠1=∠2,要证明△ABC≌△ADE,还需补充的条件是( )
A.
AB=AD,AC=AE
B.
AB=AD,BC=DE
C.
AC=AE,BC=DE
D.
以上都不对
4.如图,AB=AC,添加下列条件,能用SAS判断△ABE≌△ACD的是( )
A.
∠B=∠C
B.
∠AEB=∠ADC
C.
AE=AD
D.
BE=CD
5.如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠AEC的度数为( )
A.
60°
B.
50°
C.
45°
D.
30°
6.如图,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定D,使CD=BC,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是( )
A.
AAS
B.
SAS
C.
ASA
D.
SSS
7.如图,要用“SAS”证明△ABC≌△ADE,若已知AB=AD,AC=AE,则还需添加条件( )
A.
∠BAE=∠DAC
B.
∠B=∠D
C.
∠C=∠E
D.
∠1=∠2
8.
如图,AB=CD,∠ABD=∠CDB,判定△ABD≌△CDB的依据是( )
A.
SAS
B.
ASA
C.
SSS
D.
AAS
9.如图,有一池塘,要测池塘两端A,B间的距离,可先在平地上取一个不经过池塘可以直接到达点A和B的点C,连接AC并延长至点D,使CD=CA,连接BC并延长至点E,使CE=CB,连接ED.
若量出DE的长度为58
m,则A,B间的距离即可求出.
依据是( )
A.
SAS
B.
SSS
C.
AAS
D.
ASA
10.如图,∠ABC=∠DCB,只需补充条件__________,就可以根据“SAS”得到△ABC≌△DCB.
11.如图,已知AB⊥BD,垂足为点B,ED⊥BD,垂足为点D,AB=CD,BC=DE,则∠ACE的度数为______.
12.如图,将两根钢条AA′,BB′的中点O连在一起,使AA′,BB′可以绕着点O自由旋转,就做成了一个测量工件.
若测得A′B′=4
cm,则内槽宽AB=__________cm.
13.如图,已知AB∥DE,AB=DE,BE=CF.
求证:AC∥DF.
14.如图,AE=CF,DF∥BE,DF=BE,△AFD与△CEB全等吗?为什么?
15.如图,沿AC方向开山修路,为了加快施工进度,要在山的另一面同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD并延长,使DF=BD,过点F作AB的平行线MF,连接MD并延长,在延长线上取一点E,使DE=DM,在E点开工就能使A,C,E成一条直线,你知道其中的道理吗?
参考答案
1——9
CCACABAAA
10.AB=DC
11.90°
12.4
13.
证明:∵AB∥DE,∴∠B=∠DEF.
∵BE=CF,∴BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS).
∴∠ACB=∠F.∴AC∥DF.
14.
解:全等.理由如下.
∵AE=CF,
∴AF=CE.
∵DF∥BE,
∴∠DFE=∠BEF.
∴∠AFD=∠CEB.
在△AFD和△CEB中,
∴△AFD≌△CEB(SAS).
15.
解:∵在△BDE和△FDM中,
∴△BDE≌△FDM(SAS).
∴∠BEM=∠FME.
∴BE∥MF.
∵AB∥MF,
∴A,C,E三点在一条直线上.
