四川省成都市郫都区2022届高三上学期9月阶段性检测(一)文科数学试题(Word版含答案)
文档属性
| 名称 | 四川省成都市郫都区2022届高三上学期9月阶段性检测(一)文科数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 885.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 23:39:05 | ||
图片预览




文档简介
成都市郫都区2021-2022高三上学期阶段性检测(一)
数
学(文科)
说明:1.本卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,时间120分钟.
所有试题均在答题卡相应的区域内作答.
第I卷(选择题
共60分)
一.选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是最符合题目要求的)
1.已知集合,,那么集合等于
A.
B.
C.
D.
2.复数,则的虚部是
A.
B.
C.
D.
3.为比较甲,乙两名篮球运动员的近期竞技状态,选取这两名球员最近五场的得分制成如图所示的茎叶图.
有下列结论:
①甲最近五场比赛得分的中位数高于乙最近五场比赛得分的中位数;
②甲最近五场比赛得分的平均数低于乙最近五场比赛得分的平均数;
③从最近五场比赛的得分看,乙比甲更稳定;
④从最近五场比赛的得分看,甲比乙更稳定.
其中所有正确结论的序号是
A.②③
B.①④
C.①③
D.②④
4.设计如下图的四个电路图,则能表示“开关A闭合”是“灯泡B亮”的必要不充分条件的一个电路图是
A.
B.
C.
D.
5.2020年,新型冠状病毒引发的疫情牵动着亿万人的心,八方驰援战疫情,众志成城克时难,社会各界支援湖北共抗新型冠状病毒肺炎,成都某医院派出3名医生,2名护士支援湖北,现从这5人中任选2人定点支援湖北某医院,则恰有1名医生和1名护士被选中的概率为
A.
0.7
B.
0.4
C.
0.6
D.
0.3
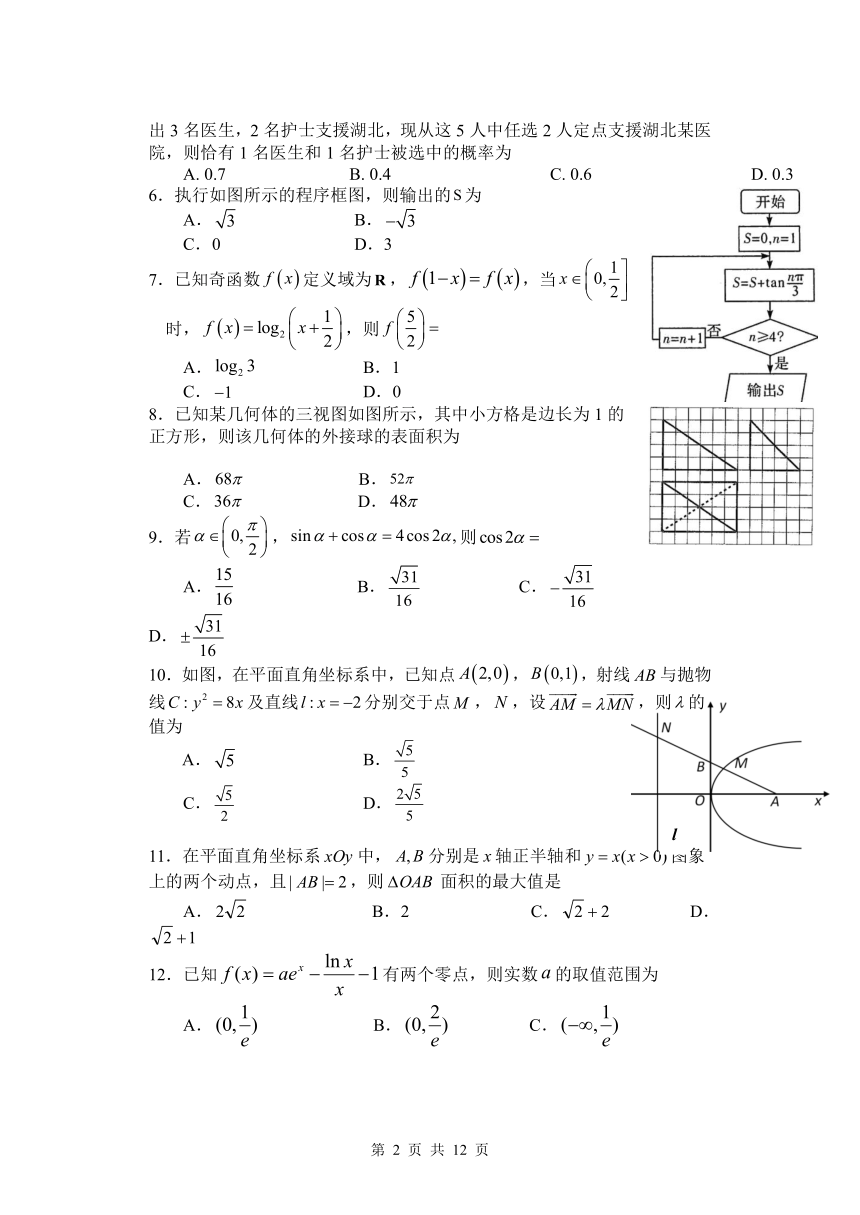
6.执行如图所示的程序框图,则输出的为
A.
B.
C.0
D.3
7.已知奇函数定义域为,,当时,,则
A.
B.1
C.
D.0
8.已知某几何体的三视图如图所示,其中小方格是边长为1的正方形,则该几何体的外接球的表面积为
A.
B.
C.
D.
9.若,则
A.
B.
C.
D.
10.如图,在平面直角坐标系中,已知点,,射线与抛物线及直线分别交于点,,设,则的值为
A.
B.
C.
D.
11.在平面直角坐标系中,分别是轴正半轴和图象上的两个动点,且,则面积的最大值是
A.
B.2
C.
D.
12.已知有两个零点,则实数的取值范围为
A.
B.
C.
D.
第II卷(非选择题
共90分)
注意事项:必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指定的答题区域内作答,作图题可先用铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚,答在试题卷上无效.
二.填空题(本大题共4小题,每小题5分,共20分)
13.已知某产品的销售额与广告费之间的关系如下表:
若根据表中的数据用最小二乘法求得对的回归方程为,则的值是_________.
14.已知双曲线的一条渐近线过点,则的离心率为_________.
15.设,是两个不共线的向量,若向量与的方向相反,则实数________.
16.已知函数,若函数恰好有两个零点,则实数等于_________.
三.解答题(本大题共6小题,共70分.
解答应写出文字说明,证明过程或演算步骤.)
17.(本小题满分12分)
已知是等差数列的前项和,.
从下面的两个条件中任选其中一个:①;②,求解下列问题:
(1)求数列的通项;
(2)设,试比较数列的前项和与的大小.
(注:条件①、②只能任选其一,若两个都选,则以条件①计分)
18.(本小题满分12分)
今年7号台风“查帕卡”在我国沿海登陆,给当地人民造成了巨大的财产损失,适逢暑假,大学生小张调查了当地某小区的户居民由于台风造成的经济损失,将收集的数据分成、、、、五组作出频率分布直方图,如图:
经济损失
不超过元
超过元
合计
捐款超过元
捐款不超过元
合计
(1)台风后居委会号召小区居民为台风重灾区捐款,小张调查的户居民捐款情况如表格,在表格空白处填写正确数字,并说明是否有以上的把握认为捐款数额多于或少于元和自身经济损失是否到元有关?
(2)若损失超过平均数则视为损失严重,求这100户居民大约有多少户损失严重?(结果保留整数)
附:
19.(本小题满分12分)
如图所示的几何体中,是菱形,,平面,,.
(1)求证:平面;
(2)求三棱锥的体积.
20.(本小题满分12分)
已知椭圆,点 分别是其左 右焦点,点A B分别为其左 右顶点.若两焦点与短轴两端点围成四边形面积为,且圆为该四边形的内切圆.
(1)求椭圆C的方程;
(2)若以(1)中较圆的椭圆为研究对象,过的直线交椭圆于两点,求面积的最大值.
21.(本小题满分12分)
已知函数
(1)当时,求在处的切线方程;
(2)若,求实数取值的集合;
(3)当时,对任意,令,证明:.
请考生在22、23题中任选一题作答,共10分,如果多作,则按所作的第一题计分.
作答时,请用2B铅笔在答题卡上将所选题目题号的方框涂黑.
22.(本小题满分10分)选修4-4:坐标系与参数方程
已知直线在平面直角坐标系中经过点,倾斜角,在直角坐标系中,若以为极点,轴正半轴为极轴建立极坐标系.圆C的极坐标方程为.
(1)写出直线的参数方程,并把圆的极坐标方程化为直角坐标系下的普通方程;
(2)设与圆相交于两点,且的中点为,求的长及.
23.(本小题满分10分)
选修4-5:不等式选讲
已知函数,.
(1)画出的图象;
(2)若,求的取值范围.
郫都区2019级一阶数学(文)参考答案
一、选择题:CCAB
CADA
BDDA
二、填空题:13.20
14.
15.
16.
三、解答题:17.解:选①,
(1)设等差数列的公差为,
则即解得:,
…………………2分
所以数列的通项为:,
…………………4分
(2)由等差数列前n项和公式可得:,…………………6分
所以,
…………………8分
数列的前n项
…………………10分
…………………12分
选②,
(1)设等差数列的公差为,
由题意可得:即解得:,
…………………2分
所以数列的通项为:,
…………………4分
(2)同上
18.解:(1)由频率分布直方图可知,在抽取的户中,经济损失不超过元的有户,则经济损失超过元的有户,
则表格数据如下:
经济损失不超过元
经济损失超过元
合计
捐款超过元
捐款不超过元
合计
…………………2分
,
∵,,
∴有以上把握认为捐款数额是否多于或少于元和自身经济损失是否到元有关
…………………6分
(2)平均数为:
元
…………………9分
这100户居民损失严重的有:户
…………………12分
19.(1)证明:,∴
…………………2分
,∴
…………………4分
∵
所以,又所以平面.…………………6分
(2)
…………………12分
20.解:(1)设半焦距为,则即,
又直线与圆相切,∴,
…………………3分
故,∴,故,故,或,,
椭圆方程为或.
…………………5分
(2)较圆的椭圆为
根据题意,直线斜率不为0,设直线,
联立方程得,
…………………7分
…………………9分
令,则
易知单调递增,
所以当时,取最大值,此时.
…………12分
21.解:(1)当时,,,
∴,∴在处的切线方程为
…………3分
(2)当时,在上单调递减,注意到,不符合题意;
…………4分
当时,在上单调递减,在上单调递增.
所以的最小值为
令
所以在(0,1)单调递增,单调递减
所以在有最大值,∴,∴
∴
综上,当时,实数取值的集合为.
…………7分
(3)当时,,则
由(2)知,,当且仅当时取等
①
…………10分
由①式可得当时
…………12分
(第(3)小题也可以直接齐次化构造找函数,在评讲中顺带将对数均值不等式一起复习)
22.解:(1)直线的参数方程为(为参数),即(为参数)
…………………2分
由,得,所以,
得,即.
…………………4分
(2)把(为参数)代入,得,
…………………6分
∴.
…………………8分
.
…………………10分
23.(1)由题可知
,
…………………3分
画出函数图像:
…………………5分
(2),如图,在同一个坐标系里画出图像,
是平移了个单位得到,
则要使,需将向左平移,即,…………………7分
当过时,,解得或(舍去),………………8分
则数形结合可得需至少将向左平移个单位,.…………………10分
数
学(文科)
说明:1.本卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,时间120分钟.
所有试题均在答题卡相应的区域内作答.
第I卷(选择题
共60分)
一.选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是最符合题目要求的)
1.已知集合,,那么集合等于
A.
B.
C.
D.
2.复数,则的虚部是
A.
B.
C.
D.
3.为比较甲,乙两名篮球运动员的近期竞技状态,选取这两名球员最近五场的得分制成如图所示的茎叶图.
有下列结论:
①甲最近五场比赛得分的中位数高于乙最近五场比赛得分的中位数;
②甲最近五场比赛得分的平均数低于乙最近五场比赛得分的平均数;
③从最近五场比赛的得分看,乙比甲更稳定;
④从最近五场比赛的得分看,甲比乙更稳定.
其中所有正确结论的序号是
A.②③
B.①④
C.①③
D.②④
4.设计如下图的四个电路图,则能表示“开关A闭合”是“灯泡B亮”的必要不充分条件的一个电路图是
A.
B.
C.
D.
5.2020年,新型冠状病毒引发的疫情牵动着亿万人的心,八方驰援战疫情,众志成城克时难,社会各界支援湖北共抗新型冠状病毒肺炎,成都某医院派出3名医生,2名护士支援湖北,现从这5人中任选2人定点支援湖北某医院,则恰有1名医生和1名护士被选中的概率为
A.
0.7
B.
0.4
C.
0.6
D.
0.3
6.执行如图所示的程序框图,则输出的为
A.
B.
C.0
D.3
7.已知奇函数定义域为,,当时,,则
A.
B.1
C.
D.0
8.已知某几何体的三视图如图所示,其中小方格是边长为1的正方形,则该几何体的外接球的表面积为
A.
B.
C.
D.
9.若,则
A.
B.
C.
D.
10.如图,在平面直角坐标系中,已知点,,射线与抛物线及直线分别交于点,,设,则的值为
A.
B.
C.
D.
11.在平面直角坐标系中,分别是轴正半轴和图象上的两个动点,且,则面积的最大值是
A.
B.2
C.
D.
12.已知有两个零点,则实数的取值范围为
A.
B.
C.
D.
第II卷(非选择题
共90分)
注意事项:必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指定的答题区域内作答,作图题可先用铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚,答在试题卷上无效.
二.填空题(本大题共4小题,每小题5分,共20分)
13.已知某产品的销售额与广告费之间的关系如下表:
若根据表中的数据用最小二乘法求得对的回归方程为,则的值是_________.
14.已知双曲线的一条渐近线过点,则的离心率为_________.
15.设,是两个不共线的向量,若向量与的方向相反,则实数________.
16.已知函数,若函数恰好有两个零点,则实数等于_________.
三.解答题(本大题共6小题,共70分.
解答应写出文字说明,证明过程或演算步骤.)
17.(本小题满分12分)
已知是等差数列的前项和,.
从下面的两个条件中任选其中一个:①;②,求解下列问题:
(1)求数列的通项;
(2)设,试比较数列的前项和与的大小.
(注:条件①、②只能任选其一,若两个都选,则以条件①计分)
18.(本小题满分12分)
今年7号台风“查帕卡”在我国沿海登陆,给当地人民造成了巨大的财产损失,适逢暑假,大学生小张调查了当地某小区的户居民由于台风造成的经济损失,将收集的数据分成、、、、五组作出频率分布直方图,如图:
经济损失
不超过元
超过元
合计
捐款超过元
捐款不超过元
合计
(1)台风后居委会号召小区居民为台风重灾区捐款,小张调查的户居民捐款情况如表格,在表格空白处填写正确数字,并说明是否有以上的把握认为捐款数额多于或少于元和自身经济损失是否到元有关?
(2)若损失超过平均数则视为损失严重,求这100户居民大约有多少户损失严重?(结果保留整数)
附:
19.(本小题满分12分)
如图所示的几何体中,是菱形,,平面,,.
(1)求证:平面;
(2)求三棱锥的体积.
20.(本小题满分12分)
已知椭圆,点 分别是其左 右焦点,点A B分别为其左 右顶点.若两焦点与短轴两端点围成四边形面积为,且圆为该四边形的内切圆.
(1)求椭圆C的方程;
(2)若以(1)中较圆的椭圆为研究对象,过的直线交椭圆于两点,求面积的最大值.
21.(本小题满分12分)
已知函数
(1)当时,求在处的切线方程;
(2)若,求实数取值的集合;
(3)当时,对任意,令,证明:.
请考生在22、23题中任选一题作答,共10分,如果多作,则按所作的第一题计分.
作答时,请用2B铅笔在答题卡上将所选题目题号的方框涂黑.
22.(本小题满分10分)选修4-4:坐标系与参数方程
已知直线在平面直角坐标系中经过点,倾斜角,在直角坐标系中,若以为极点,轴正半轴为极轴建立极坐标系.圆C的极坐标方程为.
(1)写出直线的参数方程,并把圆的极坐标方程化为直角坐标系下的普通方程;
(2)设与圆相交于两点,且的中点为,求的长及.
23.(本小题满分10分)
选修4-5:不等式选讲
已知函数,.
(1)画出的图象;
(2)若,求的取值范围.
郫都区2019级一阶数学(文)参考答案
一、选择题:CCAB
CADA
BDDA
二、填空题:13.20
14.
15.
16.
三、解答题:17.解:选①,
(1)设等差数列的公差为,
则即解得:,
…………………2分
所以数列的通项为:,
…………………4分
(2)由等差数列前n项和公式可得:,…………………6分
所以,
…………………8分
数列的前n项
…………………10分
…………………12分
选②,
(1)设等差数列的公差为,
由题意可得:即解得:,
…………………2分
所以数列的通项为:,
…………………4分
(2)同上
18.解:(1)由频率分布直方图可知,在抽取的户中,经济损失不超过元的有户,则经济损失超过元的有户,
则表格数据如下:
经济损失不超过元
经济损失超过元
合计
捐款超过元
捐款不超过元
合计
…………………2分
,
∵,,
∴有以上把握认为捐款数额是否多于或少于元和自身经济损失是否到元有关
…………………6分
(2)平均数为:
元
…………………9分
这100户居民损失严重的有:户
…………………12分
19.(1)证明:,∴
…………………2分
,∴
…………………4分
∵
所以,又所以平面.…………………6分
(2)
…………………12分
20.解:(1)设半焦距为,则即,
又直线与圆相切,∴,
…………………3分
故,∴,故,故,或,,
椭圆方程为或.
…………………5分
(2)较圆的椭圆为
根据题意,直线斜率不为0,设直线,
联立方程得,
…………………7分
…………………9分
令,则
易知单调递增,
所以当时,取最大值,此时.
…………12分
21.解:(1)当时,,,
∴,∴在处的切线方程为
…………3分
(2)当时,在上单调递减,注意到,不符合题意;
…………4分
当时,在上单调递减,在上单调递增.
所以的最小值为
令
所以在(0,1)单调递增,单调递减
所以在有最大值,∴,∴
∴
综上,当时,实数取值的集合为.
…………7分
(3)当时,,则
由(2)知,,当且仅当时取等
①
…………10分
由①式可得当时
…………12分
(第(3)小题也可以直接齐次化构造找函数,在评讲中顺带将对数均值不等式一起复习)
22.解:(1)直线的参数方程为(为参数),即(为参数)
…………………2分
由,得,所以,
得,即.
…………………4分
(2)把(为参数)代入,得,
…………………6分
∴.
…………………8分
.
…………………10分
23.(1)由题可知
,
…………………3分
画出函数图像:
…………………5分
(2),如图,在同一个坐标系里画出图像,
是平移了个单位得到,
则要使,需将向左平移,即,…………………7分
当过时,,解得或(舍去),………………8分
则数形结合可得需至少将向左平移个单位,.…………………10分
同课章节目录
