2021-2022学年人教版八年级数学上册12.2 全等三角形的判定(3) 课后作业 (word版、含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册12.2 全等三角形的判定(3) 课后作业 (word版、含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 246.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 09:23:32 | ||
图片预览

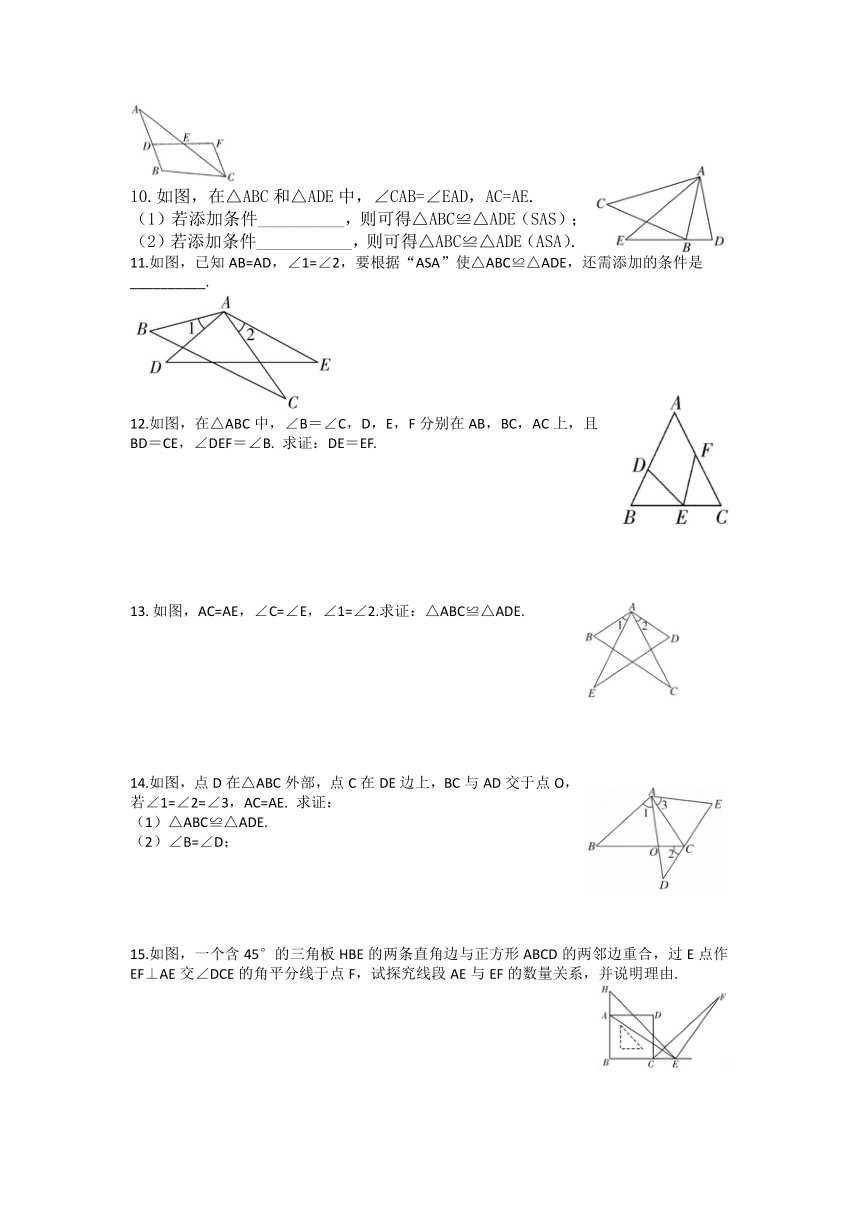
文档简介
12.2
全等三角形的判定(3)
1.
根据已知条件,能画出唯一的△ABC的是
( )
A.
AB=3,BC=4,AC=8
B.
∠A=60°,∠B=45°,AB=4
C.
AB=3,BC=5,∠A=30°
D.
∠C=90°,AB=6
2.下列说法正确的是( )
A.
有两边和一角对应相等的两个三角形全等
B.
有两角和它们的夹边对应相等的两个三角形全等
C.
两个等边三角形一定全等
D.
两个等腰直角三角形一定全等
3.如图,用纸板挡住了三角形的一部分,小明根据所学知识很快就画出了一个与原来完全一样的三角形,他的依据是( )
A.
ASA
B.
SAS
C.
AAS
D.
SSS
4.如图,一块三角形的玻璃打碎成了三块,某同学要到玻璃店配一块与此玻璃形状、大小完全一样的玻璃,最省事的办法是带哪一块去 ( )
A.
①
B.
②
C.
③
D.
不能确定
5.如图,∠1=∠2,∠3=∠4,则判定△ABD和△ACD全等的依据是( )
A.
SSS
B.
ASA
C.
SAS
D.
AAS
6.如图,AE=AC,若要判断△ABC≌△ADE,则不能添加的条件为
( )
A.
DC=BE
B.
AD=AB
C.
DE=BC
D.
∠C=∠E
7.如图,AB=AC,∠B=∠C,BE,CD相交于点O,则直接判定△ABE≌△ACD的依据
是( )
A.
SAS
B.
ASA
C.
SSA
D.
AAA
8.如图,点B,E,C,F在一条直线上,AB∥DE,AC∥DF,下列条件中,能判断△ABC≌△DEF的是( )
A.
BE=CE
B.
∠A=∠D
C.
EC=CF
D.
BE=CF
9.如图,已知AB∥CF,点E为AC的中点,若AB=9
cm,CF=5
cm,则BD的长度为__________cm
10.如图,在△ABC和△ADE中,∠CAB=∠EAD,AC=AE.
(1)若添加条件__________,则可得△ABC≌△ADE(SAS);
(2)若添加条件___________,则可得△ABC≌△ADE(ASA).
11.如图,已知AB=AD,∠1=∠2,要根据“ASA”使△ABC≌△ADE,还需添加的条件是__________.
12.如图,在△ABC中,∠B=∠C,D,E,F分别在AB,BC,AC上,且BD=CE,∠DEF=∠B.
求证:DE=EF.
如图,AC=AE,∠C=∠E,∠1=∠2.求证:△ABC≌△ADE.
14.如图,点D在△ABC外部,点C在DE边上,BC与AD交于点O,若∠1=∠2=∠3,AC=AE.
求证:
(1)△ABC≌△ADE.
(2)∠B=∠D;
15.如图,一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合,过E点作EF⊥AE交∠DCE的角平分线于点F,试探究线段AE与EF的数量关系,并说明理由.
参考答案
1——8
BBACBCBD
9.4
10.(1)AB=AD
(2)∠C=∠E
11.∠B=∠D
12.
证明:∵∠B+∠BDE=∠DEC=∠DEF+∠CEF,
又∵∠B=∠DEF,
∴∠BDE=∠CEF.
又∵∠B=∠C,BD=CE,
∴△BDE≌△CEF(ASA).
∴DE=EF.
13.
证明:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC.
∴∠BAC=∠DAE.
在△ABC和△ADE中,
∴△ABC≌△ADE(ASA).
14.
证明:(1)∵∠1=∠3,
∴∠1+∠DAC=∠3+∠DAC,
即∠BAC=∠DAE.
∵∠E=180°-∠3-∠ACE,
∠ACB=180°-∠2-∠ACE,
∠2=∠3,
∴∠ACB=∠E.
在△ABC与△ADE中,
∴△ABC≌△ADE(ASA).
(2)∵△ABC≌△ADE,
∴∠B=∠D.
15.
解:AE=EF.理由如下.
∵四边形ABCD是正方形,
∴AB=BC.
又∵BH=BE,
∴AH=EC.
∵△HBE为等腰直角三角形,
∴∠H=45°.
∵CF平分∠DCE,∴∠FCE=∠H=45°.
∵AD∥BE,∴∠DAE=∠CEA.
∵AE⊥EF,
∠HAD=90°,
∴∠HAD+∠DAE=∠AEF+∠CEA,即∠HAE=∠CEF.
在△HAE和△CEF中,
∴△HAE≌△CEF(ASA).
∴AE=EF.
全等三角形的判定(3)
1.
根据已知条件,能画出唯一的△ABC的是
( )
A.
AB=3,BC=4,AC=8
B.
∠A=60°,∠B=45°,AB=4
C.
AB=3,BC=5,∠A=30°
D.
∠C=90°,AB=6
2.下列说法正确的是( )
A.
有两边和一角对应相等的两个三角形全等
B.
有两角和它们的夹边对应相等的两个三角形全等
C.
两个等边三角形一定全等
D.
两个等腰直角三角形一定全等
3.如图,用纸板挡住了三角形的一部分,小明根据所学知识很快就画出了一个与原来完全一样的三角形,他的依据是( )
A.
ASA
B.
SAS
C.
AAS
D.
SSS
4.如图,一块三角形的玻璃打碎成了三块,某同学要到玻璃店配一块与此玻璃形状、大小完全一样的玻璃,最省事的办法是带哪一块去 ( )
A.
①
B.
②
C.
③
D.
不能确定
5.如图,∠1=∠2,∠3=∠4,则判定△ABD和△ACD全等的依据是( )
A.
SSS
B.
ASA
C.
SAS
D.
AAS
6.如图,AE=AC,若要判断△ABC≌△ADE,则不能添加的条件为
( )
A.
DC=BE
B.
AD=AB
C.
DE=BC
D.
∠C=∠E
7.如图,AB=AC,∠B=∠C,BE,CD相交于点O,则直接判定△ABE≌△ACD的依据
是( )
A.
SAS
B.
ASA
C.
SSA
D.
AAA
8.如图,点B,E,C,F在一条直线上,AB∥DE,AC∥DF,下列条件中,能判断△ABC≌△DEF的是( )
A.
BE=CE
B.
∠A=∠D
C.
EC=CF
D.
BE=CF
9.如图,已知AB∥CF,点E为AC的中点,若AB=9
cm,CF=5
cm,则BD的长度为__________cm
10.如图,在△ABC和△ADE中,∠CAB=∠EAD,AC=AE.
(1)若添加条件__________,则可得△ABC≌△ADE(SAS);
(2)若添加条件___________,则可得△ABC≌△ADE(ASA).
11.如图,已知AB=AD,∠1=∠2,要根据“ASA”使△ABC≌△ADE,还需添加的条件是__________.
12.如图,在△ABC中,∠B=∠C,D,E,F分别在AB,BC,AC上,且BD=CE,∠DEF=∠B.
求证:DE=EF.
如图,AC=AE,∠C=∠E,∠1=∠2.求证:△ABC≌△ADE.
14.如图,点D在△ABC外部,点C在DE边上,BC与AD交于点O,若∠1=∠2=∠3,AC=AE.
求证:
(1)△ABC≌△ADE.
(2)∠B=∠D;
15.如图,一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合,过E点作EF⊥AE交∠DCE的角平分线于点F,试探究线段AE与EF的数量关系,并说明理由.
参考答案
1——8
BBACBCBD
9.4
10.(1)AB=AD
(2)∠C=∠E
11.∠B=∠D
12.
证明:∵∠B+∠BDE=∠DEC=∠DEF+∠CEF,
又∵∠B=∠DEF,
∴∠BDE=∠CEF.
又∵∠B=∠C,BD=CE,
∴△BDE≌△CEF(ASA).
∴DE=EF.
13.
证明:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC.
∴∠BAC=∠DAE.
在△ABC和△ADE中,
∴△ABC≌△ADE(ASA).
14.
证明:(1)∵∠1=∠3,
∴∠1+∠DAC=∠3+∠DAC,
即∠BAC=∠DAE.
∵∠E=180°-∠3-∠ACE,
∠ACB=180°-∠2-∠ACE,
∠2=∠3,
∴∠ACB=∠E.
在△ABC与△ADE中,
∴△ABC≌△ADE(ASA).
(2)∵△ABC≌△ADE,
∴∠B=∠D.
15.
解:AE=EF.理由如下.
∵四边形ABCD是正方形,
∴AB=BC.
又∵BH=BE,
∴AH=EC.
∵△HBE为等腰直角三角形,
∴∠H=45°.
∵CF平分∠DCE,∴∠FCE=∠H=45°.
∵AD∥BE,∴∠DAE=∠CEA.
∵AE⊥EF,
∠HAD=90°,
∴∠HAD+∠DAE=∠AEF+∠CEA,即∠HAE=∠CEF.
在△HAE和△CEF中,
∴△HAE≌△CEF(ASA).
∴AE=EF.
