2020-2021学年八年级数学人教版上册12.2三角形全等的判定 课后练习 (word版、含解析)
文档属性
| 名称 | 2020-2021学年八年级数学人教版上册12.2三角形全等的判定 课后练习 (word版、含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 586.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 00:00:00 | ||
图片预览


文档简介
三角形全等的判定
一、单选题
1.下列说法正确的个数有(
)
①有一个锐角和它的对边分别相等的两个直角三角形全等;②有两边分别相等的两个直角三角形全等;③有两个锐角和斜边分别相等的两个直角三角形全等.
A.3个
B.2个
C.1个
D.0个
2.如果两个三角形中两条边分别相等,且相等的一对边上的高也相等,那么这两个三角形的第三条边所对的角的关系是(
)
A.相等
B.不相等
C.互余或相等
D.互补或相等
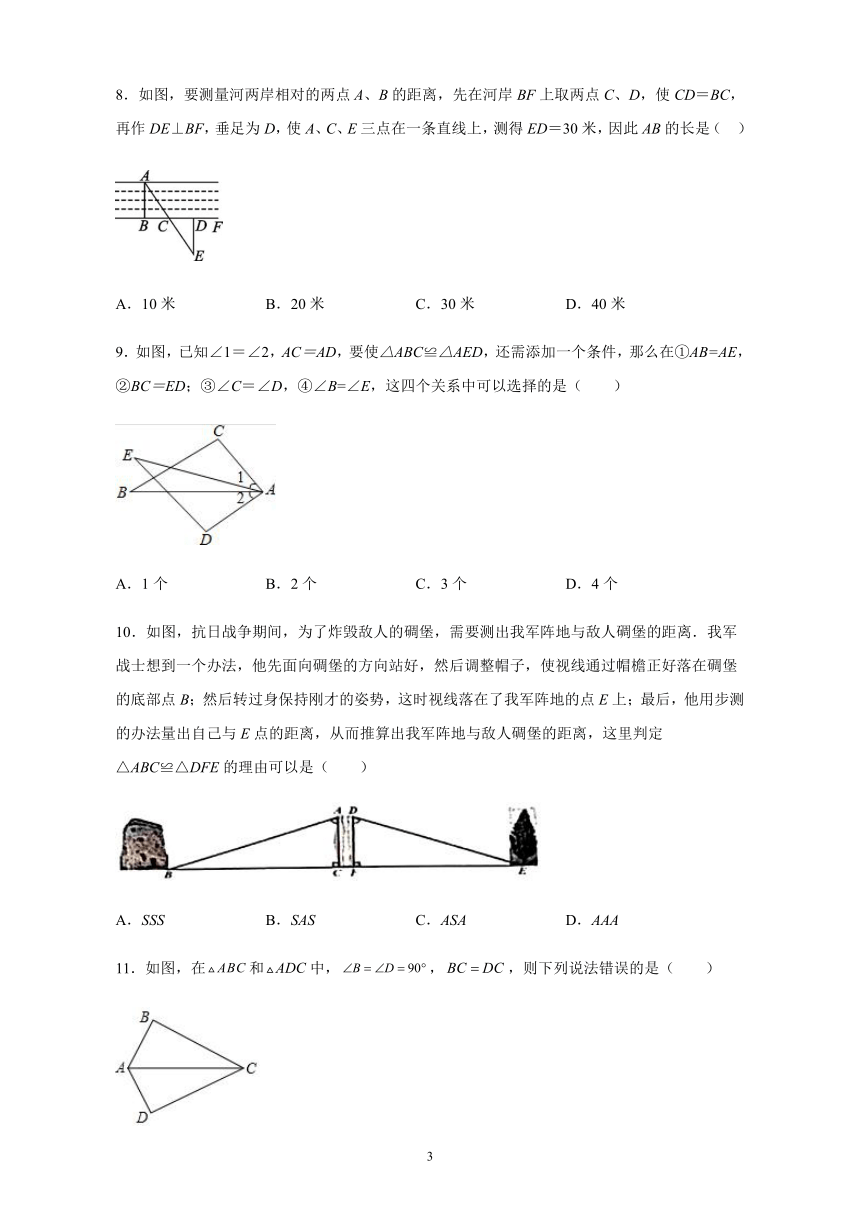
3.如图,在四边形ABCD中,∠ACB=∠DAC,添加一个条件后不能保证△BAC≌△DCA是( )
A.AB∥CD
B.∠B=∠D
C.AB=CD
D.AD=BC
4.如图,已知,用直尺和圆规按照以下步骤作图:
①以点为圆心,任意长为半径画弧,分别交,于点,;
②画射线,以点为圆心,长为半径画弧,交于点;
③以点为圆心,长为半径画弧,与第②步中所画的弧相交于点;
④过点画射线;
根据以上操作,可以判定,其判定的依据是(
)
A.
B.
C.
D.
5.如图所示,是的边上的中线,cm,cm,则边的长度可能是(
)
A.3cm
B.5cm
C.14cm
D.13cm
6.已知:如图,,,要使,需添加一个条件,则添加的条件以及相应的判定定理合适的是(
)
A.
B.
C.
D.
7.如图,已知线段米,于点,米,射线于,点从点向运动,每秒走米,点从点向运动,每秒走米,、同时从出发,则出发秒后,在线段上有一点,使与全等,则的值为(
)
A.
B.
C.或
D.或
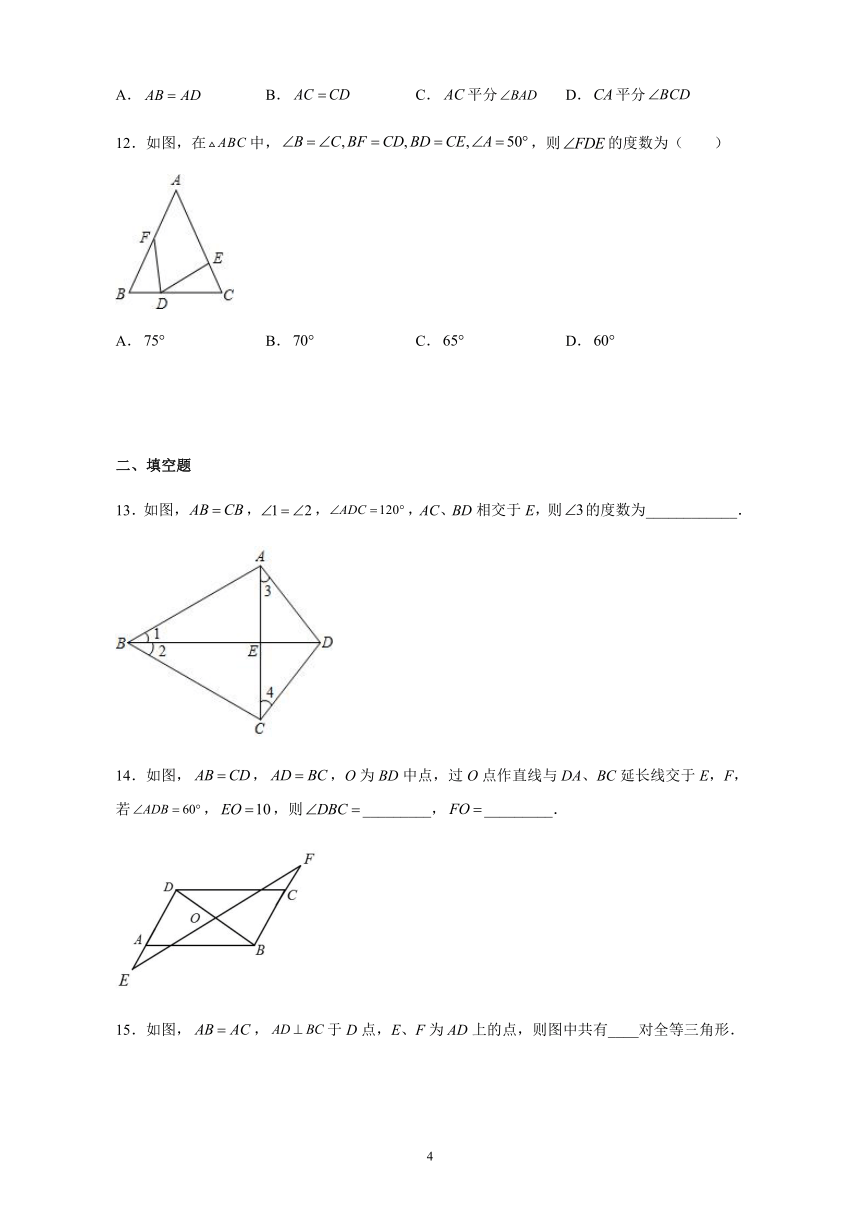
8.如图,要测量河两岸相对的两点A、B的距离,先在河岸BF上取两点C、D,使CD=BC,再作DE⊥BF,垂足为D,使A、C、E三点在一条直线上,测得ED=30米,因此AB的长是(
)
A.10米
B.20米
C.30米
D.40米
9.如图,已知∠1=∠2,AC=AD,要使△ABC≌△AED,还需添加一个条件,那么在①AB=AE,②BC=ED;③∠C=∠D,④∠B=∠E,这四个关系中可以选择的是( )
A.1个
B.2个
C.3个
D.4个
10.如图,抗日战争期间,为了炸毁敌人的碉堡,需要测出我军阵地与敌人碉堡的距离.我军战士想到一个办法,他先面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部点B;然后转过身保持刚才的姿势,这时视线落在了我军阵地的点E上;最后,他用步测的办法量出自己与E点的距离,从而推算出我军阵地与敌人碉堡的距离,这里判定△ABC≌△DFE的理由可以是( )
A.SSS
B.SAS
C.ASA
D.AAA
11.如图,在和中,,,则下列说法错误的是(
)
A.
B.
C.平分
D.平分
12.如图,在中,,则的度数为(
)
A.
B.
C.
D.
二、填空题
13.如图,,,,AC、BD相交于E,则的度数为____________.
14.如图,,,O为BD中点,过O点作直线与DA、BC延长线交于E,F,若,,则_________,_________.
15.如图,,于D点,E、F为AD上的点,则图中共有____对全等三角形.
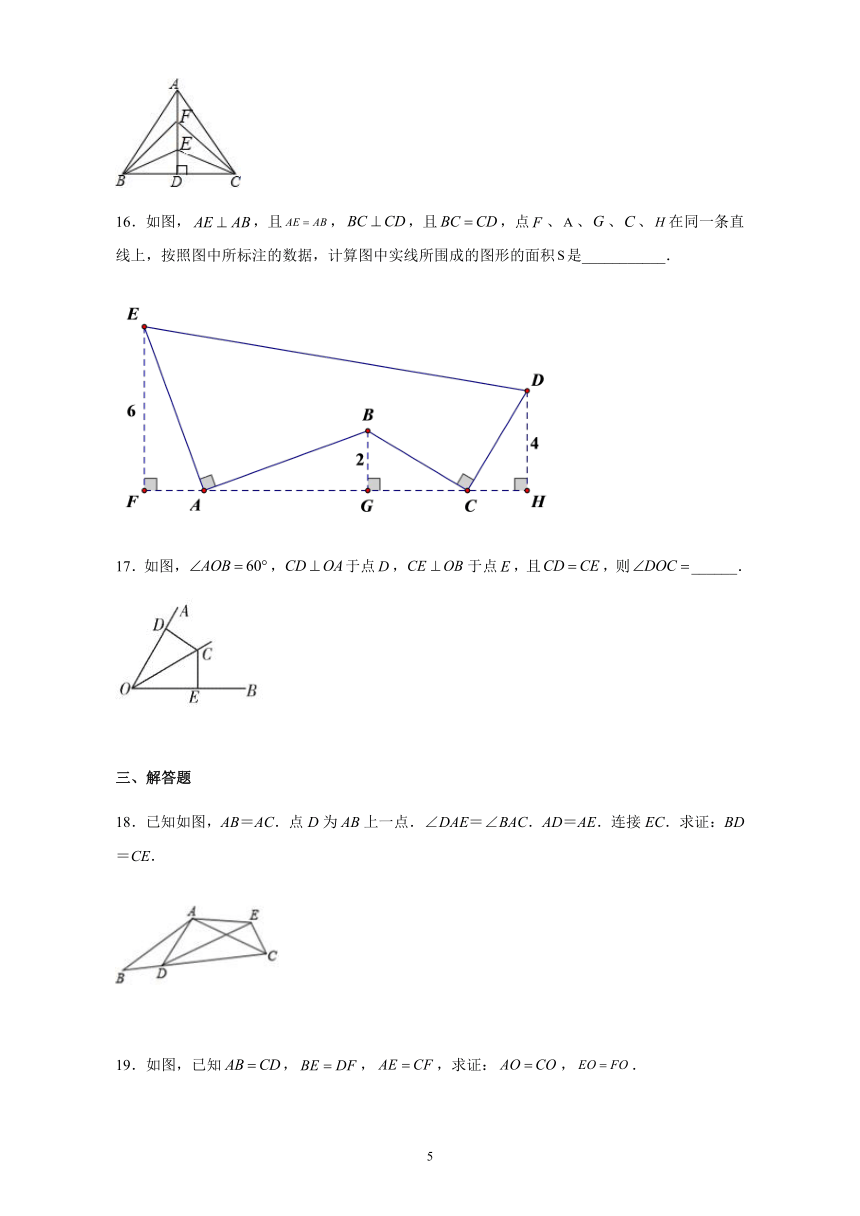
16.如图,,且,,且,点、、、、在同一条直线上,按照图中所标注的数据,计算图中实线所围成的图形的面积是___________.
17.如图,,于点,于点,且,则______.
三、解答题
18.已知如图,AB=AC.点D为AB上一点.∠DAE=∠BAC.AD=AE.连接EC.求证:BD=CE.
19.如图,已知,,,求证:,.
20.已知:如图,,,,,,垂足分别是E、F,求证:.
21.已知,线段AC、BD交于点O,,于点F,于点E,,则
(1)如图,若为钝角,求证:;
(2)若为锐角,其他条件不变,请画图判断(1)中的结论是否仍然成立?若成立,请加以证明;若不成立,请说明理由.
22.如图所示,在人教版八年级上册数学教材P53的数学活动中有这样一段描述:
(1)D为△ABC外一点,若AD=CD,AB=CB,则我们把这种两组邻边分别相等的四边形叫做“筝形”,试猜想筝形的角、对角线有什么性质?然后选择其中一条性质用全等三角形的知识证明你的猜想.
(2)知识拓展:如果D为△ABC内一点,BD平分∠ABC,且AD=CD,试证明:AB=CB.
参考答案
1.B
解:①有一个锐角和它的对边分别相等的两个直角三角形可用“AAS”判定全等,故该说法正确;
②有两边分别对应相等的两个直角三角形全等,故该说法错误;
③有两个锐角和斜边分别相等的两个直角三角形可用“ASA”判定全等,故该说法正确;
故选B.
2.D
解:第一种情况,当两个三角形全等时,是相等关系,
第二种情况,如图,,
高,
延长
与高交于,
,
在和中,
,
,
,
此时,,
是互补关系,
综上所述,这两个三角形的第三条边所对的角的关系是“相等或互补”.
故选:.
3.C
解:∵∠ACB=∠DAC,AC=CA,
∴当添加AB∥CD时,∠BAC=∠DCA,则可根据“ASA”判断△BAC≌△DCA;
当添加∠B=∠D时,则可根据“AAS”判断△BAC≌△DCA;
当添加AB=CD时,“SSA”不能判断△BAC≌△DCA.
当添加AD=BC时,则可根据“SAS”判断△BAC≌△DCA.
故选:C.
4.D
解:在△OCD和△中,
,
∴(SSS),
∴∠DOC=∠.
故选择D.
5.B
解:延长AD至M使DM=AD,连接CM,
∵是的边上的中线,
∴BD=CD,
∵∠ADB=∠CDM,
∴,
∴MC=AB=5cm,AD=DM=4cm,
在中,3<AC<13,
故选:B
6.A
解:、添加条件判定用的判定方法是,故原题说法正确,符合题意;
、添加条件不能判定,故原题说法错误,不符合题意;
、添加条件判定用的判定方法是,故原题说法错误,不符合题意;
、添加条件判定用的判定方法是,故原题说法错误,不符合题意;
故选:A.
7.B
解:当时,
,即,
解得:;
当时,
米,
此时所用时间为9秒,
米,不合题意,舍去;
综上,出发6秒后,在线段上有一点,使与全等;
故选:B.
8.C
解:∵BF⊥AB,DE⊥BF,
∴∠ABC=∠BDE
在△EDC和△ABC中,
,
∴△EDC≌△ABC(ASA).
∴ED=AB.
∵ED=30米,
∴AB=30米.
故选:C.
9.C
解:,
,
,
①当时,可根据“”判断,符合题意;
②当时,不能判断,不符合题意;
③当时,可根据“”判断,符合题意;
④当时,可根据“”判断,符合题意,
故有3个可选,
故选:C.
10.C
解:士兵的视线通过帽檐正好落在碉堡的底部点B;然后转过身保持刚才的姿势,这时视线落在了我军阵地的点E上;
得∠A=∠D,
∵AC=DF,
∴∠ACB=∠DFE=90°,
∴判定△ABC≌△DFE的理由是ASA.
故选:C.
11.B
解:∵∠B=∠D=90°,
∴△ABC和△ADC是直角三角形,
在Rt△ABC和Rt△ADC中,
,
∴Rt△ABC≌Rt△ADC(HL),
∴AB=AD,AC=AC,∠BAC=∠DAC,∠BCA=∠DCA,
即AC平分∠BAD,CA平分∠BCD,
故B说法错误,符合题意.
故选:B.
12.C
解:∵在△BFD和△CDE中,
,
∴△BFD≌△CDE(SAS),
∴∠BFD=∠CDE,
∵∠B=∠C,∠A=50°,
∴∠B=∠C=×(180°-∠A)=65°,
∴∠FDB+∠CDE=∠FDB+∠BFD=180°-∠B=115°,
∴∠FDE=180°-(∠FDB+∠EDC)=180°-115°=65°,
故选:C.
13.
解:
故答案为:
14.60°
10
解:
,,
O为BD中点,
故答案为:
15.6
解:∵AB=AC,AD⊥BC,
∴AD为BC的垂直平分线,BD=CD,∠BAD=∠CAD
∴EB=EC,FB=FC,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SAS),
同理可得△EBD≌△ECD,△ABE≌△ACE,△FBD≌△FCD,△ABF≌△ACF,△FBE≌△FCE,
∴共有6对三角形全等,
故答案为:6.
16.50
解:如题干中图所示:∵∠F=90°,
∴∠FEA+∠FAE=90°,
∵∠EAB=90°,
∴∠BAG+∠FAE=90°,
∴∠FEA=∠GAB,
在△EFA和△AGB中:,
∴△EFA≌△AGB(AAS),
∴FA=BG=2,
∴,
同理可证:△BGC≌△CHD(AAS),
∴GC=HD=4,
,
∴图中实线所围成的图形的面积=,
故答案为:50.
17.30°
解:∵、
∴
又∵
∴
∴
又∵
∴
故答案为30°
18.见解析
解:∵∠DAE=∠BAC,
∴∠DAE-∠DAC=∠BAC-∠DAC,
∴∠BAD=∠CAE
在△BAD和△CAE中
,
∴△BAD≌△CAE,
∴BD=CE.
19.证明见解析
解:
,,,
20.见解析
解:∵AC⊥BC,AD⊥BD,
∴∠ACB=∠BDA=90°,
在Rt△ACB与Rt△ABD中,
,
∴Rt△ACB≌Rt△BDA(HL),
∴∠CAB=∠DBA,AC=BD,
∵CE⊥AB,DF⊥AB,
∴=90°
在Rt△CAE与Rt△DBF中,
,
∴△CAE≌△DBF(AAS),
∴CE=DF.
21.(1)见解析;(2)成立,见解析
解:(1)∵AE=CF
∴AE+EF=EF+CF
∴AF=EC
∴在Rt△ABF和Rt△CDF中
∴Rt△ABF≌Rt△CDF(HL)
∴∠A=∠C
∴在△AOB和△DOC中
∴△AOB≌△COD(AAS)
∴BO=DO
(2)
∵AE=CF
∴AE-EF=EF-CF
∴AF=EC
∴在Rt△ABF和Rt△CDF中
∴Rt△ABF≌Rt△CDF(HL)
∴∠A=∠C
∴在△AOB和△DOC中
∴△AOB≌△COD(AAS)
∴BO=DO
22.(1)见解析;(2)见解析
解:(1)猜想BD⊥AC,∠BAD=∠BCD.
∵AD=CD,AB=CB,
在△ADB和△BCD中,
∴△ADB≌△CDB(SSS),
∴∠BAD=∠BCD,∠ADO=∠CDO,
在△AOD和△ODC中,
,
∴△AOD≌△COD(SAS),
∴∠AOD=∠COD,
而∠AOD+∠COD=180°,
∴∠DOC=90°,
∴BD⊥AC.
(2)如图,过点D分别作DE⊥AB,DF⊥ACA,垂足分别为E,F,
∵BD平分∠ABC,
∴DE=DF,
∵AD=AD,
∴Rt△BDE≌Rt△BDF(HL),
∴BE=BF,
∵ED=FD,AD=CD,
∴Rt△ADE≌Rt△CDF(HL),
∴AE=CF,
∴BE+AE=CF+BF,即AB=CB.
一、单选题
1.下列说法正确的个数有(
)
①有一个锐角和它的对边分别相等的两个直角三角形全等;②有两边分别相等的两个直角三角形全等;③有两个锐角和斜边分别相等的两个直角三角形全等.
A.3个
B.2个
C.1个
D.0个
2.如果两个三角形中两条边分别相等,且相等的一对边上的高也相等,那么这两个三角形的第三条边所对的角的关系是(
)
A.相等
B.不相等
C.互余或相等
D.互补或相等
3.如图,在四边形ABCD中,∠ACB=∠DAC,添加一个条件后不能保证△BAC≌△DCA是( )
A.AB∥CD
B.∠B=∠D
C.AB=CD
D.AD=BC
4.如图,已知,用直尺和圆规按照以下步骤作图:
①以点为圆心,任意长为半径画弧,分别交,于点,;
②画射线,以点为圆心,长为半径画弧,交于点;
③以点为圆心,长为半径画弧,与第②步中所画的弧相交于点;
④过点画射线;
根据以上操作,可以判定,其判定的依据是(
)
A.
B.
C.
D.
5.如图所示,是的边上的中线,cm,cm,则边的长度可能是(
)
A.3cm
B.5cm
C.14cm
D.13cm
6.已知:如图,,,要使,需添加一个条件,则添加的条件以及相应的判定定理合适的是(
)
A.
B.
C.
D.
7.如图,已知线段米,于点,米,射线于,点从点向运动,每秒走米,点从点向运动,每秒走米,、同时从出发,则出发秒后,在线段上有一点,使与全等,则的值为(
)
A.
B.
C.或
D.或
8.如图,要测量河两岸相对的两点A、B的距离,先在河岸BF上取两点C、D,使CD=BC,再作DE⊥BF,垂足为D,使A、C、E三点在一条直线上,测得ED=30米,因此AB的长是(
)
A.10米
B.20米
C.30米
D.40米
9.如图,已知∠1=∠2,AC=AD,要使△ABC≌△AED,还需添加一个条件,那么在①AB=AE,②BC=ED;③∠C=∠D,④∠B=∠E,这四个关系中可以选择的是( )
A.1个
B.2个
C.3个
D.4个
10.如图,抗日战争期间,为了炸毁敌人的碉堡,需要测出我军阵地与敌人碉堡的距离.我军战士想到一个办法,他先面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部点B;然后转过身保持刚才的姿势,这时视线落在了我军阵地的点E上;最后,他用步测的办法量出自己与E点的距离,从而推算出我军阵地与敌人碉堡的距离,这里判定△ABC≌△DFE的理由可以是( )
A.SSS
B.SAS
C.ASA
D.AAA
11.如图,在和中,,,则下列说法错误的是(
)
A.
B.
C.平分
D.平分
12.如图,在中,,则的度数为(
)
A.
B.
C.
D.
二、填空题
13.如图,,,,AC、BD相交于E,则的度数为____________.
14.如图,,,O为BD中点,过O点作直线与DA、BC延长线交于E,F,若,,则_________,_________.
15.如图,,于D点,E、F为AD上的点,则图中共有____对全等三角形.
16.如图,,且,,且,点、、、、在同一条直线上,按照图中所标注的数据,计算图中实线所围成的图形的面积是___________.
17.如图,,于点,于点,且,则______.
三、解答题
18.已知如图,AB=AC.点D为AB上一点.∠DAE=∠BAC.AD=AE.连接EC.求证:BD=CE.
19.如图,已知,,,求证:,.
20.已知:如图,,,,,,垂足分别是E、F,求证:.
21.已知,线段AC、BD交于点O,,于点F,于点E,,则
(1)如图,若为钝角,求证:;
(2)若为锐角,其他条件不变,请画图判断(1)中的结论是否仍然成立?若成立,请加以证明;若不成立,请说明理由.
22.如图所示,在人教版八年级上册数学教材P53的数学活动中有这样一段描述:
(1)D为△ABC外一点,若AD=CD,AB=CB,则我们把这种两组邻边分别相等的四边形叫做“筝形”,试猜想筝形的角、对角线有什么性质?然后选择其中一条性质用全等三角形的知识证明你的猜想.
(2)知识拓展:如果D为△ABC内一点,BD平分∠ABC,且AD=CD,试证明:AB=CB.
参考答案
1.B
解:①有一个锐角和它的对边分别相等的两个直角三角形可用“AAS”判定全等,故该说法正确;
②有两边分别对应相等的两个直角三角形全等,故该说法错误;
③有两个锐角和斜边分别相等的两个直角三角形可用“ASA”判定全等,故该说法正确;
故选B.
2.D
解:第一种情况,当两个三角形全等时,是相等关系,
第二种情况,如图,,
高,
延长
与高交于,
,
在和中,
,
,
,
此时,,
是互补关系,
综上所述,这两个三角形的第三条边所对的角的关系是“相等或互补”.
故选:.
3.C
解:∵∠ACB=∠DAC,AC=CA,
∴当添加AB∥CD时,∠BAC=∠DCA,则可根据“ASA”判断△BAC≌△DCA;
当添加∠B=∠D时,则可根据“AAS”判断△BAC≌△DCA;
当添加AB=CD时,“SSA”不能判断△BAC≌△DCA.
当添加AD=BC时,则可根据“SAS”判断△BAC≌△DCA.
故选:C.
4.D
解:在△OCD和△中,
,
∴(SSS),
∴∠DOC=∠.
故选择D.
5.B
解:延长AD至M使DM=AD,连接CM,
∵是的边上的中线,
∴BD=CD,
∵∠ADB=∠CDM,
∴,
∴MC=AB=5cm,AD=DM=4cm,
在中,3<AC<13,
故选:B
6.A
解:、添加条件判定用的判定方法是,故原题说法正确,符合题意;
、添加条件不能判定,故原题说法错误,不符合题意;
、添加条件判定用的判定方法是,故原题说法错误,不符合题意;
、添加条件判定用的判定方法是,故原题说法错误,不符合题意;
故选:A.
7.B
解:当时,
,即,
解得:;
当时,
米,
此时所用时间为9秒,
米,不合题意,舍去;
综上,出发6秒后,在线段上有一点,使与全等;
故选:B.
8.C
解:∵BF⊥AB,DE⊥BF,
∴∠ABC=∠BDE
在△EDC和△ABC中,
,
∴△EDC≌△ABC(ASA).
∴ED=AB.
∵ED=30米,
∴AB=30米.
故选:C.
9.C
解:,
,
,
①当时,可根据“”判断,符合题意;
②当时,不能判断,不符合题意;
③当时,可根据“”判断,符合题意;
④当时,可根据“”判断,符合题意,
故有3个可选,
故选:C.
10.C
解:士兵的视线通过帽檐正好落在碉堡的底部点B;然后转过身保持刚才的姿势,这时视线落在了我军阵地的点E上;
得∠A=∠D,
∵AC=DF,
∴∠ACB=∠DFE=90°,
∴判定△ABC≌△DFE的理由是ASA.
故选:C.
11.B
解:∵∠B=∠D=90°,
∴△ABC和△ADC是直角三角形,
在Rt△ABC和Rt△ADC中,
,
∴Rt△ABC≌Rt△ADC(HL),
∴AB=AD,AC=AC,∠BAC=∠DAC,∠BCA=∠DCA,
即AC平分∠BAD,CA平分∠BCD,
故B说法错误,符合题意.
故选:B.
12.C
解:∵在△BFD和△CDE中,
,
∴△BFD≌△CDE(SAS),
∴∠BFD=∠CDE,
∵∠B=∠C,∠A=50°,
∴∠B=∠C=×(180°-∠A)=65°,
∴∠FDB+∠CDE=∠FDB+∠BFD=180°-∠B=115°,
∴∠FDE=180°-(∠FDB+∠EDC)=180°-115°=65°,
故选:C.
13.
解:
故答案为:
14.60°
10
解:
,,
O为BD中点,
故答案为:
15.6
解:∵AB=AC,AD⊥BC,
∴AD为BC的垂直平分线,BD=CD,∠BAD=∠CAD
∴EB=EC,FB=FC,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SAS),
同理可得△EBD≌△ECD,△ABE≌△ACE,△FBD≌△FCD,△ABF≌△ACF,△FBE≌△FCE,
∴共有6对三角形全等,
故答案为:6.
16.50
解:如题干中图所示:∵∠F=90°,
∴∠FEA+∠FAE=90°,
∵∠EAB=90°,
∴∠BAG+∠FAE=90°,
∴∠FEA=∠GAB,
在△EFA和△AGB中:,
∴△EFA≌△AGB(AAS),
∴FA=BG=2,
∴,
同理可证:△BGC≌△CHD(AAS),
∴GC=HD=4,
,
∴图中实线所围成的图形的面积=,
故答案为:50.
17.30°
解:∵、
∴
又∵
∴
∴
又∵
∴
故答案为30°
18.见解析
解:∵∠DAE=∠BAC,
∴∠DAE-∠DAC=∠BAC-∠DAC,
∴∠BAD=∠CAE
在△BAD和△CAE中
,
∴△BAD≌△CAE,
∴BD=CE.
19.证明见解析
解:
,,,
20.见解析
解:∵AC⊥BC,AD⊥BD,
∴∠ACB=∠BDA=90°,
在Rt△ACB与Rt△ABD中,
,
∴Rt△ACB≌Rt△BDA(HL),
∴∠CAB=∠DBA,AC=BD,
∵CE⊥AB,DF⊥AB,
∴=90°
在Rt△CAE与Rt△DBF中,
,
∴△CAE≌△DBF(AAS),
∴CE=DF.
21.(1)见解析;(2)成立,见解析
解:(1)∵AE=CF
∴AE+EF=EF+CF
∴AF=EC
∴在Rt△ABF和Rt△CDF中
∴Rt△ABF≌Rt△CDF(HL)
∴∠A=∠C
∴在△AOB和△DOC中
∴△AOB≌△COD(AAS)
∴BO=DO
(2)
∵AE=CF
∴AE-EF=EF-CF
∴AF=EC
∴在Rt△ABF和Rt△CDF中
∴Rt△ABF≌Rt△CDF(HL)
∴∠A=∠C
∴在△AOB和△DOC中
∴△AOB≌△COD(AAS)
∴BO=DO
22.(1)见解析;(2)见解析
解:(1)猜想BD⊥AC,∠BAD=∠BCD.
∵AD=CD,AB=CB,
在△ADB和△BCD中,
∴△ADB≌△CDB(SSS),
∴∠BAD=∠BCD,∠ADO=∠CDO,
在△AOD和△ODC中,
,
∴△AOD≌△COD(SAS),
∴∠AOD=∠COD,
而∠AOD+∠COD=180°,
∴∠DOC=90°,
∴BD⊥AC.
(2)如图,过点D分别作DE⊥AB,DF⊥ACA,垂足分别为E,F,
∵BD平分∠ABC,
∴DE=DF,
∵AD=AD,
∴Rt△BDE≌Rt△BDF(HL),
∴BE=BF,
∵ED=FD,AD=CD,
∴Rt△ADE≌Rt△CDF(HL),
∴AE=CF,
∴BE+AE=CF+BF,即AB=CB.
