2021-2022学年北师大版八年级数学上册1.3 勾股定理的应用 同步训练(word版、含解析)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册1.3 勾股定理的应用 同步训练(word版、含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 343.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
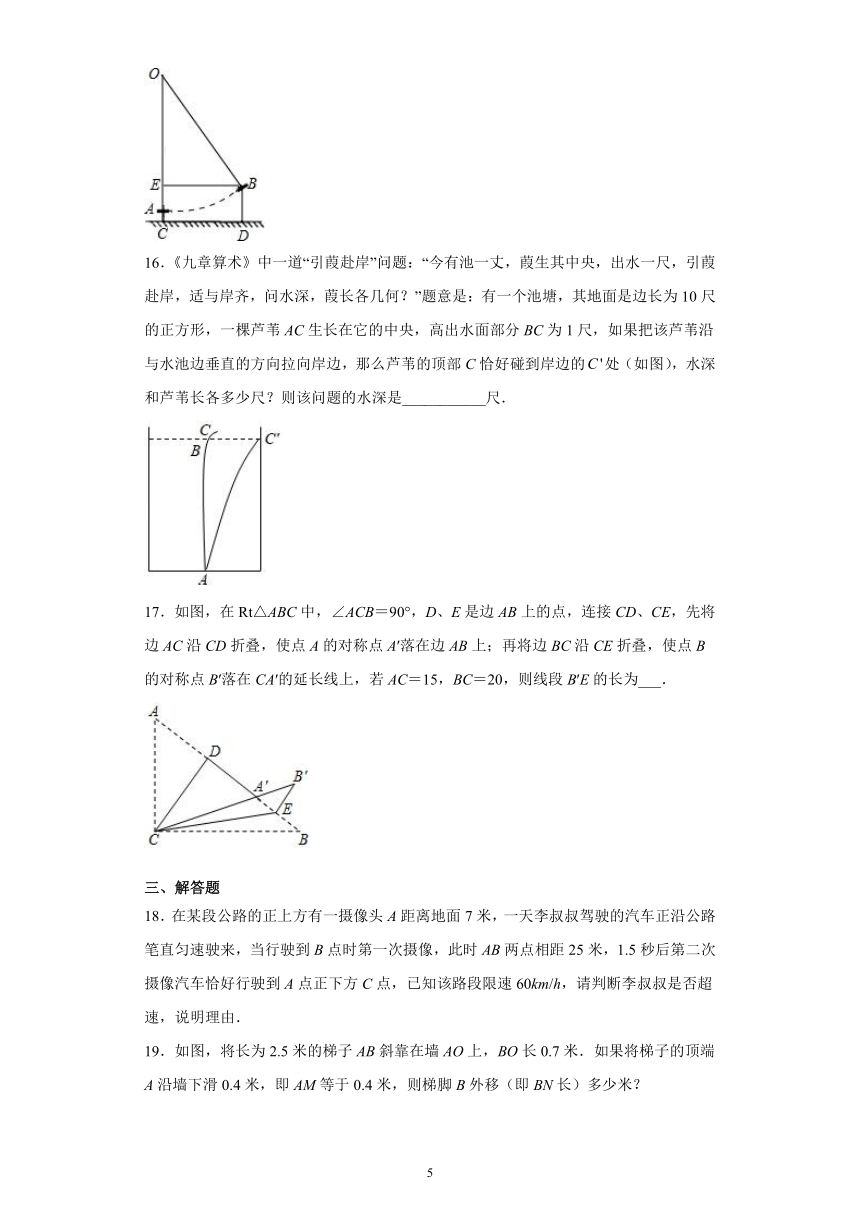
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 09:47:33 | ||
图片预览

文档简介
第一章3
勾股定理的应用
一、单选题
1.我国古代数学名著《九章算术》中有这样一道题目“勾股定理的应用今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽.问索长几何?”译文为“今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵索沿地面退行,在离木柱根部8尺处时,绳索用尽.问绳索长是多少?”示意图如图所示,设绳索AC的长为x尺,根据题意,可列方程为(
)
A.x2﹣(x+3)2=82
B.x2﹣(x﹣3)2=82
C.(x+3)2﹣x2=82
D.x2﹣(x﹣3)2=8
2.如图,一个梯子斜靠在一竖直的墙AO上,测得AO=4m,若梯子的顶端沿墙下滑1m,这时梯子的底端也下滑1m,则梯子AB的长度为( )
A.5m
B.6m
C.3m
D.7m
3.如图,有一个圆柱,底面圆的直径AB=cm,高BC=12cm,P为BC的中点,一只蚂蚁从A点出发沿着圆柱的表面爬到P点的最短距离为( )
A.9cm
B.10cm
C.11cm
D.12cm
4.如图,正四棱柱的底面边长为10cm,侧棱长为16cm,一只蚂蚁从点A出发,沿棱柱侧面到点C′处吃食物,那么它需要爬行的最短路径的长是( )cm
A.8
B.4
C.2
D.12
5.一根竹子高一丈,折断后竹子顶端落在离竹子底端6尺处,折断处离地面的高度是多少?(这是我国古代《九章算术》中的“折竹抵地问题.其中的丈、尺是长度单位,一丈=10尺)设折断处离地面的高度为x尺,则可列方程为(
)
A.x2+62=(10﹣x)2
B.x2﹣62=(10﹣x)2
C.x2+6=(10﹣x)2
D.x2﹣6=(10﹣x)2
6.如图,在一次测绘活动中,某同学站在点A的位置观测停放于B,C两处的小船,测得船B在点A北偏东75°方向900米处,船C在点A南偏东15°方向1200米处,则船B与船C之间的距离为(
)
A.1500m
B.1200m
C.1000m
D.800m
7.如图,要从电线杆离地面处向地面拉一条长为的钢缆.则地面钢缆固定点A到电线杆底部点B的距离是(
)
A.
B.
C.
D.
8.如图,是一段楼梯,高BC是1.5m,斜边AC是2.5m,如果在楼梯上铺地毯,那么至少需要地毯( )
A.2.5m
B.3m
C.3.5m
D.4m
9.《九章算术》是我国古代数学的经典著作,书中有一个“折竹抵地”问题:“今有竹高丈,末折抵地,问折者高几何?“意思是:一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,问:原处还有多高的竹子?(
)
A.4尺
B.4.55尺
C.5.45尺
D.5.55尺
10.某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图).在三棱镜的侧面上,从顶点A到顶点A′镶有一圈金属丝,已知此三棱镜的高为9cm,底面边长为4cm,则这圈金属丝的长度至少为( )
A.8cm
B.10cm
C.12cm
D.15cm
11.如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池边,它的顶端恰好到达池边的水面,求水的深度是( )尺
A.8
B.10
C.13
D.12
12.如图,八年级一班的同学准备测量校园人工湖的深度,他们把一根竹竿竖直插到水底,此时竹竿离岸边点C处的距离米.竹竿高出水面的部分长0.2米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则人工湖的深度为( )
A.1.5米
B.1.7米
C.1.8米
D.0.6米
二、填空题
13.如图,一艘轮船以8海里/时的速度从港口O出发向东北方向航行,另一轮船以6海里/时O出发向东南方向航行,离开港口0.5小时后,两船相距_________海里.
14.如图,一木杆在离地面9米处断裂,木杆顶部落在离木杆底端12米处,则木杆折断之前高_______米.
15.明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千OA静止的时候,踏板离地高一尺(尺),将它往前推进两步(尺),此时踏板升高离地五尺(尺),则秋千绳索(OA或OB)的长度为______尺.
16.《九章算术》中一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AC生长在它的中央,高出水面部分BC为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部C恰好碰到岸边的处(如图),水深和芦苇长各多少尺?则该问题的水深是___________尺.
17.如图,在Rt△ABC中,∠ACB=90°,D、E是边AB上的点,连接CD、CE,先将边AC沿CD折叠,使点A的对称点A′落在边AB上;再将边BC沿CE折叠,使点B的对称点B′落在CA′的延长线上,若AC=15,BC=20,则线段B′E的长为___.
三、解答题
18.在某段公路的正上方有一摄像头A距离地面7米,一天李叔叔驾驶的汽车正沿公路笔直匀速驶来,当行驶到B点时第一次摄像,此时AB两点相距25米,1.5秒后第二次摄像汽车恰好行驶到A点正下方C点,已知该路段限速60km/h,请判断李叔叔是否超速,说明理由.
19.如图,将长为2.5米的梯子AB斜靠在墙AO上,BO长0.7米.如果将梯子的顶端A沿墙下滑0.4米,即AM等于0.4米,则梯脚B外移(即BN长)多少米?
20.已知等腰三角形腰长是10,底边长是16,求这个等腰三角形的面积.
21.如图,,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,隧道总长为2公里,已知高速公路一公里造价为300万元,隧道一公里造价为500万元,公里,公里,则改建后可省工程费用多少万元?
22.如图,A、B两点相距14km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=8km,CB=6km,现在要在AB上建一个供水站E,使得C、D两村到供水站E站的距离相等,则:
(1)站应建在距站多少千米处?
(2)和垂直吗?说明理由.
参考答案
1.B
解:设绳索的长为尺,则木柱的长为尺,
在中,
由勾股定理得,,
∴,
故选:B.
2.A
解:设BO=xm,
由题意得:AC=1m,BD=1m,AO=4m,
在Rt△AOB中,根据勾股定理得:AB2=AO2+OB2=42+x2,
在Rt△COD中,根据勾股定理得:CD2=CO2+OD2=(4﹣1)2+(x+1)2,
∴42+x2=(4﹣1)2+(x+1)2,
解得:x=3,
,
即梯子AB的长为5m,
故选:A.
3.B
解:已知如图:
∵圆柱底面直径AB=cm、母线BC=12cm,P为BC的中点,
∴圆柱底面圆的半径是cm,BP=6cm,
∴AB=×2××π=8cm,
在Rt△ABP中,(cm),
∴蚂蚁从A点爬到P点的最短距离为10cm,
故选:B.
4.B
解:把正四棱柱展开为平面图形,分两种情形:
如图1中,,
如图2中,,
∵
,
∴爬行的最短路径是cm.
故选B
5.A
解:1丈=10尺,
设折断处离地面的高度为x尺,则斜边为(10-x)尺,
根据勾股定理得:x2+62=(10-x)2,
故选:A.
6.A
解:由题意可知∠NAB=75°,∠SAC=15°,
∴∠BAC=90°,
∵AB=900米,AC=1200米,
∴BC==1500米.
故选A.
7.D
解:如图:
地面钢缆固定点到电杆底部的距离为
.
故选:D.
8.C
解:由勾股定理得:
AB=,
因为地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,
所以地毯的长度至少是1.5+2=3.5(m).
故选C.
9.B
解:设竹子折断处离地面x尺,则斜边为(10 x)尺,
根据勾股定理得:x2+32=(10 x)2,
解得:x=4.55.
故选B.
10.D
解:将三棱柱沿展开,其展开图如图,
则.
故选:.
11.D
解:设芦苇的长为x尺,即BC=x尺,则AB=(x-1)尺,AC=5尺
由题意可得:
∴
解得
∴尺
故选D.
12.A
解:设BD的长度为xm,则AB=BC=(x+0.2)m,
在Rt△CDB中,0.82+x2=(x+0.2)2,
解得x=1.5.
故选:A.
13.5
解:∵两船行驶的方向是东北方向和东南方向,
∴∠BAC=90°,
0.5小时后,两艘船分别行驶了:8×0.5=4(海里),6×0.5=3(海里).
则两船相距:5(海里).
故答案为:5.
14.24
解:作图如下,
∵一棵垂直于地面的大树在离地面9米处折断,树的顶端落在离树杆底部12米处,
∴折断的部分长为
15,
∴折断前高度为15+9=24(米).
故答案为:24.
15.14.5
解:设OA=OB=x尺,
∵EC=BD=5尺,AC=1尺,
∴EA=EC-AC=5-1=4(尺),
OE=OA-AE=(x-4)尺,
在Rt△OEB中,OE=(x-4)尺,OB=x尺,EB=10尺,
根据勾股定理得:x2=(x-4)2+102,
整理得:8x=116,
即2x=29,
解得:x=14.5,
答:秋千绳索的长度是14.5尺.
故答案为:14.5.
16.12
解:依题意画出图形,
设芦苇长尺,
则水深尺,
∵尺,
∴尺,
在中,
,
解得,
即芦苇长13尺,水深为12尺,
故答案为:12.
17.4
根据折叠的性质可知:
,,CD⊥AB,
,,,
∵,
∵,
∴,
∴是等腰直角三角形,
∴,
∴,
∵根据勾股定理得:
,
∴,
∴,
∴,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
故答案为:4.
18.李叔叔不超速,理由见解析
解:李叔叔不超速,理由如下:
如图,
Rt△ABC中,AC=7,AB=25,
由勾股定理得:BC==24,
v=24÷1.5=16(m/s)=57.6(km/h),
∵57.6<60,
∴李叔叔不超速.
19.梯脚外移0.8米.
解:由题意得:AB=2.5米,BO=0.7米,
在Rt△ABO中,由勾股定理得:
(米).
∴MO=AO-AM=2.4-0.4=2(米),
在Rt△MNO中,由勾股定理得:
(米).
∴NB=ON-OB=1.5-0.7=0.8(米),
∴梯脚B外移(即BN长)0.8米.
20.48
如图,△ABC中,AB=
AC=
10,BC=
16,过点A作AD⊥BC于D,
∴BD=CD=BC=×16=8
∴∠ADB=90°
.∴
AD===6
∴S
=BC×AD=×16×6=48
∴这个等腰三角形的面积是48
21.11600
解:根据勾股定理得:
原计划建公路费用:万元,
实际打隧道及建公路费用:万元,
万元,
答:改建后可省工程费11600万元.
22.(1)E站应建在距A站6千米处;(2)DE和EC垂直,理由见解析
解:(1)∵使得C,D两村到E站的距离相等.
∴DE=CE,
∵DA⊥AB于A,CB⊥AB于B,
∴∠A=∠B=90°,
∴AE2+AD2=DE2,BE2+BC2=EC2,
∴AE2+AD2=BE2+BC2,
设AE=x,则BE=AB-AE=(14-x),
∵DA=8km,CB=6km,
∴x2+82=(14-x)2+62,
解得:x=6,
∴AE=6km.
答:E站应建在距A站6千米处;
(2)DE和EC垂直,理由如下:
在△DAE与△EBC中,
,
∴△DAE≌△EBC(SAS),
∴∠DEA=∠ECB,∠D=∠CEB,
∵∠DEA+∠D=90°,
∴∠DEA+∠CEB=90°,
∴∠DEC=90°,
即DE⊥EC.
勾股定理的应用
一、单选题
1.我国古代数学名著《九章算术》中有这样一道题目“勾股定理的应用今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽.问索长几何?”译文为“今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵索沿地面退行,在离木柱根部8尺处时,绳索用尽.问绳索长是多少?”示意图如图所示,设绳索AC的长为x尺,根据题意,可列方程为(
)
A.x2﹣(x+3)2=82
B.x2﹣(x﹣3)2=82
C.(x+3)2﹣x2=82
D.x2﹣(x﹣3)2=8
2.如图,一个梯子斜靠在一竖直的墙AO上,测得AO=4m,若梯子的顶端沿墙下滑1m,这时梯子的底端也下滑1m,则梯子AB的长度为( )
A.5m
B.6m
C.3m
D.7m
3.如图,有一个圆柱,底面圆的直径AB=cm,高BC=12cm,P为BC的中点,一只蚂蚁从A点出发沿着圆柱的表面爬到P点的最短距离为( )
A.9cm
B.10cm
C.11cm
D.12cm
4.如图,正四棱柱的底面边长为10cm,侧棱长为16cm,一只蚂蚁从点A出发,沿棱柱侧面到点C′处吃食物,那么它需要爬行的最短路径的长是( )cm
A.8
B.4
C.2
D.12
5.一根竹子高一丈,折断后竹子顶端落在离竹子底端6尺处,折断处离地面的高度是多少?(这是我国古代《九章算术》中的“折竹抵地问题.其中的丈、尺是长度单位,一丈=10尺)设折断处离地面的高度为x尺,则可列方程为(
)
A.x2+62=(10﹣x)2
B.x2﹣62=(10﹣x)2
C.x2+6=(10﹣x)2
D.x2﹣6=(10﹣x)2
6.如图,在一次测绘活动中,某同学站在点A的位置观测停放于B,C两处的小船,测得船B在点A北偏东75°方向900米处,船C在点A南偏东15°方向1200米处,则船B与船C之间的距离为(
)
A.1500m
B.1200m
C.1000m
D.800m
7.如图,要从电线杆离地面处向地面拉一条长为的钢缆.则地面钢缆固定点A到电线杆底部点B的距离是(
)
A.
B.
C.
D.
8.如图,是一段楼梯,高BC是1.5m,斜边AC是2.5m,如果在楼梯上铺地毯,那么至少需要地毯( )
A.2.5m
B.3m
C.3.5m
D.4m
9.《九章算术》是我国古代数学的经典著作,书中有一个“折竹抵地”问题:“今有竹高丈,末折抵地,问折者高几何?“意思是:一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,问:原处还有多高的竹子?(
)
A.4尺
B.4.55尺
C.5.45尺
D.5.55尺
10.某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图).在三棱镜的侧面上,从顶点A到顶点A′镶有一圈金属丝,已知此三棱镜的高为9cm,底面边长为4cm,则这圈金属丝的长度至少为( )
A.8cm
B.10cm
C.12cm
D.15cm
11.如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池边,它的顶端恰好到达池边的水面,求水的深度是( )尺
A.8
B.10
C.13
D.12
12.如图,八年级一班的同学准备测量校园人工湖的深度,他们把一根竹竿竖直插到水底,此时竹竿离岸边点C处的距离米.竹竿高出水面的部分长0.2米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则人工湖的深度为( )
A.1.5米
B.1.7米
C.1.8米
D.0.6米
二、填空题
13.如图,一艘轮船以8海里/时的速度从港口O出发向东北方向航行,另一轮船以6海里/时O出发向东南方向航行,离开港口0.5小时后,两船相距_________海里.
14.如图,一木杆在离地面9米处断裂,木杆顶部落在离木杆底端12米处,则木杆折断之前高_______米.
15.明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千OA静止的时候,踏板离地高一尺(尺),将它往前推进两步(尺),此时踏板升高离地五尺(尺),则秋千绳索(OA或OB)的长度为______尺.
16.《九章算术》中一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AC生长在它的中央,高出水面部分BC为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部C恰好碰到岸边的处(如图),水深和芦苇长各多少尺?则该问题的水深是___________尺.
17.如图,在Rt△ABC中,∠ACB=90°,D、E是边AB上的点,连接CD、CE,先将边AC沿CD折叠,使点A的对称点A′落在边AB上;再将边BC沿CE折叠,使点B的对称点B′落在CA′的延长线上,若AC=15,BC=20,则线段B′E的长为___.
三、解答题
18.在某段公路的正上方有一摄像头A距离地面7米,一天李叔叔驾驶的汽车正沿公路笔直匀速驶来,当行驶到B点时第一次摄像,此时AB两点相距25米,1.5秒后第二次摄像汽车恰好行驶到A点正下方C点,已知该路段限速60km/h,请判断李叔叔是否超速,说明理由.
19.如图,将长为2.5米的梯子AB斜靠在墙AO上,BO长0.7米.如果将梯子的顶端A沿墙下滑0.4米,即AM等于0.4米,则梯脚B外移(即BN长)多少米?
20.已知等腰三角形腰长是10,底边长是16,求这个等腰三角形的面积.
21.如图,,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,隧道总长为2公里,已知高速公路一公里造价为300万元,隧道一公里造价为500万元,公里,公里,则改建后可省工程费用多少万元?
22.如图,A、B两点相距14km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=8km,CB=6km,现在要在AB上建一个供水站E,使得C、D两村到供水站E站的距离相等,则:
(1)站应建在距站多少千米处?
(2)和垂直吗?说明理由.
参考答案
1.B
解:设绳索的长为尺,则木柱的长为尺,
在中,
由勾股定理得,,
∴,
故选:B.
2.A
解:设BO=xm,
由题意得:AC=1m,BD=1m,AO=4m,
在Rt△AOB中,根据勾股定理得:AB2=AO2+OB2=42+x2,
在Rt△COD中,根据勾股定理得:CD2=CO2+OD2=(4﹣1)2+(x+1)2,
∴42+x2=(4﹣1)2+(x+1)2,
解得:x=3,
,
即梯子AB的长为5m,
故选:A.
3.B
解:已知如图:
∵圆柱底面直径AB=cm、母线BC=12cm,P为BC的中点,
∴圆柱底面圆的半径是cm,BP=6cm,
∴AB=×2××π=8cm,
在Rt△ABP中,(cm),
∴蚂蚁从A点爬到P点的最短距离为10cm,
故选:B.
4.B
解:把正四棱柱展开为平面图形,分两种情形:
如图1中,,
如图2中,,
∵
,
∴爬行的最短路径是cm.
故选B
5.A
解:1丈=10尺,
设折断处离地面的高度为x尺,则斜边为(10-x)尺,
根据勾股定理得:x2+62=(10-x)2,
故选:A.
6.A
解:由题意可知∠NAB=75°,∠SAC=15°,
∴∠BAC=90°,
∵AB=900米,AC=1200米,
∴BC==1500米.
故选A.
7.D
解:如图:
地面钢缆固定点到电杆底部的距离为
.
故选:D.
8.C
解:由勾股定理得:
AB=,
因为地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,
所以地毯的长度至少是1.5+2=3.5(m).
故选C.
9.B
解:设竹子折断处离地面x尺,则斜边为(10 x)尺,
根据勾股定理得:x2+32=(10 x)2,
解得:x=4.55.
故选B.
10.D
解:将三棱柱沿展开,其展开图如图,
则.
故选:.
11.D
解:设芦苇的长为x尺,即BC=x尺,则AB=(x-1)尺,AC=5尺
由题意可得:
∴
解得
∴尺
故选D.
12.A
解:设BD的长度为xm,则AB=BC=(x+0.2)m,
在Rt△CDB中,0.82+x2=(x+0.2)2,
解得x=1.5.
故选:A.
13.5
解:∵两船行驶的方向是东北方向和东南方向,
∴∠BAC=90°,
0.5小时后,两艘船分别行驶了:8×0.5=4(海里),6×0.5=3(海里).
则两船相距:5(海里).
故答案为:5.
14.24
解:作图如下,
∵一棵垂直于地面的大树在离地面9米处折断,树的顶端落在离树杆底部12米处,
∴折断的部分长为
15,
∴折断前高度为15+9=24(米).
故答案为:24.
15.14.5
解:设OA=OB=x尺,
∵EC=BD=5尺,AC=1尺,
∴EA=EC-AC=5-1=4(尺),
OE=OA-AE=(x-4)尺,
在Rt△OEB中,OE=(x-4)尺,OB=x尺,EB=10尺,
根据勾股定理得:x2=(x-4)2+102,
整理得:8x=116,
即2x=29,
解得:x=14.5,
答:秋千绳索的长度是14.5尺.
故答案为:14.5.
16.12
解:依题意画出图形,
设芦苇长尺,
则水深尺,
∵尺,
∴尺,
在中,
,
解得,
即芦苇长13尺,水深为12尺,
故答案为:12.
17.4
根据折叠的性质可知:
,,CD⊥AB,
,,,
∵,
∵,
∴,
∴是等腰直角三角形,
∴,
∴,
∵根据勾股定理得:
,
∴,
∴,
∴,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
故答案为:4.
18.李叔叔不超速,理由见解析
解:李叔叔不超速,理由如下:
如图,
Rt△ABC中,AC=7,AB=25,
由勾股定理得:BC==24,
v=24÷1.5=16(m/s)=57.6(km/h),
∵57.6<60,
∴李叔叔不超速.
19.梯脚外移0.8米.
解:由题意得:AB=2.5米,BO=0.7米,
在Rt△ABO中,由勾股定理得:
(米).
∴MO=AO-AM=2.4-0.4=2(米),
在Rt△MNO中,由勾股定理得:
(米).
∴NB=ON-OB=1.5-0.7=0.8(米),
∴梯脚B外移(即BN长)0.8米.
20.48
如图,△ABC中,AB=
AC=
10,BC=
16,过点A作AD⊥BC于D,
∴BD=CD=BC=×16=8
∴∠ADB=90°
.∴
AD===6
∴S
=BC×AD=×16×6=48
∴这个等腰三角形的面积是48
21.11600
解:根据勾股定理得:
原计划建公路费用:万元,
实际打隧道及建公路费用:万元,
万元,
答:改建后可省工程费11600万元.
22.(1)E站应建在距A站6千米处;(2)DE和EC垂直,理由见解析
解:(1)∵使得C,D两村到E站的距离相等.
∴DE=CE,
∵DA⊥AB于A,CB⊥AB于B,
∴∠A=∠B=90°,
∴AE2+AD2=DE2,BE2+BC2=EC2,
∴AE2+AD2=BE2+BC2,
设AE=x,则BE=AB-AE=(14-x),
∵DA=8km,CB=6km,
∴x2+82=(14-x)2+62,
解得:x=6,
∴AE=6km.
答:E站应建在距A站6千米处;
(2)DE和EC垂直,理由如下:
在△DAE与△EBC中,
,
∴△DAE≌△EBC(SAS),
∴∠DEA=∠ECB,∠D=∠CEB,
∵∠DEA+∠D=90°,
∴∠DEA+∠CEB=90°,
∴∠DEC=90°,
即DE⊥EC.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
