第一章 勾股定理 单元检测卷 2021-2022学年北师大版数学八年级上册 (word版含答案)
文档属性
| 名称 | 第一章 勾股定理 单元检测卷 2021-2022学年北师大版数学八年级上册 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 179.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 10:17:39 | ||
图片预览




文档简介
北师版数学八年级上册《第一章
勾股定理》单元检测卷
一、单选题
1.在西方,人们称为毕达哥拉斯定理,在我国把它称为勾股定理,其具体内容指的是(
)
A.如果直角三角形的两条直角边分别为a,b,斜边为c,那么a2+b2=c2
B.如果直角三角形的三边分别为a,b,c,那么a2+b2=c2
C.如果三角形的三边分别为a,b,c,那么a2+b2=c2
D.如果三角形的三边长a,b,c满足a2+b2=c2
,
那么这个三角形是直角三角形
2.一直角三角形两
直角边长分别为5和12,则斜边长为(
)
A.5
B.12
C.13
D.17
3.如图是我校的长方形水泥操场,如果一学生要从A角走到C角,至少走(
)
A.140米
B.120米
C.100米
D.90米
4.如图,由两个直角三角形和三个正方形组成的图形,大直角三角形的斜边和直角边长分别是13,12.则图中阴影部分的面积是(
)
A.16
B.25
C.144
D.169
5..一帆船先向正西航行24千米,然后向正南航行10千米,这时它离出发点有(
)千米.
A. 26 B. 18 C. 13 D. 32
6.下列四组数据不能作为直角三角形的三边长的是(
)
A. 9,12,15 B. 7,24,25 C. 15,36,39 D. 12,15,20
7.已知四个三角形分别满足下列条件:①一个内角等于另两个内角之和;②三个内角度数之比为3∶4∶5;③三边长分别为7,24,25;④三边长之比为5∶12∶13.其中直角三角形有(
)
A.1个
B.2个
C.3个
D.4个
8..在
中,若
,则(
)
A. B. C. D. 不能确定
9.《九章算术》是我国古代第一部数学专著,它的出现标志着中国古代数学形成了完整的体系.“折竹抵地”问题源自《九章算术》中:今有竹高一丈,末折抵地,去根六尺,问折高者几何?意思是一根竹子,原高一丈(一丈=10尺)一阵风将竹子折断,某竹梢恰好抵地,抵地处离竹子底部6尺远,则折断处离地面的高度是(
)
A.5.3尺
B.6.8尺
C.4.7尺
D.3.2尺
10.如图,“今有竹高两丈五尺,末折抵地,去本五尺,问折者高几何?”意思是:一根竹子,原来高两丈五尺(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部五尺远,则折断处离地面的高度为(
)
A.5尺
B.25尺
C.13尺
D.12尺
11.如图,在高为
,坡面长为
的楼梯表面铺地毯,地毯的长度至少需要(
)
A.
B.
C.
D.
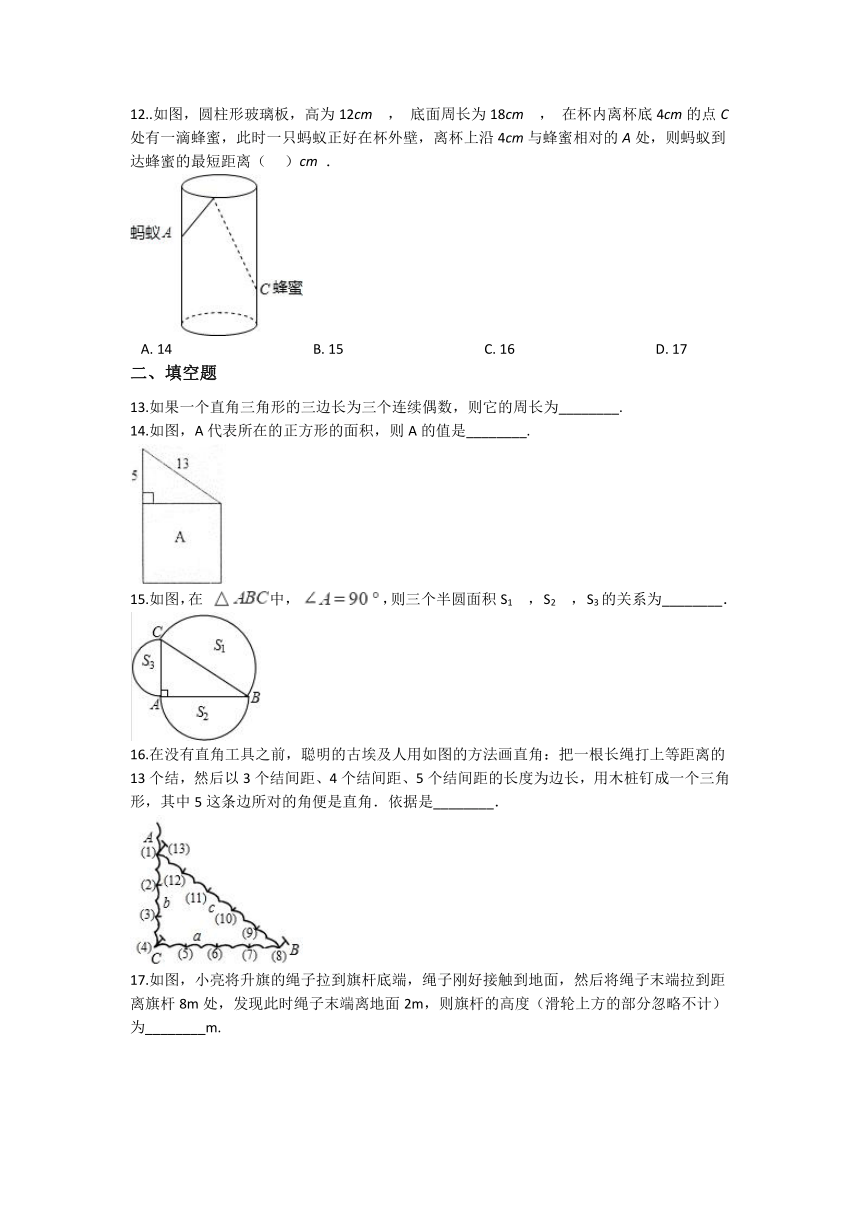
12..如图,圆柱形玻璃板,高为12cm
,
底面周长为18cm
,
在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的A处,则蚂蚁到达蜂蜜的最短距离(
)cm
.
A. 14 B. 15 C. 16 D. 17
二、填空题
13.如果一个直角三角形的三边长为三个连续偶数,则它的周长为________.
14.如图,A代表所在的正方形的面积,则A的值是________.
15.如图,在
中,
,则三个半圆面积S1
,
S2
,
S3的关系为________.
16.在没有直角工具之前,聪明的古埃及人用如图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中5这条边所对的角便是直角.依据是________.
17.如图,小亮将升旗的绳子拉到旗杆底端,绳子刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端离地面2m,则旗杆的高度(滑轮上方的部分忽略不计)为________m.
18.如图,某开发区有一块四边形的空地ABCD,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,则要投入________元.
三、解答题
19.在
Rt△ABC
中,∠C=90°,∠A、∠B、∠C
的对边分别为
a、b、c
.
若
a∶c=15∶17,b=24,求
a.
20..《九章算术》中有一道“引葭赴岸”问题:“今有池一丈,葭生其中夹,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:有一个池塘,其底面是边长是10尺的正方形,一根芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B'(如图).水深和芦苇长各多少尺?
21.如图,在边长为4的正方形ABCD中,E是BC的中点,F为CD上一点,且CF=1,判断△AEF是不是直角三角形?试说明理由.
22..《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何 题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点
和点
距离门槛
都为1尺(1尺=10寸),则
的长是多少
23.葛藤是一种刁钻的植物,它的腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一手绝招,就是它绕树盘升时总是沿最短路线螺旋前进,难道植物也懂数学?
通过阅读以_上信息,解决下列问题:
(1)如果树干的周长(即图中圆柱体的底面周长)为30cm,绕一圈升高(即圆柱的高)40cm,则葛藤绕行一圈的最短路程是多少?
(2)如果树干的周长为80cm,绕一圈最短爬行100cm,爬行10圈到达树顶,则树干高多少?
24.勾股定理是人类重大科学发现之一.我国古代数学书《周髀算经》记载,约公元前11世纪,我国古代劳动人民就知道“若勾三,股四,则弦五”,比西方早500多年.请你运用学到的知识、方法和思想探究以下问题.
(1)(探究一)我国汉代数学家赵爽创制了“赵爽弦图”,通过图形切割、拼接,巧妙地利用面积关系证明了勾股定理.古往今来,人们对勾股定理的证明一直保持着极大的热情.意大利著名画家达·芬奇用两张一样的纸片,拼出不一样的空洞,利用空洞面积相等也成功地证明了勾股定理(如图).
请你写出这一证明过程(图中所有的四边形都是正方形,三角形都是直角三角形).
(2)(探究二)在学习勾股定理的过程中,我们获得了以下数学活动经验:分别以直角三角形的三边为边向外侧作正方形(如图2),它们的面积
,
,
之间满足的等量关系是:________.
(3)迁移应用:如图3,图中所有的四边形都是正方形,三角形都是直角三角形.若正方形
,
,
,
的边长分别是
,
,
,
,则正方形
的面积是________.
(4)(探究三)如图4,分别以直角三角形的三边为直径向外侧作半圆,则它们的面积
,
,
之间满足的等量关系是________.
(5)迁移应用:如图5,直角三角形的两条直角边长分别为
,
,斜边长为
,分别以三边为直径作半圆.若
,
,则图中阴影部分的面积等于________.
(6)(探究四)《九章算术》卷九“勾股”中记载:今有立木,系索其末,委地三尺.引索却行,去本八尺而索尺.问索长几何.译文:今有一竖立着的木柱,在木桩的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有
尺.牵着绳索(绳索与地面接触)退行,在距木柱根部
尺处时绳索用尽.问绳索长多少?
答案解析部分
一、单选题
1.【答案】
A
2.【答案】
C
3.【答案】
C
4.【答案】
B
5.【答案】
A
6.【答案】
D
7.【答案】
C
8.【答案】
B
9.【答案】
D
10.【答案】
D
11.【答案】
A
12.【答案】
B
二、填空题
13.【答案】
24
14.【答案】
144
15.【答案】
16.【答案】
如果三角形的两条边的平方和等于第三边的平方,那么这个三角形是直角三角形
17.【答案】
17
18.【答案】
7200
三、解答题
19.【答案】
解:设a=15x,则c=17x,
由勾股定理得,(15x)2+242=(17x)2
,
解得,x=3,
则a=15x=45.
20.【答案】
解:依题意画出图形,如下图,
设芦苇长AB=AB'=x尺,则水深AC=(x-1)尺,
因为B'E=10尺,所以B'C=5尺,
在Rt△ACB'中,52+(x-1)2=x2
,
解得:x=13,
即水深12尺,芦苇长13尺.
21.【答案】
解:△AEF是直角三角形.
理由:∵正方形的边长为4,E是BC的中点,CF=1,
∴DF=3,CE=BE=2.
由勾股定理得:AF2=AD2+DF2=16+9=25,
EF2=CE2+CF2=4+1=5,
AE2=AB2+BE2=16+4=20,
∴AF2=EF2+AE2
,
∴△AEF为直角三角形.
22.【答案】
解:取AB的中点O,过D作DE⊥AB于E,如图2所示:
由题意得:OA=OB=AD=BC,
设OA=OB=AD=BC=r寸,
则AB=2r(寸),DE=10寸,OE=
CD=1寸,
∴AE=(r
1)寸,
在Rt△ADE中,
AE2+DE2=AD2
,
即(r
1)2+102=r2
,
解得:r=50.5,
∴2r=101(寸),
∴AB=101寸.
23.【答案】
(1)解:如图①所示,将圆柱的侧面展开后,该侧面是长方形,AA'=30
cm,高是40
cm,
则A'B'=40
cm,所以AB'2=
AA'2+A'B'2=502
,所以绕行一圈的最短路程为50
cm.
(2)解:如图②所示,因为底面圆的周长为80
cm,即AA'=80
cm,绕一圈最短爬行100
cm,
则AB'
=
100
cm,
在Rt△AB'A'中,因为A'B'2=AB'2-
AA'2=1002-
802=602
,所以A'B'=60
cm,所以树干高=
60×10=
600(cm),600
cm=6
m.
所以树干高为6
m
24.【答案】
(1)由题意得:②的面积为a2+b2+2
ab=a2+b2+ab;
图③的面积为c2+2
ab=c2+ab,
∴a2+b2+ab=c2+ab,
即a2+b2=c2;
(2)S1+S2=S3
(3)47
(4)S1+S2=S3
(5)30
(6)设绳索长为x尺,根据题意得:
x2-(x-3)2=82
,
解得:x=
,
答:绳索长为
尺.
勾股定理》单元检测卷
一、单选题
1.在西方,人们称为毕达哥拉斯定理,在我国把它称为勾股定理,其具体内容指的是(
)
A.如果直角三角形的两条直角边分别为a,b,斜边为c,那么a2+b2=c2
B.如果直角三角形的三边分别为a,b,c,那么a2+b2=c2
C.如果三角形的三边分别为a,b,c,那么a2+b2=c2
D.如果三角形的三边长a,b,c满足a2+b2=c2
,
那么这个三角形是直角三角形
2.一直角三角形两
直角边长分别为5和12,则斜边长为(
)
A.5
B.12
C.13
D.17
3.如图是我校的长方形水泥操场,如果一学生要从A角走到C角,至少走(
)
A.140米
B.120米
C.100米
D.90米
4.如图,由两个直角三角形和三个正方形组成的图形,大直角三角形的斜边和直角边长分别是13,12.则图中阴影部分的面积是(
)
A.16
B.25
C.144
D.169
5..一帆船先向正西航行24千米,然后向正南航行10千米,这时它离出发点有(
)千米.
A. 26 B. 18 C. 13 D. 32
6.下列四组数据不能作为直角三角形的三边长的是(
)
A. 9,12,15 B. 7,24,25 C. 15,36,39 D. 12,15,20
7.已知四个三角形分别满足下列条件:①一个内角等于另两个内角之和;②三个内角度数之比为3∶4∶5;③三边长分别为7,24,25;④三边长之比为5∶12∶13.其中直角三角形有(
)
A.1个
B.2个
C.3个
D.4个
8..在
中,若
,则(
)
A. B. C. D. 不能确定
9.《九章算术》是我国古代第一部数学专著,它的出现标志着中国古代数学形成了完整的体系.“折竹抵地”问题源自《九章算术》中:今有竹高一丈,末折抵地,去根六尺,问折高者几何?意思是一根竹子,原高一丈(一丈=10尺)一阵风将竹子折断,某竹梢恰好抵地,抵地处离竹子底部6尺远,则折断处离地面的高度是(
)
A.5.3尺
B.6.8尺
C.4.7尺
D.3.2尺
10.如图,“今有竹高两丈五尺,末折抵地,去本五尺,问折者高几何?”意思是:一根竹子,原来高两丈五尺(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部五尺远,则折断处离地面的高度为(
)
A.5尺
B.25尺
C.13尺
D.12尺
11.如图,在高为
,坡面长为
的楼梯表面铺地毯,地毯的长度至少需要(
)
A.
B.
C.
D.
12..如图,圆柱形玻璃板,高为12cm
,
底面周长为18cm
,
在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的A处,则蚂蚁到达蜂蜜的最短距离(
)cm
.
A. 14 B. 15 C. 16 D. 17
二、填空题
13.如果一个直角三角形的三边长为三个连续偶数,则它的周长为________.
14.如图,A代表所在的正方形的面积,则A的值是________.
15.如图,在
中,
,则三个半圆面积S1
,
S2
,
S3的关系为________.
16.在没有直角工具之前,聪明的古埃及人用如图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中5这条边所对的角便是直角.依据是________.
17.如图,小亮将升旗的绳子拉到旗杆底端,绳子刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端离地面2m,则旗杆的高度(滑轮上方的部分忽略不计)为________m.
18.如图,某开发区有一块四边形的空地ABCD,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,则要投入________元.
三、解答题
19.在
Rt△ABC
中,∠C=90°,∠A、∠B、∠C
的对边分别为
a、b、c
.
若
a∶c=15∶17,b=24,求
a.
20..《九章算术》中有一道“引葭赴岸”问题:“今有池一丈,葭生其中夹,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:有一个池塘,其底面是边长是10尺的正方形,一根芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B'(如图).水深和芦苇长各多少尺?
21.如图,在边长为4的正方形ABCD中,E是BC的中点,F为CD上一点,且CF=1,判断△AEF是不是直角三角形?试说明理由.
22..《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何 题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点
和点
距离门槛
都为1尺(1尺=10寸),则
的长是多少
23.葛藤是一种刁钻的植物,它的腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一手绝招,就是它绕树盘升时总是沿最短路线螺旋前进,难道植物也懂数学?
通过阅读以_上信息,解决下列问题:
(1)如果树干的周长(即图中圆柱体的底面周长)为30cm,绕一圈升高(即圆柱的高)40cm,则葛藤绕行一圈的最短路程是多少?
(2)如果树干的周长为80cm,绕一圈最短爬行100cm,爬行10圈到达树顶,则树干高多少?
24.勾股定理是人类重大科学发现之一.我国古代数学书《周髀算经》记载,约公元前11世纪,我国古代劳动人民就知道“若勾三,股四,则弦五”,比西方早500多年.请你运用学到的知识、方法和思想探究以下问题.
(1)(探究一)我国汉代数学家赵爽创制了“赵爽弦图”,通过图形切割、拼接,巧妙地利用面积关系证明了勾股定理.古往今来,人们对勾股定理的证明一直保持着极大的热情.意大利著名画家达·芬奇用两张一样的纸片,拼出不一样的空洞,利用空洞面积相等也成功地证明了勾股定理(如图).
请你写出这一证明过程(图中所有的四边形都是正方形,三角形都是直角三角形).
(2)(探究二)在学习勾股定理的过程中,我们获得了以下数学活动经验:分别以直角三角形的三边为边向外侧作正方形(如图2),它们的面积
,
,
之间满足的等量关系是:________.
(3)迁移应用:如图3,图中所有的四边形都是正方形,三角形都是直角三角形.若正方形
,
,
,
的边长分别是
,
,
,
,则正方形
的面积是________.
(4)(探究三)如图4,分别以直角三角形的三边为直径向外侧作半圆,则它们的面积
,
,
之间满足的等量关系是________.
(5)迁移应用:如图5,直角三角形的两条直角边长分别为
,
,斜边长为
,分别以三边为直径作半圆.若
,
,则图中阴影部分的面积等于________.
(6)(探究四)《九章算术》卷九“勾股”中记载:今有立木,系索其末,委地三尺.引索却行,去本八尺而索尺.问索长几何.译文:今有一竖立着的木柱,在木桩的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有
尺.牵着绳索(绳索与地面接触)退行,在距木柱根部
尺处时绳索用尽.问绳索长多少?
答案解析部分
一、单选题
1.【答案】
A
2.【答案】
C
3.【答案】
C
4.【答案】
B
5.【答案】
A
6.【答案】
D
7.【答案】
C
8.【答案】
B
9.【答案】
D
10.【答案】
D
11.【答案】
A
12.【答案】
B
二、填空题
13.【答案】
24
14.【答案】
144
15.【答案】
16.【答案】
如果三角形的两条边的平方和等于第三边的平方,那么这个三角形是直角三角形
17.【答案】
17
18.【答案】
7200
三、解答题
19.【答案】
解:设a=15x,则c=17x,
由勾股定理得,(15x)2+242=(17x)2
,
解得,x=3,
则a=15x=45.
20.【答案】
解:依题意画出图形,如下图,
设芦苇长AB=AB'=x尺,则水深AC=(x-1)尺,
因为B'E=10尺,所以B'C=5尺,
在Rt△ACB'中,52+(x-1)2=x2
,
解得:x=13,
即水深12尺,芦苇长13尺.
21.【答案】
解:△AEF是直角三角形.
理由:∵正方形的边长为4,E是BC的中点,CF=1,
∴DF=3,CE=BE=2.
由勾股定理得:AF2=AD2+DF2=16+9=25,
EF2=CE2+CF2=4+1=5,
AE2=AB2+BE2=16+4=20,
∴AF2=EF2+AE2
,
∴△AEF为直角三角形.
22.【答案】
解:取AB的中点O,过D作DE⊥AB于E,如图2所示:
由题意得:OA=OB=AD=BC,
设OA=OB=AD=BC=r寸,
则AB=2r(寸),DE=10寸,OE=
CD=1寸,
∴AE=(r
1)寸,
在Rt△ADE中,
AE2+DE2=AD2
,
即(r
1)2+102=r2
,
解得:r=50.5,
∴2r=101(寸),
∴AB=101寸.
23.【答案】
(1)解:如图①所示,将圆柱的侧面展开后,该侧面是长方形,AA'=30
cm,高是40
cm,
则A'B'=40
cm,所以AB'2=
AA'2+A'B'2=502
,所以绕行一圈的最短路程为50
cm.
(2)解:如图②所示,因为底面圆的周长为80
cm,即AA'=80
cm,绕一圈最短爬行100
cm,
则AB'
=
100
cm,
在Rt△AB'A'中,因为A'B'2=AB'2-
AA'2=1002-
802=602
,所以A'B'=60
cm,所以树干高=
60×10=
600(cm),600
cm=6
m.
所以树干高为6
m
24.【答案】
(1)由题意得:②的面积为a2+b2+2
ab=a2+b2+ab;
图③的面积为c2+2
ab=c2+ab,
∴a2+b2+ab=c2+ab,
即a2+b2=c2;
(2)S1+S2=S3
(3)47
(4)S1+S2=S3
(5)30
(6)设绳索长为x尺,根据题意得:
x2-(x-3)2=82
,
解得:x=
,
答:绳索长为
尺.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
