沪教版(上海)高中数学高一下册 5.1 任意角及其度量 课件1(共25张PPT)
文档属性
| 名称 | 沪教版(上海)高中数学高一下册 5.1 任意角及其度量 课件1(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 22:24:31 | ||
图片预览






文档简介
(共25张PPT)
目标:
1、理解并掌握弧度制的定义,
2、能进行角度与弧度之间的换算。
3、能用弧度制解决简单的问题
温故而知新
1、角度制的定义
规定周角的1/360为1度的角这种用度做单位来度量角的制度叫角度制。
1°
2、弧长公式及扇形面积公式
nπR
180
l=
———
nπR2
360
S=
———
n°
R
l
1、弧度制
我们把等于半径长的圆弧所对的圆心角
叫做1弧度的角。
设弧AB的长为l,
若l=r,则∠AOB=
1
弧度
l
r
=
O
B
r
l=r
A
1弧度
讲授新课
则∠AOB=
2
弧度
l
r
=
则∠AOB=
2π弧度
l
r
=
r
O
A
B
l=2r
2π弧度
l=2
π
r
O
A
(B)
r
若l=2r,
若l=2
π
r,
2弧度
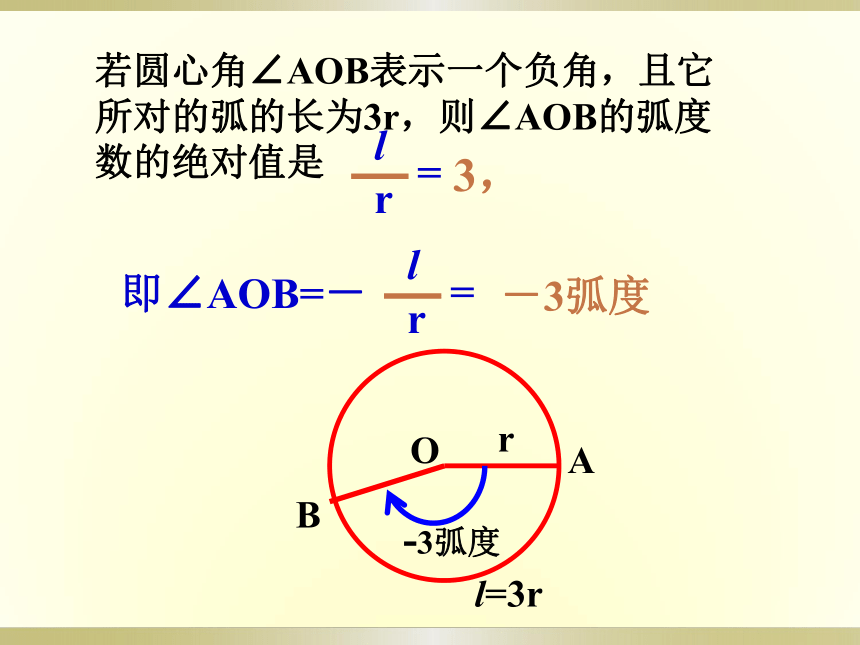
若圆心角∠AOB表示一个负角,且它
所对的弧的长为3r,则∠AOB的弧度
数的绝对值是
l
r
=
3,
即∠AOB=-
l
r
=
-3弧度
l=3r
O
A
B
r
-3弧度
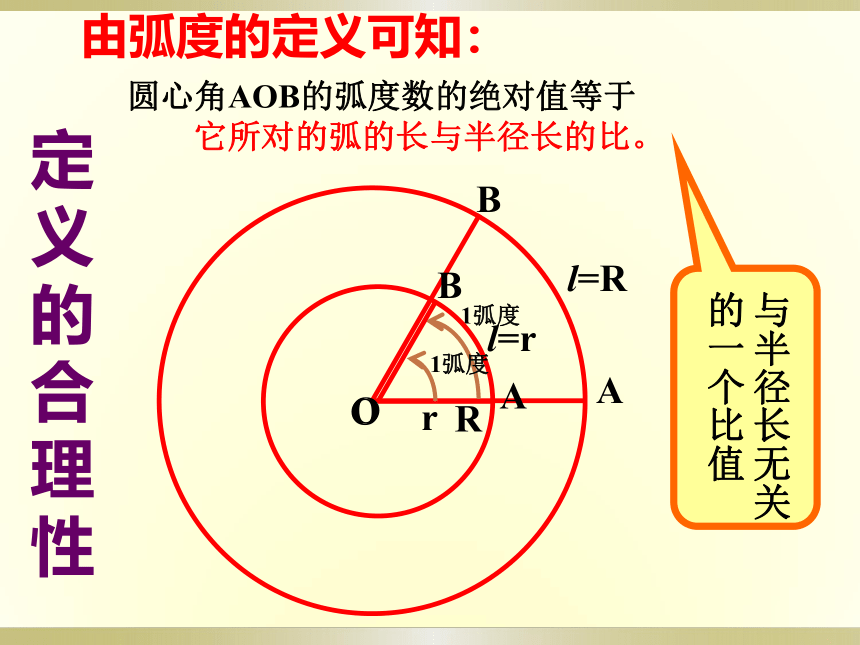
由弧度的定义可知:
圆心角AOB的弧度数的绝对值等于
它所对的弧的长与半径长的比。
定义的合理性
1弧度
R
l=R
O
A
B
1弧度
r
l=r
O
A
B
与半径长无关
的一个比值
一般地,我们规定:
正角的弧度数为正数,负角的弧度数为负数,
零角的弧度数为零,任一已知角α的弧度数的绝对值:
︱α︱=
l
r
其中l为以角α作为圆心角时所对圆弧的长,r
为圆的半径。这种用“弧度”
做单位来度量角的
制度叫做弧度制。
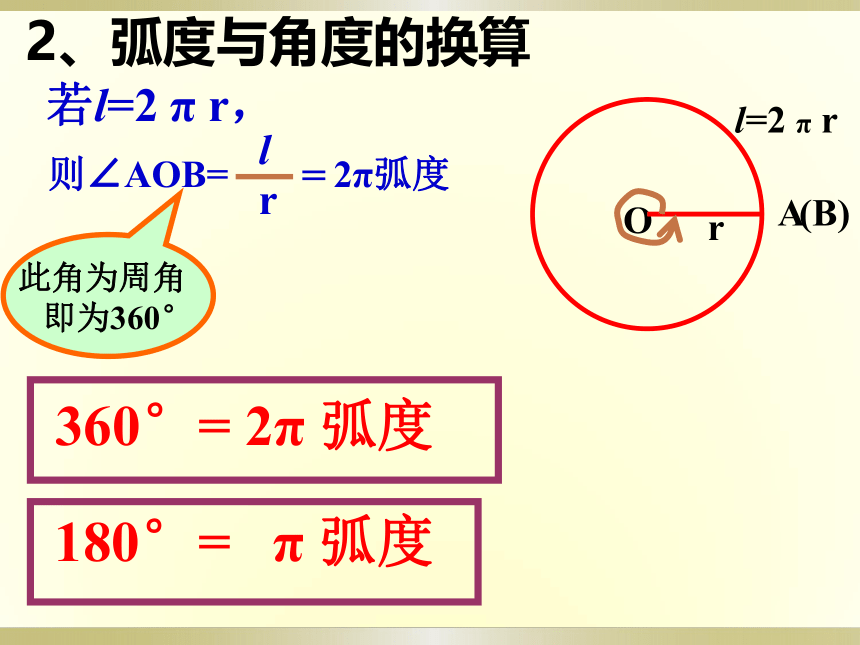
2、弧度与角度的换算
l
r
=
则∠AOB=
2π弧度
此角为周角
即为360°
360°=
2π
弧度
180°=
π
弧度
l=2
π
r
O
A
(B)
r
若l=2
π
r,
由180°=
π
弧度
还可得
1°=
——
弧度
≈
0.01745弧度
180
π
1弧度
=(——)°≈
57.30°=
57°18′
π
180
3、例题
例1.
把下列各角化成弧度
(1)
67
°30'
(2)
120
°
(3)
75
°
(4)
135
°
(5)
300
°
(6)
-
210
°
例2:
把下列各弧度化成度.
(2)
(3)
(4)
(1)108o
(2)15o
(3)-144o
(4)-150o
注:
1、对于一些特殊角的度数与弧度数
之间的换算要熟记。
度
0°
30
°
45
°
60
°
90
°
180
°
270°
360°
弧度
0
π
2π
π
6
π
2
π
4
π
3
π
3
2
2、用弧度为单位表示角的大小时,“弧度”二字通常省略不写,但用“度”(°)为单位不能省。
3、用弧度为单位表示角时,通常写成“多少π”的形式。
例3、把下列各角化成 的形式:
(1) ;(2) ;(3) .
(1):
(3):
(2):
4、圆的弧长公式及扇形面积公式
α
O
l
r
l
=︱α
︱r
由︱α︱=
l
r
得
S
=
—
l
r
1
2
=
—︱α
︱r2
1
2
5、用弧度来度量角,实际上角的集合
与实数集R之间建立一一对应的关系:
实数集R
角的集合
正角
零角
负角
正实数
零
负实数
对应角的弧度数
练习、下列角的终边相同的是( ).
A.
与
与
与
与
B.
C.
D.
B
练习
x
y
0
(1)
x
y
0
(2)
练习
小结:
1、量角的制度:角度制与弧度制
弧度制除了使角与实数有一一对应关系外,
为以后学习三角函数打下基础。
2、能熟练地进行角度与弧度之间的换算。
3、弧长公式:
扇形面积公式:
(其中
为圆心角
所对的弧长,
为圆心角的弧度数)
写出满足下列条件的角的集合(用弧度制):
1、
终边与X轴正半轴重合;
2、
终边与X轴负半轴重合;
3、
终边与X轴重合;
4、
终边与Y轴正半轴重合;
5、
终边与Y轴负半轴重合;
6、
终边与Y轴重合;
7、第一象限内的角;
8、第二象限内的角;
9、第三象限内的角;
10、第四象限内的角;
目标:
1、理解并掌握弧度制的定义,
2、能进行角度与弧度之间的换算。
3、能用弧度制解决简单的问题
温故而知新
1、角度制的定义
规定周角的1/360为1度的角这种用度做单位来度量角的制度叫角度制。
1°
2、弧长公式及扇形面积公式
nπR
180
l=
———
nπR2
360
S=
———
n°
R
l
1、弧度制
我们把等于半径长的圆弧所对的圆心角
叫做1弧度的角。
设弧AB的长为l,
若l=r,则∠AOB=
1
弧度
l
r
=
O
B
r
l=r
A
1弧度
讲授新课
则∠AOB=
2
弧度
l
r
=
则∠AOB=
2π弧度
l
r
=
r
O
A
B
l=2r
2π弧度
l=2
π
r
O
A
(B)
r
若l=2r,
若l=2
π
r,
2弧度
若圆心角∠AOB表示一个负角,且它
所对的弧的长为3r,则∠AOB的弧度
数的绝对值是
l
r
=
3,
即∠AOB=-
l
r
=
-3弧度
l=3r
O
A
B
r
-3弧度
由弧度的定义可知:
圆心角AOB的弧度数的绝对值等于
它所对的弧的长与半径长的比。
定义的合理性
1弧度
R
l=R
O
A
B
1弧度
r
l=r
O
A
B
与半径长无关
的一个比值
一般地,我们规定:
正角的弧度数为正数,负角的弧度数为负数,
零角的弧度数为零,任一已知角α的弧度数的绝对值:
︱α︱=
l
r
其中l为以角α作为圆心角时所对圆弧的长,r
为圆的半径。这种用“弧度”
做单位来度量角的
制度叫做弧度制。
2、弧度与角度的换算
l
r
=
则∠AOB=
2π弧度
此角为周角
即为360°
360°=
2π
弧度
180°=
π
弧度
l=2
π
r
O
A
(B)
r
若l=2
π
r,
由180°=
π
弧度
还可得
1°=
——
弧度
≈
0.01745弧度
180
π
1弧度
=(——)°≈
57.30°=
57°18′
π
180
3、例题
例1.
把下列各角化成弧度
(1)
67
°30'
(2)
120
°
(3)
75
°
(4)
135
°
(5)
300
°
(6)
-
210
°
例2:
把下列各弧度化成度.
(2)
(3)
(4)
(1)108o
(2)15o
(3)-144o
(4)-150o
注:
1、对于一些特殊角的度数与弧度数
之间的换算要熟记。
度
0°
30
°
45
°
60
°
90
°
180
°
270°
360°
弧度
0
π
2π
π
6
π
2
π
4
π
3
π
3
2
2、用弧度为单位表示角的大小时,“弧度”二字通常省略不写,但用“度”(°)为单位不能省。
3、用弧度为单位表示角时,通常写成“多少π”的形式。
例3、把下列各角化成 的形式:
(1) ;(2) ;(3) .
(1):
(3):
(2):
4、圆的弧长公式及扇形面积公式
α
O
l
r
l
=︱α
︱r
由︱α︱=
l
r
得
S
=
—
l
r
1
2
=
—︱α
︱r2
1
2
5、用弧度来度量角,实际上角的集合
与实数集R之间建立一一对应的关系:
实数集R
角的集合
正角
零角
负角
正实数
零
负实数
对应角的弧度数
练习、下列角的终边相同的是( ).
A.
与
与
与
与
B.
C.
D.
B
练习
x
y
0
(1)
x
y
0
(2)
练习
小结:
1、量角的制度:角度制与弧度制
弧度制除了使角与实数有一一对应关系外,
为以后学习三角函数打下基础。
2、能熟练地进行角度与弧度之间的换算。
3、弧长公式:
扇形面积公式:
(其中
为圆心角
所对的弧长,
为圆心角的弧度数)
写出满足下列条件的角的集合(用弧度制):
1、
终边与X轴正半轴重合;
2、
终边与X轴负半轴重合;
3、
终边与X轴重合;
4、
终边与Y轴正半轴重合;
5、
终边与Y轴负半轴重合;
6、
终边与Y轴重合;
7、第一象限内的角;
8、第二象限内的角;
9、第三象限内的角;
10、第四象限内的角;
