沪教版(上海)高中数学高一下册 6.3 函数y=Asin(ωx+φ)的图像与性质 课件1(共26张PPT)
文档属性
| 名称 | 沪教版(上海)高中数学高一下册 6.3 函数y=Asin(ωx+φ)的图像与性质 课件1(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 00:00:00 | ||
图片预览



文档简介
(共26张PPT)
函数y=Asin(ωx+φ)的图像与性质
函数y=Asin(ωx+φ)
(其中A>0,
ω>0)
目标:了解并掌握A,ω,φ对函
数图像及性质的影响
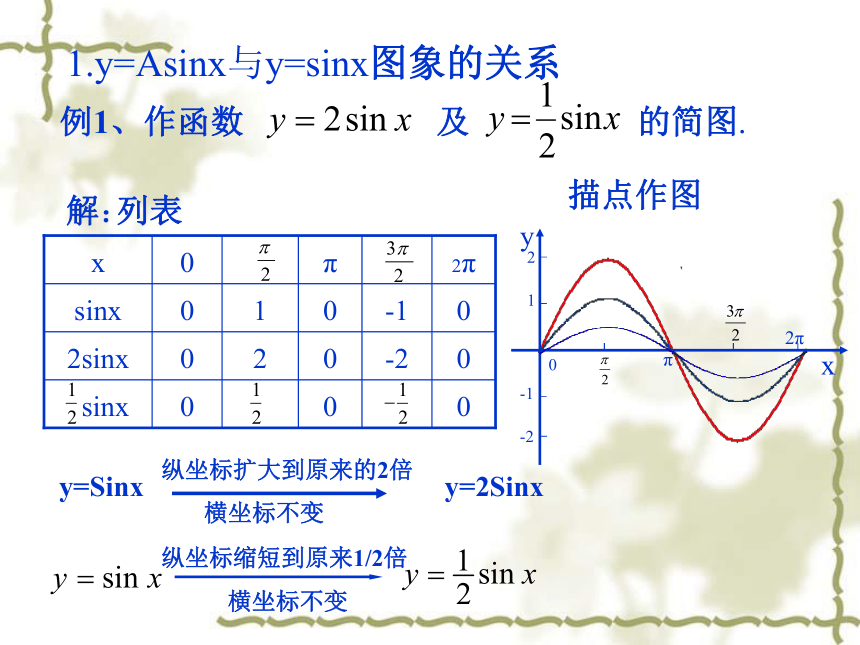
1.y=Asinx与y=sinx图象的关系
解:
列表
0
0
0
sinx
0
-2
0
2
0
2sinx
0
-1
0
1
0
sinx
2π
π
0
x
描点作图
x
y
0
1
2
-1
-2
π
2π
例1、作函数
及
的简图.
横坐标不变
纵坐标缩短到原来1/2倍
y=Sinx
y=2Sinx
纵坐标扩大到原来的2倍
横坐标不变
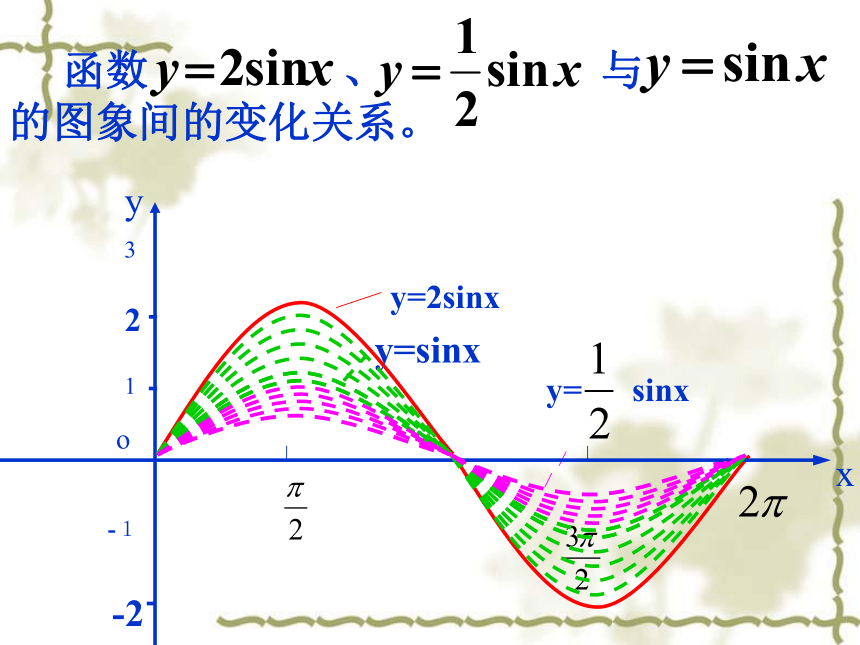
函数
、
与
的图象间的变化关系。
y=sinx
y=2sinx
y=
sinx
1
-1
2
-2
o
x
y
3
-3
函数y=Asin
x
(A
>0且A≠1)的图象可以看作是把
y=sin
x
的图象上所有点的纵坐标伸长
(当A>1时)或缩短(当0到原来的A倍(横坐标不变)
而得到的.
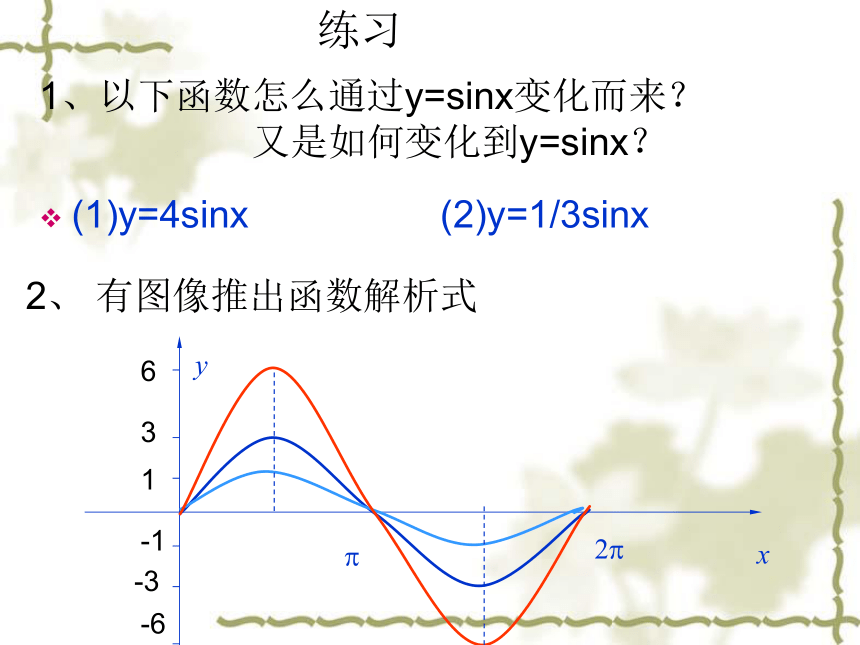
1、以下函数怎么通过y=sinx变化而来?
又是如何变化到y=sinx?
(1)y=4sinx
(2)y=1/3sinx
2、
有图像推出函数解析式
-3
1
3
6
-1
-6
x
y
2
练习
x
y
O
2
1
2
2
1
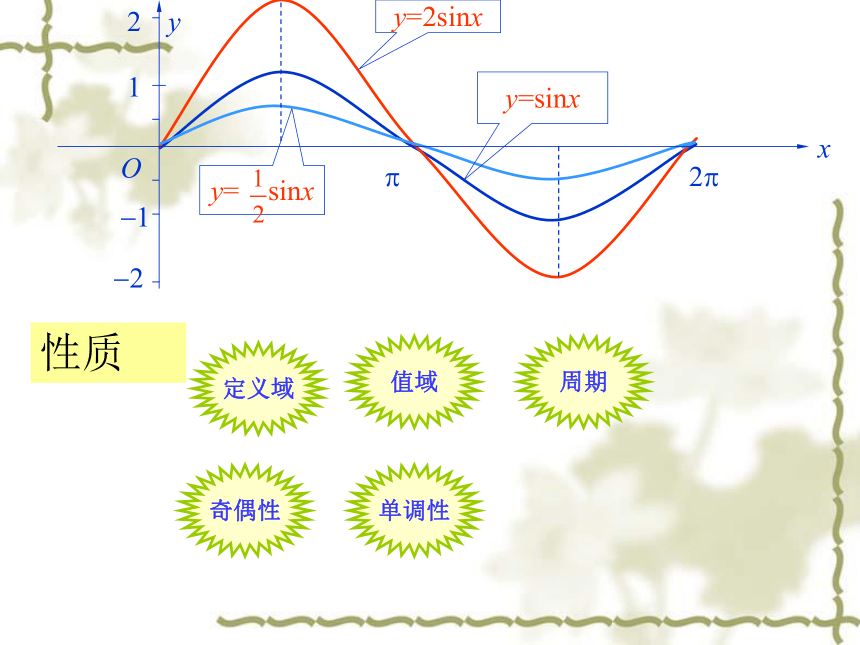
y=2sinx
y=sinx
y=
sinx
性质
定义域
值域
周期
奇偶性
单调性
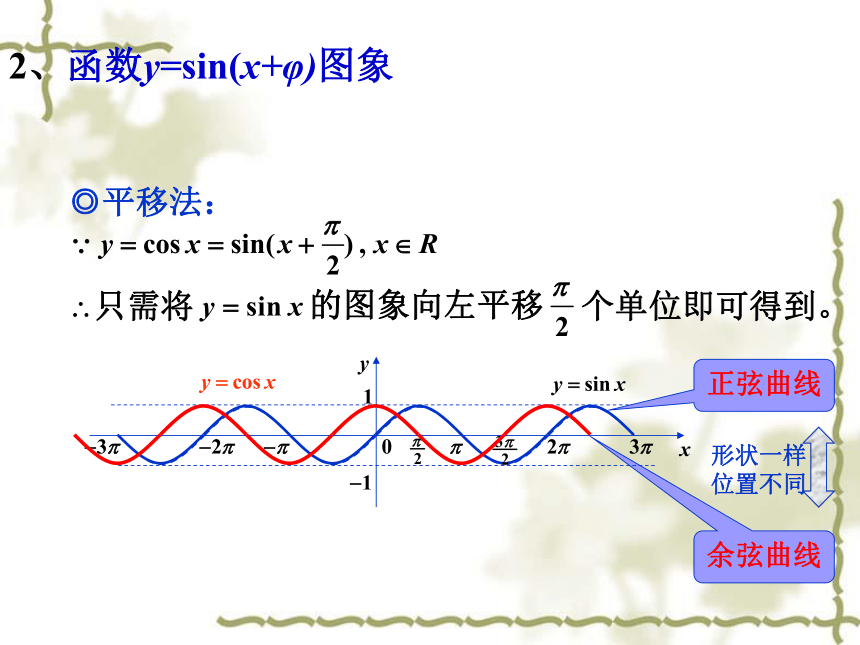
◎平移法:
只需将
的图象向左平移
个单位即可得到。
余弦曲线
正弦曲线
形状一样位置不同
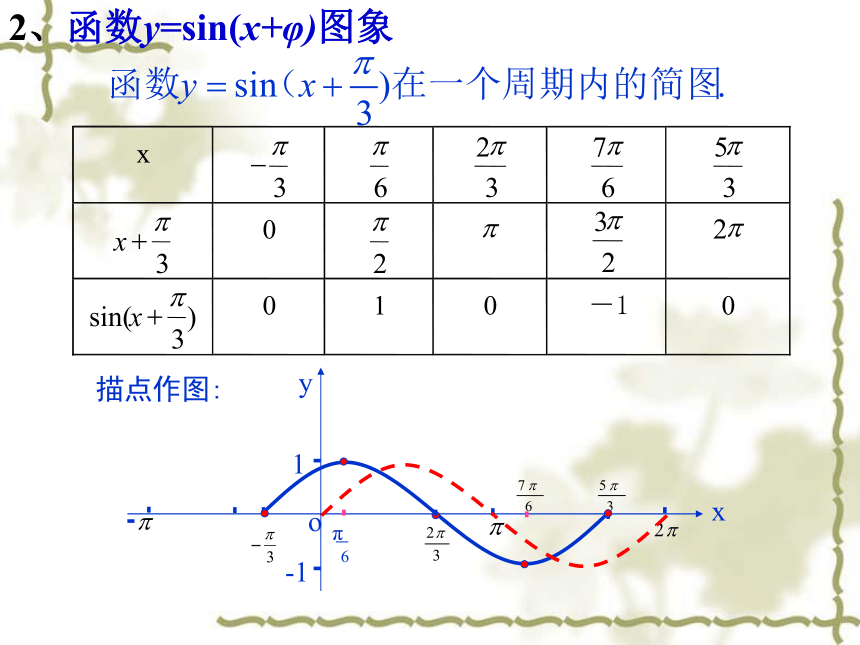
2、函数y=sin(x+φ)图象
x
x
+
p
3
0
p
2
p
3
2
p
2
p
sin(
)
x
+
p
3
0
1
0
-1
0
-
p
3
p
6
2
3
p
7
6
p
5
3
p
o
x
1
-1
y
π
6
描点作图:
2、函数y=sin(x+φ)图象
0
0
-1
0
1
y
O
x
-1
1
描点作图:
y
O
x
-1
1
对于φ取不同的值情况如何呢?
函数y=sin(x+φ)
的图象可以看作是把
y=sin
x
的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平移|φ|个单位而得到的.
结论二:
x
O
2
1
1
练习
1、以下函数怎么通过y=sinx变化而来?
又是如何变化到y=sinx?
2、
有图像推出函数解析式
(1)y=sin(x+
/6)
(2)
y=sin(x-
/4)
y
O
x
-1
1
性质:定义域、值域、周期、奇偶性、单调性
1.列表:
x
例2.作函数
及
的图象。
x
O
y
2
1
2
2
1
3
2.
描点:
y=sinx
y=sin2x
y=sin2x
y=sinx
纵坐标不变
,横坐标
缩短为原来的1/2倍
3.
Y=sin
x
与
y=sinx图象的关系
1.
列表:
x
y
O
2
1
1
3
4
2.
描点:
y=sin
x
2
1
y=sinx
0
p
2π
3π
4p
0
2
p
p
2
3
p
2π
x
x
2
1
x
2
1
sin
-1
0
1
0
0
y=
sin
x
y=sinx
2
1
纵坐标不变,
横坐标
变为原来的
2
倍
函数
、
与
的图象间的变化关系。
1
-1
o
x
y
2
-3
函数y=sin x
(
>0且 ≠1)的图象可以看作是把
y=sinx
的图象上所有点的横坐标缩短(当 >1时)或伸长(当0< <1时)
到原来的
倍(纵坐标不变)
而得到的。
函数y=sin x( >0)图象
结论三
练习
1、以下函数怎么通过y=sinx变化而来?
又是如何变化到y=sinx?
(1)y=sin4x
(2)
y=sin3/2x
2、y=3sin(2x+
)函数相关概念
周期
频率
振幅
4
、函数y=Asin(
x+
)的图象
作出y=3sin(2x+
)的图象。
问题
x
2x+
3sin(2x+
)
0
3
0
-3
0
0
2
_
y
3
2
-2
-3
x
1
o
-1
-
y=3sin(2x+
)
3
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x+ )
y=3sin(2x+ )
方法1:
y=sin(x+ )
y=sinx
先左右平移再左右伸缩(只变x的系数)
函数
y=sinx
y=sin(x+
)
的图象
(3)横坐标不变
纵坐标伸长到原来的3倍
y=3sin(2x+
)的图象
y=sin(2x+
)
的图象
(1)向左平移
纵坐标不变
(2)横坐标缩短到原来的
倍
步骤1
步骤2
步骤3
步骤4
步骤5
沿x轴
平行移动
横坐标
伸长或缩短
纵坐标
伸长或缩短
沿x轴
扩展
y
3
2
-2
-3
1
x
o
-1
-
y=sinx
y=sin2x
y=3sin(2x+
)
兀
3
先左右伸缩再左右平移(注意变形)
变换2:
y
=sin2(x+
)
兀
6
=sin(2x+
)
兀
3
函数y=Asin(ωx+φ)的图像与性质
函数y=Asin(ωx+φ)
(其中A>0,
ω>0)
目标:了解并掌握A,ω,φ对函
数图像及性质的影响
1.y=Asinx与y=sinx图象的关系
解:
列表
0
0
0
sinx
0
-2
0
2
0
2sinx
0
-1
0
1
0
sinx
2π
π
0
x
描点作图
x
y
0
1
2
-1
-2
π
2π
例1、作函数
及
的简图.
横坐标不变
纵坐标缩短到原来1/2倍
y=Sinx
y=2Sinx
纵坐标扩大到原来的2倍
横坐标不变
函数
、
与
的图象间的变化关系。
y=sinx
y=2sinx
y=
sinx
1
-1
2
-2
o
x
y
3
-3
函数y=Asin
x
(A
>0且A≠1)的图象可以看作是把
y=sin
x
的图象上所有点的纵坐标伸长
(当A>1时)或缩短(当0
而得到的.
1、以下函数怎么通过y=sinx变化而来?
又是如何变化到y=sinx?
(1)y=4sinx
(2)y=1/3sinx
2、
有图像推出函数解析式
-3
1
3
6
-1
-6
x
y
2
练习
x
y
O
2
1
2
2
1
y=2sinx
y=sinx
y=
sinx
性质
定义域
值域
周期
奇偶性
单调性
◎平移法:
只需将
的图象向左平移
个单位即可得到。
余弦曲线
正弦曲线
形状一样位置不同
2、函数y=sin(x+φ)图象
x
x
+
p
3
0
p
2
p
3
2
p
2
p
sin(
)
x
+
p
3
0
1
0
-1
0
-
p
3
p
6
2
3
p
7
6
p
5
3
p
o
x
1
-1
y
π
6
描点作图:
2、函数y=sin(x+φ)图象
0
0
-1
0
1
y
O
x
-1
1
描点作图:
y
O
x
-1
1
对于φ取不同的值情况如何呢?
函数y=sin(x+φ)
的图象可以看作是把
y=sin
x
的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平移|φ|个单位而得到的.
结论二:
x
O
2
1
1
练习
1、以下函数怎么通过y=sinx变化而来?
又是如何变化到y=sinx?
2、
有图像推出函数解析式
(1)y=sin(x+
/6)
(2)
y=sin(x-
/4)
y
O
x
-1
1
性质:定义域、值域、周期、奇偶性、单调性
1.列表:
x
例2.作函数
及
的图象。
x
O
y
2
1
2
2
1
3
2.
描点:
y=sinx
y=sin2x
y=sin2x
y=sinx
纵坐标不变
,横坐标
缩短为原来的1/2倍
3.
Y=sin
x
与
y=sinx图象的关系
1.
列表:
x
y
O
2
1
1
3
4
2.
描点:
y=sin
x
2
1
y=sinx
0
p
2π
3π
4p
0
2
p
p
2
3
p
2π
x
x
2
1
x
2
1
sin
-1
0
1
0
0
y=
sin
x
y=sinx
2
1
纵坐标不变,
横坐标
变为原来的
2
倍
函数
、
与
的图象间的变化关系。
1
-1
o
x
y
2
-3
函数y=sin x
(
>0且 ≠1)的图象可以看作是把
y=sinx
的图象上所有点的横坐标缩短(当 >1时)或伸长(当0< <1时)
到原来的
倍(纵坐标不变)
而得到的。
函数y=sin x( >0)图象
结论三
练习
1、以下函数怎么通过y=sinx变化而来?
又是如何变化到y=sinx?
(1)y=sin4x
(2)
y=sin3/2x
2、y=3sin(2x+
)函数相关概念
周期
频率
振幅
4
、函数y=Asin(
x+
)的图象
作出y=3sin(2x+
)的图象。
问题
x
2x+
3sin(2x+
)
0
3
0
-3
0
0
2
_
y
3
2
-2
-3
x
1
o
-1
-
y=3sin(2x+
)
3
1
-1
2
-2
o
x
y
3
-3
2
y=sin(2x+ )
y=3sin(2x+ )
方法1:
y=sin(x+ )
y=sinx
先左右平移再左右伸缩(只变x的系数)
函数
y=sinx
y=sin(x+
)
的图象
(3)横坐标不变
纵坐标伸长到原来的3倍
y=3sin(2x+
)的图象
y=sin(2x+
)
的图象
(1)向左平移
纵坐标不变
(2)横坐标缩短到原来的
倍
步骤1
步骤2
步骤3
步骤4
步骤5
沿x轴
平行移动
横坐标
伸长或缩短
纵坐标
伸长或缩短
沿x轴
扩展
y
3
2
-2
-3
1
x
o
-1
-
y=sinx
y=sin2x
y=3sin(2x+
)
兀
3
先左右伸缩再左右平移(注意变形)
变换2:
y
=sin2(x+
)
兀
6
=sin(2x+
)
兀
3
