沪教版(上海)高中数学高一下册 第4章 幂函数、指数函数和对数函数(下) 复习课件(共45张PPT)
文档属性
| 名称 | 沪教版(上海)高中数学高一下册 第4章 幂函数、指数函数和对数函数(下) 复习课件(共45张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 00:00:00 | ||
图片预览







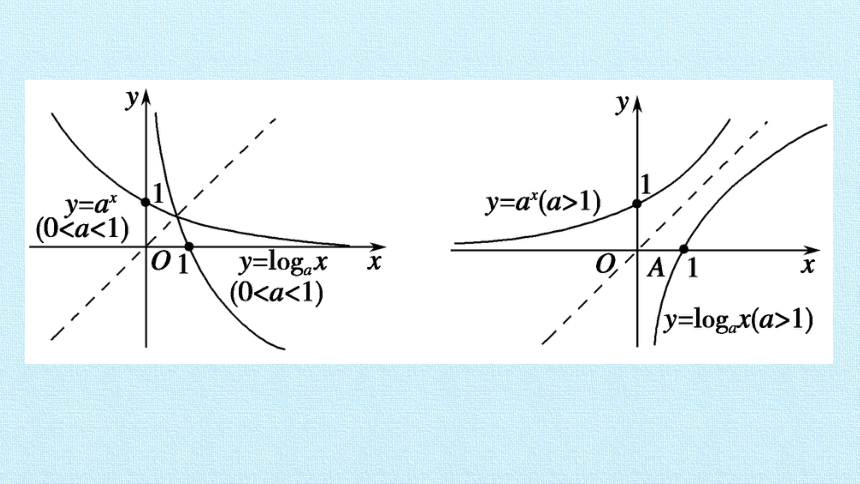



文档简介
(共45张PPT)
第4章
幂函数、指数函数和对数函数(下)
复习课件
1
知识网络
系统盘点,提炼主干
2
要点归纳
整合要点,诠释疑点
3
题型研修
突破重点,提升能力
章末复习提升
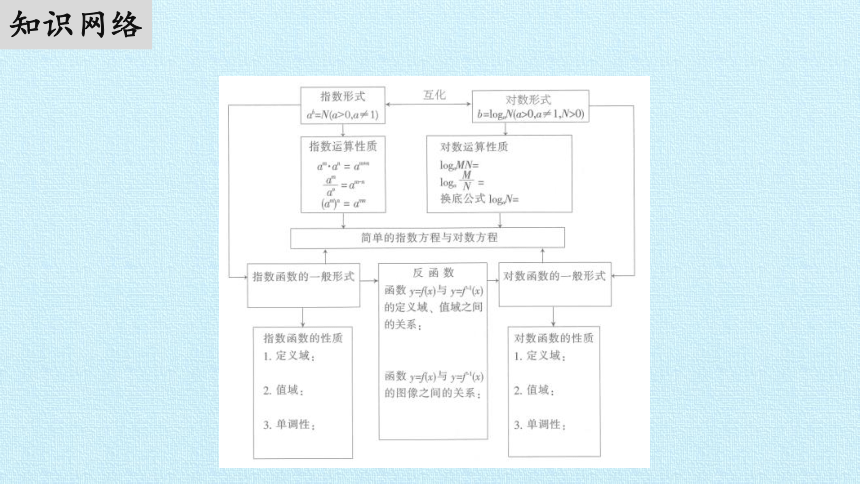
知识网络
1.指数和对数
(1)分数指数的定义:
要点归纳
(2)如同减法是加法的逆运算,除法是乘法的逆运算一样,对数运算是指数运算的逆运算。
ab=N logaN>0,a≠1,N>0).
由此可得到对数=b(a恒等式:
alogaN=N,b=logaab.
(3)对数换底公式logaN=
(a>0,b>0,a≠1,b≠1,N>0)的意义在于把各个不同底数的对数换成相同底数的对数,这样,一可以进行换算,二可以通过对数表求值。
(4)指数和对数的运算法则有:
am·an=am+n,logaM+logaN=loga(MN),
(am)n=amn,logaMn=nlogaM,
(a∈R+,m,n∈R)(M,N∈R+,a>0,a≠1).
2.指数函数、对数函数
(1)要熟记这二个函数在不同条件下的图象,并能熟练地由图象“读”出该函数的主要性质;
(2)同底数的指数函数和对数函数的图象关于直线y=x成轴对称图形。由图可“读”出指数函数和对数函数的主要性质:
指数函数
对数函数
(1)定义域:R
(1)定义域:R+
(2)值域:R+
(2)值域:R
(3)过点(0,1)
(3)过点(1,0)
(4)a>1时为增函数,
0<a<1时为减函数。
(4)a>1时为增函数,
0<a<1时为减函数。
如果两个函数y=f(x)和x=g(y)描述的是同一个对应法则,则称这两个函数互为反函数.这时两者之间满足关系g(f(x))=x和f(g(y))=y,并且它们的图象关于直线y=x成轴对称.函数f叫作g的反函数,g也叫作f的反函数.f的定义域是g的值域,f的值域是g的定义域,两者同为递增或递减。
由上面反函数的定义,我们知道,指数函数y=ax(a>0且a≠1)和同底数的对数函数y=logax(a>0且a≠1)互为反函数。这给研究对数函数的图象和性质带来了方便。
4.函数模型及其应用
(1)目前我们能建立的函数模型主要是一次函数,二次函数,幂函数,指数函数和对数函数的模型;
(2)建模的目的是:模拟实际问题和用模拟函数的性质去推测判断未进行测量或不便测量的数据,特别是实际问题的未来走势;
(3)建模的大致步骤是:了解和简化实际问题,建立实际问题的数学模型,分析所得数学模型,把模型所判断的结论和实际模型的表现加以比较,改进数学模型。
题型一 有关指数、对数的运算问题
指数与指数运算、对数与对数运算是两个重要的知识点,不仅是本章考查的重要题型,也是高考的必考内容。
指数式的运算首先要注意化简顺序,一般负指数先转化成正指数,根式化为指数式;其次若出现分式,则要注意把分子、分母因式分解以达到约分的目的对数运算首先要注意公式应用过程中范围的变化,前后要等价;其次要熟练地运用对数的三个运算性质,并根据具体问题合理利用对数恒等式和换底公式等。换底公式是对数计算、化简、证明常用的公式,一定要掌握并灵活运用。
题型研修
=log39-9=2-9=-7.
题型二 指数函数、对数函数及幂函数的图象与性质
函数的图象是研究函数性质的前提和基础,它较形象直观地反映了函数的一切性质。教材对幂、指、对三个函数的性质的研究也正好体现了由图象到性质,由具体到抽象的过程,突出了函数图象在研究相应函数性质时的作用。
例2 已知函数f(x)是定义在R上的偶函数,当x≥0时,
(1)画出函数f(x)的图象;
解 先作出当x≥0时,f(x)=
x的图象,利用偶函数的图象关于y轴对称,再作出f(x)在x∈(-∞,0)时的图象.
(2)根据图象写出f(x)的单调区间,并写出函数的值域。
解 函数f(x)的单调递增区间为(-∞,0),
单调递减区间为[0,+∞),值域为(0,1].
跟踪演练2 (1)函数f(x)=ln
x的图象与函数g(x)=x2-4x+4的图象的交点个数为( )
A.0
B.1
C.2
D.3
解析 作出两个函数的图象,利用数形结合思想求解。
g(x)=x2-4x+4=(x-2)2,在同一平面
直角坐标系内画出函数f(x)=ln
x与
g(x)=(x-2)2的图象(如图),
由图可得两个函数的图象有2个交点。
C
解析 由3x-1≠0得x≠0,
但从选项D的函数图象可以看出函数在(0,+∞)上是单调递增函数,两者矛盾,可排除选项D,故选C。
答案 C
题型三 比较大小
比较几个数的大小问题是指数函数、对数函数和幂函数的重要应用,其基本方法是:将需要比较大小的几个数视为某类函数的函数值,其主要方法可分以下三种:
(1)根据函数的单调性(如根据一次函数、二次函数、指数函数、对数函数、幂函数的单调性),利用单调性的定义求解;
(2)采用中间量的方法(实际上也要用到函数的单调性),常用的中间量如0,1,-1等;
(3)采用数形结合的方法,通过函数的图象解决。
A.a<b<c
B.c<b<a
C.c<a<b
D.b<a<c
故有a<b<c.
A
跟踪演练3 (1)下列不等式成立的是( )
A.log32<log23<log25
B.log32<log25<log23
C.log23<log32<log25
D.log23<log25<log32
解析 由于log31<log32<log33,
log22<log23<log25,
即0<log32<1,1<log23<log25,
所以log32<log23<log25.故选A.
A
A.x>y>z
B.z>y>x
C.y>x>z
D.z>x>y
C
题型四 简单指数方程和对数方程的解法
通过理解指数方程、对数方程的概念,灵活运用指数函数与对数函数的性质,对简单的指数方程和对数方程进行求解,解决一些简单的实际问题。
A.1
B.9
C.25
D.125
D
题型五 分类讨论思想
本章常见分类讨论思想的应用如下表:
问题
讨论标准
分类情况
比较af(x)与ag(x)的大小
a与1的大小关系
(1)a>1时,若f(x)>g(x),则af(x)>ag(x);
(2)0<a<1时,若f(x)>g(x),则af(x)<ag(x).
解不等式af(x)>ag(x)
a与1的大小关系
(1)a>1时,f(x)>g(x);
(2)0<a<1时,f(x)<g(x).
比较logax1与logax2的大小
a与1的大小关系
(1)a>1时,若x1>x2,则logax1>logax2;
(2)0<a<1时,若x1>x2,则logax1<logax2.
解不等式logaf(x)>logag(x)
a与1的大小关系
(1)a>1时,f(x)>g(x)>0;
(2)0<a<1时,0<f(x)<g(x).
例5 已知偶函数f(x)在x∈[0,+∞)上是增函数,f
=0,求不等式f(logax)>0(a>0,且a≠1)的解集.
解 ∵f(x)是偶函数,且f(x)在[0,+∞)上是增函数,
题型六 函数的实际应用问题
利用给定的函数模型或建立确定的函数模型解决实际问题的方法:
(1)根据题意选用恰当的函数模型来描述所涉及的数量之间的关系;
(2)利用待定系数法,确定具体函数模型;
(3)对所选定的函数模型进行适当的评价、比较,并选择最恰当的模型;
(4)根据实际问题对模型进行适当的修正。
题型六 函数的实际应用问题
例6
某跨国饮料公司在对全世界所有人均GDP(即人均纯收入)在0.5千美元~8千美元的地区销售该公司A饮料的情况的调查中发现:人均GDP处在中等的地区对该饮料的销售量最多,然后向两边递减.
(1)下列几个模拟函数中(x表示人均GDP,单位:千美元,y表示A饮料的年人均销量,单位:升),用哪个模拟函数来描述A饮料的年人均销量与地区的人均GDP关系更合适 说明理由.y=ax2+bx,y=kx+b,y=logax+b,y=ax+b.
解
(1)用函数y=ax2+bx来描述A饮料的年人均销量与地区的人均GDP的关
系更合适。因为函数y=kx+b,y=logax+b,y=ax+b在其定义域内都是单调函数,不具备先递增后递减的特征。
(2)若人均GDP为1千美元时,A饮料的年人均销量为2升;若人均GDP为4千美元时,A饮料的年人均销量为5升,把(1)中你所选的模拟函数求出来,并求出各个地区中,A饮料的年人均销量最多是多少
课堂小结
1.函数是高中数学极为重要的内容,函数思想和函数方法贯穿高中数学的整个过程,纵观历年高考试题,对本章的考查是以基本函数形式出现的综合题和应用题,一直是常考不衰的热点问题。
2.从考查角度看,指数函数、对数函数概念的考查以基本概念与基本计算为主;对图象的考查重在考查平移变换、对称变换以及利用数形结合的思想方法解决数学问题的能力;对幂函数的考查将会从概念、图象、性质等方面来考查。
3.对于简单的指数方程和对数方程,借助两者函数的性质可进行计算求解。
4.函数模型的应用实例的基本题型:
(1)给定函数模型解决实际问题;
(2)建立确定性的函数模型解决问题;
(3)建立拟合函数模型解决实际问题。
谢
谢
第4章
幂函数、指数函数和对数函数(下)
复习课件
1
知识网络
系统盘点,提炼主干
2
要点归纳
整合要点,诠释疑点
3
题型研修
突破重点,提升能力
章末复习提升
知识网络
1.指数和对数
(1)分数指数的定义:
要点归纳
(2)如同减法是加法的逆运算,除法是乘法的逆运算一样,对数运算是指数运算的逆运算。
ab=N logaN>0,a≠1,N>0).
由此可得到对数=b(a恒等式:
alogaN=N,b=logaab.
(3)对数换底公式logaN=
(a>0,b>0,a≠1,b≠1,N>0)的意义在于把各个不同底数的对数换成相同底数的对数,这样,一可以进行换算,二可以通过对数表求值。
(4)指数和对数的运算法则有:
am·an=am+n,logaM+logaN=loga(MN),
(am)n=amn,logaMn=nlogaM,
(a∈R+,m,n∈R)(M,N∈R+,a>0,a≠1).
2.指数函数、对数函数
(1)要熟记这二个函数在不同条件下的图象,并能熟练地由图象“读”出该函数的主要性质;
(2)同底数的指数函数和对数函数的图象关于直线y=x成轴对称图形。由图可“读”出指数函数和对数函数的主要性质:
指数函数
对数函数
(1)定义域:R
(1)定义域:R+
(2)值域:R+
(2)值域:R
(3)过点(0,1)
(3)过点(1,0)
(4)a>1时为增函数,
0<a<1时为减函数。
(4)a>1时为增函数,
0<a<1时为减函数。
如果两个函数y=f(x)和x=g(y)描述的是同一个对应法则,则称这两个函数互为反函数.这时两者之间满足关系g(f(x))=x和f(g(y))=y,并且它们的图象关于直线y=x成轴对称.函数f叫作g的反函数,g也叫作f的反函数.f的定义域是g的值域,f的值域是g的定义域,两者同为递增或递减。
由上面反函数的定义,我们知道,指数函数y=ax(a>0且a≠1)和同底数的对数函数y=logax(a>0且a≠1)互为反函数。这给研究对数函数的图象和性质带来了方便。
4.函数模型及其应用
(1)目前我们能建立的函数模型主要是一次函数,二次函数,幂函数,指数函数和对数函数的模型;
(2)建模的目的是:模拟实际问题和用模拟函数的性质去推测判断未进行测量或不便测量的数据,特别是实际问题的未来走势;
(3)建模的大致步骤是:了解和简化实际问题,建立实际问题的数学模型,分析所得数学模型,把模型所判断的结论和实际模型的表现加以比较,改进数学模型。
题型一 有关指数、对数的运算问题
指数与指数运算、对数与对数运算是两个重要的知识点,不仅是本章考查的重要题型,也是高考的必考内容。
指数式的运算首先要注意化简顺序,一般负指数先转化成正指数,根式化为指数式;其次若出现分式,则要注意把分子、分母因式分解以达到约分的目的对数运算首先要注意公式应用过程中范围的变化,前后要等价;其次要熟练地运用对数的三个运算性质,并根据具体问题合理利用对数恒等式和换底公式等。换底公式是对数计算、化简、证明常用的公式,一定要掌握并灵活运用。
题型研修
=log39-9=2-9=-7.
题型二 指数函数、对数函数及幂函数的图象与性质
函数的图象是研究函数性质的前提和基础,它较形象直观地反映了函数的一切性质。教材对幂、指、对三个函数的性质的研究也正好体现了由图象到性质,由具体到抽象的过程,突出了函数图象在研究相应函数性质时的作用。
例2 已知函数f(x)是定义在R上的偶函数,当x≥0时,
(1)画出函数f(x)的图象;
解 先作出当x≥0时,f(x)=
x的图象,利用偶函数的图象关于y轴对称,再作出f(x)在x∈(-∞,0)时的图象.
(2)根据图象写出f(x)的单调区间,并写出函数的值域。
解 函数f(x)的单调递增区间为(-∞,0),
单调递减区间为[0,+∞),值域为(0,1].
跟踪演练2 (1)函数f(x)=ln
x的图象与函数g(x)=x2-4x+4的图象的交点个数为( )
A.0
B.1
C.2
D.3
解析 作出两个函数的图象,利用数形结合思想求解。
g(x)=x2-4x+4=(x-2)2,在同一平面
直角坐标系内画出函数f(x)=ln
x与
g(x)=(x-2)2的图象(如图),
由图可得两个函数的图象有2个交点。
C
解析 由3x-1≠0得x≠0,
但从选项D的函数图象可以看出函数在(0,+∞)上是单调递增函数,两者矛盾,可排除选项D,故选C。
答案 C
题型三 比较大小
比较几个数的大小问题是指数函数、对数函数和幂函数的重要应用,其基本方法是:将需要比较大小的几个数视为某类函数的函数值,其主要方法可分以下三种:
(1)根据函数的单调性(如根据一次函数、二次函数、指数函数、对数函数、幂函数的单调性),利用单调性的定义求解;
(2)采用中间量的方法(实际上也要用到函数的单调性),常用的中间量如0,1,-1等;
(3)采用数形结合的方法,通过函数的图象解决。
A.a<b<c
B.c<b<a
C.c<a<b
D.b<a<c
故有a<b<c.
A
跟踪演练3 (1)下列不等式成立的是( )
A.log32<log23<log25
B.log32<log25<log23
C.log23<log32<log25
D.log23<log25<log32
解析 由于log31<log32<log33,
log22<log23<log25,
即0<log32<1,1<log23<log25,
所以log32<log23<log25.故选A.
A
A.x>y>z
B.z>y>x
C.y>x>z
D.z>x>y
C
题型四 简单指数方程和对数方程的解法
通过理解指数方程、对数方程的概念,灵活运用指数函数与对数函数的性质,对简单的指数方程和对数方程进行求解,解决一些简单的实际问题。
A.1
B.9
C.25
D.125
D
题型五 分类讨论思想
本章常见分类讨论思想的应用如下表:
问题
讨论标准
分类情况
比较af(x)与ag(x)的大小
a与1的大小关系
(1)a>1时,若f(x)>g(x),则af(x)>ag(x);
(2)0<a<1时,若f(x)>g(x),则af(x)<ag(x).
解不等式af(x)>ag(x)
a与1的大小关系
(1)a>1时,f(x)>g(x);
(2)0<a<1时,f(x)<g(x).
比较logax1与logax2的大小
a与1的大小关系
(1)a>1时,若x1>x2,则logax1>logax2;
(2)0<a<1时,若x1>x2,则logax1<logax2.
解不等式logaf(x)>logag(x)
a与1的大小关系
(1)a>1时,f(x)>g(x)>0;
(2)0<a<1时,0<f(x)<g(x).
例5 已知偶函数f(x)在x∈[0,+∞)上是增函数,f
=0,求不等式f(logax)>0(a>0,且a≠1)的解集.
解 ∵f(x)是偶函数,且f(x)在[0,+∞)上是增函数,
题型六 函数的实际应用问题
利用给定的函数模型或建立确定的函数模型解决实际问题的方法:
(1)根据题意选用恰当的函数模型来描述所涉及的数量之间的关系;
(2)利用待定系数法,确定具体函数模型;
(3)对所选定的函数模型进行适当的评价、比较,并选择最恰当的模型;
(4)根据实际问题对模型进行适当的修正。
题型六 函数的实际应用问题
例6
某跨国饮料公司在对全世界所有人均GDP(即人均纯收入)在0.5千美元~8千美元的地区销售该公司A饮料的情况的调查中发现:人均GDP处在中等的地区对该饮料的销售量最多,然后向两边递减.
(1)下列几个模拟函数中(x表示人均GDP,单位:千美元,y表示A饮料的年人均销量,单位:升),用哪个模拟函数来描述A饮料的年人均销量与地区的人均GDP关系更合适 说明理由.y=ax2+bx,y=kx+b,y=logax+b,y=ax+b.
解
(1)用函数y=ax2+bx来描述A饮料的年人均销量与地区的人均GDP的关
系更合适。因为函数y=kx+b,y=logax+b,y=ax+b在其定义域内都是单调函数,不具备先递增后递减的特征。
(2)若人均GDP为1千美元时,A饮料的年人均销量为2升;若人均GDP为4千美元时,A饮料的年人均销量为5升,把(1)中你所选的模拟函数求出来,并求出各个地区中,A饮料的年人均销量最多是多少
课堂小结
1.函数是高中数学极为重要的内容,函数思想和函数方法贯穿高中数学的整个过程,纵观历年高考试题,对本章的考查是以基本函数形式出现的综合题和应用题,一直是常考不衰的热点问题。
2.从考查角度看,指数函数、对数函数概念的考查以基本概念与基本计算为主;对图象的考查重在考查平移变换、对称变换以及利用数形结合的思想方法解决数学问题的能力;对幂函数的考查将会从概念、图象、性质等方面来考查。
3.对于简单的指数方程和对数方程,借助两者函数的性质可进行计算求解。
4.函数模型的应用实例的基本题型:
(1)给定函数模型解决实际问题;
(2)建立确定性的函数模型解决问题;
(3)建立拟合函数模型解决实际问题。
谢
谢
