沪教版(上海)高中数学高一下册 5.1 三角比 复习课件(共22张PPT)
文档属性
| 名称 | 沪教版(上海)高中数学高一下册 5.1 三角比 复习课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 00:00:00 | ||
图片预览


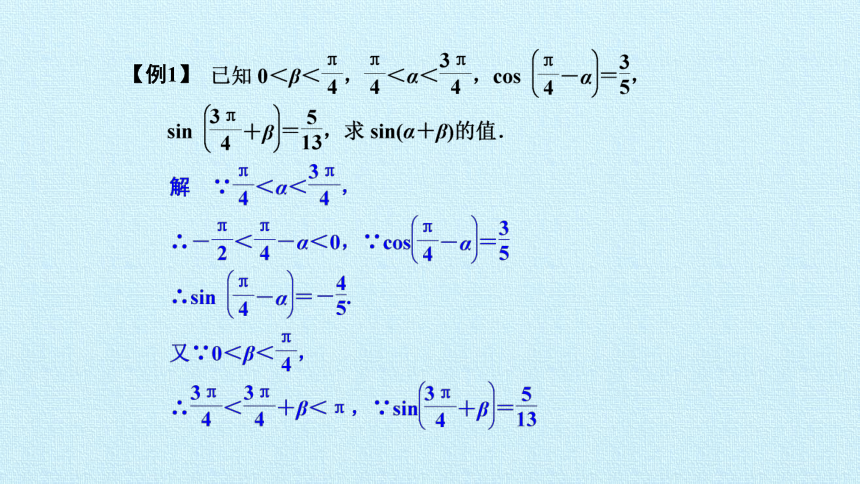

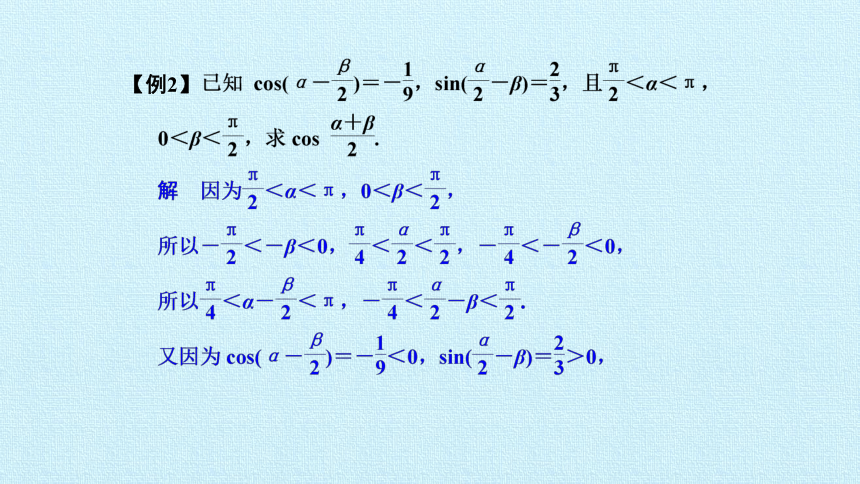


文档简介
(共22张PPT)
第5章
三角比
复习课件
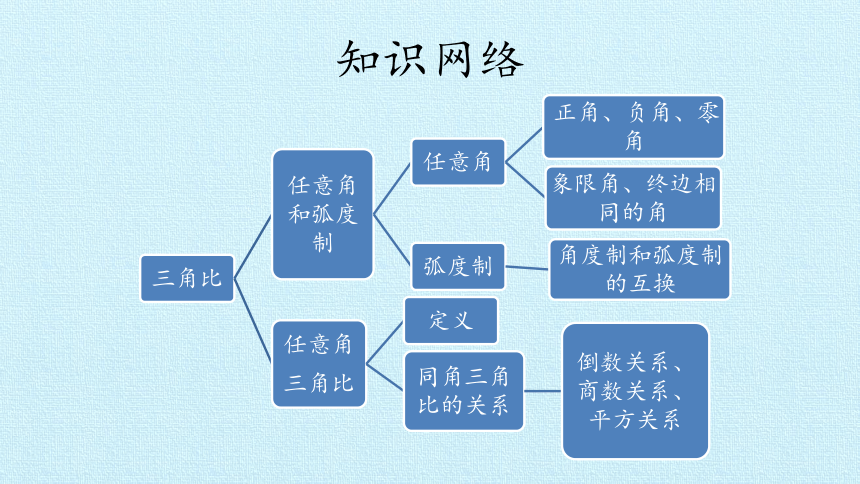
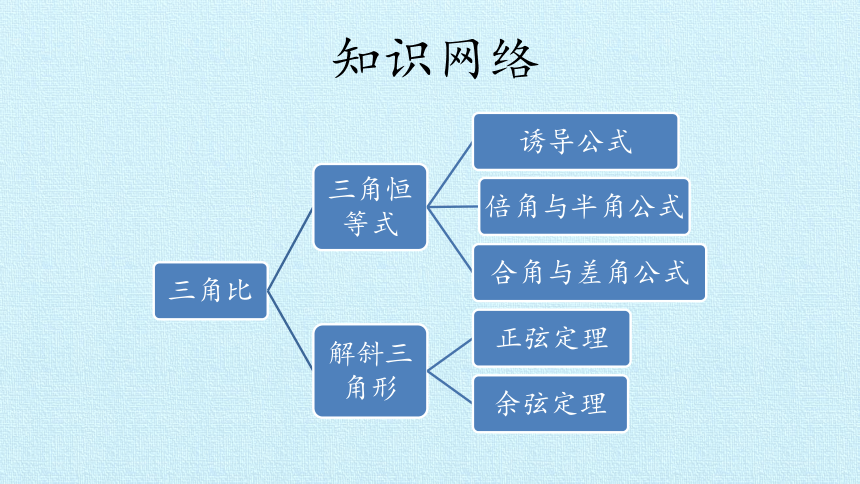
知识网络
知识网络
专题一
三角变换中的求值问题
三角变换中的求值问题主要有两类,给角求值和给值求值。
给角求值一般是利用和、差、倍公式进行变换,使其出现特殊角,若为非特殊角,则应变为可消去或约分的情况,从而求出其值。
给值求值一般应先化简所求的式子,弄清实际所求,或变化已知的式子,寻找已知与所求的联系,再求值。
【例1】
点评 由于已知条件中的角与所求式中的角度不一致,将它们统一起来再变换是解题的关键。
【例2】
三角恒等式的证明主要有两种类型:绝对恒等式与条件恒等式。
证明绝对恒等式要根据等式两边的特征,采取化繁为简,左右归一,变更命题等方法,通过三角恒等变换,使等式的两边化异为同。
条件恒等式的证明则要认真观察、比较已知条件与求证等式之间的联系,选择适当途径。常用代入法、消去法、两头凑等。
专题二
三角恒等式的证明
已知tan(α+β)=2tan
β,求证:3sin
α=sin(α+2β).
【例3】
∴sin(α+β)·cos
β=2cos(α+β)·sin
β.
而sin(α+2β)=sin
[(α+β)+β]
=sin(α+β)·cos
β+cos(α+β)·sin
β
=2cos(α+β)·sin
β+cos(α+β)·sin
β
=3cos(α+β)·sin
β.
又sin
α=sin
[(α+β)-β]
=sin(α+β)·cos
β-cos(α+β)·sin
β
=2cos(α+β)·sin
β-cos(α+β)·sin
β
=cos(α+β)·sin
β.
故sin(α+2β)=3sin
α.
点评 三角式的化简或证明,主要从三方面寻求思路:一是观察函数特点,已知和所求中包含什么函数,它们可以怎样联系;二是观察角的特点,它们之间可经过何种形式联系起来;三是观察结构特点,它们之间经过怎样的变形可达到统一。
【例4】
【例5】
专题三
三角变换的综合应用
点评 三角形中的问题注意补角关系(A+B+C=π)和余角关系
等三角形的有关知识的运用。
(1)若锐角△ABC的面积为
,且AB=5,AC=8,则BC=
.
7
专题四
正余弦定理在解三角形中的应用
【例6】
【例7】
点评 利用正弦、余弦定理寻求三角形各元素之间的关系来解决三角形及其面积问题。
检测题
1.已知角α的终边经过点P(1,
),则cos
2α的值为( )
A.
B.
C.
D.
答案:A
解析:依题意知
,
所以cos
2α=2cos2α-1=2
-1=
.
2.设θ∈
,
,则cos
θ-sin
θ的值是( )
A.
B.
C.
D.
答案:D
解析:由
,得sin
2θ=
,
于是(cos
θ-sin
θ)2=1-sin
2θ=
,
而θ∈
,
所以cos
θ<sin
θ,于是cos
θ-sin
θ=
.
3.若
,则
等于( )
A.
B.
C.
D.
答案:A
解析:由于
,
所以
,
于是
=
-1=2
-1=
.
4.已知锐角△ABC的面积为3,BC=4,
CA=3,则角C
的大小为(
)
A.75°
B.60°
C.45°
D.30°
∵三角形为锐角三角形.
∴C=30°.
答案:D
谢
谢
第5章
三角比
复习课件
知识网络
知识网络
专题一
三角变换中的求值问题
三角变换中的求值问题主要有两类,给角求值和给值求值。
给角求值一般是利用和、差、倍公式进行变换,使其出现特殊角,若为非特殊角,则应变为可消去或约分的情况,从而求出其值。
给值求值一般应先化简所求的式子,弄清实际所求,或变化已知的式子,寻找已知与所求的联系,再求值。
【例1】
点评 由于已知条件中的角与所求式中的角度不一致,将它们统一起来再变换是解题的关键。
【例2】
三角恒等式的证明主要有两种类型:绝对恒等式与条件恒等式。
证明绝对恒等式要根据等式两边的特征,采取化繁为简,左右归一,变更命题等方法,通过三角恒等变换,使等式的两边化异为同。
条件恒等式的证明则要认真观察、比较已知条件与求证等式之间的联系,选择适当途径。常用代入法、消去法、两头凑等。
专题二
三角恒等式的证明
已知tan(α+β)=2tan
β,求证:3sin
α=sin(α+2β).
【例3】
∴sin(α+β)·cos
β=2cos(α+β)·sin
β.
而sin(α+2β)=sin
[(α+β)+β]
=sin(α+β)·cos
β+cos(α+β)·sin
β
=2cos(α+β)·sin
β+cos(α+β)·sin
β
=3cos(α+β)·sin
β.
又sin
α=sin
[(α+β)-β]
=sin(α+β)·cos
β-cos(α+β)·sin
β
=2cos(α+β)·sin
β-cos(α+β)·sin
β
=cos(α+β)·sin
β.
故sin(α+2β)=3sin
α.
点评 三角式的化简或证明,主要从三方面寻求思路:一是观察函数特点,已知和所求中包含什么函数,它们可以怎样联系;二是观察角的特点,它们之间可经过何种形式联系起来;三是观察结构特点,它们之间经过怎样的变形可达到统一。
【例4】
【例5】
专题三
三角变换的综合应用
点评 三角形中的问题注意补角关系(A+B+C=π)和余角关系
等三角形的有关知识的运用。
(1)若锐角△ABC的面积为
,且AB=5,AC=8,则BC=
.
7
专题四
正余弦定理在解三角形中的应用
【例6】
【例7】
点评 利用正弦、余弦定理寻求三角形各元素之间的关系来解决三角形及其面积问题。
检测题
1.已知角α的终边经过点P(1,
),则cos
2α的值为( )
A.
B.
C.
D.
答案:A
解析:依题意知
,
所以cos
2α=2cos2α-1=2
-1=
.
2.设θ∈
,
,则cos
θ-sin
θ的值是( )
A.
B.
C.
D.
答案:D
解析:由
,得sin
2θ=
,
于是(cos
θ-sin
θ)2=1-sin
2θ=
,
而θ∈
,
所以cos
θ<sin
θ,于是cos
θ-sin
θ=
.
3.若
,则
等于( )
A.
B.
C.
D.
答案:A
解析:由于
,
所以
,
于是
=
-1=2
-1=
.
4.已知锐角△ABC的面积为3,BC=4,
CA=3,则角C
的大小为(
)
A.75°
B.60°
C.45°
D.30°
∵三角形为锐角三角形.
∴C=30°.
答案:D
谢
谢
