2021-2022学年人教版七年级上 4.1 几何图形同步练习(含解析)
文档属性
| 名称 | 2021-2022学年人教版七年级上 4.1 几何图形同步练习(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 10:38:10 | ||
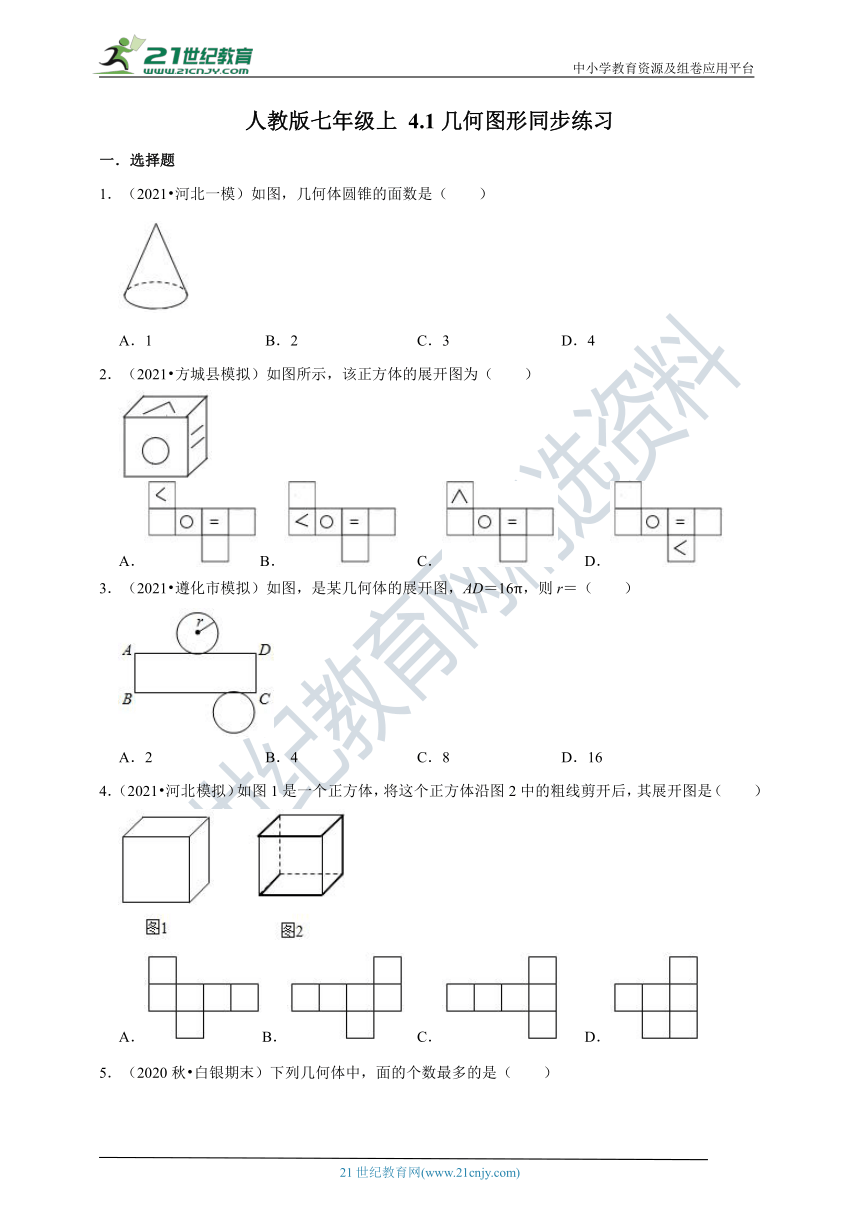
图片预览

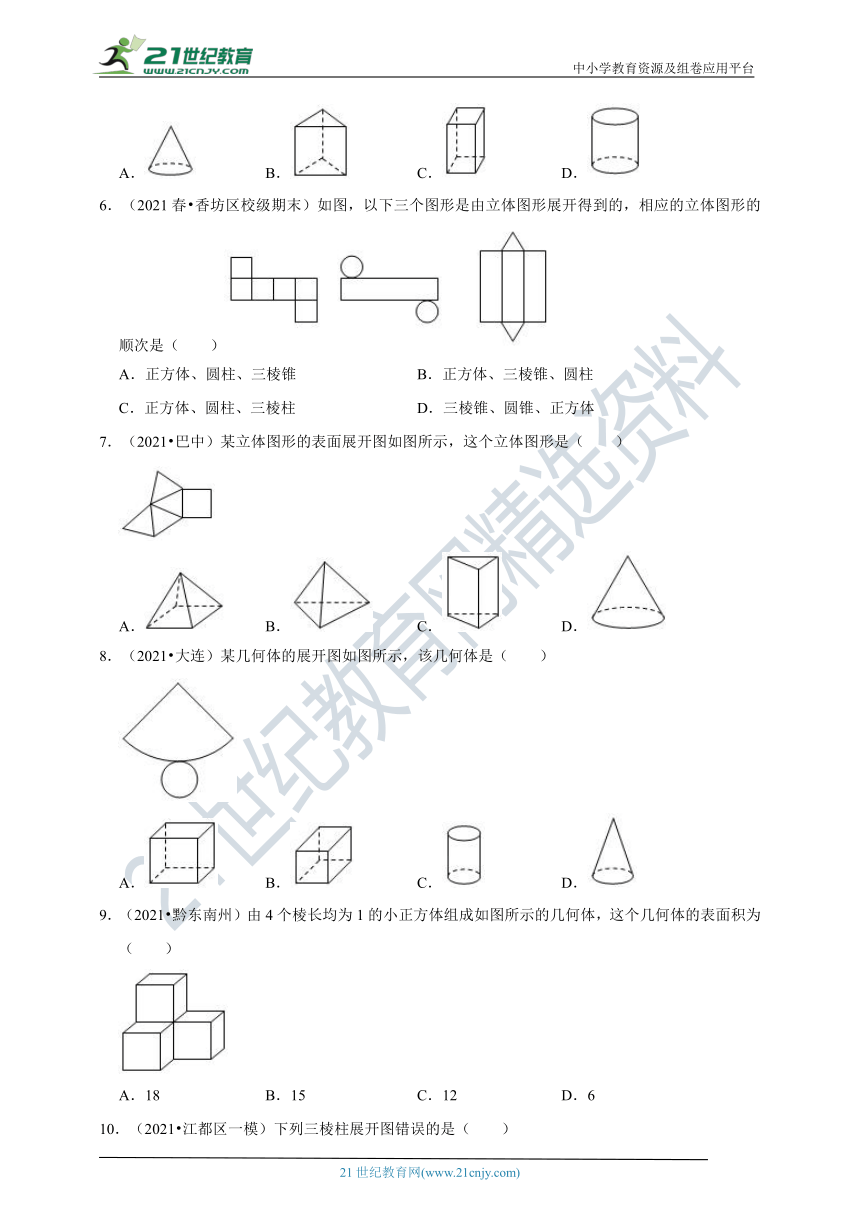



文档简介
中小学教育资源及组卷应用平台
人教版七年级上
4.1几何图形同步练习
一.选择题
1.(2021 河北一模)如图,几何体圆锥的面数是( )
A.1
B.2
C.3
D.4
2.(2021 方城县模拟)如图所示,该正方体的展开图为( )
A.B.
C.
D.
3.(2021 遵化市模拟)如图,是某几何体的展开图,AD=16π,则r=( )
A.2
B.4
C.8
D.16
4.(2021 河北模拟)如图1是一个正方体,将这个正方体沿图2中的粗线剪开后,其展开图是( )
A.B.
C.
D.
5.(2020秋 白银期末)下列几何体中,面的个数最多的是( )
A.
B.
C.
D.
6.(2021春 香坊区校级期末)如图,以下三个图形是由立体图形展开得到的,相应的立体图形的顺次是( )
A.正方体、圆柱、三棱锥
B.正方体、三棱锥、圆柱
C.正方体、圆柱、三棱柱
D.三棱锥、圆锥、正方体
7.(2021 巴中)某立体图形的表面展开图如图所示,这个立体图形是( )
A.
B.
C.
D.
8.(2021 大连)某几何体的展开图如图所示,该几何体是( )
A.
B.
C.
D.
9.(2021 黔东南州)由4个棱长均为1的小正方体组成如图所示的几何体,这个几何体的表面积为( )
A.18
B.15
C.12
D.6
10.(2021 江都区一模)下列三棱柱展开图错误的是( )
A.
B.
C.
D.
11.(2021 贵阳)下列几何体中,圆柱体是( )
A.
B.
C.
D.
12.(2021 怀化)下列图形中,可能是圆锥侧面展开图的是( )
A.
B.
C.
D.
二.填空题
13.(2021 锦江区校级开学)如图是某包装盒的表面展开图,这个几何体的表面积是
.
14.(2020秋 新都区校级期末)在一个棱柱中,一共有5个面,则这个棱柱有
条棱,有
个顶点.
15.(2021 永州模拟)有一个正六面体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动90°算一次,则滚动第2021次后,骰子朝下一面的点数是
.
16.(2021 龙港区一模)如图是某个几何体的展开图,该几何体是
.
17.(2020秋 武侯区期末)如图是一个正方体的表面展开图,若正方体中相对的面的数互为相反数,则x+y的值为
.
三.解答题
18.(2020秋 神木市期末)如图是一个正方体的表面展开图,如果正方体相对面上所标的两个数互为相反数.
(1)判断x、y、z所在的面分别与哪个数字所在的面是相对面;
(2)求x﹣2y﹣3z的值.
19.(2020秋 河西区期末)如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.
20.(2020秋 中原区校级月考)已知长方形的长为5cm,宽为4cm,将其绕它的一边所在的直线旋转一周,得到一个立体图形.
(1)得到的几何图形的名称为
,这个现象用数学知识解释为
.
(2)求此几何体的表面积;(结果保留π)
(3)求此几何体的体积.(结果保留π)
21.(2020秋 铁岭月考)如图所示是长方体的表面展开图,折叠成一个长方体,那么:
(1)与N重合的点是哪几个?
(2)若AE=FH=14cm,FG=2cm,则该长方体的表面积和体积分别是多少?
参考答案与试题解析
一.选择题
1.(2021 河北一模)如图,几何体圆锥的面数是( )
A.1
B.2
C.3
D.4
【解析】解:圆锥体是由一个底面和一个侧面围成的,
故选:B.
2.(2021 方城县模拟)如图所示,该正方体的展开图为( )
A.B.
C.
D.
【解析】解:根据正方体表面展开图的“相对的面”的判断方法可知,
选项B中面“<”与“=”是对面,因此选项B不符合题意;
再根据上面“∧”符号开口,可以判断选项A符合题意;选项C、D不符合题意;
故选:A.
3.(2021 遵化市模拟)如图,是某几何体的展开图,AD=16π,则r=( )
A.2
B.4
C.8
D.16
【解析】解:由图可知,该几何体是圆柱,
∵AD=16π,
∴底面圆的圆周长是16π,
故2πr=16π,解得r=8.
故选:C.
4.(2021 河北模拟)如图1是一个正方体,将这个正方体沿图2中的粗线剪开后,其展开图是( )
A.B.
C.
D.
【解析】解:如图1的正方体沿图2中的粗线剪开后,其展开图是:
故选:C.
5.(2020秋 白银期末)下列几何体中,面的个数最多的是( )
A.
B.
C.
D.
【解析】解:A选项有一个底面一个侧面,共两个面;
B选项有两个底面三个侧面,共五个面;
C选项有两个底面四个侧面,共六个面;
D选项有两个底面一个侧面,共三个面;
故选:C.
6.(2021春 香坊区校级期末)如图,以下三个图形是由立体图形展开得到的,相应的立体图形的顺次是( )
A.正方体、圆柱、三棱锥
B.正方体、三棱锥、圆柱
C.正方体、圆柱、三棱柱
D.三棱锥、圆锥、正方体
【解析】解:观察图形,由立体图形及其表面展开图的特点可知相应的立体图形顺次是正方体、圆柱、三棱柱.
故选:C.
7.(2021 巴中)某立体图形的表面展开图如图所示,这个立体图形是( )
A.
B.
C.
D.
【解析】解:四个三角形和一个四边形,是四棱锥的组成,所以该立体图形的名称为四棱锥.
故选:A.
8.(2021 大连)某几何体的展开图如图所示,该几何体是( )
A.
B.
C.
D.
【解析】解:扇形和圆折叠后,能围成的几何体是圆锥.
故选:D.
9.(2021 黔东南州)由4个棱长均为1的小正方体组成如图所示的几何体,这个几何体的表面积为( )
A.18
B.15
C.12
D.6
【解析】解:正视图中正方形有3个;
左视图中正方形有3个;
俯视图中正方形有3个.
则这个几何体表面正方形的个数是:2×(3+3+3)=18.
则几何体的表面积为18.
故选:A.
10.(2021 江都区一模)下列三棱柱展开图错误的是( )
A.B.C.
D.
【解析】解:A、B、C中间三个长方形能围成三棱柱的侧面,上、下两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.D围成三棱柱时,两个三角形重合为同一底面,而另一底面没有.故D不能围成三棱柱.
故选:D.
11.(2021 贵阳)下列几何体中,圆柱体是( )
A.
B.
C.
D.
【解析】解:A、这个几何体是圆锥,故本选项不符合题意;
B、这个几何体是圆台,故本选项不符合题意;
C、这个几何体是圆柱,故本选项符合题意;
D、这个几何体是棱台,故本选项不符合题意.
故选:C.
12.(2021 怀化)下列图形中,可能是圆锥侧面展开图的是( )
A.B.
C.
D.
【解析】解:圆锥的侧面展开图是扇形,
故选:B.
二.填空题
13.(2021 锦江区校级开学)如图是某包装盒的表面展开图,这个几何体的表面积是
250π .
【解析】解:由图形可知:圆柱的底面半径r=5,h=20,
S=2πr2+2πrh=2π 52+2π 5 20=50π+200π=250π.
故答案为:250π.
14.(2020秋 新都区校级期末)在一个棱柱中,一共有5个面,则这个棱柱有
9 条棱,有
6 个顶点.
【解析】解:一个棱柱中,一共有5个面,则有2个底面,3个侧面,因此此立体图形是三棱柱,则这个棱柱棱的条数有9条,有6个顶点.
故答案为:9;6.
15.(2021 永州模拟)有一个正六面体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动90°算一次,则滚动第2021次后,骰子朝下一面的点数是 2 .
【解析】解:观察图形知道点数三和点数四相对,点数二和点数五相对且滚动四次一循环,
∵2021÷4=505…1,
∴滚动第2021次后与第1次相同,
∴朝下的数字是5的对面2,
故答案为:2.
16.(2021 龙港区一模)如图是某个几何体的展开图,该几何体是 三棱柱 .
【解析】解:由展开图可得,该几何体有三个面是长方形,两个面是三角形,
∴该几何体为三棱柱,
故答案为:三棱柱.
17.(2020秋 武侯区期末)如图是一个正方体的表面展开图,若正方体中相对的面的数互为相反数,则x+y的值为 ﹣8 .
【解析】解:正方体的表面展开图,相对的面之间一定相隔一个正方形.
“y”与“|﹣5|”是相对面,
“﹣22”与“1﹣x”是相对面,
“﹣2”与“3”是相对面,
∵相对的面上的数字互为相反数,
∴y=﹣5,x=﹣3,
∴x+y=﹣5﹣3=﹣8.
故答案为:﹣8.
三.解答题
18.(2020秋 神木市期末)如图是一个正方体的表面展开图,如果正方体相对面上所标的两个数互为相反数.
(1)判断x、y、z所在的面分别与哪个数字所在的面是相对面;
(2)求x﹣2y﹣3z的值.
【解析】解:(1)由正方体的表面展开图的“相间、Z端是对面”可知,
“﹣8”与“x”是对面,
“y”与“﹣2”是对面,
“3”与“z”是对面,
(2)由于正方体相对面上所标的两个数互为相反数.
所以x=8,y=2,z=﹣3,
所以x﹣2y﹣3z=8﹣2×2﹣3×(﹣3)=8﹣4+9=13,
答:x﹣2y﹣3z的值为13.
19.(2020秋 河西区期末)如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.
【解析】解:由简单几何体的展开与折叠可得,
20.(2020秋 中原区校级月考)已知长方形的长为5cm,宽为4cm,将其绕它的一边所在的直线旋转一周,得到一个立体图形.
(1)得到的几何图形的名称为
圆柱 ,这个现象用数学知识解释为
面动成体 .
(2)求此几何体的表面积;(结果保留π)
(3)求此几何体的体积.(结果保留π)
【解析】解:(1)长方形绕一边旋转一周,得圆柱,
这个现象用数学知识解释为面动成体,
故答案为:圆柱,面动成体;
(2)①以长方形的长为轴旋转,则圆柱的底面半径r=4cm,
∴圆柱的表面积为:2πrl+2πr2=2π×4×5+2π×42=72π
(cm2);
②以长方形的宽为轴旋转,则圆柱的底面半径r=5cm,
∴圆柱的表面积为:2πrl+2πr2=2π×5×4+2π×52=90π
(cm2).
∴圆柱的表面积为72πcm2或90πcm2;
(3)分(2)中两种情况:
①圆柱的体积为V=πr2l=π×42×5=80π(
cm3);
②圆柱的体积为V=πr2l=π×52×4=100π
(cm3).
∴圆柱的体积为80πcm3或100πcm3.
21.(2020秋 铁岭月考)如图所示是长方体的表面展开图,折叠成一个长方体,那么:
(1)与N重合的点是哪几个?
(2)若AE=FH=14cm,FG=2cm,则该长方体的表面积和体积分别是多少?
【解析】(1)与N重合的点有点H和点J.
(2)有长方体展开图可知:FG=AB=CD=2cm,
∴AF=BC=DE=(14﹣2×2)÷2=5cm,
∴AH=FH﹣AF=14﹣5=9cm,
∴S=14×9+2×2×5=146cm2,
∴V=2×5×9=90cm3,
答:该长方体的表面积和体积分别为146cm2和90cm3.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
人教版七年级上
4.1几何图形同步练习
一.选择题
1.(2021 河北一模)如图,几何体圆锥的面数是( )
A.1
B.2
C.3
D.4
2.(2021 方城县模拟)如图所示,该正方体的展开图为( )
A.B.
C.
D.
3.(2021 遵化市模拟)如图,是某几何体的展开图,AD=16π,则r=( )
A.2
B.4
C.8
D.16
4.(2021 河北模拟)如图1是一个正方体,将这个正方体沿图2中的粗线剪开后,其展开图是( )
A.B.
C.
D.
5.(2020秋 白银期末)下列几何体中,面的个数最多的是( )
A.
B.
C.
D.
6.(2021春 香坊区校级期末)如图,以下三个图形是由立体图形展开得到的,相应的立体图形的顺次是( )
A.正方体、圆柱、三棱锥
B.正方体、三棱锥、圆柱
C.正方体、圆柱、三棱柱
D.三棱锥、圆锥、正方体
7.(2021 巴中)某立体图形的表面展开图如图所示,这个立体图形是( )
A.
B.
C.
D.
8.(2021 大连)某几何体的展开图如图所示,该几何体是( )
A.
B.
C.
D.
9.(2021 黔东南州)由4个棱长均为1的小正方体组成如图所示的几何体,这个几何体的表面积为( )
A.18
B.15
C.12
D.6
10.(2021 江都区一模)下列三棱柱展开图错误的是( )
A.
B.
C.
D.
11.(2021 贵阳)下列几何体中,圆柱体是( )
A.
B.
C.
D.
12.(2021 怀化)下列图形中,可能是圆锥侧面展开图的是( )
A.
B.
C.
D.
二.填空题
13.(2021 锦江区校级开学)如图是某包装盒的表面展开图,这个几何体的表面积是
.
14.(2020秋 新都区校级期末)在一个棱柱中,一共有5个面,则这个棱柱有
条棱,有
个顶点.
15.(2021 永州模拟)有一个正六面体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动90°算一次,则滚动第2021次后,骰子朝下一面的点数是
.
16.(2021 龙港区一模)如图是某个几何体的展开图,该几何体是
.
17.(2020秋 武侯区期末)如图是一个正方体的表面展开图,若正方体中相对的面的数互为相反数,则x+y的值为
.
三.解答题
18.(2020秋 神木市期末)如图是一个正方体的表面展开图,如果正方体相对面上所标的两个数互为相反数.
(1)判断x、y、z所在的面分别与哪个数字所在的面是相对面;
(2)求x﹣2y﹣3z的值.
19.(2020秋 河西区期末)如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.
20.(2020秋 中原区校级月考)已知长方形的长为5cm,宽为4cm,将其绕它的一边所在的直线旋转一周,得到一个立体图形.
(1)得到的几何图形的名称为
,这个现象用数学知识解释为
.
(2)求此几何体的表面积;(结果保留π)
(3)求此几何体的体积.(结果保留π)
21.(2020秋 铁岭月考)如图所示是长方体的表面展开图,折叠成一个长方体,那么:
(1)与N重合的点是哪几个?
(2)若AE=FH=14cm,FG=2cm,则该长方体的表面积和体积分别是多少?
参考答案与试题解析
一.选择题
1.(2021 河北一模)如图,几何体圆锥的面数是( )
A.1
B.2
C.3
D.4
【解析】解:圆锥体是由一个底面和一个侧面围成的,
故选:B.
2.(2021 方城县模拟)如图所示,该正方体的展开图为( )
A.B.
C.
D.
【解析】解:根据正方体表面展开图的“相对的面”的判断方法可知,
选项B中面“<”与“=”是对面,因此选项B不符合题意;
再根据上面“∧”符号开口,可以判断选项A符合题意;选项C、D不符合题意;
故选:A.
3.(2021 遵化市模拟)如图,是某几何体的展开图,AD=16π,则r=( )
A.2
B.4
C.8
D.16
【解析】解:由图可知,该几何体是圆柱,
∵AD=16π,
∴底面圆的圆周长是16π,
故2πr=16π,解得r=8.
故选:C.
4.(2021 河北模拟)如图1是一个正方体,将这个正方体沿图2中的粗线剪开后,其展开图是( )
A.B.
C.
D.
【解析】解:如图1的正方体沿图2中的粗线剪开后,其展开图是:
故选:C.
5.(2020秋 白银期末)下列几何体中,面的个数最多的是( )
A.
B.
C.
D.
【解析】解:A选项有一个底面一个侧面,共两个面;
B选项有两个底面三个侧面,共五个面;
C选项有两个底面四个侧面,共六个面;
D选项有两个底面一个侧面,共三个面;
故选:C.
6.(2021春 香坊区校级期末)如图,以下三个图形是由立体图形展开得到的,相应的立体图形的顺次是( )
A.正方体、圆柱、三棱锥
B.正方体、三棱锥、圆柱
C.正方体、圆柱、三棱柱
D.三棱锥、圆锥、正方体
【解析】解:观察图形,由立体图形及其表面展开图的特点可知相应的立体图形顺次是正方体、圆柱、三棱柱.
故选:C.
7.(2021 巴中)某立体图形的表面展开图如图所示,这个立体图形是( )
A.
B.
C.
D.
【解析】解:四个三角形和一个四边形,是四棱锥的组成,所以该立体图形的名称为四棱锥.
故选:A.
8.(2021 大连)某几何体的展开图如图所示,该几何体是( )
A.
B.
C.
D.
【解析】解:扇形和圆折叠后,能围成的几何体是圆锥.
故选:D.
9.(2021 黔东南州)由4个棱长均为1的小正方体组成如图所示的几何体,这个几何体的表面积为( )
A.18
B.15
C.12
D.6
【解析】解:正视图中正方形有3个;
左视图中正方形有3个;
俯视图中正方形有3个.
则这个几何体表面正方形的个数是:2×(3+3+3)=18.
则几何体的表面积为18.
故选:A.
10.(2021 江都区一模)下列三棱柱展开图错误的是( )
A.B.C.
D.
【解析】解:A、B、C中间三个长方形能围成三棱柱的侧面,上、下两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.D围成三棱柱时,两个三角形重合为同一底面,而另一底面没有.故D不能围成三棱柱.
故选:D.
11.(2021 贵阳)下列几何体中,圆柱体是( )
A.
B.
C.
D.
【解析】解:A、这个几何体是圆锥,故本选项不符合题意;
B、这个几何体是圆台,故本选项不符合题意;
C、这个几何体是圆柱,故本选项符合题意;
D、这个几何体是棱台,故本选项不符合题意.
故选:C.
12.(2021 怀化)下列图形中,可能是圆锥侧面展开图的是( )
A.B.
C.
D.
【解析】解:圆锥的侧面展开图是扇形,
故选:B.
二.填空题
13.(2021 锦江区校级开学)如图是某包装盒的表面展开图,这个几何体的表面积是
250π .
【解析】解:由图形可知:圆柱的底面半径r=5,h=20,
S=2πr2+2πrh=2π 52+2π 5 20=50π+200π=250π.
故答案为:250π.
14.(2020秋 新都区校级期末)在一个棱柱中,一共有5个面,则这个棱柱有
9 条棱,有
6 个顶点.
【解析】解:一个棱柱中,一共有5个面,则有2个底面,3个侧面,因此此立体图形是三棱柱,则这个棱柱棱的条数有9条,有6个顶点.
故答案为:9;6.
15.(2021 永州模拟)有一个正六面体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动90°算一次,则滚动第2021次后,骰子朝下一面的点数是 2 .
【解析】解:观察图形知道点数三和点数四相对,点数二和点数五相对且滚动四次一循环,
∵2021÷4=505…1,
∴滚动第2021次后与第1次相同,
∴朝下的数字是5的对面2,
故答案为:2.
16.(2021 龙港区一模)如图是某个几何体的展开图,该几何体是 三棱柱 .
【解析】解:由展开图可得,该几何体有三个面是长方形,两个面是三角形,
∴该几何体为三棱柱,
故答案为:三棱柱.
17.(2020秋 武侯区期末)如图是一个正方体的表面展开图,若正方体中相对的面的数互为相反数,则x+y的值为 ﹣8 .
【解析】解:正方体的表面展开图,相对的面之间一定相隔一个正方形.
“y”与“|﹣5|”是相对面,
“﹣22”与“1﹣x”是相对面,
“﹣2”与“3”是相对面,
∵相对的面上的数字互为相反数,
∴y=﹣5,x=﹣3,
∴x+y=﹣5﹣3=﹣8.
故答案为:﹣8.
三.解答题
18.(2020秋 神木市期末)如图是一个正方体的表面展开图,如果正方体相对面上所标的两个数互为相反数.
(1)判断x、y、z所在的面分别与哪个数字所在的面是相对面;
(2)求x﹣2y﹣3z的值.
【解析】解:(1)由正方体的表面展开图的“相间、Z端是对面”可知,
“﹣8”与“x”是对面,
“y”与“﹣2”是对面,
“3”与“z”是对面,
(2)由于正方体相对面上所标的两个数互为相反数.
所以x=8,y=2,z=﹣3,
所以x﹣2y﹣3z=8﹣2×2﹣3×(﹣3)=8﹣4+9=13,
答:x﹣2y﹣3z的值为13.
19.(2020秋 河西区期末)如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.
【解析】解:由简单几何体的展开与折叠可得,
20.(2020秋 中原区校级月考)已知长方形的长为5cm,宽为4cm,将其绕它的一边所在的直线旋转一周,得到一个立体图形.
(1)得到的几何图形的名称为
圆柱 ,这个现象用数学知识解释为
面动成体 .
(2)求此几何体的表面积;(结果保留π)
(3)求此几何体的体积.(结果保留π)
【解析】解:(1)长方形绕一边旋转一周,得圆柱,
这个现象用数学知识解释为面动成体,
故答案为:圆柱,面动成体;
(2)①以长方形的长为轴旋转,则圆柱的底面半径r=4cm,
∴圆柱的表面积为:2πrl+2πr2=2π×4×5+2π×42=72π
(cm2);
②以长方形的宽为轴旋转,则圆柱的底面半径r=5cm,
∴圆柱的表面积为:2πrl+2πr2=2π×5×4+2π×52=90π
(cm2).
∴圆柱的表面积为72πcm2或90πcm2;
(3)分(2)中两种情况:
①圆柱的体积为V=πr2l=π×42×5=80π(
cm3);
②圆柱的体积为V=πr2l=π×52×4=100π
(cm3).
∴圆柱的体积为80πcm3或100πcm3.
21.(2020秋 铁岭月考)如图所示是长方体的表面展开图,折叠成一个长方体,那么:
(1)与N重合的点是哪几个?
(2)若AE=FH=14cm,FG=2cm,则该长方体的表面积和体积分别是多少?
【解析】(1)与N重合的点有点H和点J.
(2)有长方体展开图可知:FG=AB=CD=2cm,
∴AF=BC=DE=(14﹣2×2)÷2=5cm,
∴AH=FH﹣AF=14﹣5=9cm,
∴S=14×9+2×2×5=146cm2,
∴V=2×5×9=90cm3,
答:该长方体的表面积和体积分别为146cm2和90cm3.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
