北京101中学2022届高三上学期9月月考统练一数学试题(Word版,含答案)
文档属性
| 名称 | 北京101中学2022届高三上学期9月月考统练一数学试题(Word版,含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 670.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 00:00:00 | ||
图片预览



文档简介
2022届北京101中学高三(上)数学统练(一)
一、选择题共10小题.在每小题列出的四个选项中,选出符合题目要求的一项.
1.
设集合,,则(
)
A.
B.
C.
D.
2.
数列满足,,表示的前项和,且,则
A.
6
B.
7
C.
8
D.
9
3.
中,若,则的形状为
A.
直角三角形
B.
等腰三角形
C.
等边三角形
D.
锐角三角形
4.
若是上周期为5的奇函数,且满足,则.
A
6
B.
7
C.
8
D.
9
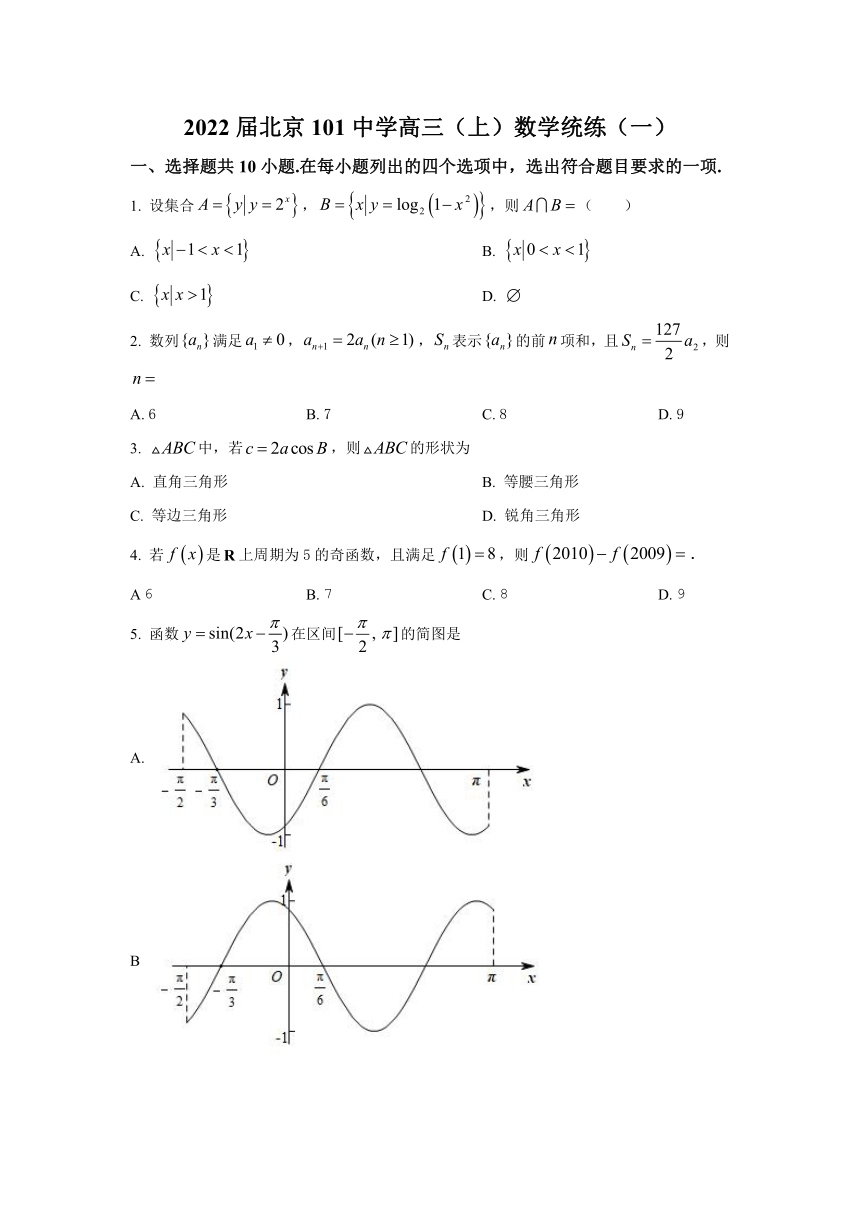
5.
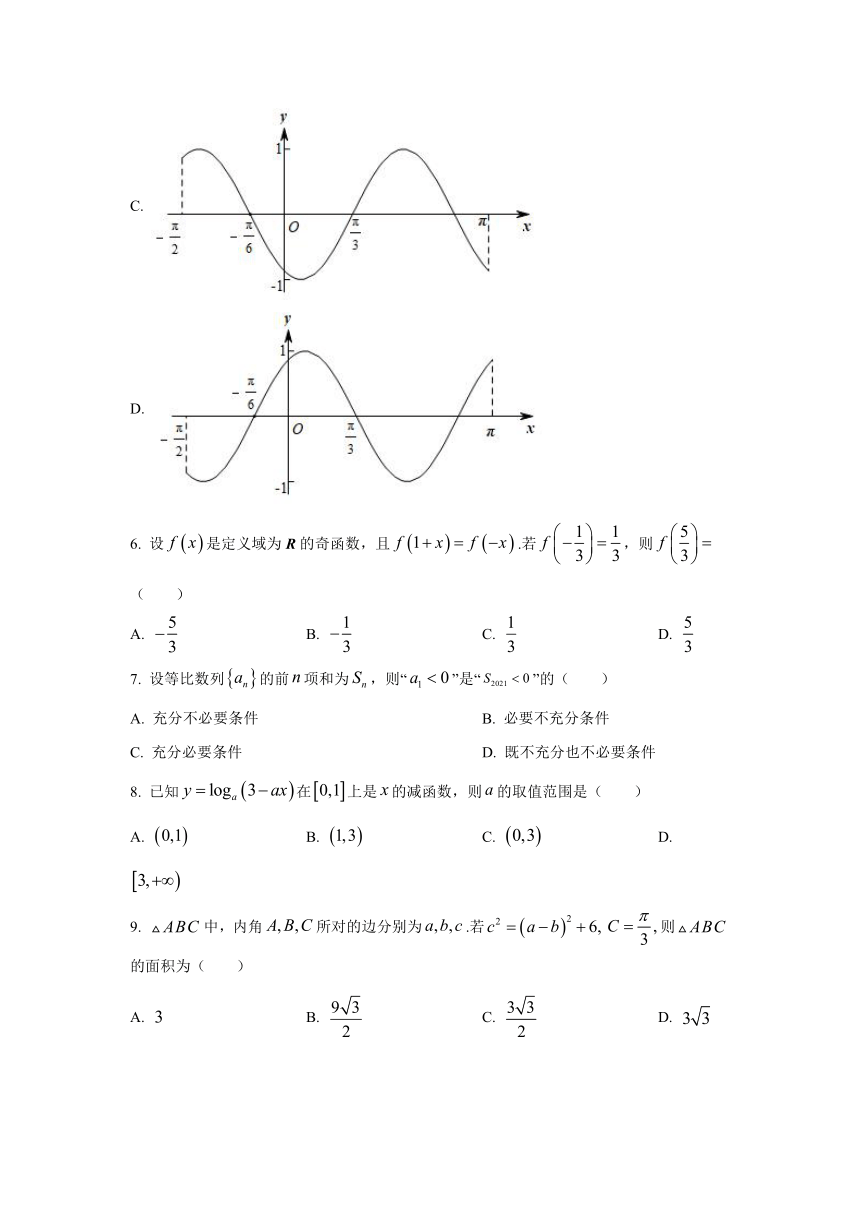
函数在区间的简图是
A.
B
C.
D.
6.
设是定义域为R的奇函数,且.若,则(
)
A.
B.
C.
D.
7.
设等比数列的前项和为,则“”是“”的(
)
A.
充分不必要条件
B.
必要不充分条件
C.
充分必要条件
D.
既不充分也不必要条件
8.
已知在上是的减函数,则的取值范围是(
)
A.
B.
C.
D.
9.
中,内角所对的边分别为.若则的面积为(
)
A.
B.
C.
D.
10.
已知函数,若对于任意正数,关于的方程都恰有两个不相等的实数根,则满足条件的实数的个数为(
)
A
B.
C.
D.
无数
二、填空题共5小题.
11.
已知为数列的前项和,若,则________.
12.
能够说明“若,,均为正数,则”是假命题的一组整数,,的值依次为__________.
13.
设函数,若对任意的实数x都成立,则的最小值为______.
14.
已知数列的通项公式,设其前项和为,则使成立的最小的自然为__________.
15.
一种药在病人血液中的量保持在以上时才有疗效,而低于时病人就有危险.现给某病人的静脉注射了这种药,如果药在血液中以每小时20%的比例衰减,设经过x小时后,药在病人血液中的量为.
(1)y关于x的函数解析式为______;
(2)要使病人没有危险,再次注射该药的时间不能超过______小时.(精确到0.1)(参考数据:,,,)
三、解答题共6小题.解答应写出文字说明、演算步骤或证明过程.
16.
已知函数.
(1)当时,求的值;
(2)当函数图象的两条相邻对称轴之间的距离是时,
.
从①②③中任选一个,补充到上面空格处并作答.①求在区间上的最小值;②求的单调递增区间;③若,求的取值范围.注:如果选择多个问题分别解答,按第一个解答计分.
17.
已知是各项均为正数的等比数列,,.
(Ⅰ)求的通项公式;
(Ⅱ)设,求数列的前项和,并求的最大值.
18.
在中,角的对边分别为,若.
(1)求角的大小;
(2)若,为外一点,,求四边形面积的最大值.
19.
已知函数.
(1)讨论的单调性;
(2)若有三个零点,求取值范围.
20.
已知函数.
(1)当时,求在处的切线方程;
(2)已知对任意恒成立,求的值.
21.
已知是无穷数列,,且对于中任意两项,在中都存在一项,使得.
(1)若,求;
(2)若,求证:数列中有无穷多项为;
(3)若,求数列的通项公式.
2022届北京101中学高三(上)数学统练(一)答案
一、选择题共10小题.在每小题列出的四个选项中,选出符合题目要求的一项.
1.
设集合,,则(
)
A.
B.
C.
D.
答案:B
2.
数列满足,,表示的前项和,且,则
A.
6
B.
7
C.
8
D.
9
答案:B
3.
中,若,则的形状为
A.
直角三角形
B.
等腰三角形
C.
等边三角形
D.
锐角三角形
答案:B
4.
若是上周期为5的奇函数,且满足,则.
A
6
B.
7
C.
8
D.
9
答案:C
5.
函数在区间的简图是
A.
B
C.
D.
答案:A
6.
设是定义域为R的奇函数,且.若,则(
)
A.
B.
C.
D.
答案:C
7.
设等比数列的前项和为,则“”是“”的(
)
A.
充分不必要条件
B.
必要不充分条件
C.
充分必要条件
D.
既不充分也不必要条件
答案:C
8.
已知在上是的减函数,则的取值范围是(
)
A.
B.
C.
D.
答案:B
9.
中,内角所对的边分别为.若则的面积为(
)
A.
B.
C.
D.
答案:C
10.
已知函数,若对于任意正数,关于的方程都恰有两个不相等的实数根,则满足条件的实数的个数为(
)
A
B.
C.
D.
无数
答案:B
二、填空题共5小题.
11.
已知为数列的前项和,若,则________.
答案:32
12.
能够说明“若,,均为正数,则”是假命题的一组整数,,的值依次为__________.
答案:1,2,3.(答案不唯一)
13.
设函数,若对任意的实数x都成立,则的最小值为______.
答案:2
14.
已知数列的通项公式,设其前项和为,则使成立的最小的自然为__________.
答案:14
15.
一种药在病人血液中的量保持在以上时才有疗效,而低于时病人就有危险.现给某病人的静脉注射了这种药,如果药在血液中以每小时20%的比例衰减,设经过x小时后,药在病人血液中的量为.
(1)y关于x的函数解析式为______;
(2)要使病人没有危险,再次注射该药的时间不能超过______小时.(精确到0.1)(参考数据:,,,)
答案:
①.
②.
7.2
三、解答题共6小题.解答应写出文字说明、演算步骤或证明过程.
16.
已知函数.
(1)当时,求的值;
(2)当函数图象的两条相邻对称轴之间的距离是时,
.
从①②③中任选一个,补充到上面空格处并作答.①求在区间上的最小值;②求的单调递增区间;③若,求的取值范围.注:如果选择多个问题分别解答,按第一个解答计分.
答案:(1)2;(2)答案见解析.
17.
已知是各项均为正数的等比数列,,.
(Ⅰ)求的通项公式;
(Ⅱ)设,求数列的前项和,并求的最大值.
答案:(Ⅰ);(Ⅱ),最大值为
18.
在中,角的对边分别为,若.
(1)求角的大小;
(2)若,为外一点,,求四边形面积的最大值.
答案:(1)(2)
19.
已知函数.
(1)讨论的单调性;
(2)若有三个零点,求取值范围.
答案:(1)详见解析;(2)
20.
已知函数.
(1)当时,求在处的切线方程;
(2)已知对任意恒成立,求的值.
答案:(1);(2)1.
21.
已知是无穷数列,,且对于中任意两项,在中都存在一项,使得.
(1)若,求;
(2)若,求证:数列中有无穷多项为;
(3)若,求数列的通项公式.
答案:(1)7;(2)证明见解析;(3),.
一、选择题共10小题.在每小题列出的四个选项中,选出符合题目要求的一项.
1.
设集合,,则(
)
A.
B.
C.
D.
2.
数列满足,,表示的前项和,且,则
A.
6
B.
7
C.
8
D.
9
3.
中,若,则的形状为
A.
直角三角形
B.
等腰三角形
C.
等边三角形
D.
锐角三角形
4.
若是上周期为5的奇函数,且满足,则.
A
6
B.
7
C.
8
D.
9
5.
函数在区间的简图是
A.
B
C.
D.
6.
设是定义域为R的奇函数,且.若,则(
)
A.
B.
C.
D.
7.
设等比数列的前项和为,则“”是“”的(
)
A.
充分不必要条件
B.
必要不充分条件
C.
充分必要条件
D.
既不充分也不必要条件
8.
已知在上是的减函数,则的取值范围是(
)
A.
B.
C.
D.
9.
中,内角所对的边分别为.若则的面积为(
)
A.
B.
C.
D.
10.
已知函数,若对于任意正数,关于的方程都恰有两个不相等的实数根,则满足条件的实数的个数为(
)
A
B.
C.
D.
无数
二、填空题共5小题.
11.
已知为数列的前项和,若,则________.
12.
能够说明“若,,均为正数,则”是假命题的一组整数,,的值依次为__________.
13.
设函数,若对任意的实数x都成立,则的最小值为______.
14.
已知数列的通项公式,设其前项和为,则使成立的最小的自然为__________.
15.
一种药在病人血液中的量保持在以上时才有疗效,而低于时病人就有危险.现给某病人的静脉注射了这种药,如果药在血液中以每小时20%的比例衰减,设经过x小时后,药在病人血液中的量为.
(1)y关于x的函数解析式为______;
(2)要使病人没有危险,再次注射该药的时间不能超过______小时.(精确到0.1)(参考数据:,,,)
三、解答题共6小题.解答应写出文字说明、演算步骤或证明过程.
16.
已知函数.
(1)当时,求的值;
(2)当函数图象的两条相邻对称轴之间的距离是时,
.
从①②③中任选一个,补充到上面空格处并作答.①求在区间上的最小值;②求的单调递增区间;③若,求的取值范围.注:如果选择多个问题分别解答,按第一个解答计分.
17.
已知是各项均为正数的等比数列,,.
(Ⅰ)求的通项公式;
(Ⅱ)设,求数列的前项和,并求的最大值.
18.
在中,角的对边分别为,若.
(1)求角的大小;
(2)若,为外一点,,求四边形面积的最大值.
19.
已知函数.
(1)讨论的单调性;
(2)若有三个零点,求取值范围.
20.
已知函数.
(1)当时,求在处的切线方程;
(2)已知对任意恒成立,求的值.
21.
已知是无穷数列,,且对于中任意两项,在中都存在一项,使得.
(1)若,求;
(2)若,求证:数列中有无穷多项为;
(3)若,求数列的通项公式.
2022届北京101中学高三(上)数学统练(一)答案
一、选择题共10小题.在每小题列出的四个选项中,选出符合题目要求的一项.
1.
设集合,,则(
)
A.
B.
C.
D.
答案:B
2.
数列满足,,表示的前项和,且,则
A.
6
B.
7
C.
8
D.
9
答案:B
3.
中,若,则的形状为
A.
直角三角形
B.
等腰三角形
C.
等边三角形
D.
锐角三角形
答案:B
4.
若是上周期为5的奇函数,且满足,则.
A
6
B.
7
C.
8
D.
9
答案:C
5.
函数在区间的简图是
A.
B
C.
D.
答案:A
6.
设是定义域为R的奇函数,且.若,则(
)
A.
B.
C.
D.
答案:C
7.
设等比数列的前项和为,则“”是“”的(
)
A.
充分不必要条件
B.
必要不充分条件
C.
充分必要条件
D.
既不充分也不必要条件
答案:C
8.
已知在上是的减函数,则的取值范围是(
)
A.
B.
C.
D.
答案:B
9.
中,内角所对的边分别为.若则的面积为(
)
A.
B.
C.
D.
答案:C
10.
已知函数,若对于任意正数,关于的方程都恰有两个不相等的实数根,则满足条件的实数的个数为(
)
A
B.
C.
D.
无数
答案:B
二、填空题共5小题.
11.
已知为数列的前项和,若,则________.
答案:32
12.
能够说明“若,,均为正数,则”是假命题的一组整数,,的值依次为__________.
答案:1,2,3.(答案不唯一)
13.
设函数,若对任意的实数x都成立,则的最小值为______.
答案:2
14.
已知数列的通项公式,设其前项和为,则使成立的最小的自然为__________.
答案:14
15.
一种药在病人血液中的量保持在以上时才有疗效,而低于时病人就有危险.现给某病人的静脉注射了这种药,如果药在血液中以每小时20%的比例衰减,设经过x小时后,药在病人血液中的量为.
(1)y关于x的函数解析式为______;
(2)要使病人没有危险,再次注射该药的时间不能超过______小时.(精确到0.1)(参考数据:,,,)
答案:
①.
②.
7.2
三、解答题共6小题.解答应写出文字说明、演算步骤或证明过程.
16.
已知函数.
(1)当时,求的值;
(2)当函数图象的两条相邻对称轴之间的距离是时,
.
从①②③中任选一个,补充到上面空格处并作答.①求在区间上的最小值;②求的单调递增区间;③若,求的取值范围.注:如果选择多个问题分别解答,按第一个解答计分.
答案:(1)2;(2)答案见解析.
17.
已知是各项均为正数的等比数列,,.
(Ⅰ)求的通项公式;
(Ⅱ)设,求数列的前项和,并求的最大值.
答案:(Ⅰ);(Ⅱ),最大值为
18.
在中,角的对边分别为,若.
(1)求角的大小;
(2)若,为外一点,,求四边形面积的最大值.
答案:(1)(2)
19.
已知函数.
(1)讨论的单调性;
(2)若有三个零点,求取值范围.
答案:(1)详见解析;(2)
20.
已知函数.
(1)当时,求在处的切线方程;
(2)已知对任意恒成立,求的值.
答案:(1);(2)1.
21.
已知是无穷数列,,且对于中任意两项,在中都存在一项,使得.
(1)若,求;
(2)若,求证:数列中有无穷多项为;
(3)若,求数列的通项公式.
答案:(1)7;(2)证明见解析;(3),.
同课章节目录
