3.2.3函数的奇偶性 课件(共25张PPT)
文档属性
| 名称 | 3.2.3函数的奇偶性 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 11:52:49 | ||
图片预览


文档简介
(共25张PPT)
3.2.2函数的奇偶性
人教A(2019)版
必修一
新知导入
日常生活中对称的美
从生活中这些图片中你感受到了什么?
新知讲解
一、函数奇偶性概念形成
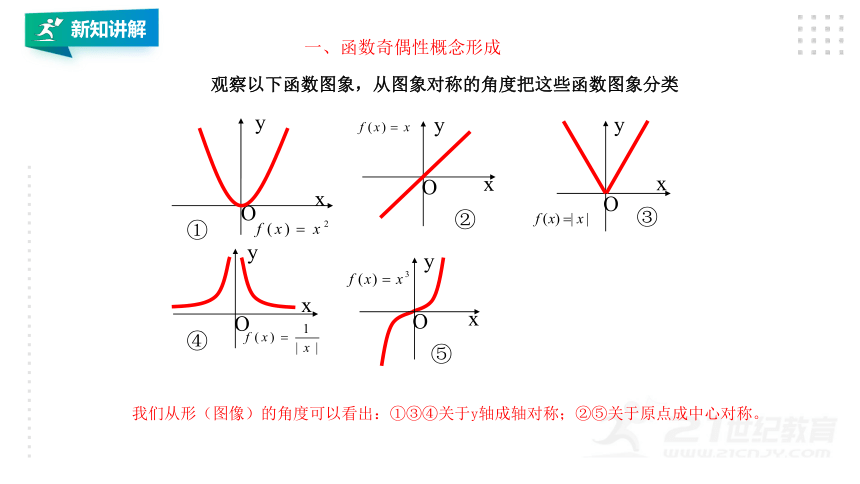
观察以下函数图象,从图象对称的角度把这些函数图象分类
O
x
y
①
②
O
x
y
③
O
x
y
④
O
x
y
O
x
y
⑤
我们从形(图像)的角度可以看出:①③④关于y轴成轴对称;②⑤关于原点成中心对称。
新知讲解
我们再从数的角度探讨它们的特征
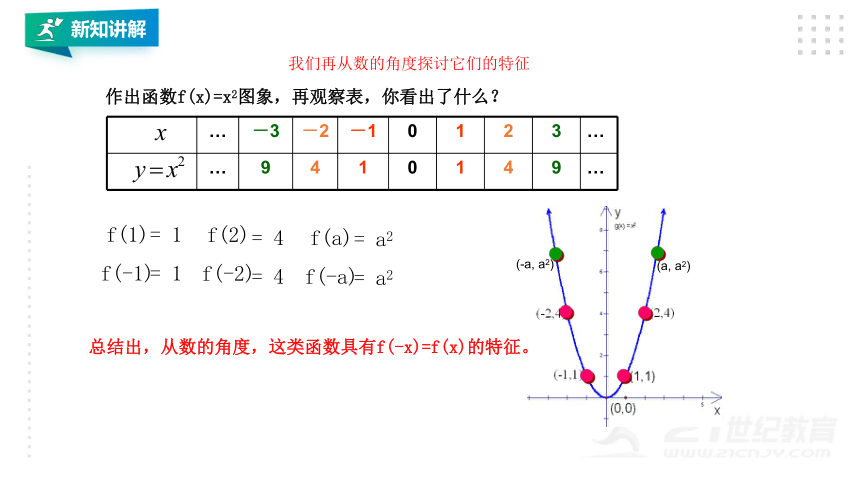
作出函数f(x)=x2图象,再观察表,你看出了什么?
…
-3
-2
-1
0
1
2
3
…
…
9
4
1
0
1
4
9
…
f(1)
f(-1)
=
1
=
1
f(a)
f(-a)
=
a2
=
a2
f(2)
f(-2)
=
4
=
4
(-a,
a2)
(a,
a2)
总结出,从数的角度,这类函数具有f(-x)=f(x)的特征。
新知讲解
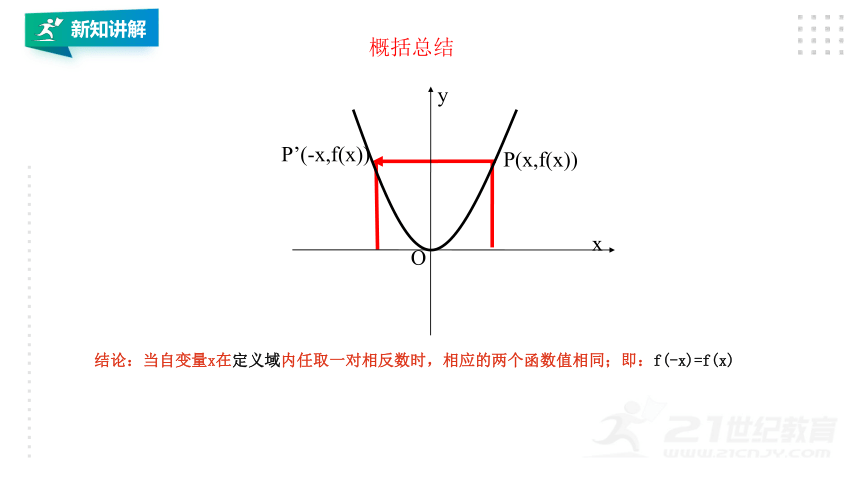
概括总结
P(x,f(x))
P’(-x,f(x))
O
x
y
结论:当自变量x在定义域内任取一对相反数时,相应的两个函数值相同;即:f(-x)=f(x)
新知讲解
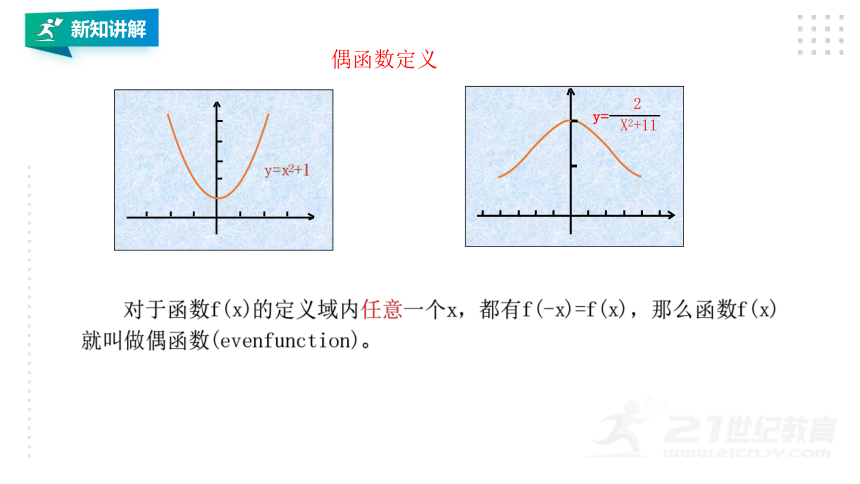
偶函数定义
-3
-2
-1
1
2
3
x
y
5
4
3
2
1
o
y=x2+1
y=x2+1
-5
-4-3-2-1
1
2
3
4
5
x
0.20
0.10
o
y=
2
X2+11
2
y=
对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)
就叫做偶函数(evenfunction)。
新知讲解
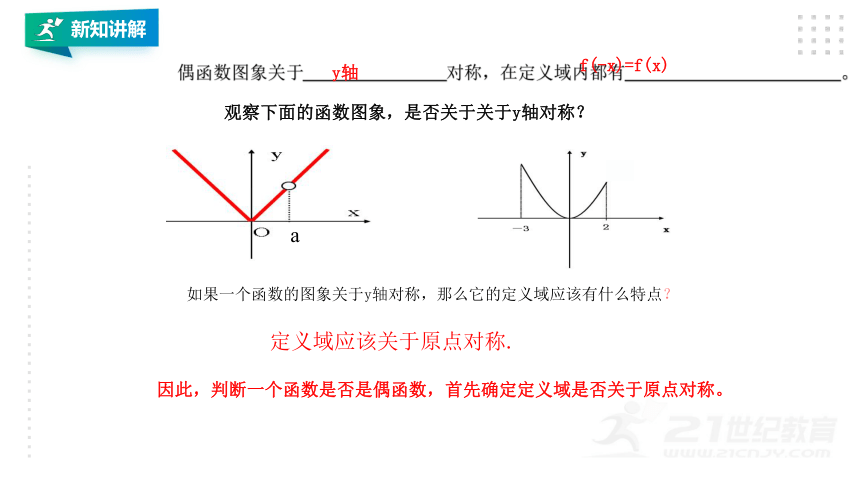
偶函数图象关于
对称,在定义域内都有
。
y轴
f(-x)=f(x)
观察下面的函数图象,是否关于关于y轴对称?
a
如果一个函数的图象关于y轴对称,那么它的定义域应该有什么特点?
定义域应该关于原点对称.
因此,判断一个函数是否是偶函数,首先确定定义域是否关于原点对称。
新知讲解
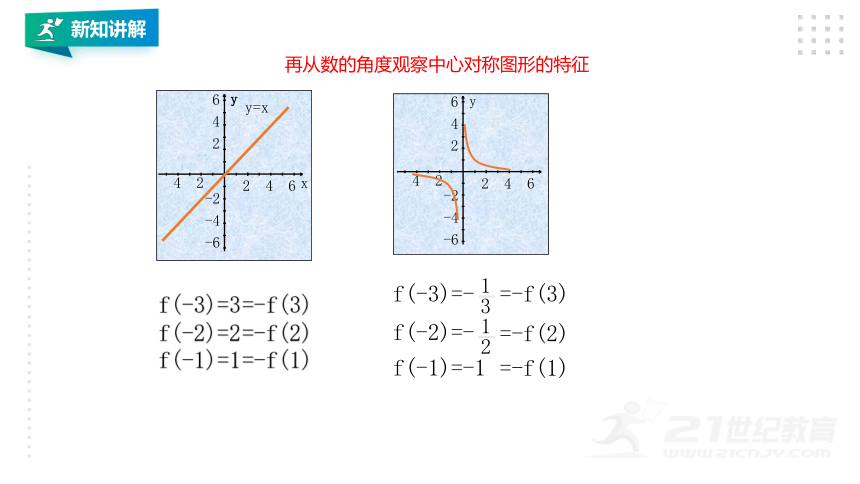
再从数的角度观察中心对称图形的特征
2
4
6
6
4
2
-2
-4
-6
4
2
x
y
y=x
f(-3)=3
=-f(3)
f(-2)=2
f(-1)=1
=-f(2)
=-f(1)
2
4
6
6
4
2
-2
-4
-6
4
2
x
y
y=
1
x
=-f(3)
f(-1)=-1
=-f(2)
=-f(1)
f(-3)=-
1
3
f(-2)=-
1
2
新知讲解
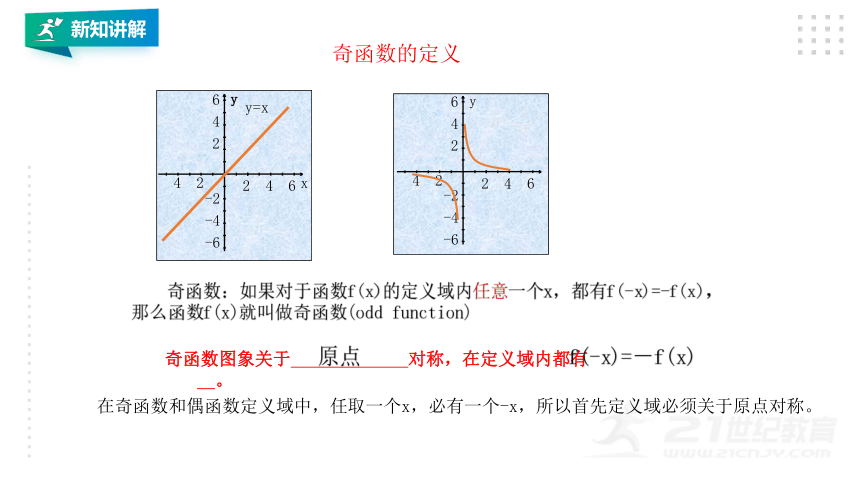
奇函数的定义
2
4
6
6
4
2
-2
-4
-6
4
2
x
y
y=x
2
4
6
6
4
2
-2
-4
-6
4
2
x
y
y=
1
x
奇函数:如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),
那么函数f(x)就叫做奇函数(odd
function)
奇函数图象关于
对称,在定义域内都有
。
原点
f(-x)=-f(x)
在奇函数和偶函数定义域中,任取一个x,必有一个-x,所以首先定义域必须关于原点对称。
新知讲解
(1)f(x)=x在区间[-1,3]上是奇函数吗?
(2)f(x)=x2在区间(-2,4)上是偶函数吗?
如果函数的定义域关于原点不对称,
那么它们在这个定义域内不具有奇偶性,
这个函数既不是奇函数也不是偶函数。
对于奇、偶函数定义的几点重要说明:
(1)
定义域关于原点对称是函数具有奇偶性的先决条件。
[a
,b]
[-b,-a]
x
o
(2)
如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇
偶性;否则不具备奇偶性。
(3)
函数的奇偶性是函数的整体性质.是对函数的整个定义域而言的.
1、判断下列函数的奇偶性:
(1)f(x)=x4
(2)f(x)=x+
(3)f(x)=
1
x2
1
x
(2)对于函数f(x)=x+
,其定义域为{x|x≠0}
1
x
解:(1)函数f(x)=x4,其定义域为(-∞,+∞)
因为定义域内的每一个x,都有:
f(-x)=
(-x)4=
x4=
f(x)
所以函数f(x)=x4是偶函数。
因为定义域内的每一个x,都有:
(-x)+
=
(-x)
1
f(-x)=
-f(x)
-(x+
)=
1
x
所以函数f(x)=x+
是奇函数。
1
x
(3)对于函数f(x)=
,其定义域为{x|x≠0}
1
x2
因为定义域内的每一个x,都有:
f(-x)=
f(x)
=
(-x)2
1
=
1
x2
所以函数f(x)=
是偶函数。
1
x2
合作探究
2、已知f(x),g(x)是定义域为R的函数,并且f(x)是偶函数,g(x)是奇函数,试将下图补充完整。
y
x
y
x
o
o
f(x)
g(x)
合作探究
合作探究
对于一些较复杂的函数,也可以用如下性质判断函数的奇偶性:
(1)偶函数的和、差、积、商(分母不为零)仍为偶函数;
(2)奇函数的和、差仍为奇函数;
(3)奇(偶)数个奇函数的积、商(分母不为零)为奇(偶)函数;
(4)一个奇函数与一个偶函数的积为奇函数.
试一试效果如何.判断下列函数的奇偶性
(1)
f(x)=x3-
2x;
(2)
f(x)=2x4+3x2
奇
偶
(3)
f(x)=-x|x|
(4)
f(x)=x2-2|x|+1
奇
偶
(5)
f(x)=x+x3+x5
奇
(6)
f(x)=x2
x∈[-
1
,
3]
非奇非偶
例、已知f(x)是奇函数,且当x>0时,f(x)=x|x-2|,求当x<0时,f(x)的表达式.
解:令x<0,则-x>0.
∴f(-x)=-x|-x-2|=-x|x+2|.
∵f(x)为奇函数,∴f(-x)=-f(x).
∴f(x)=x|x+2|.
故当x<0时,f(x)的表达式为f(x)=x|x+2|.
由函数奇偶性求函数解析式时
(1)若f(x)是奇函数,且已知x>0时的解析式,则x<0时的解析式只需将原函数
式y=f(x)中的x,y分别替换为-x,-y,然后解出y即可.
(2)若f(x)是偶函数,且已知x>0时的解析式,则x<0时的解析式只需将原函数
式y=f(x)中的x替换为-x,y不变,即得x<0时的解析式.
合作探究
新知讲解
二、偶函数的性质
1、偶函数关于y轴对称。
2、偶函数在关于原点的对称区间上单调性相反。
3、函数f(x)是偶函数,则f(-x)=f(x)=f(|x|)
例、若函数f(x)是定义在R上的偶函数,且在(-∞,0]上是增函数,若f(2)=0,则使f(x)<0的x的取值范围是( )
A.(-∞,2)
B.(-2,2)
C.(-∞,-2)∪(2,+∞)
D.(2,+∞)
解析:因为f(2)=0,所以f(x)<0即f(x)又由第二条性质,f(x)在[0,+∞]上是减函数,所以有|x|>2
故选C
新知讲解
三、奇函数的性质
1、奇函数图像关于原点成中心对称图形。
2、若0在定义域内,则必有f(0)=0
3、在关于原点的对称区间上单调性相同。特别地,如果f(x)在[0,a]上单调,则f(x)
在[-a,a]上有相同的单调性。
4、如果奇函数f(x)存在最大值则必存在最小值,且fmax(x)+fmin(x)=0
例、设定义在[-2,2]上的奇函数f(x)在区间[0,2]上是减函数,若f(1-m)解:因为f(x)是奇函数且f(x)在[0,2]上是减函数,所以f(x)在[-2,2]上是减函数.
注意:不能漏掉函数自身定义域对参数的影响.
合作探究
1、有下列说法:
①偶函数的图像一定与y轴相交;
②若y=f(x)是奇函数,则由f(-x)=-f(x)可知f(0)=0;
③既是奇函数也是偶函数的函数一定是f(x)=0,x∈R;
④若一个图形关于y轴成轴对称,则该图形一定是偶函数的图像.
其中不正确的是( )
A.①②
B.①④
C.①②④
D.①②③④
解析:①中可举反例f(x)=x2+2,x∈(-∞,-2)∪(2,+∞);②中f(x)在x=0处可能无定义;③中也可以
是f(x)=0,x∈A(A为关于原点对称的数集);④中该图形可能不是函数的图像.故①②③
④均错误.
答案:D
课堂练习
1.若f(x)=x5+5x3+bx-8,且f(-2)=10,求f(2)的值
解:令g(x)=x5+5x3+bx,则g(x)为奇函数。f(x)=g(x)-8,
f(-2)=g(-2)-8=10,即g(-2)=-g(2)=18,所以g(2)=-18
f(2)=g(2)-8=-18-8=-26
2.已知函数f(x)是定义在R上的偶函数,当x∈(-∞,0)时,f(x)=x-x4;当x∈(0,+∞)时,f(x)= .
解析:方法一:由于是填空题,故可采用直接代换法,将x用-x代替,
即答案为-x-x4.
-x-x4.
方法二:设x∈(0,+∞),则-x∈(-∞,0),
则f(-x)=-x-(-x)4=-x-x4.
又y=f(x)是偶函数,∴f(x)=f(-x).
∴f(x)在区间(0,+∞)上的函数表达式为f(x)=-x-x4.
3.函数f(x)(x∈R),若对任意实数a,b都有f(a+b)=f(a)+f(b),求证:f(x)为奇函数.
证明:令a=0,则f(b)=f(0)+f(b),∴f(0)=0.
又令a=-x,b=x,代入f(a+b)=f(a)+f(b),
得f(-x+x)=f(-x)+f(x).
即f(-x)+f(x)=0,∴f(-x)=-f(x).
∴f(x)为奇函数.
4.奇函数f(x)的定义域为[-5,5],它在y轴右侧的图像如图所示,则f(x)<0的x的
取值集合为
.
解析:奇函数f(x)在[-5,5]上的图像如图所示,由图像可知,x∈(2,5)时,f(x)<0;x∈(0,2)时,f(x)>0.
因为其图像关于原点对称,所以x∈(-5,-2)时,f(x)>0;x∈(-2,0)时,f(x)<0,所以使f(x)<0的x
的取值集合为{x|-2答案:{x|-2{x|-2课堂总结
奇偶性
奇函数
偶函数
定
义
设函数y=f(x)的定义域为D,
,都有
.
f(-x)=-f(x)
f(-x)=f(x)
图
像
性
质
关于原点对称
关于y轴对称
判断
步骤
定义域是否关于原点对称.
f(-x)=-f(x)
f(-x)=f(x)
x
o
y
(a,f(a))
(-a,f(-a))
-a
a
x
o
y
-a
a
(a,f(a))
(-a,f(-a))
课堂总结
奇函数性质
1、奇函数图像关于原点成中心对称图形。
2、若0在定义域内,则必有f(0)=0
3、在关于原点的对称区间上单调性相同。
特别地,如果f(x)在[0,a]上单调,则f(x)
在[-a,a]上有相同的单调性。
4、如果奇函数f(x)存在最大值则必存在最小
值,且fmax(x)+fmin(x)=0
偶函数的性质
1、偶函数关于y轴对称。
2、偶函数在关于原点的对称区
间上单调性相反。
3、函数f(x)是偶函数,则f(-x)=f(x)=f(|x|)
板书设计
函数的奇偶性
偶函数
奇函数
定义
判断方法及要领
性质
对于函数f(x)的定义域内任意一个x,都有
f(-x)=f(x),那么函数f(x)就叫做偶函数
如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数
一看定义域
二找f(-x)与f(x)关系
三判断
作业布置
1、设f(x)是定义在R上的奇函数,当x>0时,f(x)=2x+1,求x<0时,
f(x)的解析式.
2、设f(x)是定义在R上的奇函数,当x>0时,f(x)=2x+1,求f(x)
的解析式.
3、课本P865、11、12
https://www.21cnjy.com/help/help_extract.php
3.2.2函数的奇偶性
人教A(2019)版
必修一
新知导入
日常生活中对称的美
从生活中这些图片中你感受到了什么?
新知讲解
一、函数奇偶性概念形成
观察以下函数图象,从图象对称的角度把这些函数图象分类
O
x
y
①
②
O
x
y
③
O
x
y
④
O
x
y
O
x
y
⑤
我们从形(图像)的角度可以看出:①③④关于y轴成轴对称;②⑤关于原点成中心对称。
新知讲解
我们再从数的角度探讨它们的特征
作出函数f(x)=x2图象,再观察表,你看出了什么?
…
-3
-2
-1
0
1
2
3
…
…
9
4
1
0
1
4
9
…
f(1)
f(-1)
=
1
=
1
f(a)
f(-a)
=
a2
=
a2
f(2)
f(-2)
=
4
=
4
(-a,
a2)
(a,
a2)
总结出,从数的角度,这类函数具有f(-x)=f(x)的特征。
新知讲解
概括总结
P(x,f(x))
P’(-x,f(x))
O
x
y
结论:当自变量x在定义域内任取一对相反数时,相应的两个函数值相同;即:f(-x)=f(x)
新知讲解
偶函数定义
-3
-2
-1
1
2
3
x
y
5
4
3
2
1
o
y=x2+1
y=x2+1
-5
-4-3-2-1
1
2
3
4
5
x
0.20
0.10
o
y=
2
X2+11
2
y=
对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)
就叫做偶函数(evenfunction)。
新知讲解
偶函数图象关于
对称,在定义域内都有
。
y轴
f(-x)=f(x)
观察下面的函数图象,是否关于关于y轴对称?
a
如果一个函数的图象关于y轴对称,那么它的定义域应该有什么特点?
定义域应该关于原点对称.
因此,判断一个函数是否是偶函数,首先确定定义域是否关于原点对称。
新知讲解
再从数的角度观察中心对称图形的特征
2
4
6
6
4
2
-2
-4
-6
4
2
x
y
y=x
f(-3)=3
=-f(3)
f(-2)=2
f(-1)=1
=-f(2)
=-f(1)
2
4
6
6
4
2
-2
-4
-6
4
2
x
y
y=
1
x
=-f(3)
f(-1)=-1
=-f(2)
=-f(1)
f(-3)=-
1
3
f(-2)=-
1
2
新知讲解
奇函数的定义
2
4
6
6
4
2
-2
-4
-6
4
2
x
y
y=x
2
4
6
6
4
2
-2
-4
-6
4
2
x
y
y=
1
x
奇函数:如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),
那么函数f(x)就叫做奇函数(odd
function)
奇函数图象关于
对称,在定义域内都有
。
原点
f(-x)=-f(x)
在奇函数和偶函数定义域中,任取一个x,必有一个-x,所以首先定义域必须关于原点对称。
新知讲解
(1)f(x)=x在区间[-1,3]上是奇函数吗?
(2)f(x)=x2在区间(-2,4)上是偶函数吗?
如果函数的定义域关于原点不对称,
那么它们在这个定义域内不具有奇偶性,
这个函数既不是奇函数也不是偶函数。
对于奇、偶函数定义的几点重要说明:
(1)
定义域关于原点对称是函数具有奇偶性的先决条件。
[a
,b]
[-b,-a]
x
o
(2)
如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇
偶性;否则不具备奇偶性。
(3)
函数的奇偶性是函数的整体性质.是对函数的整个定义域而言的.
1、判断下列函数的奇偶性:
(1)f(x)=x4
(2)f(x)=x+
(3)f(x)=
1
x2
1
x
(2)对于函数f(x)=x+
,其定义域为{x|x≠0}
1
x
解:(1)函数f(x)=x4,其定义域为(-∞,+∞)
因为定义域内的每一个x,都有:
f(-x)=
(-x)4=
x4=
f(x)
所以函数f(x)=x4是偶函数。
因为定义域内的每一个x,都有:
(-x)+
=
(-x)
1
f(-x)=
-f(x)
-(x+
)=
1
x
所以函数f(x)=x+
是奇函数。
1
x
(3)对于函数f(x)=
,其定义域为{x|x≠0}
1
x2
因为定义域内的每一个x,都有:
f(-x)=
f(x)
=
(-x)2
1
=
1
x2
所以函数f(x)=
是偶函数。
1
x2
合作探究
2、已知f(x),g(x)是定义域为R的函数,并且f(x)是偶函数,g(x)是奇函数,试将下图补充完整。
y
x
y
x
o
o
f(x)
g(x)
合作探究
合作探究
对于一些较复杂的函数,也可以用如下性质判断函数的奇偶性:
(1)偶函数的和、差、积、商(分母不为零)仍为偶函数;
(2)奇函数的和、差仍为奇函数;
(3)奇(偶)数个奇函数的积、商(分母不为零)为奇(偶)函数;
(4)一个奇函数与一个偶函数的积为奇函数.
试一试效果如何.判断下列函数的奇偶性
(1)
f(x)=x3-
2x;
(2)
f(x)=2x4+3x2
奇
偶
(3)
f(x)=-x|x|
(4)
f(x)=x2-2|x|+1
奇
偶
(5)
f(x)=x+x3+x5
奇
(6)
f(x)=x2
x∈[-
1
,
3]
非奇非偶
例、已知f(x)是奇函数,且当x>0时,f(x)=x|x-2|,求当x<0时,f(x)的表达式.
解:令x<0,则-x>0.
∴f(-x)=-x|-x-2|=-x|x+2|.
∵f(x)为奇函数,∴f(-x)=-f(x).
∴f(x)=x|x+2|.
故当x<0时,f(x)的表达式为f(x)=x|x+2|.
由函数奇偶性求函数解析式时
(1)若f(x)是奇函数,且已知x>0时的解析式,则x<0时的解析式只需将原函数
式y=f(x)中的x,y分别替换为-x,-y,然后解出y即可.
(2)若f(x)是偶函数,且已知x>0时的解析式,则x<0时的解析式只需将原函数
式y=f(x)中的x替换为-x,y不变,即得x<0时的解析式.
合作探究
新知讲解
二、偶函数的性质
1、偶函数关于y轴对称。
2、偶函数在关于原点的对称区间上单调性相反。
3、函数f(x)是偶函数,则f(-x)=f(x)=f(|x|)
例、若函数f(x)是定义在R上的偶函数,且在(-∞,0]上是增函数,若f(2)=0,则使f(x)<0的x的取值范围是( )
A.(-∞,2)
B.(-2,2)
C.(-∞,-2)∪(2,+∞)
D.(2,+∞)
解析:因为f(2)=0,所以f(x)<0即f(x)
故选C
新知讲解
三、奇函数的性质
1、奇函数图像关于原点成中心对称图形。
2、若0在定义域内,则必有f(0)=0
3、在关于原点的对称区间上单调性相同。特别地,如果f(x)在[0,a]上单调,则f(x)
在[-a,a]上有相同的单调性。
4、如果奇函数f(x)存在最大值则必存在最小值,且fmax(x)+fmin(x)=0
例、设定义在[-2,2]上的奇函数f(x)在区间[0,2]上是减函数,若f(1-m)
注意:不能漏掉函数自身定义域对参数的影响.
合作探究
1、有下列说法:
①偶函数的图像一定与y轴相交;
②若y=f(x)是奇函数,则由f(-x)=-f(x)可知f(0)=0;
③既是奇函数也是偶函数的函数一定是f(x)=0,x∈R;
④若一个图形关于y轴成轴对称,则该图形一定是偶函数的图像.
其中不正确的是( )
A.①②
B.①④
C.①②④
D.①②③④
解析:①中可举反例f(x)=x2+2,x∈(-∞,-2)∪(2,+∞);②中f(x)在x=0处可能无定义;③中也可以
是f(x)=0,x∈A(A为关于原点对称的数集);④中该图形可能不是函数的图像.故①②③
④均错误.
答案:D
课堂练习
1.若f(x)=x5+5x3+bx-8,且f(-2)=10,求f(2)的值
解:令g(x)=x5+5x3+bx,则g(x)为奇函数。f(x)=g(x)-8,
f(-2)=g(-2)-8=10,即g(-2)=-g(2)=18,所以g(2)=-18
f(2)=g(2)-8=-18-8=-26
2.已知函数f(x)是定义在R上的偶函数,当x∈(-∞,0)时,f(x)=x-x4;当x∈(0,+∞)时,f(x)= .
解析:方法一:由于是填空题,故可采用直接代换法,将x用-x代替,
即答案为-x-x4.
-x-x4.
方法二:设x∈(0,+∞),则-x∈(-∞,0),
则f(-x)=-x-(-x)4=-x-x4.
又y=f(x)是偶函数,∴f(x)=f(-x).
∴f(x)在区间(0,+∞)上的函数表达式为f(x)=-x-x4.
3.函数f(x)(x∈R),若对任意实数a,b都有f(a+b)=f(a)+f(b),求证:f(x)为奇函数.
证明:令a=0,则f(b)=f(0)+f(b),∴f(0)=0.
又令a=-x,b=x,代入f(a+b)=f(a)+f(b),
得f(-x+x)=f(-x)+f(x).
即f(-x)+f(x)=0,∴f(-x)=-f(x).
∴f(x)为奇函数.
4.奇函数f(x)的定义域为[-5,5],它在y轴右侧的图像如图所示,则f(x)<0的x的
取值集合为
.
解析:奇函数f(x)在[-5,5]上的图像如图所示,由图像可知,x∈(2,5)时,f(x)<0;x∈(0,2)时,f(x)>0.
因为其图像关于原点对称,所以x∈(-5,-2)时,f(x)>0;x∈(-2,0)时,f(x)<0,所以使f(x)<0的x
的取值集合为{x|-2
奇偶性
奇函数
偶函数
定
义
设函数y=f(x)的定义域为D,
,都有
.
f(-x)=-f(x)
f(-x)=f(x)
图
像
性
质
关于原点对称
关于y轴对称
判断
步骤
定义域是否关于原点对称.
f(-x)=-f(x)
f(-x)=f(x)
x
o
y
(a,f(a))
(-a,f(-a))
-a
a
x
o
y
-a
a
(a,f(a))
(-a,f(-a))
课堂总结
奇函数性质
1、奇函数图像关于原点成中心对称图形。
2、若0在定义域内,则必有f(0)=0
3、在关于原点的对称区间上单调性相同。
特别地,如果f(x)在[0,a]上单调,则f(x)
在[-a,a]上有相同的单调性。
4、如果奇函数f(x)存在最大值则必存在最小
值,且fmax(x)+fmin(x)=0
偶函数的性质
1、偶函数关于y轴对称。
2、偶函数在关于原点的对称区
间上单调性相反。
3、函数f(x)是偶函数,则f(-x)=f(x)=f(|x|)
板书设计
函数的奇偶性
偶函数
奇函数
定义
判断方法及要领
性质
对于函数f(x)的定义域内任意一个x,都有
f(-x)=f(x),那么函数f(x)就叫做偶函数
如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数
一看定义域
二找f(-x)与f(x)关系
三判断
作业布置
1、设f(x)是定义在R上的奇函数,当x>0时,f(x)=2x+1,求x<0时,
f(x)的解析式.
2、设f(x)是定义在R上的奇函数,当x>0时,f(x)=2x+1,求f(x)
的解析式.
3、课本P865、11、12
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
