2021-2022学年苏科版九年级数学上册2.3确定圆的条件 同步达标测评(word解析版)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学上册2.3确定圆的条件 同步达标测评(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 265.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 21:47:29 | ||
图片预览


文档简介
2021-2022学年苏科版九年级数学上册《2.3确定圆的条件》同步达标测评(附答案)
一.选择题(共12小题,满分48分)
1.若⊙P的半径为13,圆心P的坐标为(5,12),则平面直角坐标系的原点O与⊙P的位置关系是( )
A.在⊙P内
B.在⊙P上
C.在⊙P外
D.无法确定
2.P为⊙O所在平面一点,若点P到⊙O的最短距离为3,最长距离为5,则⊙O的半径为( )A.2
B.4
C.1或4
D.2或8
3.⊙O的直径为15cm,O点与P点的距离为8cm,点P的位置( )
A.在⊙O外
B.在⊙O上
C.在⊙O内
D.不能确定
4.已知⊙P的半径为5,点P的坐标为(2,1),点Q的坐标为(0,6),则点Q与⊙P的位置关系是( )
A.点Q在⊙P外
B.点Q在⊙P上
C.点Q在⊙P内
D.不能确定
5.A、B、C为平面上的三点,AB=2,BC=3,AC=5,则( )
A.可以画一个圆,使A、B、C都在圆周上
B.可以画一个圆,使A、B在圆周上,C在圆内
C.可以画一个圆,使A、C在圆周上,B在圆外
D.可以画一个圆,使A、C在圆周上,B在圆内
6.已知⊙O为△ABC的外接圆,圆心O在AB上,∠BAC的平分线AD交⊙O于D,交BC于E,⊙O半径为5,AC=6,连接OD交BC于F.则EF的长是( )
A.2
B.4
C.1
D.3
7.如图,将△ABC放在每个小正方形边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面半径是( )
A.
B.
C.2
D.
8.如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=65°,则∠BAC=( )
A.15°
B.25°
C.35°
D.45°
9.如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,则O也是下列哪个三角形的外心( )
A.△AED的外心
B.△AEB的外心
C.△ACD的外心
D.△BCD的外心
10.如图,△ABC为⊙O的内接三角形,若∠ADC=115°,则∠AOC的度数是( )
A.115°
B.130°
C.150°
D.100°
11.下面说法正确的是( )
A.三点确定一个圆
B.外心在三角形的内部
C.平分弦的直径垂直于弦
D.等弧所对的圆周角相等
12.给出下列说法:
①经过三点一定可以作圆;
②任何一个三角形一定有一个外接圆,而且只有一个外接圆;
③任意一个圆一定有一个内接三角形,而且只有一个内接三角形;
④三角形的外心到三角形三个顶点的距离相等,其中正确的有( )
A.4个
B.3个
C.2个
D.1个
二.填空题(共4小题,满分20分)
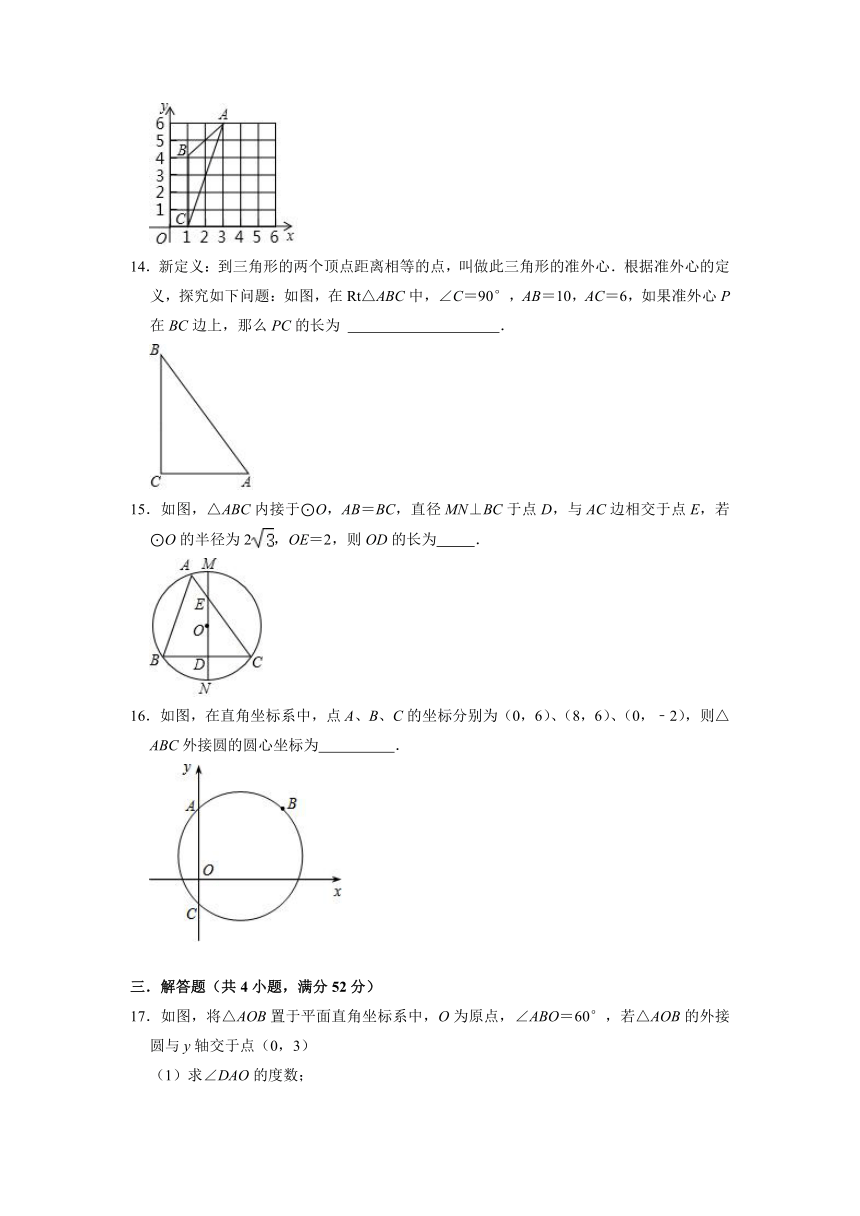
13.如图△ABC是坐标纸上的格点三角形,试写出△ABC外接圆的圆心坐标
.
14.新定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.根据准外心的定义,探究如下问题:如图,在Rt△ABC中,∠C=90°,AB=10,AC=6,如果准外心P在BC边上,那么PC的长为
.
15.如图,△ABC内接于⊙O,AB=BC,直径MN⊥BC于点D,与AC边相交于点E,若⊙O的半径为2,OE=2,则OD的长为
.
16.如图,在直角坐标系中,点A、B、C的坐标分别为(0,6)、(8,6)、(0,﹣2),则△ABC外接圆的圆心坐标为
.
三.解答题(共4小题,满分52分)
17.如图,将△AOB置于平面直角坐标系中,O为原点,∠ABO=60°,若△AOB的外接圆与y轴交于点(0,3)
(1)求∠DAO的度数;
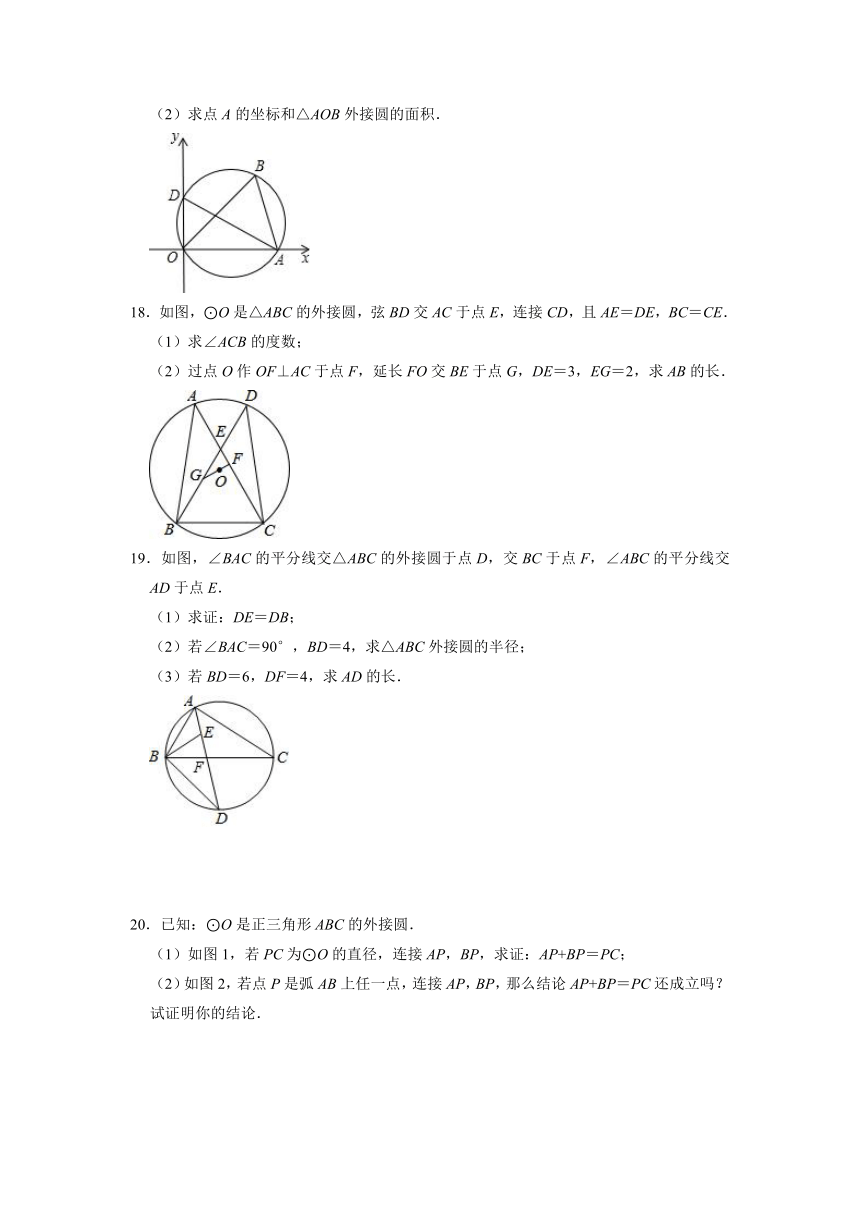
(2)求点A的坐标和△AOB外接圆的面积.
18.如图,⊙O是△ABC的外接圆,弦BD交AC于点E,连接CD,且AE=DE,BC=CE.
(1)求∠ACB的度数;
(2)过点O作OF⊥AC于点F,延长FO交BE于点G,DE=3,EG=2,求AB的长.
19.如图,∠BAC的平分线交△ABC的外接圆于点D,交BC于点F,∠ABC的平分线交AD于点E.
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径;
(3)若BD=6,DF=4,求AD的长.
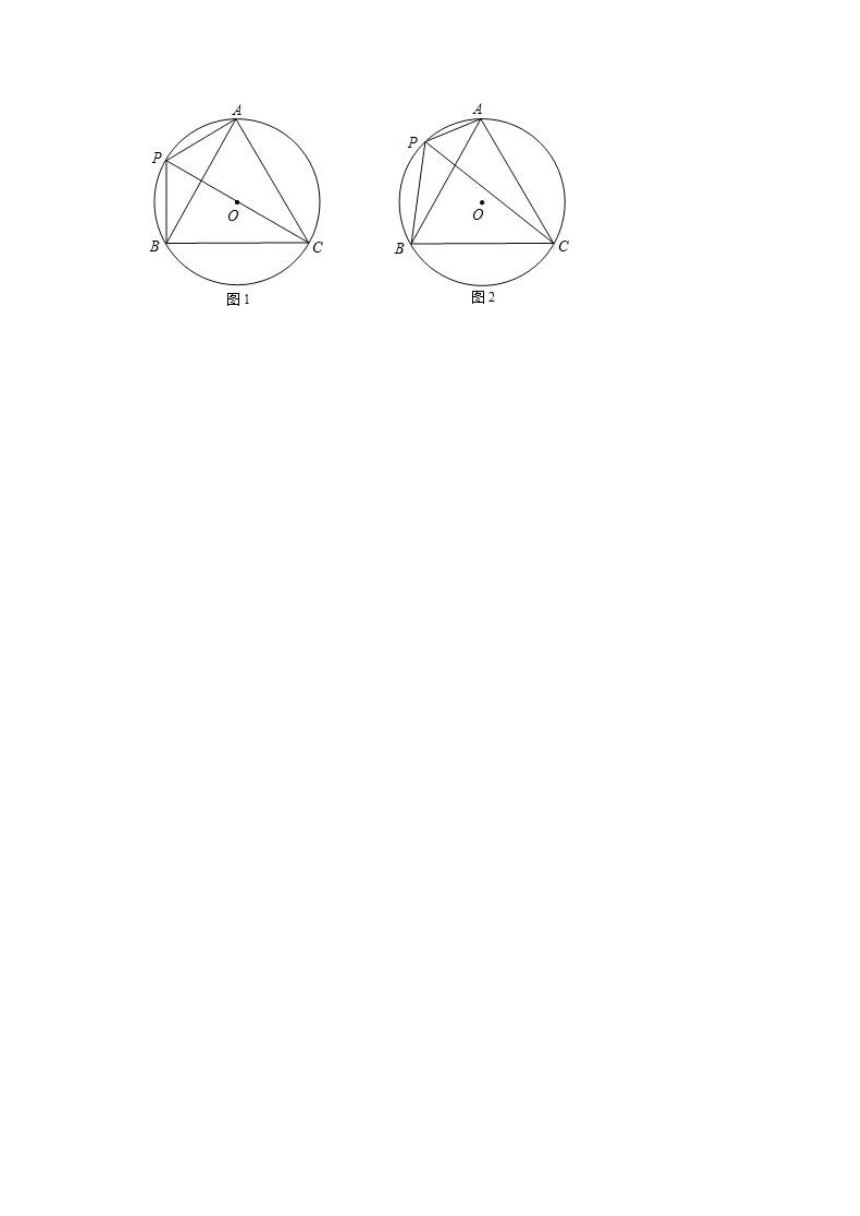
20.已知:⊙O是正三角形ABC的外接圆.
(1)如图1,若PC为⊙O的直径,连接AP,BP,求证:AP+BP=PC;
(2)如图2,若点P是弧AB上任一点,连接AP,BP,那么结论AP+BP=PC还成立吗?试证明你的结论.
参考答案
一.选择题(共12小题,满分48分)
1.解:∵圆心P的坐标为(5,12
),
∴OP==13,
∵⊙P的半径为13,
∴OP=r,
∴原点O在⊙P上.
故选:B.
2.解:当点P在圆内时,⊙O的直径长为3+5=8;
当点P在圆外时,⊙O的直径长为5﹣3=2;
即⊙O的半径长为4或1.
故选:C.
3.解:∵⊙O的直径为15cm,
∴⊙O的半径为7.5cm,
∵O点与P点的距离为8cm,
∴点P在⊙O外.
故选:A.
4.解:∵点P的坐标为(2,1),点Q的坐标为(0,6),
∴QP==>5,
∴点Q与⊙P的位置关系是:点Q在圆⊙P外.
故选:A.
5.解:∵A,B,C是平面内的三点,AB=2,BC=3,AC=5,
∴AB+BC=AC,
∴可以画一个圆,使A,C在圆上,B在圆内.
故选:D.
6.解:∵AD平分∠BAC,
∴∠DAC=∠BAD,
∵OA=OD,
∴∠OAD=∠D,
∴∠CAD=∠D,
∴AC∥OD,
∴OF=3,
∵FD=5﹣3=2,
在RT△OFB中,BF=,
∵OD⊥BC,
∴CF=BF=4,
∵AC∥OD,
∴,
∴EF=CF=×4=1.
故选:C.
7.解:如图所示:点O为△ABC外接圆圆心,则AO为外接圆半径,
故能够完全覆盖这个三角形的最小圆面的半径是:.
故选:A.
8.解:由圆周角定理得,∠ABC=∠ADC=65°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠BAC=90°﹣∠ABC=25°,
故选:B.
9.解:
连接OB、OD、OA,
∵O为锐角三角形ABC的外心,
∴OA=OC=OA,
∵四边形OCDE为正方形,
∴OA=OC<OD,
∴OA=OB=OC=OE≠OD,
A、OA=OE≠OD,即O不是△AED的外心,故本选项不符合题意;
B、OA=OE=OB,即O是△AEB的外心,故本选项符合题意;
C、OA=OC≠OD,即O不是△ACD的外心,故本选项不符合题意;
D、OB=OC≠OD,即O不是△BCD的外心,故本选项不符合题意;
故选:B.
10.解:∵四边形ABCD是⊙O的内接四边形,
∴∠B=180°﹣∠ADC=65°,
由圆周角定理得,∠AOC=2∠B=130°,
故选:B.
11.解:A、错误.理由是过不在同一直线上的三点确定一个圆.
B、错误.理由是钝角三角形的外心在三角形形外.
C、错误.平分弦(此弦非直径)的直径垂直于弦.
D、正确.等弧所对的圆周角相等.
12.解:①必须不在同一条直线上的三个点才能确定一个圆,故本选项错误;
②根据不在同一条直线上的三个点确定一个圆,故本选项正确;
③圆上有无数个点,任意连接3个点即是圆的一个内接三角形,故本选项错误;
④三角形的外心是三角形三条边垂直平分线的交点,所以到三角形三个顶点的距离相等,故本选项正确.
故选:C.
二.填空题(共4小题,满分20分)
13.解:由图象可知B(1,4),C(1,0),
根据△ABC的外接圆的定义,圆心的纵坐标是y=2,
设D(a,2),
根据勾股定理得:DA=DC
(1﹣a)2+22=42+(3﹣a)2
解得:a=5,
∴D(5,2).
故答案为:(5,2).
14.解:在Rt△ABC中,
∵C=90°,AB=10,AC=6,
∴BC===8,
若PB=PA,连接PA,
设PC=x,则PA=PB=8﹣x,
在Rt△PAC中,
∵PA2=CP2+AC2,
∴(8﹣x)2=x2+62,
∴x=,即PC=,
若PB=PC,则PC=4,
若PA=PC,由图知,在Rt△PAC中,不可能,
故PC的长为:4或.
故答案是:4或.
15.解:连接BO并延长交AC于F,如图,
∵BA=BC,
∴=,
∴BF⊥AC,
∵直径MN⊥BC,
∴BD=CD,
∵∠BOD=∠EOF,
设OF=x,则OD=x,
∵∠DBO=∠DEC,
BD=CD,
∴DB2=x(x+2)=3x2+2x,
在Rt△OBD中,3x2+2x+3x2=(2)2,解得x1=,x2=﹣(舍去),
∴OD=x=2.
故答案为2.
16.解:根据垂径定理的推论,则
作弦AB、AC的垂直平分线,交点O1即为圆心,
∵点A、B、C的坐标分别为(0,6)、(8,6)、(0,﹣2),
∴O1的坐标是(4,2).
故答案为:(4,2).
三.解答题(共4小题,满分52分)
17.解:(1)∵∠ADO=∠ABO=60°,∠AOD=90°,
∴∠DAO=30°.
(2)∵D的坐标是(0,3),则OD=3,
在直角△AOD中,OA=OD tan∠DAO=3,AD=2OD=6,
∴A的坐标是(3,0),△AOB外接圆的面积是9π.
18.(1)证明:在△AEB和△DEC中
,
∴△AEB≌△DEC(ASA),
∴EB=EC,
又∵BC=CE,
∴BE=CE=BC,
∴△EBC为等边三角形,
∴∠ACB=60°;
(2)解:作BM⊥AC于点M,
∵OF⊥AC,
∴AF=CF,
∵△EBC为等边三角形,
∴∠GEF=60°,
∴∠EGF=30°,
∵EG=2,
∴EF=1,
又∵AE=ED=3,
∴CF=AF=4,
∴AC=8,EC=5,
∴BC=5,
∵∠BCM=60°,
∴∠MBC=30°,
∴CM=,BM==,
∴AM=AC﹣CM=,
∴AB==7.
19.(1)证明:∵AD平分∠BAC,BE平分∠ABC,
∴∠1=∠2,∠3=∠4,
∴∠BED=∠1+∠3=∠2+∠4=∠5+∠4=∠DBE,
∴DB=DE;
(2)解:连接CD,如图,
∵∠BAC=90°,
∴BC为直径,
∴∠BDC=90°,
∵∠1=∠2,
∴DB=DC,
∴△DBC为等腰直角三角形,
∴BC=BD=4,
∴△ABC外接圆的半径为2;
(3)解:∵∠5=∠2=∠1,∠FDB=∠BDA,
∴AD=9.
20.证明:(1)∵△ABC为正三角形,
∴∠APC=∠BPC=60°,
∵PC为⊙O的直径,
∴∠PAC=∠PBC=90°,
∴AP=BP=PC,
∴AP+BP=PC;
(2)成立.
在PC上取一点D,使PD=PA,连接AD;
∵∠APD=60°,
∴△APD为等边三角形,
∴AD=PD;
∵∠PAD=∠BAC=60°,
∴∠PAB=∠DAC,
∵AP=AD,AB=AC,
∴△APB≌△ADC,
∴PB=DC,
∴PA+PB=PD+DC=PC.
一.选择题(共12小题,满分48分)
1.若⊙P的半径为13,圆心P的坐标为(5,12),则平面直角坐标系的原点O与⊙P的位置关系是( )
A.在⊙P内
B.在⊙P上
C.在⊙P外
D.无法确定
2.P为⊙O所在平面一点,若点P到⊙O的最短距离为3,最长距离为5,则⊙O的半径为( )A.2
B.4
C.1或4
D.2或8
3.⊙O的直径为15cm,O点与P点的距离为8cm,点P的位置( )
A.在⊙O外
B.在⊙O上
C.在⊙O内
D.不能确定
4.已知⊙P的半径为5,点P的坐标为(2,1),点Q的坐标为(0,6),则点Q与⊙P的位置关系是( )
A.点Q在⊙P外
B.点Q在⊙P上
C.点Q在⊙P内
D.不能确定
5.A、B、C为平面上的三点,AB=2,BC=3,AC=5,则( )
A.可以画一个圆,使A、B、C都在圆周上
B.可以画一个圆,使A、B在圆周上,C在圆内
C.可以画一个圆,使A、C在圆周上,B在圆外
D.可以画一个圆,使A、C在圆周上,B在圆内
6.已知⊙O为△ABC的外接圆,圆心O在AB上,∠BAC的平分线AD交⊙O于D,交BC于E,⊙O半径为5,AC=6,连接OD交BC于F.则EF的长是( )
A.2
B.4
C.1
D.3
7.如图,将△ABC放在每个小正方形边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面半径是( )
A.
B.
C.2
D.
8.如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=65°,则∠BAC=( )
A.15°
B.25°
C.35°
D.45°
9.如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,则O也是下列哪个三角形的外心( )
A.△AED的外心
B.△AEB的外心
C.△ACD的外心
D.△BCD的外心
10.如图,△ABC为⊙O的内接三角形,若∠ADC=115°,则∠AOC的度数是( )
A.115°
B.130°
C.150°
D.100°
11.下面说法正确的是( )
A.三点确定一个圆
B.外心在三角形的内部
C.平分弦的直径垂直于弦
D.等弧所对的圆周角相等
12.给出下列说法:
①经过三点一定可以作圆;
②任何一个三角形一定有一个外接圆,而且只有一个外接圆;
③任意一个圆一定有一个内接三角形,而且只有一个内接三角形;
④三角形的外心到三角形三个顶点的距离相等,其中正确的有( )
A.4个
B.3个
C.2个
D.1个
二.填空题(共4小题,满分20分)
13.如图△ABC是坐标纸上的格点三角形,试写出△ABC外接圆的圆心坐标
.
14.新定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.根据准外心的定义,探究如下问题:如图,在Rt△ABC中,∠C=90°,AB=10,AC=6,如果准外心P在BC边上,那么PC的长为
.
15.如图,△ABC内接于⊙O,AB=BC,直径MN⊥BC于点D,与AC边相交于点E,若⊙O的半径为2,OE=2,则OD的长为
.
16.如图,在直角坐标系中,点A、B、C的坐标分别为(0,6)、(8,6)、(0,﹣2),则△ABC外接圆的圆心坐标为
.
三.解答题(共4小题,满分52分)
17.如图,将△AOB置于平面直角坐标系中,O为原点,∠ABO=60°,若△AOB的外接圆与y轴交于点(0,3)
(1)求∠DAO的度数;
(2)求点A的坐标和△AOB外接圆的面积.
18.如图,⊙O是△ABC的外接圆,弦BD交AC于点E,连接CD,且AE=DE,BC=CE.
(1)求∠ACB的度数;
(2)过点O作OF⊥AC于点F,延长FO交BE于点G,DE=3,EG=2,求AB的长.
19.如图,∠BAC的平分线交△ABC的外接圆于点D,交BC于点F,∠ABC的平分线交AD于点E.
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径;
(3)若BD=6,DF=4,求AD的长.
20.已知:⊙O是正三角形ABC的外接圆.
(1)如图1,若PC为⊙O的直径,连接AP,BP,求证:AP+BP=PC;
(2)如图2,若点P是弧AB上任一点,连接AP,BP,那么结论AP+BP=PC还成立吗?试证明你的结论.
参考答案
一.选择题(共12小题,满分48分)
1.解:∵圆心P的坐标为(5,12
),
∴OP==13,
∵⊙P的半径为13,
∴OP=r,
∴原点O在⊙P上.
故选:B.
2.解:当点P在圆内时,⊙O的直径长为3+5=8;
当点P在圆外时,⊙O的直径长为5﹣3=2;
即⊙O的半径长为4或1.
故选:C.
3.解:∵⊙O的直径为15cm,
∴⊙O的半径为7.5cm,
∵O点与P点的距离为8cm,
∴点P在⊙O外.
故选:A.
4.解:∵点P的坐标为(2,1),点Q的坐标为(0,6),
∴QP==>5,
∴点Q与⊙P的位置关系是:点Q在圆⊙P外.
故选:A.
5.解:∵A,B,C是平面内的三点,AB=2,BC=3,AC=5,
∴AB+BC=AC,
∴可以画一个圆,使A,C在圆上,B在圆内.
故选:D.
6.解:∵AD平分∠BAC,
∴∠DAC=∠BAD,
∵OA=OD,
∴∠OAD=∠D,
∴∠CAD=∠D,
∴AC∥OD,
∴OF=3,
∵FD=5﹣3=2,
在RT△OFB中,BF=,
∵OD⊥BC,
∴CF=BF=4,
∵AC∥OD,
∴,
∴EF=CF=×4=1.
故选:C.
7.解:如图所示:点O为△ABC外接圆圆心,则AO为外接圆半径,
故能够完全覆盖这个三角形的最小圆面的半径是:.
故选:A.
8.解:由圆周角定理得,∠ABC=∠ADC=65°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠BAC=90°﹣∠ABC=25°,
故选:B.
9.解:
连接OB、OD、OA,
∵O为锐角三角形ABC的外心,
∴OA=OC=OA,
∵四边形OCDE为正方形,
∴OA=OC<OD,
∴OA=OB=OC=OE≠OD,
A、OA=OE≠OD,即O不是△AED的外心,故本选项不符合题意;
B、OA=OE=OB,即O是△AEB的外心,故本选项符合题意;
C、OA=OC≠OD,即O不是△ACD的外心,故本选项不符合题意;
D、OB=OC≠OD,即O不是△BCD的外心,故本选项不符合题意;
故选:B.
10.解:∵四边形ABCD是⊙O的内接四边形,
∴∠B=180°﹣∠ADC=65°,
由圆周角定理得,∠AOC=2∠B=130°,
故选:B.
11.解:A、错误.理由是过不在同一直线上的三点确定一个圆.
B、错误.理由是钝角三角形的外心在三角形形外.
C、错误.平分弦(此弦非直径)的直径垂直于弦.
D、正确.等弧所对的圆周角相等.
12.解:①必须不在同一条直线上的三个点才能确定一个圆,故本选项错误;
②根据不在同一条直线上的三个点确定一个圆,故本选项正确;
③圆上有无数个点,任意连接3个点即是圆的一个内接三角形,故本选项错误;
④三角形的外心是三角形三条边垂直平分线的交点,所以到三角形三个顶点的距离相等,故本选项正确.
故选:C.
二.填空题(共4小题,满分20分)
13.解:由图象可知B(1,4),C(1,0),
根据△ABC的外接圆的定义,圆心的纵坐标是y=2,
设D(a,2),
根据勾股定理得:DA=DC
(1﹣a)2+22=42+(3﹣a)2
解得:a=5,
∴D(5,2).
故答案为:(5,2).
14.解:在Rt△ABC中,
∵C=90°,AB=10,AC=6,
∴BC===8,
若PB=PA,连接PA,
设PC=x,则PA=PB=8﹣x,
在Rt△PAC中,
∵PA2=CP2+AC2,
∴(8﹣x)2=x2+62,
∴x=,即PC=,
若PB=PC,则PC=4,
若PA=PC,由图知,在Rt△PAC中,不可能,
故PC的长为:4或.
故答案是:4或.
15.解:连接BO并延长交AC于F,如图,
∵BA=BC,
∴=,
∴BF⊥AC,
∵直径MN⊥BC,
∴BD=CD,
∵∠BOD=∠EOF,
设OF=x,则OD=x,
∵∠DBO=∠DEC,
BD=CD,
∴DB2=x(x+2)=3x2+2x,
在Rt△OBD中,3x2+2x+3x2=(2)2,解得x1=,x2=﹣(舍去),
∴OD=x=2.
故答案为2.
16.解:根据垂径定理的推论,则
作弦AB、AC的垂直平分线,交点O1即为圆心,
∵点A、B、C的坐标分别为(0,6)、(8,6)、(0,﹣2),
∴O1的坐标是(4,2).
故答案为:(4,2).
三.解答题(共4小题,满分52分)
17.解:(1)∵∠ADO=∠ABO=60°,∠AOD=90°,
∴∠DAO=30°.
(2)∵D的坐标是(0,3),则OD=3,
在直角△AOD中,OA=OD tan∠DAO=3,AD=2OD=6,
∴A的坐标是(3,0),△AOB外接圆的面积是9π.
18.(1)证明:在△AEB和△DEC中
,
∴△AEB≌△DEC(ASA),
∴EB=EC,
又∵BC=CE,
∴BE=CE=BC,
∴△EBC为等边三角形,
∴∠ACB=60°;
(2)解:作BM⊥AC于点M,
∵OF⊥AC,
∴AF=CF,
∵△EBC为等边三角形,
∴∠GEF=60°,
∴∠EGF=30°,
∵EG=2,
∴EF=1,
又∵AE=ED=3,
∴CF=AF=4,
∴AC=8,EC=5,
∴BC=5,
∵∠BCM=60°,
∴∠MBC=30°,
∴CM=,BM==,
∴AM=AC﹣CM=,
∴AB==7.
19.(1)证明:∵AD平分∠BAC,BE平分∠ABC,
∴∠1=∠2,∠3=∠4,
∴∠BED=∠1+∠3=∠2+∠4=∠5+∠4=∠DBE,
∴DB=DE;
(2)解:连接CD,如图,
∵∠BAC=90°,
∴BC为直径,
∴∠BDC=90°,
∵∠1=∠2,
∴DB=DC,
∴△DBC为等腰直角三角形,
∴BC=BD=4,
∴△ABC外接圆的半径为2;
(3)解:∵∠5=∠2=∠1,∠FDB=∠BDA,
∴AD=9.
20.证明:(1)∵△ABC为正三角形,
∴∠APC=∠BPC=60°,
∵PC为⊙O的直径,
∴∠PAC=∠PBC=90°,
∴AP=BP=PC,
∴AP+BP=PC;
(2)成立.
在PC上取一点D,使PD=PA,连接AD;
∵∠APD=60°,
∴△APD为等边三角形,
∴AD=PD;
∵∠PAD=∠BAC=60°,
∴∠PAB=∠DAC,
∵AP=AD,AB=AC,
∴△APB≌△ADC,
∴PB=DC,
∴PA+PB=PD+DC=PC.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
