2021-2022学年苏科版九年级数学上册2.7弧长及扇形面积 知识点分类训练(Word版,含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学上册2.7弧长及扇形面积 知识点分类训练(Word版,含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 381.3KB | ||
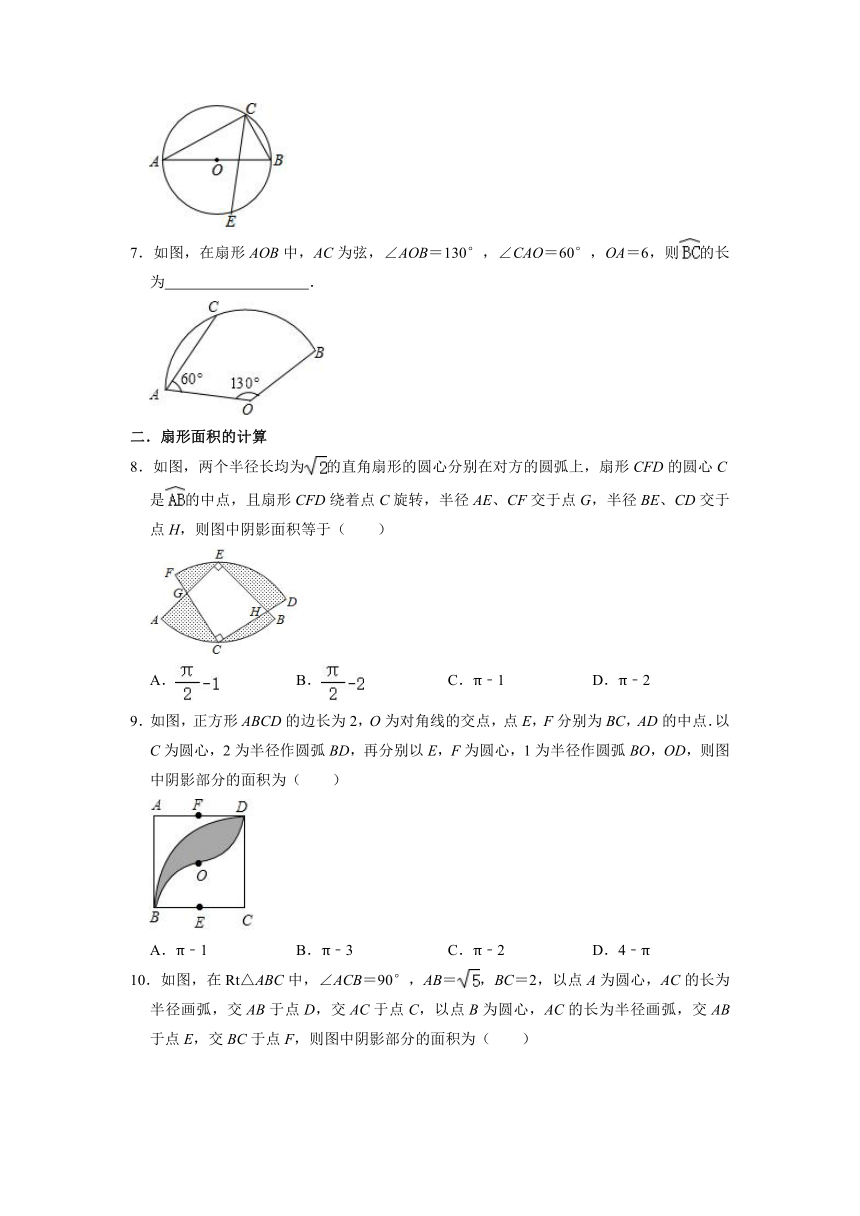
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 00:00:00 | ||
图片预览


文档简介
2021-2022学年苏科版九年级数学上册《2.7弧长及扇形面积》知识点分类训练(附答案)
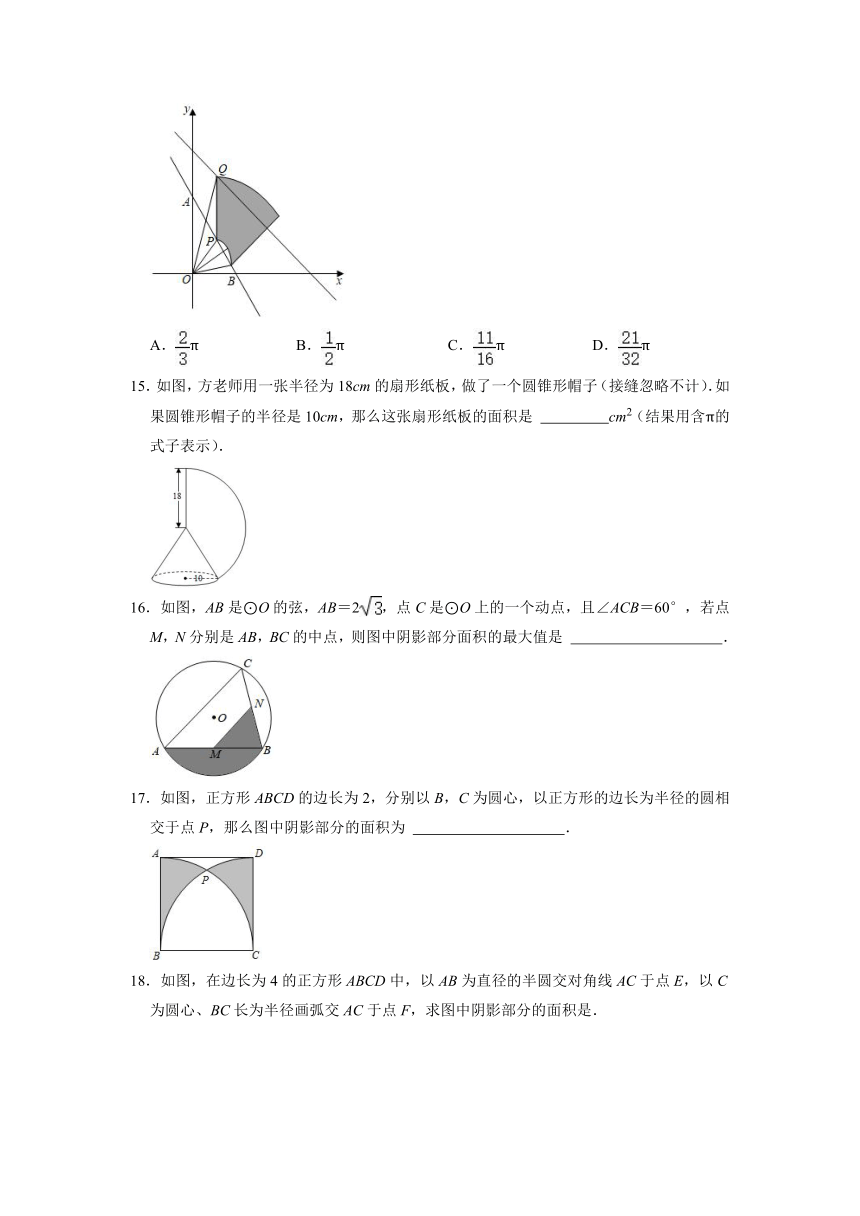
一.弧长的计算
1.一个扇形的弧长是8πcm,圆心角是144°,则此扇形的半径是
cm.
2.如图是圆弧形状的铁轨示意图,半径OA的长度为200米,圆心角∠AOB=90°,则这段铁轨的长度为
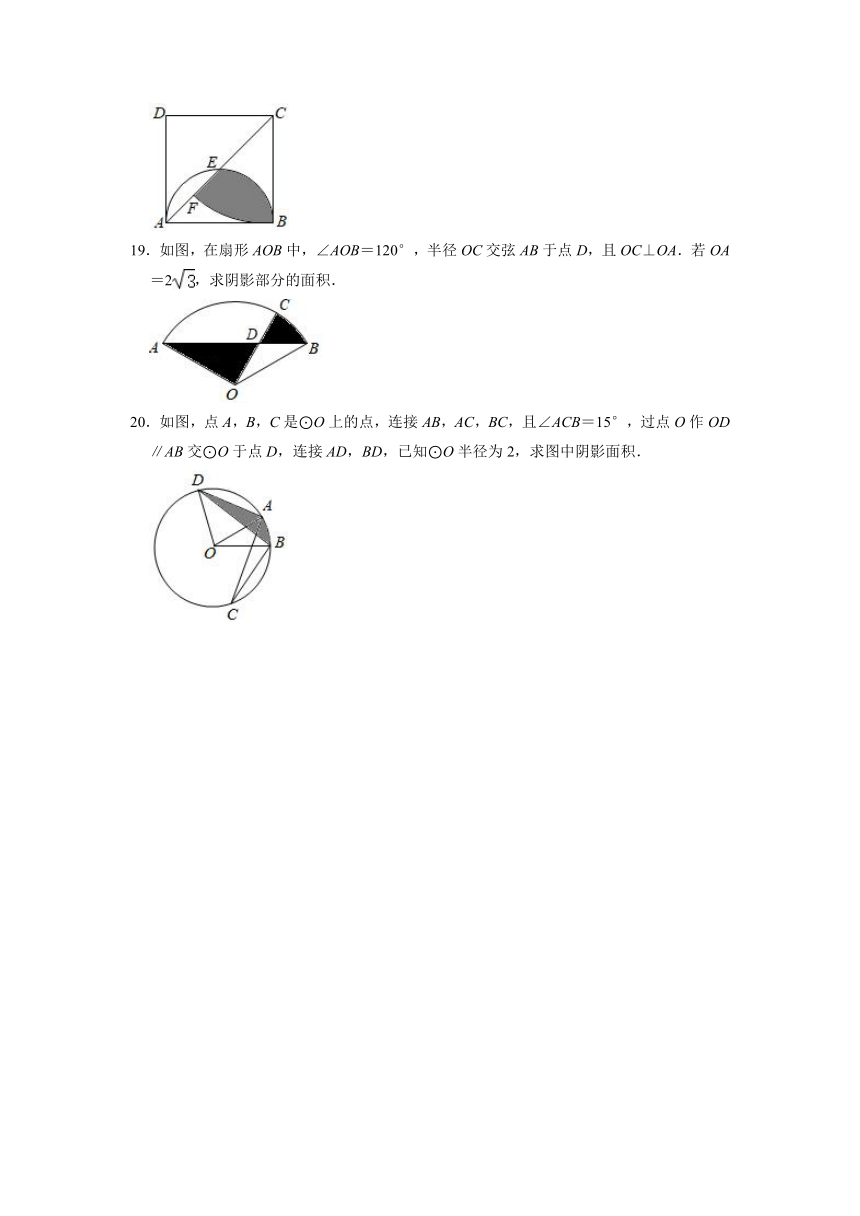
米.(铁轨的宽度忽略不计,结果保留π)
3.如图,在四边形ABCD中,AB=CB,AD=CD,我们把这种两组邻边分别相等的四边形叫做“筝形”.筝形ABCD的对角线AC,BD相交于点O.以点B为圆心,BO长为半径画弧,分别交AB,BC于点E,F.若∠ABD=∠ACD=30°,AD=1,则的长为
(结果保留π).
4.如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交于点D,点E为半径OB上一动点.若OB=2,则阴影部分周长的最小值为
.
5.如图,分别以正三角形的3个顶点为圆心,边长为半径画弧,三段弧围成的图形称为莱洛三角形.若正三角形边长为6cm,则该莱洛三角形的周长为
cm.
6.如图,已知AB为⊙O的直径,C为半圆上异于A、B的一个动点,∠ACB的平分线与⊙O交于点E,若圆的半径为2时,则的长度为
.
7.如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则的长为
.
二.扇形面积的计算
8.如图,两个半径长均为的直角扇形的圆心分别在对方的圆弧上,扇形CFD的圆心C是的中点,且扇形CFD绕着点C旋转,半径AE、CF交于点G,半径BE、CD交于点H,则图中阴影面积等于( )
A.
B.
C.π﹣1
D.π﹣2
9.如图,正方形ABCD的边长为2,O为对角线的交点,点E,F分别为BC,AD的中点.以C为圆心,2为半径作圆弧BD,再分别以E,F为圆心,1为半径作圆弧BO,OD,则图中阴影部分的面积为( )
A.π﹣1
B.π﹣3
C.π﹣2
D.4﹣π
10.如图,在Rt△ABC中,∠ACB=90°,AB=,BC=2,以点A为圆心,AC的长为半径画弧,交AB于点D,交AC于点C,以点B为圆心,AC的长为半径画弧,交AB于点E,交BC于点F,则图中阴影部分的面积为( )
A.8﹣π
B.4﹣π
C.2﹣
D.1﹣
11.如图所示,点A,B,C对应的刻度分别为1,3,5,将线段CA绕点C按顺时针方向旋转,当点A首次落在矩形BCDE的边BE上时,记为点A′,则此时线段CA扫过的图形的面积为( )
A.4
B.6
C.
D.
12.如图菱形ABCD中,∠D=60°,AB=2,以B为圆心、BC长为半径画,P为菱形内一点,连接PA,PB,PC.当△BPC为等腰直角三角形时,图中阴影部分面积为( )
A.
B.
C.2π
D.
13.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F,若⊙O的半径为4,∠CDF=15°,则阴影部分的面积为( )
A.16π﹣12
B.16π﹣24
C.20π﹣12
D.20π﹣24
14.如图,直线y=﹣2x+2与坐标轴交于A、B两点,点P是线段AB上的一个动点,过点P作y轴的平行线交直线y=﹣x+3于点Q,△OPQ绕点O顺时针旋转45°,边PQ扫过区域(阴影部分)面积的最大值是( )
A.π
B.π
C.π
D.π
15.如图,方老师用一张半径为18cm的扇形纸板,做了一个圆锥形帽子(接缝忽略不计).如果圆锥形帽子的半径是10cm,那么这张扇形纸板的面积是
cm2(结果用含π的式子表示).
16.如图,AB是⊙O的弦,AB=2,点C是⊙O上的一个动点,且∠ACB=60°,若点M,N分别是AB,BC的中点,则图中阴影部分面积的最大值是
.
17.如图,正方形ABCD的边长为2,分别以B,C为圆心,以正方形的边长为半径的圆相交于点P,那么图中阴影部分的面积为
.
18.如图,在边长为4的正方形ABCD中,以AB为直径的半圆交对角线AC于点E,以C为圆心、BC长为半径画弧交AC于点F,求图中阴影部分的面积是.
19.如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥OA.若OA=2,求阴影部分的面积.
20.如图,点A,B,C是⊙O上的点,连接AB,AC,BC,且∠ACB=15°,过点O作OD∥AB交⊙O于点D,连接AD,BD,已知⊙O半径为2,求图中阴影面积.
参考答案
一.弧长的计算
1.解:设扇形的半径为rcm,由题意得,
=8π,
解得r=10(cm),
故答案为:10.
2.解:圆弧长是:=100π(米).
故答案是:100π.
3.解:在△ABD与△CBD中,
,
∴△ABD≌△CBD(SSS),
∴∠ABD=∠CBD=30°,∠ADB=∠CDB,CD=AD=1,
∴∠ABC=60°,
∵AD=CD,∠ADB=∠CDB,
∴BD⊥AC,且AO=CO,
∴∠ACB=90°﹣30°=60°,
∴∠BCD=∠ACB+∠ACD=90°,
在Rt△BCD中,∵∠CBD=30°,
∴BD=2CD=2,
在Rt△COD中,∵∠ACD=30°,
∴OD=CD=,
∴OB=BD﹣OD=2﹣=,
∴的长为:=,
故答案为.
4.解:如图,作点D关于OB的对称点D′,连接D′C交OB于点E′,连接E′D、OD′,
此时E′C+E′D最小,即:E′C+E′D=CD′,
由题意得,∠COD=∠DOB=∠BOD′=30°,
∴∠COD′=90°,
∴CD′===2,
的长l==,
∴阴影部分周长的最小值为2+=.
故答案为:.
5.解:该莱洛三角形的周长=3×=6π(cm).
故答案为6π.
6.解:连接OE,如图所示:
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠ACB的平分线与⊙O交于点E,
∴∠ACE=∠ACB=45°,
∴∠AOE=2∠ACE=90°,
∴的长度为=π;
故答案为:π.
7.解:连接OC,如图,
∵OA=OC,
∴∠OCA=∠CAO=60°,
∴∠AOC=60°,
∴∠BOC=130°﹣60°=70°,
∴的长==π.
故答案为π.
二.扇形面积的计算
8.解:两扇形的面积和为:=π,
过点C作CM⊥AE,作CN⊥BE,垂足分别为M、N,
则四边形EMCN是矩形,
∵点C是的中点,
∴EC平分∠AEB,
∴CM=CN,
∴矩形EMCN是正方形,
∵∠MCG+∠FCN=90°,∠NCH+∠FCN=90°,
∴∠MCG=∠NCH,
在△CMG与△CNH中,
,
∴△CMG≌△CNH(ASA),
∴中间空白区域面积相当于对角线是的正方形面积,
∴空白区域的面积为:××=1,
∴图中阴影部分的面积=两个扇形面积和﹣2个空白区域面积的和=π﹣2.
故选:D.
9.解:连接BD,EF,如图,
∵正方形ABCD的边长为2,O为对角线的交点,
由题意可得:EF,BD经过点O,且EF⊥AD,EF⊥CB.
∵点E,F分别为BC,AD的中点,
∴FD=FO=EO=EB=1,
∴,OB=OD.
∴弓形OB=弓形OD.
∴阴影部分的面积等于弓形BD的面积.
∴S阴影=S扇形CBD﹣S△CBD==π﹣2.
故选:C.
10.解:根据题意可知AC===1,则BE=BF=AD=AC=1,
设∠B=n°,∠A=m°,
∵∠ACB=90°,
∴∠B+∠A=90°,即n+m=90,
∴S阴影部分=S△ABC﹣(S扇形EBF+S扇形DAC)=﹣()=1﹣=1﹣,
故选:D.
11.解:由题意,知AC=4,BC=4﹣2=2,∠A′BC=90°.
由旋转的性质,得A′C=AC=4.
在Rt△A1BC中,cos∠ACA′==.
∴∠ACA′=60°.
∴扇形ACA′的面积为=π.
即线段CA扫过的图形的面积为π.
故选:D.
12.解:连接AC,延长AP,交BC于E,
在菱形ABCD中,∠D=60°,AB=2,
∴∠ABC=∠D=60°,AB=BC=2,
∴△ABC是等边三角形,
∴AB=AC,
在△APB和△APC中,
,
∴△APB≌△APC(SSS),
∴∠PAB=∠PAC,
∴AE⊥BC,BE=CE=1,
∵△BPC为等腰直角三角形,
∴PE=BC=1,
在Rt△ABE中,AE=AB=,
∴AP=﹣1,
∴S阴影=S扇形ABC﹣S△PAB﹣S△PBC=﹣(﹣1)×1﹣=π﹣,
故选:A.
13.解:连接AD,OE
∵AB为直径,
∴∠ADB=∠ADC=90°,
∴∠ADF+∠CDF=90°,
∵DF⊥AC,
∴∠AFD=90°,
∴∠ADF+∠DAF=90°,
∴∠CDF=∠DAC,
∵∠CDF=15°,
∴∠DAC=15°,
∵AB=AC,AD⊥BC,
∴∠BAC=2∠DAC=30°,
∵OA=OE,
∴∠OAE=∠OEA=30°,
∴∠AOE=120°,
作OH⊥AE于H,
在Rt△AOH中,OA=4,
∴OH=2,
AH=6,
∴AE=2AH=12,
∴S阴影=S扇形OAE﹣S△AOE==16.
故选:A.
14.解:设P(m,﹣2m+2),则Q(m,﹣m+3).
∴OP2=m2+(﹣2m+2)2=5m2﹣8m+4,OQ2=m2+(﹣m+3)2=2m2﹣6m+9.
∵△OPQ绕点O顺时针旋转45°.
∴△OPQ≌△ODC,∠QOC=∠POD=45°.
∴PQ扫过区域(阴影部分)面积S=S扇OQC﹣S扇OPD===.
当m=时,S的最大值为:.
故选:A.
15.解:这张扇形纸板的面积=×2π×10×18=180π(cm2).
故答案为180π.
16.解:连接OA、OB、OM,如图,
∵∠ACB=60°,
∴∠AOB=120°,
∵OA=OB,
∴∠OAB=∠OBA=30°,
∵AM=BM=AB=,
∴OM⊥AB,
∴OM=×=1,
∴OA=2OM=2,
∵点M、N分别是AB、BC的中点,
∴MN∥AC,MN=AC,
∴当△ABC的面积最大时,△MBN的面积最大,
∵C、O、M在一条直线时,△ABC的面积最大,
∴△ABC的面积最大值为:××(2+1)=3,
∴△MBN的面积最大值为:,
∵S弓形=S扇形OAB﹣S△AOB=﹣=﹣,
∴此时,S阴影=﹣+=﹣,
故答案为:﹣.
17.解:连接PB、PC,作PF⊥BC于F,
∵PB=PC=BC,
∴△PBC为等边三角形,
∴∠PBC=60°,∠PBA=30°,
∴BF=PB=1,PF=,
则图中阴影部分的面积=[扇形ABP的面积﹣(扇形BPC的面积﹣△BPC的面积)]×2
=[﹣(﹣×2×)]×2=2﹣,
故答案为:2﹣.
18.解:连接BE,
∵AB为直径,
∴BE⊥AC,
∵AB=BC=4,∠ABC=90°,
∴BE=AE=CE,
∴S弓形AE=S弓形BE,
∴图中阴影部分的面积=S半圆﹣(S半圆﹣S△ABE)﹣(S△ABC﹣S扇形CBF)
=π×22﹣(﹣)﹣(﹣)
=3π﹣6,
故答案为3π﹣6.
19.解:作OE⊥AB于点F,
∵在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥OA.OA=2,
∴∠AOD=90°,∠BOC=30°,OA=OB,
∴∠OAB=∠OBA=30°,
∴OD=×=2,AD=4,AB=2AF=2×2×=6,OF=,
∴BD=2,
∴阴影部分的面积是:S△AOD+S扇形OBC﹣S△BDO==+π,
故答案为:+π.
20.解:∵∠ACB=15°,
∴∠AOB=30°,
∵OD∥AB,
∴S△ABD=S△ABO,
∴S阴影=S扇形AOB=.
故答案为:.
一.弧长的计算
1.一个扇形的弧长是8πcm,圆心角是144°,则此扇形的半径是
cm.
2.如图是圆弧形状的铁轨示意图,半径OA的长度为200米,圆心角∠AOB=90°,则这段铁轨的长度为
米.(铁轨的宽度忽略不计,结果保留π)
3.如图,在四边形ABCD中,AB=CB,AD=CD,我们把这种两组邻边分别相等的四边形叫做“筝形”.筝形ABCD的对角线AC,BD相交于点O.以点B为圆心,BO长为半径画弧,分别交AB,BC于点E,F.若∠ABD=∠ACD=30°,AD=1,则的长为
(结果保留π).
4.如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交于点D,点E为半径OB上一动点.若OB=2,则阴影部分周长的最小值为
.
5.如图,分别以正三角形的3个顶点为圆心,边长为半径画弧,三段弧围成的图形称为莱洛三角形.若正三角形边长为6cm,则该莱洛三角形的周长为
cm.
6.如图,已知AB为⊙O的直径,C为半圆上异于A、B的一个动点,∠ACB的平分线与⊙O交于点E,若圆的半径为2时,则的长度为
.
7.如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则的长为
.
二.扇形面积的计算
8.如图,两个半径长均为的直角扇形的圆心分别在对方的圆弧上,扇形CFD的圆心C是的中点,且扇形CFD绕着点C旋转,半径AE、CF交于点G,半径BE、CD交于点H,则图中阴影面积等于( )
A.
B.
C.π﹣1
D.π﹣2
9.如图,正方形ABCD的边长为2,O为对角线的交点,点E,F分别为BC,AD的中点.以C为圆心,2为半径作圆弧BD,再分别以E,F为圆心,1为半径作圆弧BO,OD,则图中阴影部分的面积为( )
A.π﹣1
B.π﹣3
C.π﹣2
D.4﹣π
10.如图,在Rt△ABC中,∠ACB=90°,AB=,BC=2,以点A为圆心,AC的长为半径画弧,交AB于点D,交AC于点C,以点B为圆心,AC的长为半径画弧,交AB于点E,交BC于点F,则图中阴影部分的面积为( )
A.8﹣π
B.4﹣π
C.2﹣
D.1﹣
11.如图所示,点A,B,C对应的刻度分别为1,3,5,将线段CA绕点C按顺时针方向旋转,当点A首次落在矩形BCDE的边BE上时,记为点A′,则此时线段CA扫过的图形的面积为( )
A.4
B.6
C.
D.
12.如图菱形ABCD中,∠D=60°,AB=2,以B为圆心、BC长为半径画,P为菱形内一点,连接PA,PB,PC.当△BPC为等腰直角三角形时,图中阴影部分面积为( )
A.
B.
C.2π
D.
13.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F,若⊙O的半径为4,∠CDF=15°,则阴影部分的面积为( )
A.16π﹣12
B.16π﹣24
C.20π﹣12
D.20π﹣24
14.如图,直线y=﹣2x+2与坐标轴交于A、B两点,点P是线段AB上的一个动点,过点P作y轴的平行线交直线y=﹣x+3于点Q,△OPQ绕点O顺时针旋转45°,边PQ扫过区域(阴影部分)面积的最大值是( )
A.π
B.π
C.π
D.π
15.如图,方老师用一张半径为18cm的扇形纸板,做了一个圆锥形帽子(接缝忽略不计).如果圆锥形帽子的半径是10cm,那么这张扇形纸板的面积是
cm2(结果用含π的式子表示).
16.如图,AB是⊙O的弦,AB=2,点C是⊙O上的一个动点,且∠ACB=60°,若点M,N分别是AB,BC的中点,则图中阴影部分面积的最大值是
.
17.如图,正方形ABCD的边长为2,分别以B,C为圆心,以正方形的边长为半径的圆相交于点P,那么图中阴影部分的面积为
.
18.如图,在边长为4的正方形ABCD中,以AB为直径的半圆交对角线AC于点E,以C为圆心、BC长为半径画弧交AC于点F,求图中阴影部分的面积是.
19.如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥OA.若OA=2,求阴影部分的面积.
20.如图,点A,B,C是⊙O上的点,连接AB,AC,BC,且∠ACB=15°,过点O作OD∥AB交⊙O于点D,连接AD,BD,已知⊙O半径为2,求图中阴影面积.
参考答案
一.弧长的计算
1.解:设扇形的半径为rcm,由题意得,
=8π,
解得r=10(cm),
故答案为:10.
2.解:圆弧长是:=100π(米).
故答案是:100π.
3.解:在△ABD与△CBD中,
,
∴△ABD≌△CBD(SSS),
∴∠ABD=∠CBD=30°,∠ADB=∠CDB,CD=AD=1,
∴∠ABC=60°,
∵AD=CD,∠ADB=∠CDB,
∴BD⊥AC,且AO=CO,
∴∠ACB=90°﹣30°=60°,
∴∠BCD=∠ACB+∠ACD=90°,
在Rt△BCD中,∵∠CBD=30°,
∴BD=2CD=2,
在Rt△COD中,∵∠ACD=30°,
∴OD=CD=,
∴OB=BD﹣OD=2﹣=,
∴的长为:=,
故答案为.
4.解:如图,作点D关于OB的对称点D′,连接D′C交OB于点E′,连接E′D、OD′,
此时E′C+E′D最小,即:E′C+E′D=CD′,
由题意得,∠COD=∠DOB=∠BOD′=30°,
∴∠COD′=90°,
∴CD′===2,
的长l==,
∴阴影部分周长的最小值为2+=.
故答案为:.
5.解:该莱洛三角形的周长=3×=6π(cm).
故答案为6π.
6.解:连接OE,如图所示:
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠ACB的平分线与⊙O交于点E,
∴∠ACE=∠ACB=45°,
∴∠AOE=2∠ACE=90°,
∴的长度为=π;
故答案为:π.
7.解:连接OC,如图,
∵OA=OC,
∴∠OCA=∠CAO=60°,
∴∠AOC=60°,
∴∠BOC=130°﹣60°=70°,
∴的长==π.
故答案为π.
二.扇形面积的计算
8.解:两扇形的面积和为:=π,
过点C作CM⊥AE,作CN⊥BE,垂足分别为M、N,
则四边形EMCN是矩形,
∵点C是的中点,
∴EC平分∠AEB,
∴CM=CN,
∴矩形EMCN是正方形,
∵∠MCG+∠FCN=90°,∠NCH+∠FCN=90°,
∴∠MCG=∠NCH,
在△CMG与△CNH中,
,
∴△CMG≌△CNH(ASA),
∴中间空白区域面积相当于对角线是的正方形面积,
∴空白区域的面积为:××=1,
∴图中阴影部分的面积=两个扇形面积和﹣2个空白区域面积的和=π﹣2.
故选:D.
9.解:连接BD,EF,如图,
∵正方形ABCD的边长为2,O为对角线的交点,
由题意可得:EF,BD经过点O,且EF⊥AD,EF⊥CB.
∵点E,F分别为BC,AD的中点,
∴FD=FO=EO=EB=1,
∴,OB=OD.
∴弓形OB=弓形OD.
∴阴影部分的面积等于弓形BD的面积.
∴S阴影=S扇形CBD﹣S△CBD==π﹣2.
故选:C.
10.解:根据题意可知AC===1,则BE=BF=AD=AC=1,
设∠B=n°,∠A=m°,
∵∠ACB=90°,
∴∠B+∠A=90°,即n+m=90,
∴S阴影部分=S△ABC﹣(S扇形EBF+S扇形DAC)=﹣()=1﹣=1﹣,
故选:D.
11.解:由题意,知AC=4,BC=4﹣2=2,∠A′BC=90°.
由旋转的性质,得A′C=AC=4.
在Rt△A1BC中,cos∠ACA′==.
∴∠ACA′=60°.
∴扇形ACA′的面积为=π.
即线段CA扫过的图形的面积为π.
故选:D.
12.解:连接AC,延长AP,交BC于E,
在菱形ABCD中,∠D=60°,AB=2,
∴∠ABC=∠D=60°,AB=BC=2,
∴△ABC是等边三角形,
∴AB=AC,
在△APB和△APC中,
,
∴△APB≌△APC(SSS),
∴∠PAB=∠PAC,
∴AE⊥BC,BE=CE=1,
∵△BPC为等腰直角三角形,
∴PE=BC=1,
在Rt△ABE中,AE=AB=,
∴AP=﹣1,
∴S阴影=S扇形ABC﹣S△PAB﹣S△PBC=﹣(﹣1)×1﹣=π﹣,
故选:A.
13.解:连接AD,OE
∵AB为直径,
∴∠ADB=∠ADC=90°,
∴∠ADF+∠CDF=90°,
∵DF⊥AC,
∴∠AFD=90°,
∴∠ADF+∠DAF=90°,
∴∠CDF=∠DAC,
∵∠CDF=15°,
∴∠DAC=15°,
∵AB=AC,AD⊥BC,
∴∠BAC=2∠DAC=30°,
∵OA=OE,
∴∠OAE=∠OEA=30°,
∴∠AOE=120°,
作OH⊥AE于H,
在Rt△AOH中,OA=4,
∴OH=2,
AH=6,
∴AE=2AH=12,
∴S阴影=S扇形OAE﹣S△AOE==16.
故选:A.
14.解:设P(m,﹣2m+2),则Q(m,﹣m+3).
∴OP2=m2+(﹣2m+2)2=5m2﹣8m+4,OQ2=m2+(﹣m+3)2=2m2﹣6m+9.
∵△OPQ绕点O顺时针旋转45°.
∴△OPQ≌△ODC,∠QOC=∠POD=45°.
∴PQ扫过区域(阴影部分)面积S=S扇OQC﹣S扇OPD===.
当m=时,S的最大值为:.
故选:A.
15.解:这张扇形纸板的面积=×2π×10×18=180π(cm2).
故答案为180π.
16.解:连接OA、OB、OM,如图,
∵∠ACB=60°,
∴∠AOB=120°,
∵OA=OB,
∴∠OAB=∠OBA=30°,
∵AM=BM=AB=,
∴OM⊥AB,
∴OM=×=1,
∴OA=2OM=2,
∵点M、N分别是AB、BC的中点,
∴MN∥AC,MN=AC,
∴当△ABC的面积最大时,△MBN的面积最大,
∵C、O、M在一条直线时,△ABC的面积最大,
∴△ABC的面积最大值为:××(2+1)=3,
∴△MBN的面积最大值为:,
∵S弓形=S扇形OAB﹣S△AOB=﹣=﹣,
∴此时,S阴影=﹣+=﹣,
故答案为:﹣.
17.解:连接PB、PC,作PF⊥BC于F,
∵PB=PC=BC,
∴△PBC为等边三角形,
∴∠PBC=60°,∠PBA=30°,
∴BF=PB=1,PF=,
则图中阴影部分的面积=[扇形ABP的面积﹣(扇形BPC的面积﹣△BPC的面积)]×2
=[﹣(﹣×2×)]×2=2﹣,
故答案为:2﹣.
18.解:连接BE,
∵AB为直径,
∴BE⊥AC,
∵AB=BC=4,∠ABC=90°,
∴BE=AE=CE,
∴S弓形AE=S弓形BE,
∴图中阴影部分的面积=S半圆﹣(S半圆﹣S△ABE)﹣(S△ABC﹣S扇形CBF)
=π×22﹣(﹣)﹣(﹣)
=3π﹣6,
故答案为3π﹣6.
19.解:作OE⊥AB于点F,
∵在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥OA.OA=2,
∴∠AOD=90°,∠BOC=30°,OA=OB,
∴∠OAB=∠OBA=30°,
∴OD=×=2,AD=4,AB=2AF=2×2×=6,OF=,
∴BD=2,
∴阴影部分的面积是:S△AOD+S扇形OBC﹣S△BDO==+π,
故答案为:+π.
20.解:∵∠ACB=15°,
∴∠AOB=30°,
∵OD∥AB,
∴S△ABD=S△ABO,
∴S阴影=S扇形AOB=.
故答案为:.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
