2021-2022学年数学人教B版(2019)选择性必修第一册第一章 空间向量与立体几何测试题(Word含答案)
文档属性
| 名称 | 2021-2022学年数学人教B版(2019)选择性必修第一册第一章 空间向量与立体几何测试题(Word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 514.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 19:20:23 | ||
图片预览


文档简介
单元测试题系列(十七)
第一章:空间向量与立体几何测试题
考试时间:80分钟,总分:100分
一、单项选择题:(每小题4分,共28分)
1.
长方体ABCD-A1B1C1D1中,化简(
)
。
A.
B.
C.
D.
2.已知=,=,若∥,则与的值分别
为(
)。
A、,
B、5,2
C、,
D、-5,-2
3.
已知正方体的棱长为1,且,,
,则
(
)
。B
A.1
B.2
C.-1
D.3
4、若平面的法向量为,直线的方向向量为,直线与平面的夹角为,则下列关系式中成立的是(
)。
A、
B、
C、
D、
5、若平面、的法向量分别为=(1,2,-2),=(-3,-6,6),则(
)。
A、∥
B、⊥
C、、相交但不垂直
D、都不正确
6、在正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么
直线AM和CN所成角的余弦值是(
)。
A、
B、
C、
D、
7、若直线的方向向量与平面的法向量的夹角等于120o,则直线与平面
所成的角等于(
)。
A、120o
B、60o
C、30o
D、以上均不正确
二、多项选择题:(每小题4分,共12分)
8.以下结论正确的有(
)。
A.对于任意向量,有=
B.已知两个非零向量,,在空间任取一点O,作=
,
=,则称作向量与向量的夹角
C.对于任意向量,总有||成立。
D.对于任意向量,总有⊥成立。
9、以下结论正确的有(
)。
A.如果∥,则存在唯一个实数,使
B.如果存在实数对,使成立,则向量一定共面
C.设{a,b,c}是空间向量的一个基底,若向量,同时,
则。
D.设{a,b,c}是空间向量的一个基底,如果a,b,c的模都为1,且两两互相垂直,则该基底叫单位正交基底。
10、若n1,n2分别是平面的法向量,且,,,则可以取的值为(
)。
A、1
B、-1
C、2
D、-2
注意:请将选择题答案填入下表:
题号
一、单项选择题
二、多项选择题
1
2
3
4
5
6
7
8
9
10
答案
三、填空题:(每小题4分,共20分)
11.已知正方体的棱长为1,且,,,则
。
12、已知四面体ABCD中,且,,,D为线段OA中点,E为线段BC的中点,则在基底{,,c}下的分解式为
。
13、已知a=(2
,4
,x),b=(2
,y
,2),若|a|=6且a⊥b,则x+y等于
。
14、直线的一个方向向量为,平面内两个不共线向量为。已知直线不在平面内,且,则直线与平面的关系为
。
15、已知平面内的一条直线与平面的一条斜线的夹角为,这条直线与斜线在平面内的射影的夹角为,则斜线与平面所成角的大小为
。
四、解答题:(每小题10分,共40分)
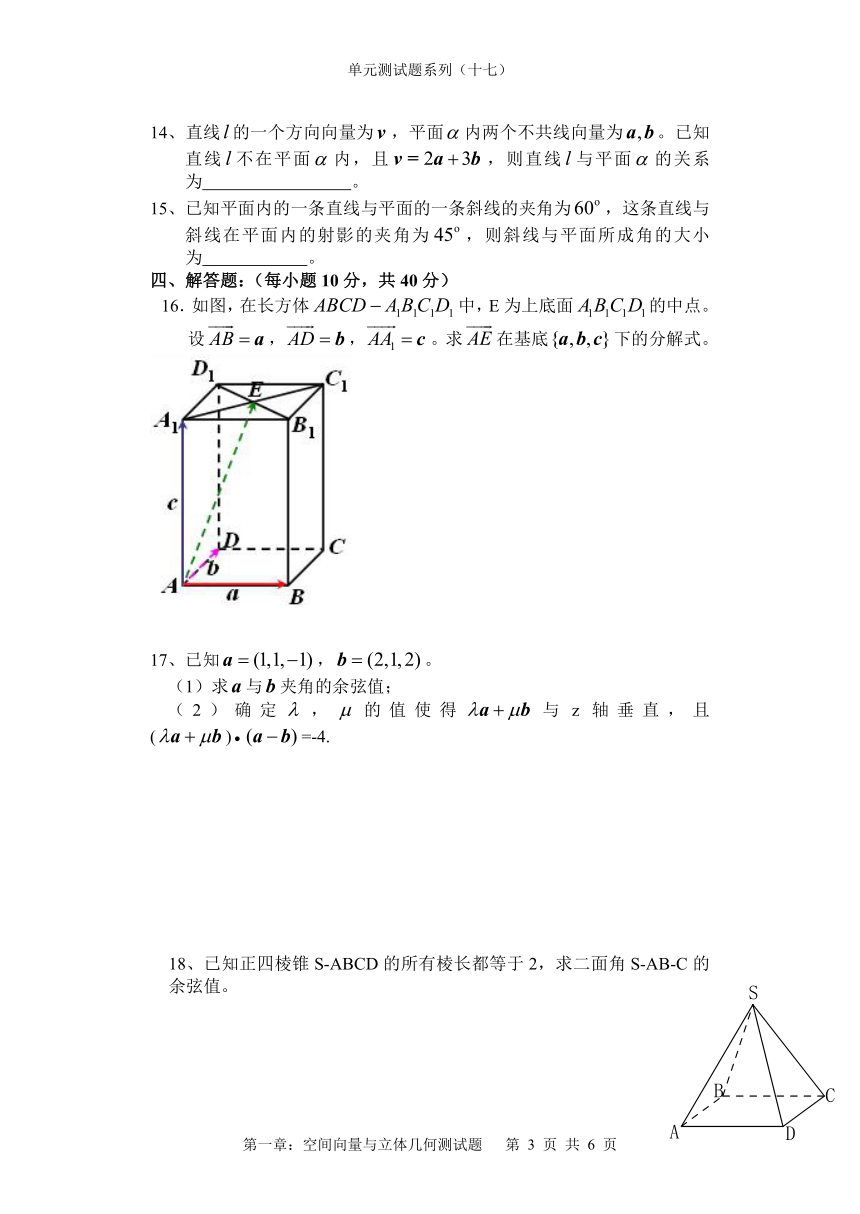
16.如图,在长方体中,E为上底面的中点。设,,。求在基底下的分解式。
17、已知,。
(1)求与夹角的余弦值;
(2)确定,的值使得与z轴垂直,且()=-4.
18、已知正四棱锥S-ABCD的所有棱长都等于2,求二面角S-AB-C的余弦值。
19、如图,在正方体中,求直线与平面所成角的大小。
第一章:空间向量与立体几何测试题参考答案
一、单项选择题:(每小题4分,共40分)
题号
1
2
3
4
5
6
7
答案
A
A
B
D
A
A
C
二、多项选择题:
题号
8
9
10
答案
CD
CD
AC
三、填空题:(每小题5分,共20分)
11、0
12、
13、1或
14、平行
15、
三、解答题:(每小题10分,共40分)
16.如图,在长方体中,E为上底面的中心。设,,。求在基底下的分解式。
解:因为在长方体中,E为上底面的中心,所以,。
。因为,,,所以。
17、已知,。
(1)求与夹角的余弦值;
(2)确定,的值使得与z轴垂直,且()。
解:(1),,所以,
,。
。
(2),z轴的方向向量取。
因为与z轴垂直,所以。
。因为(),所以。
解得。
18、已知正四棱锥S-ABCD的所有棱长都等于2,求二面角S-AB-C的余弦值。
解:取AB的中点E,连接SE.∵SA=SB,∴SE⊥AB。
设S在面ABCD内的射影为O,连接OE.∵S-ABCD是正四棱锥,∴OE⊥AB.∠SEO为二面角S-AB-C的平面角。
∵正四棱锥S-ABCD的所有棱长都等于2,∴SE=,OE=1.∴cos∠SEO==.
二面角S-AB-C的余弦值为为.
19、如图,在正方体中,求直线与平面所成角的大小。
解:以D为原点,为轴,轴和轴的正方向,建立空间直角坐标系如图。设正方体的棱长为1,则,,。设平面的法向量为
,则。设,则。
设直线与平面所成角为,则。
。直线与平面所成角为。
PAGE
第一章:空间向量与立体几何测试题
第
5
页
共
6
页
第一章:空间向量与立体几何测试题
考试时间:80分钟,总分:100分
一、单项选择题:(每小题4分,共28分)
1.
长方体ABCD-A1B1C1D1中,化简(
)
。
A.
B.
C.
D.
2.已知=,=,若∥,则与的值分别
为(
)。
A、,
B、5,2
C、,
D、-5,-2
3.
已知正方体的棱长为1,且,,
,则
(
)
。B
A.1
B.2
C.-1
D.3
4、若平面的法向量为,直线的方向向量为,直线与平面的夹角为,则下列关系式中成立的是(
)。
A、
B、
C、
D、
5、若平面、的法向量分别为=(1,2,-2),=(-3,-6,6),则(
)。
A、∥
B、⊥
C、、相交但不垂直
D、都不正确
6、在正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么
直线AM和CN所成角的余弦值是(
)。
A、
B、
C、
D、
7、若直线的方向向量与平面的法向量的夹角等于120o,则直线与平面
所成的角等于(
)。
A、120o
B、60o
C、30o
D、以上均不正确
二、多项选择题:(每小题4分,共12分)
8.以下结论正确的有(
)。
A.对于任意向量,有=
B.已知两个非零向量,,在空间任取一点O,作=
,
=,则称作向量与向量的夹角
C.对于任意向量,总有||成立。
D.对于任意向量,总有⊥成立。
9、以下结论正确的有(
)。
A.如果∥,则存在唯一个实数,使
B.如果存在实数对,使成立,则向量一定共面
C.设{a,b,c}是空间向量的一个基底,若向量,同时,
则。
D.设{a,b,c}是空间向量的一个基底,如果a,b,c的模都为1,且两两互相垂直,则该基底叫单位正交基底。
10、若n1,n2分别是平面的法向量,且,,,则可以取的值为(
)。
A、1
B、-1
C、2
D、-2
注意:请将选择题答案填入下表:
题号
一、单项选择题
二、多项选择题
1
2
3
4
5
6
7
8
9
10
答案
三、填空题:(每小题4分,共20分)
11.已知正方体的棱长为1,且,,,则
。
12、已知四面体ABCD中,且,,,D为线段OA中点,E为线段BC的中点,则在基底{,,c}下的分解式为
。
13、已知a=(2
,4
,x),b=(2
,y
,2),若|a|=6且a⊥b,则x+y等于
。
14、直线的一个方向向量为,平面内两个不共线向量为。已知直线不在平面内,且,则直线与平面的关系为
。
15、已知平面内的一条直线与平面的一条斜线的夹角为,这条直线与斜线在平面内的射影的夹角为,则斜线与平面所成角的大小为
。
四、解答题:(每小题10分,共40分)
16.如图,在长方体中,E为上底面的中点。设,,。求在基底下的分解式。
17、已知,。
(1)求与夹角的余弦值;
(2)确定,的值使得与z轴垂直,且()=-4.
18、已知正四棱锥S-ABCD的所有棱长都等于2,求二面角S-AB-C的余弦值。
19、如图,在正方体中,求直线与平面所成角的大小。
第一章:空间向量与立体几何测试题参考答案
一、单项选择题:(每小题4分,共40分)
题号
1
2
3
4
5
6
7
答案
A
A
B
D
A
A
C
二、多项选择题:
题号
8
9
10
答案
CD
CD
AC
三、填空题:(每小题5分,共20分)
11、0
12、
13、1或
14、平行
15、
三、解答题:(每小题10分,共40分)
16.如图,在长方体中,E为上底面的中心。设,,。求在基底下的分解式。
解:因为在长方体中,E为上底面的中心,所以,。
。因为,,,所以。
17、已知,。
(1)求与夹角的余弦值;
(2)确定,的值使得与z轴垂直,且()。
解:(1),,所以,
,。
。
(2),z轴的方向向量取。
因为与z轴垂直,所以。
。因为(),所以。
解得。
18、已知正四棱锥S-ABCD的所有棱长都等于2,求二面角S-AB-C的余弦值。
解:取AB的中点E,连接SE.∵SA=SB,∴SE⊥AB。
设S在面ABCD内的射影为O,连接OE.∵S-ABCD是正四棱锥,∴OE⊥AB.∠SEO为二面角S-AB-C的平面角。
∵正四棱锥S-ABCD的所有棱长都等于2,∴SE=,OE=1.∴cos∠SEO==.
二面角S-AB-C的余弦值为为.
19、如图,在正方体中,求直线与平面所成角的大小。
解:以D为原点,为轴,轴和轴的正方向,建立空间直角坐标系如图。设正方体的棱长为1,则,,。设平面的法向量为
,则。设,则。
设直线与平面所成角为,则。
。直线与平面所成角为。
PAGE
第一章:空间向量与立体几何测试题
第
5
页
共
6
页
