2021-2022学年人教版八年级数学上册12.3角的平分线的性质 同步能力提升训练(word版、含解析)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册12.3角的平分线的性质 同步能力提升训练(word版、含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 283.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 15:59:06 | ||
图片预览




文档简介
2021-2022年人教版八年级数学上册《12.3角的平分线的性质》同步能力提升训练(附答案)
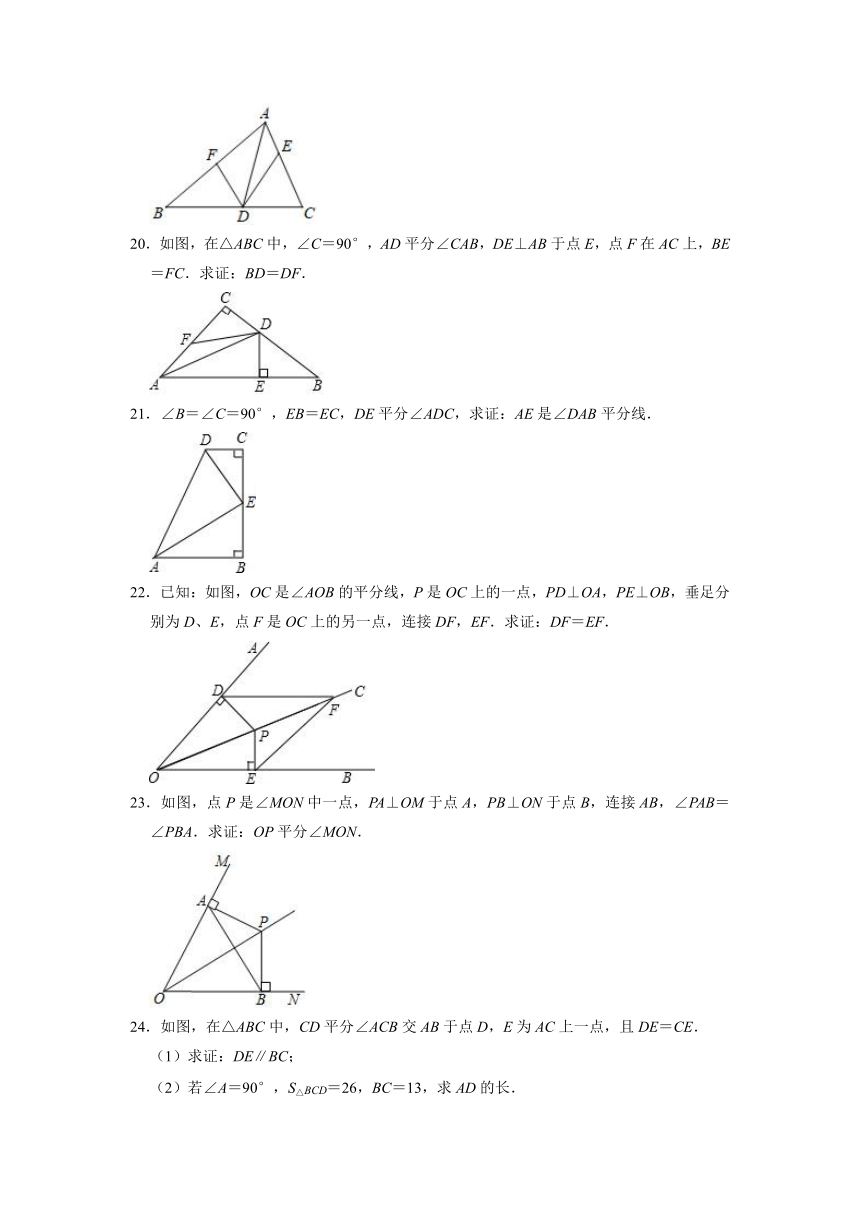
1.如图,P是∠BAC的平分线AD上的一点,PE⊥AC于点E.已知PE=4,则点P到AB的距离是( )
A.5
B.4
C.3
D.无法确定
2.△ABC的三边AB、BC、CA长分别是15、20、25,其三条角平分线相交于O点,将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )
A.1:1:1
B.1:2:3
C.2:3:4
D.3:4:5
3.如图,AI、BI、CI分别平分∠BAC、∠ABC、∠ACB,ID⊥BC,△ABC的周长为18,ID=3,则△ABC的面积为( )
A.18
B.30
C.24
D.27
4.如图,三条直线表示三条相互交叉的道路,现要建一个货物中转站,使它到三条道路的距离相等,则可选择的地址有( )
A.一处
B.二处
C.三处
D.四处
5.如图,在Rt△ABC中,BD是∠ABC的平分线,DE⊥AB,垂足是E.若AC=5,DE=2,则AD为( )
A.4
B.3
C.2
D.1
6.如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P,DP=5,若点Q是射线OB上一点,OQ=3,则△ODQ的面积是( )
A.6.5
B.7.5
C.8
D.10
7.如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,则判定图中两三角形全等的条件是( )
A.SAS
B.ASA
C.AAS
D.SSS
8.如图,△ABC中,∠ABC的外角平分线BD与∠ACB的外角平分线CE相交于点P,若点P到AC的距离为4,则点P到AB的距离为
,推理出结论所用到的理论依据是
.
9.如图,△ABC中,∠ABC和∠ACB的平分线交于点P,若点P到BC的距离是2,△ABC的周长是10,则△ABC的面积是
.
10.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABD的面积是12cm2,AB=8cm,则DF=
.
11.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若BC=7,DE=3,则BD的长为
.
12.如图,四边形ABCD中,∠A=90°,AD=3,连接BD,BD⊥CD,垂足为D,∠ADB=∠C,点P是边BC上的一动点,则DP的最小值是
.
13.如图BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于点F,连接AD.
(1)求证:AD平分∠GAC;
(2)若AB=AD,请判断△ABC的形状,并证明你的结论.
14.如图,已知AC平分∠BAD,CE⊥AB,CD⊥AD,点E,D分别为垂足,CF=CB.求证:BE=FD.
15.如图,AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,BD=CD.求证:EB=FC.
16.如图,△ABE中,∠E=90°,AC是∠BAE的角平分线.
(1)若∠B=40°,求∠BAC的度数;
(2)若D是BC的中点,△ADC的面积为16,AE=8,求BC的长.
17.如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8,若S△ABC=28,求DE的长.
18.如图,在△ABC中,AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,D是BC的中点,证明:∠B=∠C.
19.如图,已知点D、E、F分别是△ABC的三边上的点,CE=BF,且△DCE的面积与△DBF的面积相等.求证:AD平分∠BAC.
20.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,点F在AC上,BE=FC.求证:BD=DF.
21.∠B=∠C=90°,EB=EC,DE平分∠ADC,求证:AE是∠DAB平分线.
22.已知:如图,OC是∠AOB的平分线,P是OC上的一点,PD⊥OA,PE⊥OB,垂足分别为D、E,点F是OC上的另一点,连接DF,EF.求证:DF=EF.
23.如图,点P是∠MON中一点,PA⊥OM于点A,PB⊥ON于点B,连接AB,∠PAB=∠PBA.求证:OP平分∠MON.
24.如图,在△ABC中,CD平分∠ACB交AB于点D,E为AC上一点,且DE=CE.
(1)求证:DE∥BC;
(2)若∠A=90°,S△BCD=26,BC=13,求AD的长.
参考答案
1.解:∵P是∠BAC的平分线AD上的一点,PE⊥AC于点E.已知PE=4,
∴点P到AB的距离=PE=4,
故选:B.
2.解:过点O作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,
∵三条角平分线相交于O点,
∴OE=OF=OD,
∵△ABC的三边AB、BC、CA长分别是15、20、25,
∴S△ABO:S△BCO:S△CAO= AB OE: BC OF: AC OD=AB:BC:AC=3:4:5,
故选:D.
3.解:如图,过点I作IE⊥AB于E,IF⊥AC于F,
∵∠ABC、∠ACB的平分线,ID⊥BC,
∴ID=IE,ID=IE,
∴ID=IE=IF=3,
∵△ABC的周长为18,
∴△ABC的面积=(AB+BC+AC)×3=×18×3=27.
故选:D.
4.解:如图,
可选择的地址有四处.
故选:D.
5.解:∵BD是∠ABC平分线,DE⊥AB,∠C=90°,
∴DE=CD=2,
∵AC=5,
∴AD=AC﹣CD=5﹣2=3,
故选:B.
6.解:作DE⊥OB于E,如图,
∵OC是∠AOB的角平分线,DP⊥OA,DE⊥OB,
∴DE=DP=5,
∵OQ=3,
∴,
故选:B.
7.解:如图,由作图可知,OA=OB=CE=EF,BA=CF.
在△AOB和△CEF中,
,
∴△AOB≌△CEF(SSS),
故选:D.
8.解:如图,过点P作PF⊥AC于F,PG⊥BC于G,PH⊥AB于H,
∵∠ABC的外角平分线BD与∠ACB的外角平分线CE相交于点P,
∴PF=PG=4,PG=PH,
∴PF=PG=PH=4.
推理出结论所用到的理论依据是角平分线的性质,
故答案为:4,角平分线的性质.
9.解:连接AP,过P作PD⊥BC,PE⊥AB,PF⊥AC,
∵角平分线BP与CP相交于点P,
∴AP是∠BAC的平分线,
∴PD=PE=PF,
∴S△ABC=S△ABP+S△BCP+S△ACP=(AB+BC+AC) PD=×10×2=10.
故答案为10.
10.解:∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∵S△ABD=×AB×DE=DE=12cm2,
∴DE=3(cm).
∴DF=DE=3cm,
故答案为3cm.
11.解:∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴CD=DE,
∵DE=3,
∴CD=3,
∴BD=BC﹣CD=7﹣3=4.
故答案为:4.
12.解:由垂线段最短可得DP⊥BC时,DP有最小值,
∵∠A+∠ADB+∠ABD=180°,∠BDC+∠C+∠DBC=180°,∠A=90°,
∴∠ABD=∠DBC,
∴DP=AD,
∵AD=3,
∴DP的最小值为3.
故答案为3.
13.(1)证明:过点D作DN⊥BA,DK⊥AC,DM⊥BC,垂足分别为点N、K、M.
∵BD、CD分别平分∠EBA、∠ECA,DN⊥BA,DK⊥AC,DM⊥BC,
∴DM=DN=DK,
∴AD平分∠GAC,∠ABD=∠DBC,
∴∠GAD=∠DAC,
∴AD平分∠GAC.
(2)解:△ABC是等腰三角形,
证明:∵AB=AD,
∴∠ABD=∠ADB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠CBD,
∴AD∥BC,
∴∠GAD=∠ABC,∠DAC=∠ACB,
∵AD平分∠GAC,
∴∠GAD=∠CAD,
∴∠ABC=∠ACB,
∴△ABC是等腰三角形.
14.证明:∵AC平分∠BAD,CE⊥AB,CD⊥AD,
∴CD=CE,
在Rt△CBE和Rt△CFD中,
,
∴Rt△CBE≌Rt△CFD(HL),
∴BE=FD.
15.证明:∵AD是∠BAC的角平分线,
∴∠BAD=∠CAD,
又∵DE⊥AB,DF⊥AC,
∴DE=DF,
又∵DE⊥AB,DF⊥AC,BD=CD,
在Rt△BDE与Rt△CDF中,
,
∴Rt△BDE≌Rt△CDF(HL),
∴EB=FC.
16.解:(1)∵∠B=40°,∠E=90°,
∴∠BAE=90° 40°=50°,
∵AC是∠BAE的角平分线,
∴∠BAC=∠BAE=25°;
(2)∵S△ADC=DC AE,
∴×DC×8=16,
∴DC=4,
∵D是BC的中点,
∴BC=2CD=8.
17.解:∵BD平分∠ABC交AC于点D,DE⊥AB,DF⊥BC,
∴DE=DF,
∵AB=6,BC=8,S△ABC=28,
∴S△ABC=S△ABD+S△BCD=AB DE+BC DF=DE (AB+BC)=28,
即DE(6+8)=28,
∴DE=4.
18.证明:∵D是BC的中点,
∴BD=CD,
∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
在Rt△BED和Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴∠B=∠C.
19.证明:过D作DM⊥AB于M,DN⊥AC于N,
∵△DCE的面积与△DBF的面积相等,
∴=,
∵CE=BF,
∴DM=DN,
∴点D在∠BAC的平分线上,
又∵A点也在∠BAC的平分线上,
∴AD平分∠BAC.
20.证明:∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴DC=DE,
在△DCF和△DEB中,,
∴△DCF≌△DEB,(SAS),
∴BD=DF.
21.证明:如图,过点E作EF⊥AD于F,
∵DE平分∠ADC,∠C=90°,
∴EC=EF,
∵EB=EC,
∴EF=BE,
又∵∠B=90°,
∴EB⊥AB,
∵EF⊥AD,
∴AE是∠DAB平分线.
22.证明:∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,
∴PD=PE,
在Rt△OPD和Rt△OPE中,,
∴Rt△OPD≌Rt△OPE(HL),
∴OD=OE,
∵OC是∠AOB的平分线,
∴∠DOF=∠EOF,
在△ODF和△OEF中,,
∴△ODF≌△OEF(SAS),
∴DF=EF.
23.证明:∵∠PAB=∠PBA,
∴PA=PB,
∵PA⊥OM于点A,PB⊥ON于点B,
∴P点在∠MON的平分线上,
∴OP平分∠MON.
24.解:(1)∵CD平分∠ACB,
∴∠ECD=∠BCD,
又∵DE=CE,
∴∠ECD=∠EDC,
∴∠BCD=∠CDE,
∴DE∥BC;
(2)如图,过D作DF⊥BC于F,
∵∠A=90°,CD平分∠ACB,
∴AD=FD,
∵S△BCD=26,BC=13,
∴×13×DF=26,
∴DF=4,
∴AD=4.
1.如图,P是∠BAC的平分线AD上的一点,PE⊥AC于点E.已知PE=4,则点P到AB的距离是( )
A.5
B.4
C.3
D.无法确定
2.△ABC的三边AB、BC、CA长分别是15、20、25,其三条角平分线相交于O点,将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )
A.1:1:1
B.1:2:3
C.2:3:4
D.3:4:5
3.如图,AI、BI、CI分别平分∠BAC、∠ABC、∠ACB,ID⊥BC,△ABC的周长为18,ID=3,则△ABC的面积为( )
A.18
B.30
C.24
D.27
4.如图,三条直线表示三条相互交叉的道路,现要建一个货物中转站,使它到三条道路的距离相等,则可选择的地址有( )
A.一处
B.二处
C.三处
D.四处
5.如图,在Rt△ABC中,BD是∠ABC的平分线,DE⊥AB,垂足是E.若AC=5,DE=2,则AD为( )
A.4
B.3
C.2
D.1
6.如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P,DP=5,若点Q是射线OB上一点,OQ=3,则△ODQ的面积是( )
A.6.5
B.7.5
C.8
D.10
7.如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,则判定图中两三角形全等的条件是( )
A.SAS
B.ASA
C.AAS
D.SSS
8.如图,△ABC中,∠ABC的外角平分线BD与∠ACB的外角平分线CE相交于点P,若点P到AC的距离为4,则点P到AB的距离为
,推理出结论所用到的理论依据是
.
9.如图,△ABC中,∠ABC和∠ACB的平分线交于点P,若点P到BC的距离是2,△ABC的周长是10,则△ABC的面积是
.
10.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABD的面积是12cm2,AB=8cm,则DF=
.
11.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若BC=7,DE=3,则BD的长为
.
12.如图,四边形ABCD中,∠A=90°,AD=3,连接BD,BD⊥CD,垂足为D,∠ADB=∠C,点P是边BC上的一动点,则DP的最小值是
.
13.如图BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于点F,连接AD.
(1)求证:AD平分∠GAC;
(2)若AB=AD,请判断△ABC的形状,并证明你的结论.
14.如图,已知AC平分∠BAD,CE⊥AB,CD⊥AD,点E,D分别为垂足,CF=CB.求证:BE=FD.
15.如图,AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,BD=CD.求证:EB=FC.
16.如图,△ABE中,∠E=90°,AC是∠BAE的角平分线.
(1)若∠B=40°,求∠BAC的度数;
(2)若D是BC的中点,△ADC的面积为16,AE=8,求BC的长.
17.如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8,若S△ABC=28,求DE的长.
18.如图,在△ABC中,AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,D是BC的中点,证明:∠B=∠C.
19.如图,已知点D、E、F分别是△ABC的三边上的点,CE=BF,且△DCE的面积与△DBF的面积相等.求证:AD平分∠BAC.
20.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,点F在AC上,BE=FC.求证:BD=DF.
21.∠B=∠C=90°,EB=EC,DE平分∠ADC,求证:AE是∠DAB平分线.
22.已知:如图,OC是∠AOB的平分线,P是OC上的一点,PD⊥OA,PE⊥OB,垂足分别为D、E,点F是OC上的另一点,连接DF,EF.求证:DF=EF.
23.如图,点P是∠MON中一点,PA⊥OM于点A,PB⊥ON于点B,连接AB,∠PAB=∠PBA.求证:OP平分∠MON.
24.如图,在△ABC中,CD平分∠ACB交AB于点D,E为AC上一点,且DE=CE.
(1)求证:DE∥BC;
(2)若∠A=90°,S△BCD=26,BC=13,求AD的长.
参考答案
1.解:∵P是∠BAC的平分线AD上的一点,PE⊥AC于点E.已知PE=4,
∴点P到AB的距离=PE=4,
故选:B.
2.解:过点O作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,
∵三条角平分线相交于O点,
∴OE=OF=OD,
∵△ABC的三边AB、BC、CA长分别是15、20、25,
∴S△ABO:S△BCO:S△CAO= AB OE: BC OF: AC OD=AB:BC:AC=3:4:5,
故选:D.
3.解:如图,过点I作IE⊥AB于E,IF⊥AC于F,
∵∠ABC、∠ACB的平分线,ID⊥BC,
∴ID=IE,ID=IE,
∴ID=IE=IF=3,
∵△ABC的周长为18,
∴△ABC的面积=(AB+BC+AC)×3=×18×3=27.
故选:D.
4.解:如图,
可选择的地址有四处.
故选:D.
5.解:∵BD是∠ABC平分线,DE⊥AB,∠C=90°,
∴DE=CD=2,
∵AC=5,
∴AD=AC﹣CD=5﹣2=3,
故选:B.
6.解:作DE⊥OB于E,如图,
∵OC是∠AOB的角平分线,DP⊥OA,DE⊥OB,
∴DE=DP=5,
∵OQ=3,
∴,
故选:B.
7.解:如图,由作图可知,OA=OB=CE=EF,BA=CF.
在△AOB和△CEF中,
,
∴△AOB≌△CEF(SSS),
故选:D.
8.解:如图,过点P作PF⊥AC于F,PG⊥BC于G,PH⊥AB于H,
∵∠ABC的外角平分线BD与∠ACB的外角平分线CE相交于点P,
∴PF=PG=4,PG=PH,
∴PF=PG=PH=4.
推理出结论所用到的理论依据是角平分线的性质,
故答案为:4,角平分线的性质.
9.解:连接AP,过P作PD⊥BC,PE⊥AB,PF⊥AC,
∵角平分线BP与CP相交于点P,
∴AP是∠BAC的平分线,
∴PD=PE=PF,
∴S△ABC=S△ABP+S△BCP+S△ACP=(AB+BC+AC) PD=×10×2=10.
故答案为10.
10.解:∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∵S△ABD=×AB×DE=DE=12cm2,
∴DE=3(cm).
∴DF=DE=3cm,
故答案为3cm.
11.解:∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴CD=DE,
∵DE=3,
∴CD=3,
∴BD=BC﹣CD=7﹣3=4.
故答案为:4.
12.解:由垂线段最短可得DP⊥BC时,DP有最小值,
∵∠A+∠ADB+∠ABD=180°,∠BDC+∠C+∠DBC=180°,∠A=90°,
∴∠ABD=∠DBC,
∴DP=AD,
∵AD=3,
∴DP的最小值为3.
故答案为3.
13.(1)证明:过点D作DN⊥BA,DK⊥AC,DM⊥BC,垂足分别为点N、K、M.
∵BD、CD分别平分∠EBA、∠ECA,DN⊥BA,DK⊥AC,DM⊥BC,
∴DM=DN=DK,
∴AD平分∠GAC,∠ABD=∠DBC,
∴∠GAD=∠DAC,
∴AD平分∠GAC.
(2)解:△ABC是等腰三角形,
证明:∵AB=AD,
∴∠ABD=∠ADB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠CBD,
∴AD∥BC,
∴∠GAD=∠ABC,∠DAC=∠ACB,
∵AD平分∠GAC,
∴∠GAD=∠CAD,
∴∠ABC=∠ACB,
∴△ABC是等腰三角形.
14.证明:∵AC平分∠BAD,CE⊥AB,CD⊥AD,
∴CD=CE,
在Rt△CBE和Rt△CFD中,
,
∴Rt△CBE≌Rt△CFD(HL),
∴BE=FD.
15.证明:∵AD是∠BAC的角平分线,
∴∠BAD=∠CAD,
又∵DE⊥AB,DF⊥AC,
∴DE=DF,
又∵DE⊥AB,DF⊥AC,BD=CD,
在Rt△BDE与Rt△CDF中,
,
∴Rt△BDE≌Rt△CDF(HL),
∴EB=FC.
16.解:(1)∵∠B=40°,∠E=90°,
∴∠BAE=90° 40°=50°,
∵AC是∠BAE的角平分线,
∴∠BAC=∠BAE=25°;
(2)∵S△ADC=DC AE,
∴×DC×8=16,
∴DC=4,
∵D是BC的中点,
∴BC=2CD=8.
17.解:∵BD平分∠ABC交AC于点D,DE⊥AB,DF⊥BC,
∴DE=DF,
∵AB=6,BC=8,S△ABC=28,
∴S△ABC=S△ABD+S△BCD=AB DE+BC DF=DE (AB+BC)=28,
即DE(6+8)=28,
∴DE=4.
18.证明:∵D是BC的中点,
∴BD=CD,
∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
在Rt△BED和Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴∠B=∠C.
19.证明:过D作DM⊥AB于M,DN⊥AC于N,
∵△DCE的面积与△DBF的面积相等,
∴=,
∵CE=BF,
∴DM=DN,
∴点D在∠BAC的平分线上,
又∵A点也在∠BAC的平分线上,
∴AD平分∠BAC.
20.证明:∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴DC=DE,
在△DCF和△DEB中,,
∴△DCF≌△DEB,(SAS),
∴BD=DF.
21.证明:如图,过点E作EF⊥AD于F,
∵DE平分∠ADC,∠C=90°,
∴EC=EF,
∵EB=EC,
∴EF=BE,
又∵∠B=90°,
∴EB⊥AB,
∵EF⊥AD,
∴AE是∠DAB平分线.
22.证明:∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,
∴PD=PE,
在Rt△OPD和Rt△OPE中,,
∴Rt△OPD≌Rt△OPE(HL),
∴OD=OE,
∵OC是∠AOB的平分线,
∴∠DOF=∠EOF,
在△ODF和△OEF中,,
∴△ODF≌△OEF(SAS),
∴DF=EF.
23.证明:∵∠PAB=∠PBA,
∴PA=PB,
∵PA⊥OM于点A,PB⊥ON于点B,
∴P点在∠MON的平分线上,
∴OP平分∠MON.
24.解:(1)∵CD平分∠ACB,
∴∠ECD=∠BCD,
又∵DE=CE,
∴∠ECD=∠EDC,
∴∠BCD=∠CDE,
∴DE∥BC;
(2)如图,过D作DF⊥BC于F,
∵∠A=90°,CD平分∠ACB,
∴AD=FD,
∵S△BCD=26,BC=13,
∴×13×DF=26,
∴DF=4,
∴AD=4.
