苏科版八年级数学上册 2.5 等腰三角形的轴对称性(共21张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 2.5 等腰三角形的轴对称性(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
2.5
等腰三角形
的轴对称性㈠
A
B
C
A
B
C
D
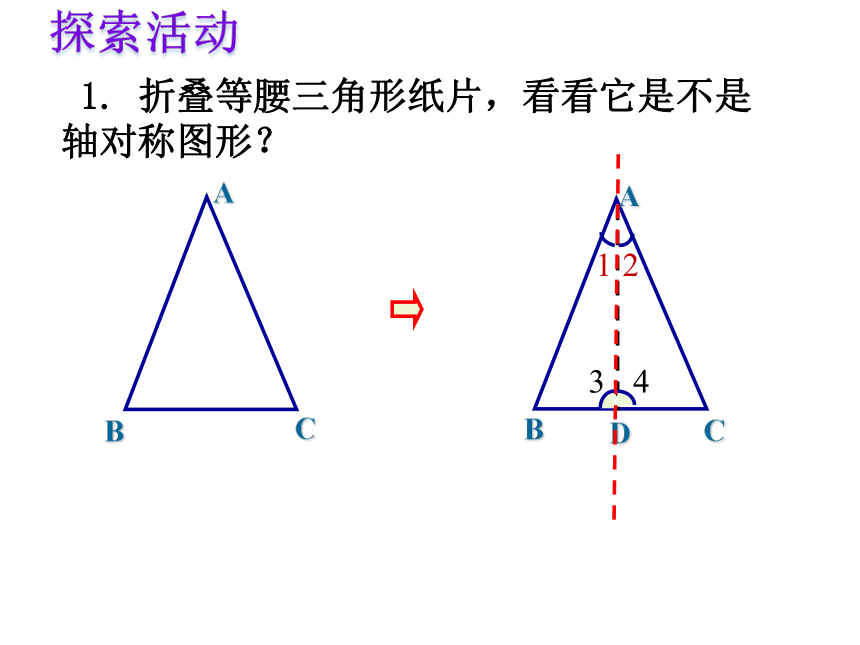
1.
折叠等腰三角形纸片,看看它是不是
轴对称图形?
1
2
3
4
2.猜想:等腰三角形有哪些性质?
①等腰三角形的两个底角相等
②等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合
A
B
C
D
3.你能证明这两个猜想吗?
已知:AB=AC
求证:∠B=∠C
作角平分线
作高
作中线
A
B
C
则有∠1=∠2,
D
1
2
在△ABD和△ACD中,
证明:过点A作AD平分∠BAC交BC于D.
AB=AC,
∠1=∠2,
AD=AD
∴
△ABD≌
△ACD
(SAS)
∴
∠B=∠C
∴
BD=CD,
∠3=∠4=90°
验证猜想
3
4
作顶角的平分线
A
B
C
则有∠3=∠4=90°
D
1
2
在RT△ABD和RT△ACD中,
证明:过点A作AD
⊥BC于D
AB=AC
AD=AD
∴RT△ABD≌
RT△ACD
(HL)
∴
∠B=∠C
∴
BD=CD,
∠1=∠2
验证猜想
3
4
∟
∟
作底边上的高
A
B
C
则有BD=CD
D
1
2
在△ABD和△ACD中,
证明:取BC中点D,连接AD
AB=AC
AD=AD
(SSS)
∴
∠B=∠C
∴
∠1=∠2,
∠3=∠4=90°
验证猜想
3
4
作底边上的中线
BD=CD
∴△ABD≌
△ACD
2.猜想:等腰三角形有哪些性质?
①等腰三角形的两个底角相等
②等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合
A
B
C
D
3.验证:你能证明你的猜想吗?
已知:AB=AC
求证:∠B=∠C
作角平分线
作高
作中线
作辅助线AD!
∵
AB=AC,
BD=CD,
∴_______________
∠1=∠2,AD⊥BC
∵
AB=AC,
AD⊥BC
∴_______________
∵
AB=AC,∠1=∠2
∴
______________
AD⊥BC,BD=CD
∠1=∠2,
BD=CD
等腰三角形的性质定理
总结归纳:
①等腰三角形的两个底角相等
(“等边对等角”)
②等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合
(“三线合一”)
∵AB=AC
∴_________
∠B=∠C
符号语言:
1.用直尺和圆规作等腰三角形ABC,
使底边BC=a,高AD=h.
A
B
C
∟
D
h
a
2.(1)等腰三角形的顶角是80度,则底角是____度。
(2)
等腰三角形中有一个角是80度,则其余两个角的度数是_________
顶角?底角?
500
500、500
或
200、800
分类讨论
800
500
200
800
800
500
3、如图,在△ABC中,AB=AC,点D在CB上,且AD=BD,
求证:
∠ADB=∠BAC.
A
B
C
D
如图,在△ABC中,AB=AC,点D为BC的中点,DE⊥AB,DF⊥AC,
证明:DE=DF
∴DE=DF
(
?)
证明:连接AD
∵
∵
AB=AC,D为BC中点
∴
∠BAD=∠CAD
(
?)
即
D在∠BAD的平分线上
∵
DE⊥AB于E
,DF⊥AC于F
方法二:利用△ABD
和△ACD面积相等
1
2
轴对称图形
两个底角相等,简称“等边对等角”
顶角平分线、底边上的中线、和底边上的高互相重合,简称“三线合
一”
数学思想及方法:
常用的辅助线:作“三线”
分类讨论
转化思想
1.在△ABC中,AB=AC
(1)如果两边长为4和5,则周长为______
(2)如果有一个角等于120°,那么∠A=___,∠B=___,∠C=___
A
B
C
(3)如果有一个角等于50°,那么∠A=______
2.如图:△ABC中,AB=AC,AD⊥BC,∠BAC=110°,
求∠B和∠1的度数.
如图:△ABC中,AB=AC,AD=AE
试说明:BE=CD
E
D
C
B
A
【思考题】
2.5
等腰三角形
的轴对称性㈠
A
B
C
A
B
C
D
1.
折叠等腰三角形纸片,看看它是不是
轴对称图形?
1
2
3
4
2.猜想:等腰三角形有哪些性质?
①等腰三角形的两个底角相等
②等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合
A
B
C
D
3.你能证明这两个猜想吗?
已知:AB=AC
求证:∠B=∠C
作角平分线
作高
作中线
A
B
C
则有∠1=∠2,
D
1
2
在△ABD和△ACD中,
证明:过点A作AD平分∠BAC交BC于D.
AB=AC,
∠1=∠2,
AD=AD
∴
△ABD≌
△ACD
(SAS)
∴
∠B=∠C
∴
BD=CD,
∠3=∠4=90°
验证猜想
3
4
作顶角的平分线
A
B
C
则有∠3=∠4=90°
D
1
2
在RT△ABD和RT△ACD中,
证明:过点A作AD
⊥BC于D
AB=AC
AD=AD
∴RT△ABD≌
RT△ACD
(HL)
∴
∠B=∠C
∴
BD=CD,
∠1=∠2
验证猜想
3
4
∟
∟
作底边上的高
A
B
C
则有BD=CD
D
1
2
在△ABD和△ACD中,
证明:取BC中点D,连接AD
AB=AC
AD=AD
(SSS)
∴
∠B=∠C
∴
∠1=∠2,
∠3=∠4=90°
验证猜想
3
4
作底边上的中线
BD=CD
∴△ABD≌
△ACD
2.猜想:等腰三角形有哪些性质?
①等腰三角形的两个底角相等
②等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合
A
B
C
D
3.验证:你能证明你的猜想吗?
已知:AB=AC
求证:∠B=∠C
作角平分线
作高
作中线
作辅助线AD!
∵
AB=AC,
BD=CD,
∴_______________
∠1=∠2,AD⊥BC
∵
AB=AC,
AD⊥BC
∴_______________
∵
AB=AC,∠1=∠2
∴
______________
AD⊥BC,BD=CD
∠1=∠2,
BD=CD
等腰三角形的性质定理
总结归纳:
①等腰三角形的两个底角相等
(“等边对等角”)
②等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合
(“三线合一”)
∵AB=AC
∴_________
∠B=∠C
符号语言:
1.用直尺和圆规作等腰三角形ABC,
使底边BC=a,高AD=h.
A
B
C
∟
D
h
a
2.(1)等腰三角形的顶角是80度,则底角是____度。
(2)
等腰三角形中有一个角是80度,则其余两个角的度数是_________
顶角?底角?
500
500、500
或
200、800
分类讨论
800
500
200
800
800
500
3、如图,在△ABC中,AB=AC,点D在CB上,且AD=BD,
求证:
∠ADB=∠BAC.
A
B
C
D
如图,在△ABC中,AB=AC,点D为BC的中点,DE⊥AB,DF⊥AC,
证明:DE=DF
∴DE=DF
(
?)
证明:连接AD
∵
∵
AB=AC,D为BC中点
∴
∠BAD=∠CAD
(
?)
即
D在∠BAD的平分线上
∵
DE⊥AB于E
,DF⊥AC于F
方法二:利用△ABD
和△ACD面积相等
1
2
轴对称图形
两个底角相等,简称“等边对等角”
顶角平分线、底边上的中线、和底边上的高互相重合,简称“三线合
一”
数学思想及方法:
常用的辅助线:作“三线”
分类讨论
转化思想
1.在△ABC中,AB=AC
(1)如果两边长为4和5,则周长为______
(2)如果有一个角等于120°,那么∠A=___,∠B=___,∠C=___
A
B
C
(3)如果有一个角等于50°,那么∠A=______
2.如图:△ABC中,AB=AC,AD⊥BC,∠BAC=110°,
求∠B和∠1的度数.
如图:△ABC中,AB=AC,AD=AE
试说明:BE=CD
E
D
C
B
A
【思考题】
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
