苏科版八年级数学上册 3.3 勾股定理的简单应用(共12张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 3.3 勾股定理的简单应用(共12张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 09:22:10 | ||
图片预览



文档简介
(共12张PPT)
勾股定理的应用
“匆忙”的人们自己劈开一条小道,请用数学知识解释其中的原因?
A
C
B
3米
5米
?
B
A
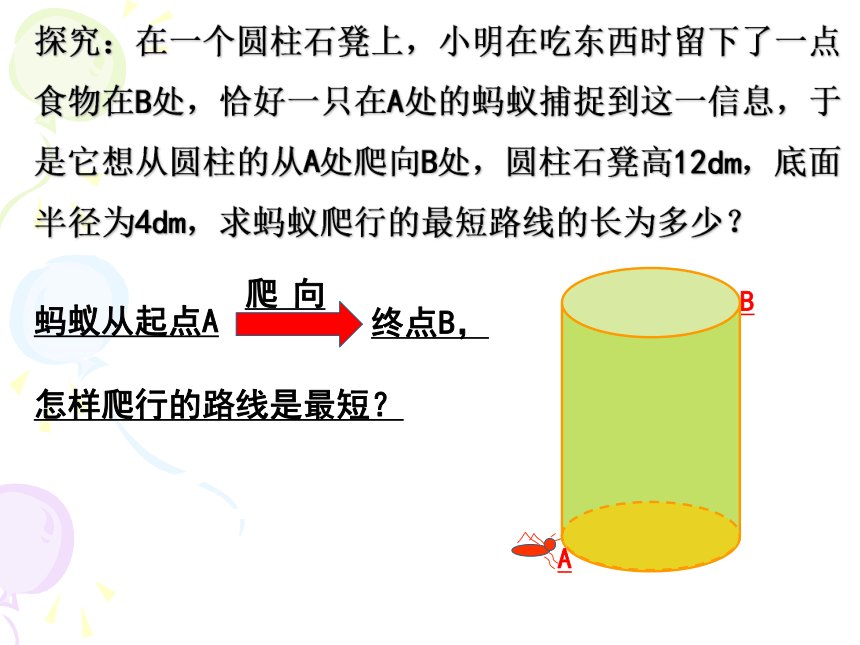
探究:在一个圆柱石凳上,小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想从圆柱的从A处爬向B处,圆柱石凳高12dm,底面半径为4dm,求蚂蚁爬行的最短路线的长为多少?
蚂蚁从起点A
爬
向
终点B,
怎样爬行的路线是最短?
B
A
1、拿出你做的圆柱,以小组为单位,尝试
画出蚂蚁从起点A
终点B
:爬行的可能路线,
并讨论哪条路线可能最短,依据是什么?
探究
蚂蚁A→B的路线
B
A
d
A
B
C
A
B
B
A
O
C
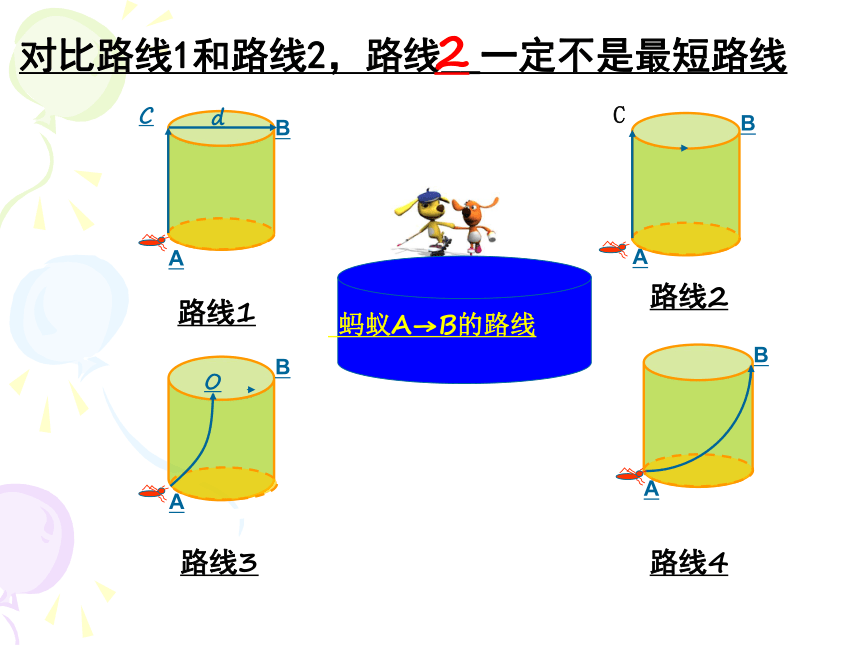
对比路线1和路线2,路线__一定不是最短路线
路线1
路线2
路线3
路线4
2
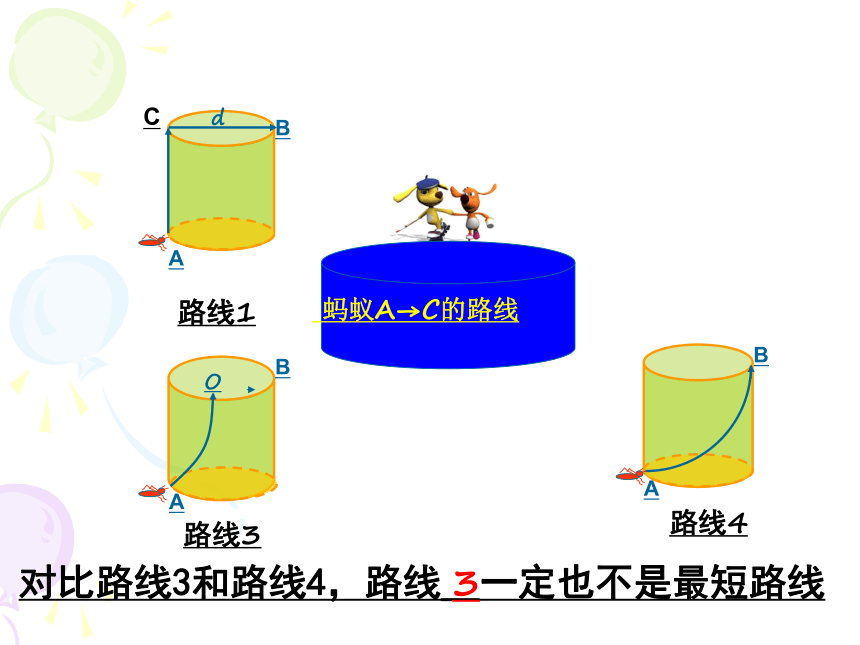
蚂蚁A→C的路线
B
A
d
A
B
B
A
O
C
对比路线3和路线4,路线__一定也不是最短路线
路线1
路线3
路线4
3
蚂蚁A→B的路线
B
A
d
A
B
C
路线1
路线4
对比路线1和路线4,能从图上观察哪条路线最短吗
A
A
B
B
C
d
侧面展开图
展开图
已知:圆柱石凳高12dm,底面圆半径为4dm,求蚂蚁爬行的最短路线的长为多少?(
取3)
已知:(1)圆柱石凳高5dm,底面圆半径为4dm;
(2)圆柱石凳高4dm,底面圆半径为4dm;
求蚂蚁爬行的最短路线是哪一条?长为多少?(
取3)
如何求解圆柱体图形中的最短路线问题?
1、
展
--------
立体→平面
起点
终点
路线
利用勾股定理
2、
找
--------
3、
连
--------
4、
算
--------
1、有一圆形油罐底面圆的周长为16m,高为7m,一只蚂蚁从距底面1m的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?
当堂检测
2、有一圆柱形油罐,底面周长是12米,高是5米,现从油罐底部A点环绕油罐建梯子,正好到点A的正上方点B,问梯子最短需多少米?
当堂检测
如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?
最短路线长为多少?
A
B
A1
B1
D
C
D1
C1
2
1
4
作业思考
勾股定理的应用
“匆忙”的人们自己劈开一条小道,请用数学知识解释其中的原因?
A
C
B
3米
5米
?
B
A
探究:在一个圆柱石凳上,小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想从圆柱的从A处爬向B处,圆柱石凳高12dm,底面半径为4dm,求蚂蚁爬行的最短路线的长为多少?
蚂蚁从起点A
爬
向
终点B,
怎样爬行的路线是最短?
B
A
1、拿出你做的圆柱,以小组为单位,尝试
画出蚂蚁从起点A
终点B
:爬行的可能路线,
并讨论哪条路线可能最短,依据是什么?
探究
蚂蚁A→B的路线
B
A
d
A
B
C
A
B
B
A
O
C
对比路线1和路线2,路线__一定不是最短路线
路线1
路线2
路线3
路线4
2
蚂蚁A→C的路线
B
A
d
A
B
B
A
O
C
对比路线3和路线4,路线__一定也不是最短路线
路线1
路线3
路线4
3
蚂蚁A→B的路线
B
A
d
A
B
C
路线1
路线4
对比路线1和路线4,能从图上观察哪条路线最短吗
A
A
B
B
C
d
侧面展开图
展开图
已知:圆柱石凳高12dm,底面圆半径为4dm,求蚂蚁爬行的最短路线的长为多少?(
取3)
已知:(1)圆柱石凳高5dm,底面圆半径为4dm;
(2)圆柱石凳高4dm,底面圆半径为4dm;
求蚂蚁爬行的最短路线是哪一条?长为多少?(
取3)
如何求解圆柱体图形中的最短路线问题?
1、
展
--------
立体→平面
起点
终点
路线
利用勾股定理
2、
找
--------
3、
连
--------
4、
算
--------
1、有一圆形油罐底面圆的周长为16m,高为7m,一只蚂蚁从距底面1m的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?
当堂检测
2、有一圆柱形油罐,底面周长是12米,高是5米,现从油罐底部A点环绕油罐建梯子,正好到点A的正上方点B,问梯子最短需多少米?
当堂检测
如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?
最短路线长为多少?
A
B
A1
B1
D
C
D1
C1
2
1
4
作业思考
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
