苏科版九年级数学上册 1.3 一元二次方程的根与系数的关系(共17张PPT)
文档属性
| 名称 | 苏科版九年级数学上册 1.3 一元二次方程的根与系数的关系(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
人物简介
韦达(1540-1603),法国数学家。年轻时学习法律当过律师,后从事政治活动,当过议会议员。在1595-1598年法国和西班牙的战争中,韦达利用自己精湛的数学方法,成功地破译了西班牙的军事密码,为法国赢得了战争的主动权。因为韦达立下赫赫战功,在之后他得到了更为重要的职位,比如法国检察官,法国最高律师等等。韦达从事数学研究只是出于爱好,然而他却完成了代数和三角学方面的很多著作。韦达是第一个有意识并系统地使用字母来表示已知数、未知数及其乘幂,带来了代数理论研究的重大进步。韦达研究方程根的多种有理变换,发现了n次方程根与系数的关系。
主要著作:《分析法入门》、《论方程的识别与修正》、《分析五章》、《应用于三角形的数学定律》等。由于韦达贡献卓著,因此,韦达被人们称为“现代代数的奠基人”,被尊称为“代数学之父”。
2.一元二次方程的求根公式是什么?
1.一元二次方程的一般形式是什么?
复
习
巩
固
1.3
一元二次方程的根与系数的关系
1.3
一元二次方程的根与系数的关系
新知探究
活动一
填表:探究一元二次方程的根与系数的关系
ax +bx+c=0
x -3x+2=0
x +3x+2=0
x -5x+6=0
x +5x+6=0
x -3x=0
1
2
-2
-1
2
-2
0
3
3
-3
3
2
-3
2
4
4
-5
6
3
0
观察并思考表格中方程两根的和及两根的积与系数的关系.
新知探究
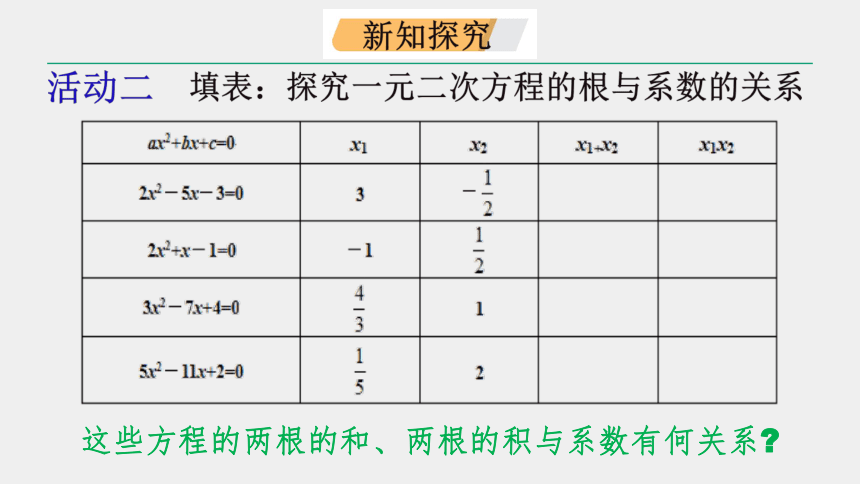
活动二
填表:探究一元二次方程的根与系数的关系
这些方程的两根的和、两根的积与系数有何关系
解释规律
你能解释刚才的发现吗?
一元二次方程
ax2+bx+c=0
(a≠0),如果b2-4ac≥0,它的两个根分别是x1、x2.
总结归纳
方程ax2+bx+c=0
(a≠0)的两个根是x1、x2,
,
.
这就是一元二次方程根与系数的关系,也叫韦达定理.
例题学习
例
1
求下列方程两根的和与两根的积:
(1)x2+2x-5=0;
(2)2x2+x=1.
友情提醒
在使用一元二次方程根与系数的关系时,应注意:
(1)不是一般式的要先化成一般式.
(3)当且仅当b2-4ac≥0时,才能应用根与系数的关系.
牛刀小试
1.口答出下列方程的两根的和与两根的积:
牛刀小试
2.下列结论是否正确?
(3)一元二次方程x2-3x+4=0的两个根之和为3.
旧题再现
思维拓展
归纳总结
求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和、两根之积的形式,再整体代入.
尝试交流
你能写出这个方程中被墨迹污染的一次项系数和常数项吗?
小明在一本课外读物中读到如下一段文字:
一元二次方程x2+
x
=0的两根是
和
.
变式训练
利用根与系数关系,写一个一元二次方程,使它的两个根分别为1,-4.
1.3
一元二次方程的根与系数的关系
课堂小结
通过这节课的学习,你有什么收获?
人物简介
韦达(1540-1603),法国数学家。年轻时学习法律当过律师,后从事政治活动,当过议会议员。在1595-1598年法国和西班牙的战争中,韦达利用自己精湛的数学方法,成功地破译了西班牙的军事密码,为法国赢得了战争的主动权。因为韦达立下赫赫战功,在之后他得到了更为重要的职位,比如法国检察官,法国最高律师等等。韦达从事数学研究只是出于爱好,然而他却完成了代数和三角学方面的很多著作。韦达是第一个有意识并系统地使用字母来表示已知数、未知数及其乘幂,带来了代数理论研究的重大进步。韦达研究方程根的多种有理变换,发现了n次方程根与系数的关系。
主要著作:《分析法入门》、《论方程的识别与修正》、《分析五章》、《应用于三角形的数学定律》等。由于韦达贡献卓著,因此,韦达被人们称为“现代代数的奠基人”,被尊称为“代数学之父”。
2.一元二次方程的求根公式是什么?
1.一元二次方程的一般形式是什么?
复
习
巩
固
1.3
一元二次方程的根与系数的关系
1.3
一元二次方程的根与系数的关系
新知探究
活动一
填表:探究一元二次方程的根与系数的关系
ax +bx+c=0
x -3x+2=0
x +3x+2=0
x -5x+6=0
x +5x+6=0
x -3x=0
1
2
-2
-1
2
-2
0
3
3
-3
3
2
-3
2
4
4
-5
6
3
0
观察并思考表格中方程两根的和及两根的积与系数的关系.
新知探究
活动二
填表:探究一元二次方程的根与系数的关系
这些方程的两根的和、两根的积与系数有何关系
解释规律
你能解释刚才的发现吗?
一元二次方程
ax2+bx+c=0
(a≠0),如果b2-4ac≥0,它的两个根分别是x1、x2.
总结归纳
方程ax2+bx+c=0
(a≠0)的两个根是x1、x2,
,
.
这就是一元二次方程根与系数的关系,也叫韦达定理.
例题学习
例
1
求下列方程两根的和与两根的积:
(1)x2+2x-5=0;
(2)2x2+x=1.
友情提醒
在使用一元二次方程根与系数的关系时,应注意:
(1)不是一般式的要先化成一般式.
(3)当且仅当b2-4ac≥0时,才能应用根与系数的关系.
牛刀小试
1.口答出下列方程的两根的和与两根的积:
牛刀小试
2.下列结论是否正确?
(3)一元二次方程x2-3x+4=0的两个根之和为3.
旧题再现
思维拓展
归纳总结
求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和、两根之积的形式,再整体代入.
尝试交流
你能写出这个方程中被墨迹污染的一次项系数和常数项吗?
小明在一本课外读物中读到如下一段文字:
一元二次方程x2+
x
=0的两根是
和
.
变式训练
利用根与系数关系,写一个一元二次方程,使它的两个根分别为1,-4.
1.3
一元二次方程的根与系数的关系
课堂小结
通过这节课的学习,你有什么收获?
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
