苏科版九年级数学上册 2.3 确定圆的条件(共22张PPT)
文档属性
| 名称 | 苏科版九年级数学上册 2.3 确定圆的条件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
初中数学九年级上册
(苏科版)
2.3
确定圆的条件
1、过一点可以作几条直线?
2、过几点可确定一条直线?
过几点可以确定一个圆呢?
回
顾
一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
要确定一个圆必须确定几个条件
情景创设
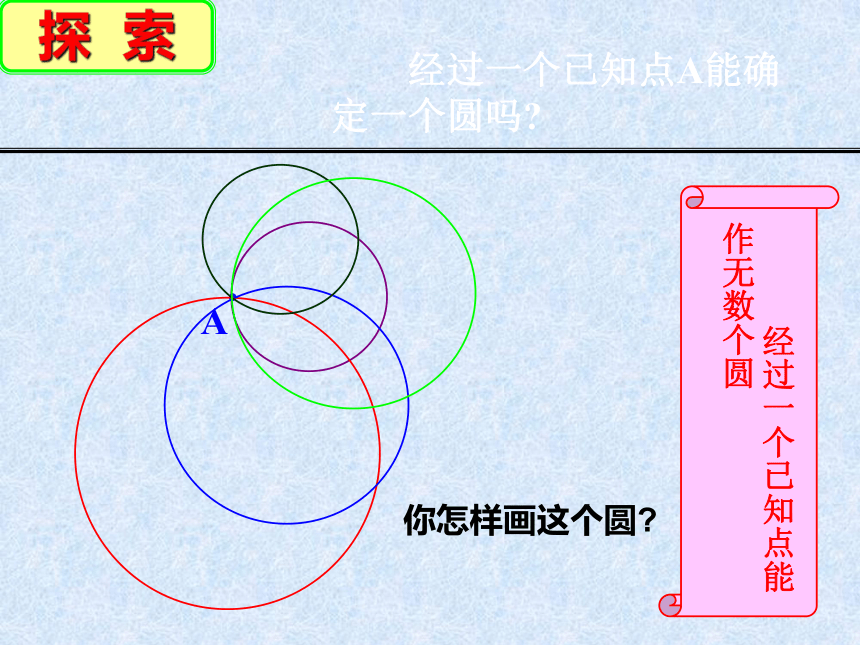
经过一个已知点A能确定一个圆吗
A
经过一个已知点能作无数个圆
你怎样画这个圆
探
索
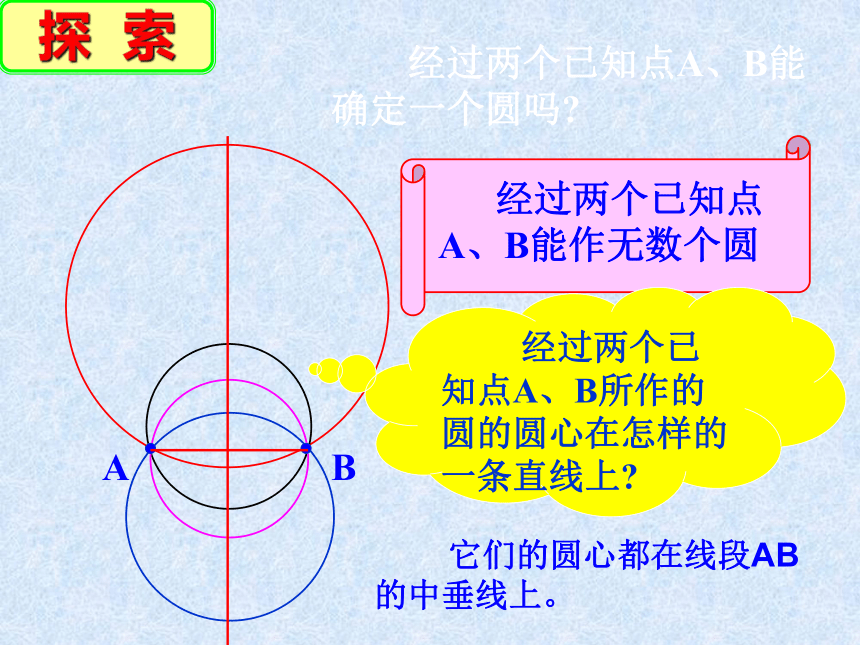
经过两个已知点A、B能确定一个圆吗
A
B
经过两个已知点A、B能作无数个圆
经过两个已知点A、B所作的圆的圆心在怎样的一条直线上
它们的圆心都在线段AB的中垂线上。
探
索
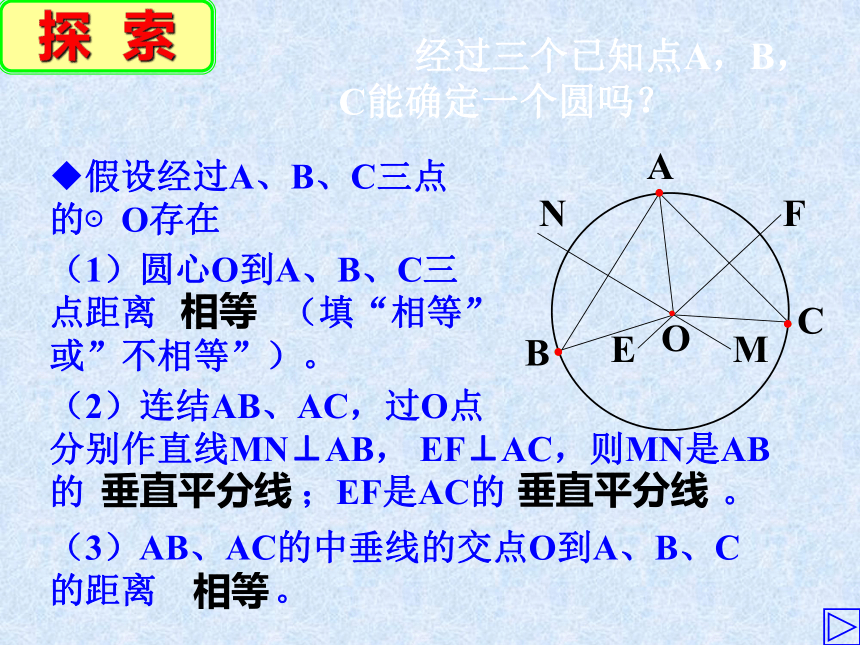
经过三个已知点A,B,C能确定一个圆吗?
假设经过A、B、C三点的⊙O存在
(1)圆心O到A、B、C三点距离
(填“相等”或”不相等”)。
(2)连结AB、AC,过O点
分别作直线MN⊥AB,
EF⊥AC,则MN是AB的
;EF是AC的
。
(3)AB、AC的中垂线的交点O到A、B、C的距离
。
N
M
F
E
O
A
B
C
相等
垂直平分线
垂直平分线
相等
探
索
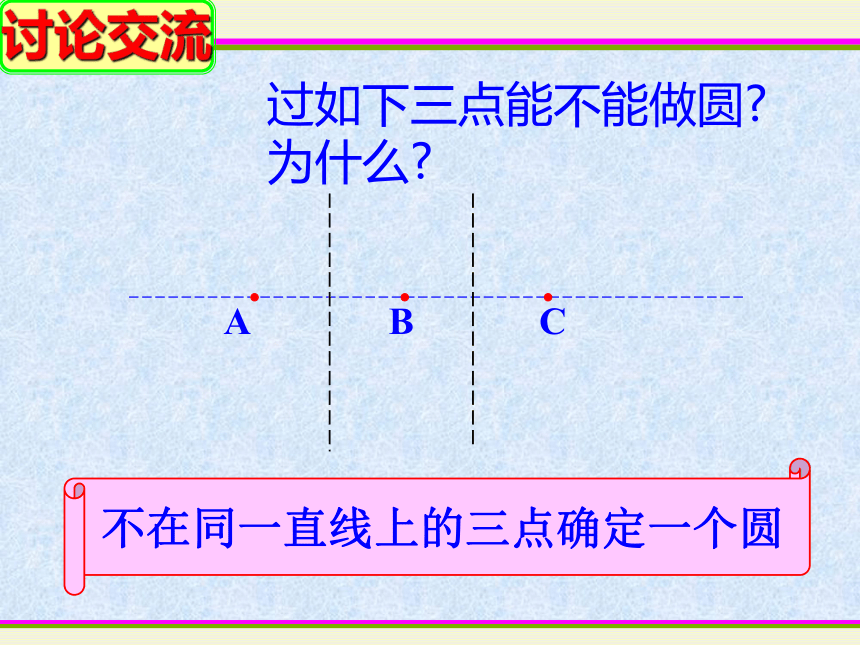
A
B
C
过如下三点能不能做圆
为什么
不在同一直线上的三点确定一个圆
讨论交流
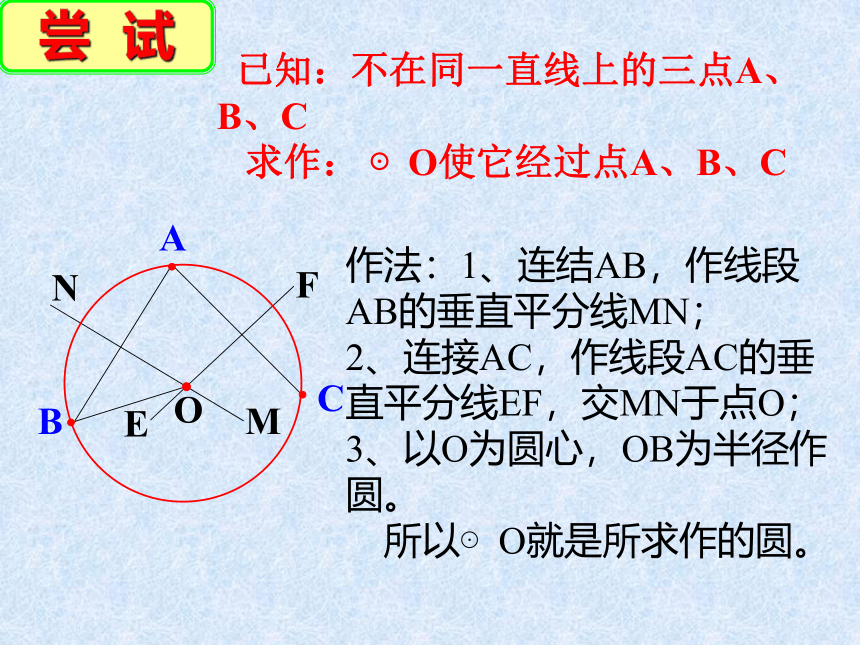
已知:不在同一直线上的三点A、B、C
求作:
⊙O使它经过点A、B、C
作法:1、连结AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆。
所以⊙O就是所求作的圆。
O
N
M
F
E
A
B
C
尝
试
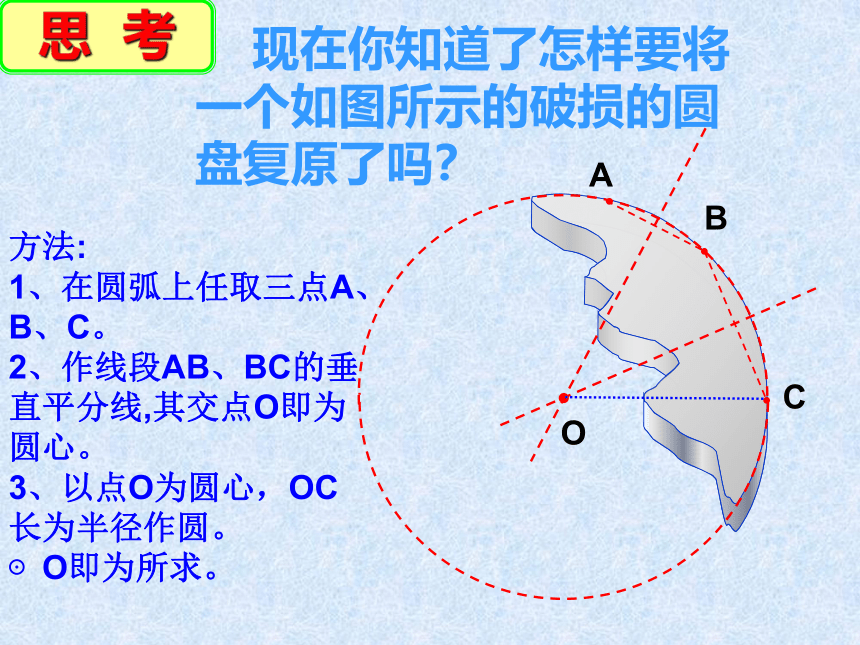
现在你知道了怎样要将一个如图所示的破损的圆盘复原了吗?
方法:
1、在圆弧上任取三点A、B、C。
2、作线段AB、BC的垂直平分线,其交点O即为圆心。
3、以点O为圆心,OC长为半径作圆。
⊙O即为所求。
A
B
C
O
思
考
已知△ABC,用直尺和圆规作出过点A、B、C的圆
A
B
C
O
练
习
经过三角形各个顶点的圆
叫做三角形的外接圆,外接圆
的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形。
如图:⊙O是△ABC的外接圆,
△ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等。
C
A
B
O
定
义
如图,请找出图中圆的圆心,并写出你找圆心的方法
A
B
C
O
探
索
画出过以下三角形的顶点的圆
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
1、比较这三个三角形外心的位置,你有何发现?
(图一)
(图二)
(图三)
2、图二中,若AB=3,BC=4,则它的外接圆半径是多少?
练
习
图中工具的CD边所在直线恰好垂直平分AB边,怎样用这个工具找出一个圆的圆心。
C
A
B
D
·圆心
画一画
1、判断:
(1)经过三点一定可以作圆。(
)
(2)三角形的外心就是这个三角形两边垂直平分线的交点。(
)
(3)三角形的外心到三边的距离相等。(
)
(4)等腰三角形的外心一定在这个三角形内。(
)
练
习
2、下列命题不正确的是
A.过一点有无数个圆.
B.过两点有无数个圆.
C.弦是圆的一部分.
D.过同一直线上三点不能画圆.
3、三角形的外心具有的性质是
A.到三边的距离相等.
B.到三个顶点的距离相等.
C.外心在三角形的外.
D.外心在三角形内.
练
习
(1)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定。
(2)经过一个已知点能作无数个圆!
(3)经过两个已知点A、B能作无数个圆!这些圆的圆心在线段AB的垂直平分线上。
(4)不在同一直线上的三个点确定一个圆。
(5)外接圆,外心的概念。
注
意
延伸拓展
1、求边长为8的等边三角形的外接圆半径
延伸拓展
2、已知△ABC中,AB=AC=10,BC=12,求△ABC的外接圆半径
3、如图,一根5m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域.
5
5m
o
4m
5m
o
4m
正确答案
大家快算算!
通过本课的学习,你又有
什么收获?
回顾总结
初中数学九年级上册
(苏科版)
2.3
确定圆的条件
1、过一点可以作几条直线?
2、过几点可确定一条直线?
过几点可以确定一个圆呢?
回
顾
一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
要确定一个圆必须确定几个条件
情景创设
经过一个已知点A能确定一个圆吗
A
经过一个已知点能作无数个圆
你怎样画这个圆
探
索
经过两个已知点A、B能确定一个圆吗
A
B
经过两个已知点A、B能作无数个圆
经过两个已知点A、B所作的圆的圆心在怎样的一条直线上
它们的圆心都在线段AB的中垂线上。
探
索
经过三个已知点A,B,C能确定一个圆吗?
假设经过A、B、C三点的⊙O存在
(1)圆心O到A、B、C三点距离
(填“相等”或”不相等”)。
(2)连结AB、AC,过O点
分别作直线MN⊥AB,
EF⊥AC,则MN是AB的
;EF是AC的
。
(3)AB、AC的中垂线的交点O到A、B、C的距离
。
N
M
F
E
O
A
B
C
相等
垂直平分线
垂直平分线
相等
探
索
A
B
C
过如下三点能不能做圆
为什么
不在同一直线上的三点确定一个圆
讨论交流
已知:不在同一直线上的三点A、B、C
求作:
⊙O使它经过点A、B、C
作法:1、连结AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆。
所以⊙O就是所求作的圆。
O
N
M
F
E
A
B
C
尝
试
现在你知道了怎样要将一个如图所示的破损的圆盘复原了吗?
方法:
1、在圆弧上任取三点A、B、C。
2、作线段AB、BC的垂直平分线,其交点O即为圆心。
3、以点O为圆心,OC长为半径作圆。
⊙O即为所求。
A
B
C
O
思
考
已知△ABC,用直尺和圆规作出过点A、B、C的圆
A
B
C
O
练
习
经过三角形各个顶点的圆
叫做三角形的外接圆,外接圆
的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形。
如图:⊙O是△ABC的外接圆,
△ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等。
C
A
B
O
定
义
如图,请找出图中圆的圆心,并写出你找圆心的方法
A
B
C
O
探
索
画出过以下三角形的顶点的圆
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
1、比较这三个三角形外心的位置,你有何发现?
(图一)
(图二)
(图三)
2、图二中,若AB=3,BC=4,则它的外接圆半径是多少?
练
习
图中工具的CD边所在直线恰好垂直平分AB边,怎样用这个工具找出一个圆的圆心。
C
A
B
D
·圆心
画一画
1、判断:
(1)经过三点一定可以作圆。(
)
(2)三角形的外心就是这个三角形两边垂直平分线的交点。(
)
(3)三角形的外心到三边的距离相等。(
)
(4)等腰三角形的外心一定在这个三角形内。(
)
练
习
2、下列命题不正确的是
A.过一点有无数个圆.
B.过两点有无数个圆.
C.弦是圆的一部分.
D.过同一直线上三点不能画圆.
3、三角形的外心具有的性质是
A.到三边的距离相等.
B.到三个顶点的距离相等.
C.外心在三角形的外.
D.外心在三角形内.
练
习
(1)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定。
(2)经过一个已知点能作无数个圆!
(3)经过两个已知点A、B能作无数个圆!这些圆的圆心在线段AB的垂直平分线上。
(4)不在同一直线上的三个点确定一个圆。
(5)外接圆,外心的概念。
注
意
延伸拓展
1、求边长为8的等边三角形的外接圆半径
延伸拓展
2、已知△ABC中,AB=AC=10,BC=12,求△ABC的外接圆半径
3、如图,一根5m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域.
5
5m
o
4m
5m
o
4m
正确答案
大家快算算!
通过本课的学习,你又有
什么收获?
回顾总结
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
