苏科版九年级数学上册 4.3 等可能条件下的概率(二)课件(15张)
文档属性
| 名称 | 苏科版九年级数学上册 4.3 等可能条件下的概率(二)课件(15张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 954.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 10:16:31 | ||
图片预览






文档简介
(共15张PPT)
4.3等可能条件下的概率(二)
如图是配紫色游戏中的两个转盘,你能用列表的方法求出配成紫色的概率是多少?
A盘
B盘
回顾旧知:
出示一个带指针的转盘,任意转动这个转盘,如果在某个时刻观察指针的位置
.
问题1:这时所有可能结果有多少个?
问题2:每次观察有几个结果?
问题3:每个结果出现的机会是均等的吗?
情境1:
自学提示1:
问题1:在转动的过程中当正好转了一周时指针指向每一个扇形区域机会均等吗?那么指针指向每一个扇形区域是等可能性吗?
1
2
3
4
5
6
7
8
情境2:
自学提示2:
问题2:怎样求指针指向每一个扇形区域的概率?它们的概率分别是多少?
问题1:每个转盘转到红色与蓝色的可能性相同吗?
情境3:
问题2:第一个转盘转一周时,试验结果有几个,其中有几个结果指向红色区域?概率是多少?
问题3:用同样的方法研究第二个转盘,则第二个转盘指向红色区域的概率是多少?
抢答环节
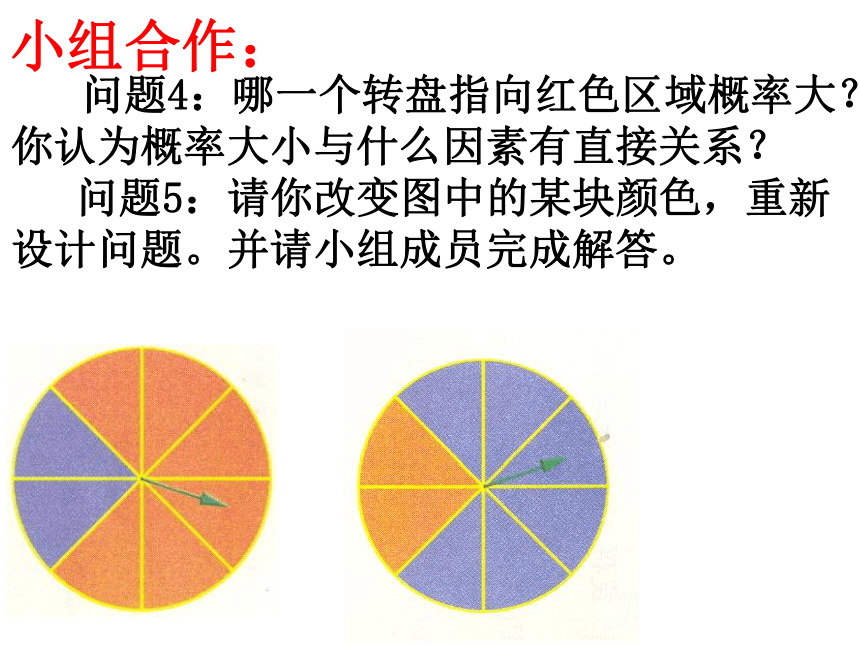
问题4:哪一个转盘指向红色区域概率大?你认为概率大小与什么因素有直接关系?
问题5:请你改变图中的某块颜色,重新设计问题。并请小组成员完成解答。
小组合作:
例1:某商场为了吸引顾客,开展有奖销售活动,设立了一个可以自由转动的转盘,转盘等分为16份,其中红色1份、蓝色2份、黄色4份、白色9份,商场规定:顾客每购满1000元的商品,就可获得一次转动转盘的机会,转盘停止时,指针指向红、蓝、黄区域,顾客可分别获得1000元、200元、100元的礼品,某顾客购物1400元,他获得礼品的概率是多少?他分别获得1000元、200元、100元礼品的概率是多少?
1、说出这位顾客有无获得一次转动转盘的机会?为什么?
2、这个问题在试验过程中共有多少个结果?获得礼品的结果有几次?怎样求获得1000元礼品的概率?
3、用同样的方法可求其余的概率。
小组讨论:
例2:在4m
远外向地毯扔沙包,地毯中每一块小正方形除颜色外完全相同,假定沙包击中每一块小正方形是等可能的,扔沙包1次,击中红色区域的概率多大?
问题1:这个问题可转化为等
可能条件下的概率(一)吗?
问题2:在试验过程中,这些正
方形除颜色外都相同,每扔一
次沙包一次击中每一块小正方
形的可能性都相同吗?
问题3:在试验过程中每扔一次
沙包所有可能发生的结果有多
少个?击中红色区域的可能性结
果有几个?概率是多少?
小组展示:
设计一转盘或方格,使指针或飞标指向红色区域的概率为
指针指向黄色区域的概率为
,指针指向蓝色区域概率为
.
小小设计师:
宝应白田路和泰山路交叉路口,目前由东向西红绿灯时间设置是:红灯32s,绿灯35s,黄灯3s.桑老师匀速骑车由西向东通过路口,可以直接通过的概率是多大?
实际运用:
问题1:等可能条件下的概率这节课的特点是什么?
问题2:如何求等可能条件下的概率(二)事件的概率
小结:
如图,一只苍蝇在画有图案的纸上任意爬行,它刚好爬行在阴影部分上的概率是多少?
勇攀高峰:
某校九年级1、2班联合举行晚会。组织者为了使晚会气氛活跃,策划时计划整台晚会以转盘游戏的方式进行:每个节目开始时,两班各派一人先进行转盘游戏,胜者获得一件奖品,负者表演一个节目.1班的文娱委员利用分别标有数字1、2、3和4、5、6、7的两个转盘(如图)设计了一种游戏方案:两人同时各转动一个转盘一次,将得到的数字相乘,积为偶数时,1班代表胜,否则2班代表胜.你认为该方案对双方是否公平?为什么?
勇攀高峰:
4.3等可能条件下的概率(二)
如图是配紫色游戏中的两个转盘,你能用列表的方法求出配成紫色的概率是多少?
A盘
B盘
回顾旧知:
出示一个带指针的转盘,任意转动这个转盘,如果在某个时刻观察指针的位置
.
问题1:这时所有可能结果有多少个?
问题2:每次观察有几个结果?
问题3:每个结果出现的机会是均等的吗?
情境1:
自学提示1:
问题1:在转动的过程中当正好转了一周时指针指向每一个扇形区域机会均等吗?那么指针指向每一个扇形区域是等可能性吗?
1
2
3
4
5
6
7
8
情境2:
自学提示2:
问题2:怎样求指针指向每一个扇形区域的概率?它们的概率分别是多少?
问题1:每个转盘转到红色与蓝色的可能性相同吗?
情境3:
问题2:第一个转盘转一周时,试验结果有几个,其中有几个结果指向红色区域?概率是多少?
问题3:用同样的方法研究第二个转盘,则第二个转盘指向红色区域的概率是多少?
抢答环节
问题4:哪一个转盘指向红色区域概率大?你认为概率大小与什么因素有直接关系?
问题5:请你改变图中的某块颜色,重新设计问题。并请小组成员完成解答。
小组合作:
例1:某商场为了吸引顾客,开展有奖销售活动,设立了一个可以自由转动的转盘,转盘等分为16份,其中红色1份、蓝色2份、黄色4份、白色9份,商场规定:顾客每购满1000元的商品,就可获得一次转动转盘的机会,转盘停止时,指针指向红、蓝、黄区域,顾客可分别获得1000元、200元、100元的礼品,某顾客购物1400元,他获得礼品的概率是多少?他分别获得1000元、200元、100元礼品的概率是多少?
1、说出这位顾客有无获得一次转动转盘的机会?为什么?
2、这个问题在试验过程中共有多少个结果?获得礼品的结果有几次?怎样求获得1000元礼品的概率?
3、用同样的方法可求其余的概率。
小组讨论:
例2:在4m
远外向地毯扔沙包,地毯中每一块小正方形除颜色外完全相同,假定沙包击中每一块小正方形是等可能的,扔沙包1次,击中红色区域的概率多大?
问题1:这个问题可转化为等
可能条件下的概率(一)吗?
问题2:在试验过程中,这些正
方形除颜色外都相同,每扔一
次沙包一次击中每一块小正方
形的可能性都相同吗?
问题3:在试验过程中每扔一次
沙包所有可能发生的结果有多
少个?击中红色区域的可能性结
果有几个?概率是多少?
小组展示:
设计一转盘或方格,使指针或飞标指向红色区域的概率为
指针指向黄色区域的概率为
,指针指向蓝色区域概率为
.
小小设计师:
宝应白田路和泰山路交叉路口,目前由东向西红绿灯时间设置是:红灯32s,绿灯35s,黄灯3s.桑老师匀速骑车由西向东通过路口,可以直接通过的概率是多大?
实际运用:
问题1:等可能条件下的概率这节课的特点是什么?
问题2:如何求等可能条件下的概率(二)事件的概率
小结:
如图,一只苍蝇在画有图案的纸上任意爬行,它刚好爬行在阴影部分上的概率是多少?
勇攀高峰:
某校九年级1、2班联合举行晚会。组织者为了使晚会气氛活跃,策划时计划整台晚会以转盘游戏的方式进行:每个节目开始时,两班各派一人先进行转盘游戏,胜者获得一件奖品,负者表演一个节目.1班的文娱委员利用分别标有数字1、2、3和4、5、6、7的两个转盘(如图)设计了一种游戏方案:两人同时各转动一个转盘一次,将得到的数字相乘,积为偶数时,1班代表胜,否则2班代表胜.你认为该方案对双方是否公平?为什么?
勇攀高峰:
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
