苏科版九年级数学上册 3.4 方差课件(17张)
文档属性
| 名称 | 苏科版九年级数学上册 3.4 方差课件(17张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
3.4 方差
九年级(上册)
初中数学
3.4
方差
生活数学
A厂:40.0,39.9,40.0,40.1,40.2,
39.8,40.0,39.9,40.0,40.1;
你能从哪些角度认识这些数据?
乒乓球的标准直径为40mm.质检部门对A、B两厂生产
的乒乓球的直径进行检测,从A、B两厂生产的乒乓球中各
抽取了部分乒乓球,其中A厂测量结果如下(单位:mm):
B厂:40.0,40.1,39.8,40.1,
39.9,40.2,39.9,40.0.
3.4
方差
数据分析
集中趋势:平均数、中位数、众数;
反映的是一组数据向其中心值聚集的程度。
离散程度:
、
;
反映的是一组数据偏离其中心值的程度。
极差
方差
3.4
方差
问题
A厂:40.0,39.9,40.0,40.1,40.2,
39.8,40.0,39.9,40.0,40.1;
极差=最大值-最小值.
怎样更精确地比较这两组数据的离散程度呢?
极差在一定程度上描述了一组数据的离散(波动)程度.
B厂:40.0,40.1,39.8,40.1,
39.9,40.2,39.9,40.0.
3.4
方差
40.3
40.2
39.7
40.1
40.0
39.9
39.8
40.3
40.2
39.7
40.1
40.0
39.9
39.8
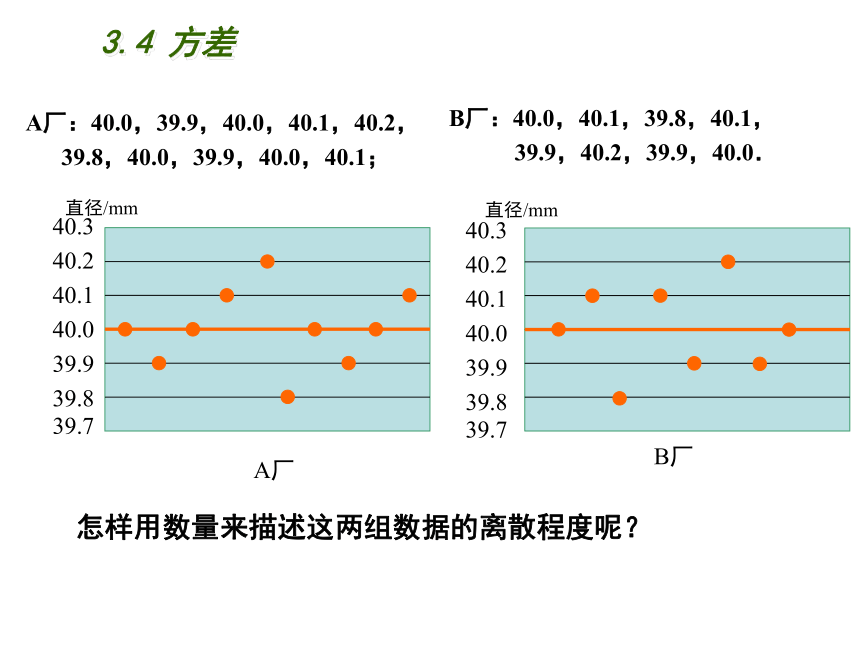
A厂
B厂
直径/mm
直径/mm
怎样用数量来描述这两组数据的离散程度呢?
A厂:40.0,39.9,40.0,40.1,40.2,
39.8,40.0,39.9,40.0,40.1;
B厂:40.0,40.1,39.8,40.1,
39.9,40.2,39.9,40.0.
3.4
方差
x1
x2
x3
x4
x5
x6
x7
x8
x9
x10
数据
40.0
39.9
40.0
40.1
40.2
39.8
40.0
39.9
40.0
40.1
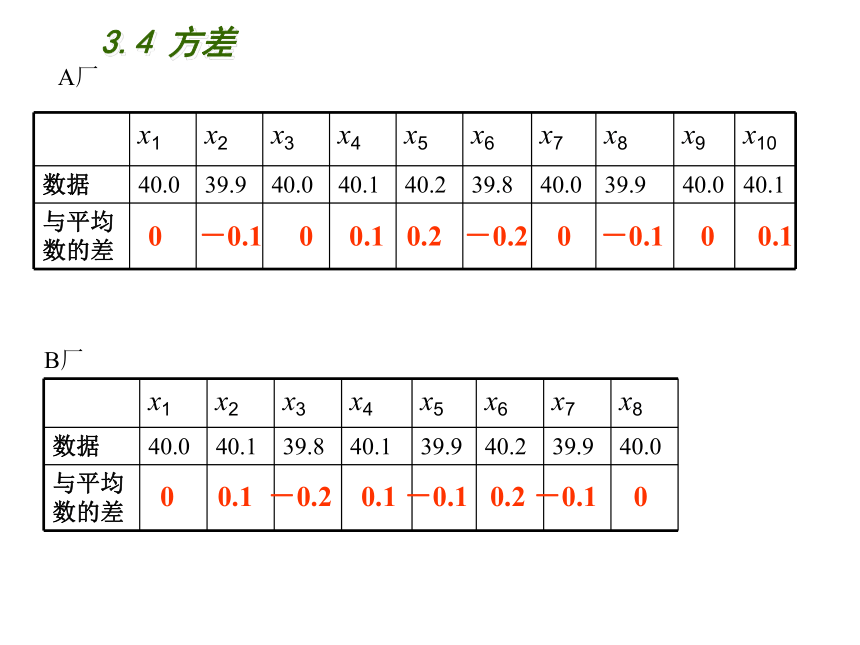
与平均数的差
x1
x2
x3
x4
x5
x6
x7
x8
数据
40.0
40.1
39.8
40.1
39.9
40.2
39.9
40.0
与平均数的差
A厂
0
-0.1
0
0.1
0.2
-0.2
0
-0.1
0
0.1
0
0.1
-0.2
0.1
-0.1
0.2
-0.1
0
B厂
3.4
方差
x1
x2
x3
x4
x5
x6
x7
x8
x9
x10
数据
40.0
39.9
40.0
40.1
40.2
39.8
40.0
39.9
40.0
40.1
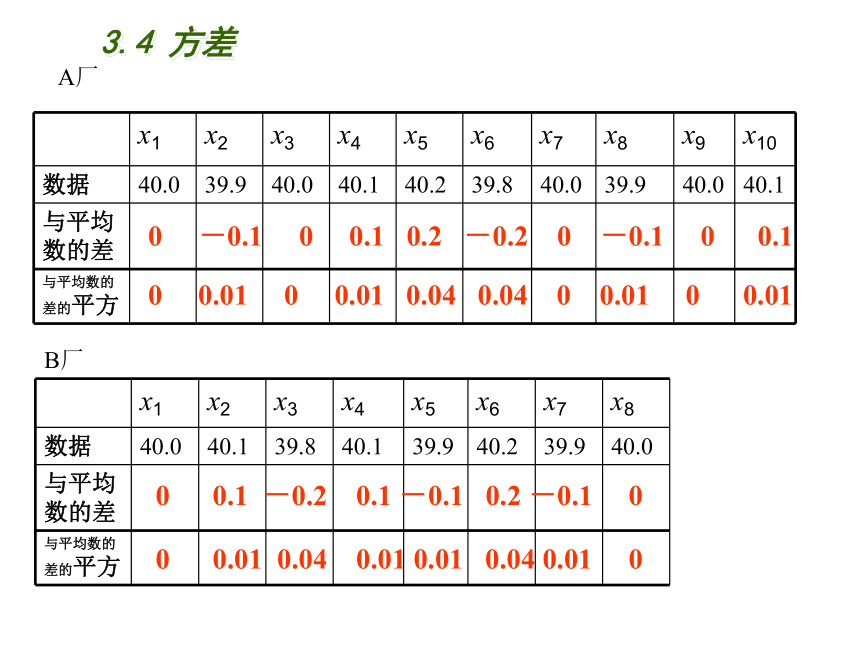
与平均数的差
与平均数的差的平方
x1
x2
x3
x4
x5
x6
x7
x8
数据
40.0
40.1
39.8
40.1
39.9
40.2
39.9
40.0
与平均数的差
与平均数的差的平方
A厂
0
-0.1
0
0.1
0.2
-0.2
0
-0.1
0
0.1
0
0.1
-0.2
0.1
-0.1
0.2
-0.1
0
B厂
0
0.01
0
0.01
0.04
0.04
0
0.01
0
0.01
0
0.01
0.04
0.01
0.01
0.04
0.01
0
★我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况。这个结果通常称为方差.
通常用S2表示一组数据的方差,用
x
表示一组数据的平均数,x1、x2、…..表示各个数据。
A厂:40.0,39.9,40.0,40.1,40.2,
39.8,40.0,39.9,40.0,40.1;
B厂:40.0,40.1,39.8,40.1,
39.9,40.2,39.9,40.0.
由
,可知A厂生产的乒乓球直径的离散程度较小,说明A厂生产的乒乓球质量比较稳定.
3.4
方差
例题
在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了
舞剧《天鹅湖》,参加表演的女演员身高(单位:cm)如
下表所示:
甲
163
164
164
165
165
166
166
167
乙
163
165
165
166
166
167
168
168
哪个芭蕾舞团女演员的身高更整齐?
3.4
方差
一、知识小结
(1)求极差:极差=最大值-最小值
(2)求方差:先平均,再求差,然后平方,
最后再平均
.
对于一组数据,有时只知道它的平均数还不够,还需要知道它的离散程度;而描述一组数据的离散程度的量最常用的是极差和方差.
二、方法小结
3.甲、乙两名战士在射击训练中,打靶的次数相同,且射击成绩的平均数x甲
=
x乙,如果甲的射击成绩比较稳定,那么方差的大小关系是S2甲————S2乙。
<
2.一个样本的方差是
则这个样本中的数据个数是____,平均数是____
100
8
19℃
1.某地某日最高气温为12℃,最低气温为-7
℃,该地日气温的极差是
.
3.4
方差
4.在某旅游景区上山的一条小路上,有一些断断续续的台阶.下图是其中的甲、乙段台阶路的示意图(图中的数字表示每一级台阶的高度).请你回答下列问题(单位:cm):
乙路段
16
14
14
16
15
甲路段
15
11
15
18
17
10
19
(1)哪段台阶路走起来更舒服?
为什么?
(2)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
已知四组数据1、2、3、4、5;11、12、13、14、15;
3、6、9、12、15和4、7、10、13、16。
1、填表
2、对照以上结果,你能从中发现哪些有趣的联系?
数据
平均数
方差
1、2、3、4、5
11、12、13、14、15
3、6、9、12、15
4、7、10、13、16
3
2
13
2
9
18
10
18
已知一组数据x1,x2,…,xn的方差是a。
(1)数据x1-4、x2-4,…,xn-4的方差是
;
(2)数据
3x1,3x2,…,3xn的方差是
。
(3)数据3x1-4,3x2-4,…,3xn-4
的方差是_
_。
9a
9a
a
3.4
方差
1.课本P115
读一读:标准差;
2.课本P125
探索研究:13题:平均差。
3.4
方差
3.4 方差
九年级(上册)
初中数学
3.4
方差
生活数学
A厂:40.0,39.9,40.0,40.1,40.2,
39.8,40.0,39.9,40.0,40.1;
你能从哪些角度认识这些数据?
乒乓球的标准直径为40mm.质检部门对A、B两厂生产
的乒乓球的直径进行检测,从A、B两厂生产的乒乓球中各
抽取了部分乒乓球,其中A厂测量结果如下(单位:mm):
B厂:40.0,40.1,39.8,40.1,
39.9,40.2,39.9,40.0.
3.4
方差
数据分析
集中趋势:平均数、中位数、众数;
反映的是一组数据向其中心值聚集的程度。
离散程度:
、
;
反映的是一组数据偏离其中心值的程度。
极差
方差
3.4
方差
问题
A厂:40.0,39.9,40.0,40.1,40.2,
39.8,40.0,39.9,40.0,40.1;
极差=最大值-最小值.
怎样更精确地比较这两组数据的离散程度呢?
极差在一定程度上描述了一组数据的离散(波动)程度.
B厂:40.0,40.1,39.8,40.1,
39.9,40.2,39.9,40.0.
3.4
方差
40.3
40.2
39.7
40.1
40.0
39.9
39.8
40.3
40.2
39.7
40.1
40.0
39.9
39.8
A厂
B厂
直径/mm
直径/mm
怎样用数量来描述这两组数据的离散程度呢?
A厂:40.0,39.9,40.0,40.1,40.2,
39.8,40.0,39.9,40.0,40.1;
B厂:40.0,40.1,39.8,40.1,
39.9,40.2,39.9,40.0.
3.4
方差
x1
x2
x3
x4
x5
x6
x7
x8
x9
x10
数据
40.0
39.9
40.0
40.1
40.2
39.8
40.0
39.9
40.0
40.1
与平均数的差
x1
x2
x3
x4
x5
x6
x7
x8
数据
40.0
40.1
39.8
40.1
39.9
40.2
39.9
40.0
与平均数的差
A厂
0
-0.1
0
0.1
0.2
-0.2
0
-0.1
0
0.1
0
0.1
-0.2
0.1
-0.1
0.2
-0.1
0
B厂
3.4
方差
x1
x2
x3
x4
x5
x6
x7
x8
x9
x10
数据
40.0
39.9
40.0
40.1
40.2
39.8
40.0
39.9
40.0
40.1
与平均数的差
与平均数的差的平方
x1
x2
x3
x4
x5
x6
x7
x8
数据
40.0
40.1
39.8
40.1
39.9
40.2
39.9
40.0
与平均数的差
与平均数的差的平方
A厂
0
-0.1
0
0.1
0.2
-0.2
0
-0.1
0
0.1
0
0.1
-0.2
0.1
-0.1
0.2
-0.1
0
B厂
0
0.01
0
0.01
0.04
0.04
0
0.01
0
0.01
0
0.01
0.04
0.01
0.01
0.04
0.01
0
★我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况。这个结果通常称为方差.
通常用S2表示一组数据的方差,用
x
表示一组数据的平均数,x1、x2、…..表示各个数据。
A厂:40.0,39.9,40.0,40.1,40.2,
39.8,40.0,39.9,40.0,40.1;
B厂:40.0,40.1,39.8,40.1,
39.9,40.2,39.9,40.0.
由
,可知A厂生产的乒乓球直径的离散程度较小,说明A厂生产的乒乓球质量比较稳定.
3.4
方差
例题
在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了
舞剧《天鹅湖》,参加表演的女演员身高(单位:cm)如
下表所示:
甲
163
164
164
165
165
166
166
167
乙
163
165
165
166
166
167
168
168
哪个芭蕾舞团女演员的身高更整齐?
3.4
方差
一、知识小结
(1)求极差:极差=最大值-最小值
(2)求方差:先平均,再求差,然后平方,
最后再平均
.
对于一组数据,有时只知道它的平均数还不够,还需要知道它的离散程度;而描述一组数据的离散程度的量最常用的是极差和方差.
二、方法小结
3.甲、乙两名战士在射击训练中,打靶的次数相同,且射击成绩的平均数x甲
=
x乙,如果甲的射击成绩比较稳定,那么方差的大小关系是S2甲————S2乙。
<
2.一个样本的方差是
则这个样本中的数据个数是____,平均数是____
100
8
19℃
1.某地某日最高气温为12℃,最低气温为-7
℃,该地日气温的极差是
.
3.4
方差
4.在某旅游景区上山的一条小路上,有一些断断续续的台阶.下图是其中的甲、乙段台阶路的示意图(图中的数字表示每一级台阶的高度).请你回答下列问题(单位:cm):
乙路段
16
14
14
16
15
甲路段
15
11
15
18
17
10
19
(1)哪段台阶路走起来更舒服?
为什么?
(2)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
已知四组数据1、2、3、4、5;11、12、13、14、15;
3、6、9、12、15和4、7、10、13、16。
1、填表
2、对照以上结果,你能从中发现哪些有趣的联系?
数据
平均数
方差
1、2、3、4、5
11、12、13、14、15
3、6、9、12、15
4、7、10、13、16
3
2
13
2
9
18
10
18
已知一组数据x1,x2,…,xn的方差是a。
(1)数据x1-4、x2-4,…,xn-4的方差是
;
(2)数据
3x1,3x2,…,3xn的方差是
。
(3)数据3x1-4,3x2-4,…,3xn-4
的方差是_
_。
9a
9a
a
3.4
方差
1.课本P115
读一读:标准差;
2.课本P125
探索研究:13题:平均差。
3.4
方差
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
