2.1.1 认识一元二次方程(1) 课件(共28张PPT)
文档属性
| 名称 | 2.1.1 认识一元二次方程(1) 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 20:29:05 | ||
图片预览






文档简介
(共28张PPT)
2.1.1
认识一元二次方程(1)
第二章
一元二次方程
2021-2022学年九年级数学上册同步(北师版)
学习目标
1.理解一元二次方程的概念.
2.根据一元二次方程的一般形式,确定各项系数.
3.理解并灵活运用一元二次方程概念解决有关问题.
导入新课
没有未知数
回顾:下列式子是方程吗?
(1)
3+6=9
(2)
5x+3
(3)
3x-5<18
代数式
不等式
什么叫方程?
含有未知数的等式叫做方程.
(4)
x+5
=3
方程
导入新课
回顾:下列的式子是什么方程?
(1)
5x-6=12
(2)
2x+3y=9
一元一次方程
二元一次方程
分式方程
一元一次方程
二元一次方程
分式方程
学过的方程
整式方程
一元二次方程的概念
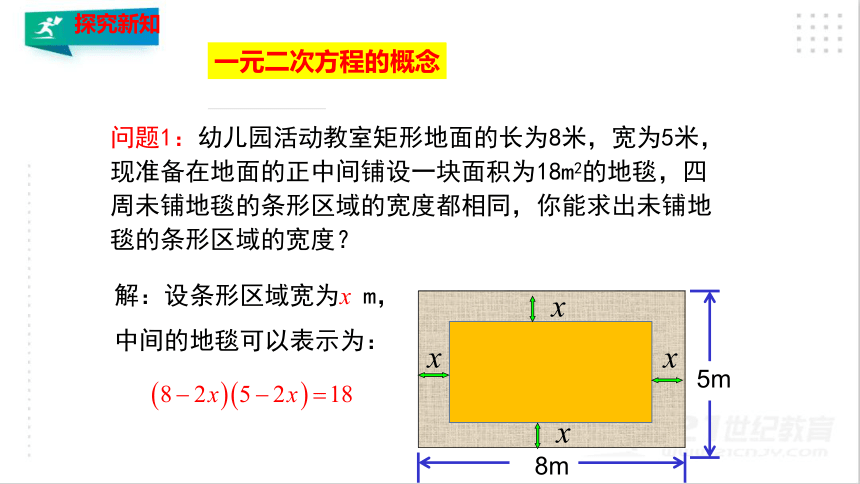
问题1:幼儿园活动教室矩形地面的长为8米,宽为5米,现准备在地面的正中间铺设一块面积为18m2的地毯,四周未铺地毯的条形区域的宽度都相同,你能求出未铺地毯的条形区域的宽度?
5m
8m
解:设条形区域宽为x
m,
中间的地毯可以表示为:
探究新知
问题2:观察下面等式:102
+
112
+
122
=
132
+
142
你还能找到其他的五个连续整数,使前三个数的平方和等于后两个数的平方和吗?
解:如果设五个连续整数中的第一个数为x,那么后面四个数依次可表示为
x+1,
x+2,
x+3,
x+4
x2
+
(x
+
1)2
+
(x
+
2)2
=
(x
+
3)2
+
(x
+
4)2
探究新知
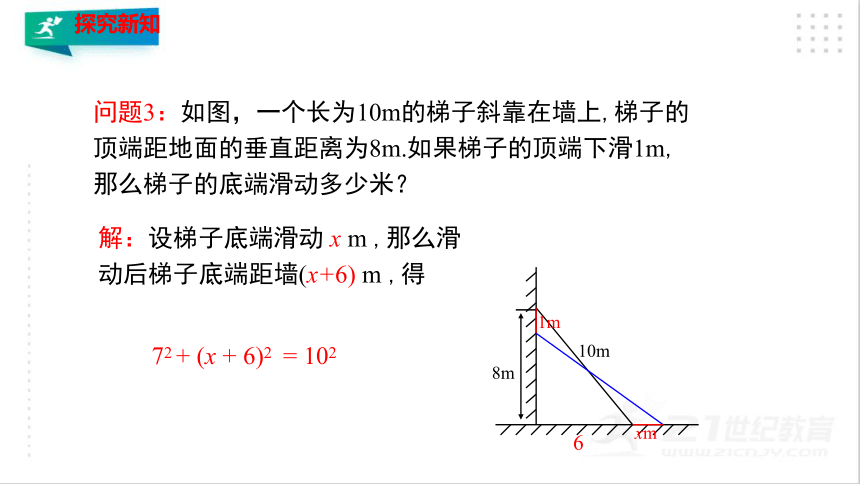
解:设梯子底端滑动
x
m
,那么滑动后梯子底端距墙(x+6)
m
,得
问题3:如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?
6
72
+
(x
+
6)2
=
102
10m
8m
1m
xm
探究新知
化简成:
①
2x2
-
13x
+
11
=
0
;
②
x2
-
8x
-
20=0;
③
x2
+
12
x
-
15
=
0.
上面的问题,我们得到三个方程
x2
+
(x
+
1)2
+
(x
+
2)2
=
(x
+
3)2
+
(x
+
4)2.
72
+
(x
+
6)2
=
102
(8-2x)
(5-2x
)
=18
观察它们有什么共同特点?
探究新知
①
2x2
-
13x
+
11
=
0
;
②
x2
-
8x
-
20=0;
③
x2
+
12
x
-
15
=
0.
1.只含有一个未知数;
2.未知数的最高次数是2;
3.整式方程.
观察它们有什么共同特点?
特点:
只含有一个未知数x的整式方程,并且都可以化为ax2+bx+c=0(a,b,c为常数,
a≠0)的形式,这样的方程叫做一元二次方程.
探究新知
ax2+bx
+c
=
0(a
,b
,c为常数,
a≠0)
ax2
称为二次项,
a
称为二次项系数.
bx
称为一次项,
b
称为一次项系数.
c
称为常数项.
一元二次方程的一般形式:
例:
2x2
-
13x
+
11
=0
二次项为
2x2;一次项为-
13x;常数项为11;
二次项系数为2;一次项系数为-13
★注意:系数和项均包含前面的符号.
探究新知
思考:一般式ax2+bx+c=0要求a≠0,b、c
可以为零吗?
当
a
=
0
时
bx+c
=
0
当a
≠
0,b
=
0时
,
ax2+c
=
0
当a
≠
0,c
=
0时
,
ax2+bx
=
0
当a
≠
0,b
=c=0时
ax2
=
0
总结:一元二次方程要满足a
≠
0
,b,c
可为任意实数.
一元一次方程
一元二次方程
探究新知
判断下列方程中,哪些是一元二次方程
(1)
x2
+
–
3=0
(2)x3
–
x+4=0
(3)
x2
–
2xy
–
3=0
(4)
ay2
+by
+c=0
(5)
2x2=0
(6)2x2+3x
–
2=2x2-1
(
X
)
(
X
)
(
X
)
(
X
)
(
√
)
(
X
)
不是整式方程
未知数最高次为3次
两个未知数
化简为3x-1=0,是一元一次方程
不是一般式先进一步化简整理后再作判断.
要求a≠0
练一练
1.只含有一个未知数;
2.未知数的最高次数是2;
3.整式方程.
注意:(1)若二次项的系数是参数,要保证二次项的系数不为0;
(2)当给出的不是一般式,先进一步化简整理后再作判断
一元二次方程的条件:
归纳总结
典例精析
例1
下列选项中,关于x的一元二次方程的是(
)
C
不是整式方程
含两个未知数
化简整理成
x2-3x+2=0
少了限制条件
a≠0
提示
判断一个方程是不是一元二次方程,首先看是不是整式方程;如是再进一步化简整理后再作判断.
例2:a为何值时,下列方程为一元二次方程?
(1)ax2-x=2x2
(2)(a-1)x
∣
a
∣
+1
-2x-7=0
解:(1)将方程式转化为一般形式,得(a-2)x2-x=0,所以当a-2≠0,即a≠2时,原方程是一元二次方程;
(2)由∣a
∣+1
=2,且a-1
≠0知,当a=-1时,原方程是一元二次方程.
方法总结:用一元二次方程的定义求字母的值的方法:根据未知数的最高次数等于2,列出关于某个字母的方程,再排除使二次项系数等于0的字母的值.
典例精析
例3
将方程3x(x-1)=5(x+2)化为一般形式,并分别指出它们的二次项、一次项和常数项及它们的系数.
解:
去括号,得
3x2-3x=5x+10.
移项、合并同类项,得一元二次方程的一般形式
3x2-8x-10=0.
其中二次项是3x2,系数是3;一次项是-8x,系数是-8;常数项是-10.
系数和项均包含前面的符号.
注意
典例精析
1.
在下列方程中,一元二次方程是(
)
x2-2xy+y2=0
x(x+3)=x2-1
x2-2x=3
x
+
=0
C
课堂练习
2.若方程(m-3)xn+2x-3=0是关于x的一元二次方程,则(
)
A.
m=3,n≠2
B.
m=3,n=2
C.
m≠3,n=2
D.
m≠3,n≠2
C
3.
方程x2-2x-4=0的二次项系数和一次项系数分别为(
)
1和2
B.
1和-2
C.
1和-4
D.
1和4
C
课堂练习
4.下列选项中,关于x的一元二次方程的是(
)
C
5.把方程-2x2+x+8=1化为二次项系数为正数的一般形式时,它的常数项是(
)
A.7
B.-7
C.-8
D.-9
B
课堂练习
6.方程2x2-6x-5=0的二次项系数,一次项系数,常数项分别为
(
)
A.
6,2,5
B.
2,-6,5
C.
2,-6,-5
D.
-2,6,5
C
7.
若一元二次方程(2m+6)x2+m2-9=0的常数项是0,则m等于(
)
A.
-3
B.
3
C.
±3
D.
9
B
课堂练习
8.关于x的方程(k2
-
1)
x2
+2
(k
-
1)
x
+
2k
+
2
=
0,
当k
时,是一元二次方程.
当k
时,是一元一次方程.
≠±1
=-1
9.把方程2x(x-3)=(x+1)(x-2)+3化成ax2+bx+c=0的形式后,a,b,c的值分别是___________.
1,-5,-1
课堂练习
10.把下列方程化为一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项:
方 程
一般形式
二次项
系数
一次项
系数
常数项
3x2=
5x
-
1
(x
+
2)
(x
-
1)=6
4
-
7x2=0
3x2
-
5x
+
1
=
0
x2
+
x
-
8
=
0
3
-5
1
1
1
-8
7x2
-
4
=
0
7
0
-4
课堂练习
11.根据题意,列方程,并化成一元二次方程的一般形式.
一个直角三角形的三条边长是三个相连的整数,求斜边的长.
解:直角边最短边长为x,则另一条直角边长为x+1,故斜边长为x+2.
由勾股定理可得
x2+(x+1)2=(x+2)2.
整理得x2-2x-3=0.
课堂练习
12.如图,某中学准备在校园里利用围墙的一段再砌三面墙,围成一个周长为50
m的矩形花园ABCD(围墙MN为25
m),现在已备足砌墙的材料,请问矩形的宽AB为多少米时,使得矩形花园的面积为300
m2.
解:设宽AB为x
m,则长BC为(50-2x)m,得
x(50-2x)=300.
化简,得x2-25x+150=0.
课堂练习
13.如图,据某市交通部门统计,前年该市汽车拥有量为75万辆,两年后增加到108万辆.求该市两年来汽车拥有量的年平均增长率x应满足的方程.
解:该市两年来汽车拥有量的年平均增长率为x
整理,得
根据题意有,
课堂练习
课堂小结
一元二次方程
只含有一个未知数x的整式方程,并且
都可以化为ax2+bx+c=0(a,b,c为常数,
a≠0)的形式.
概念
ax2+bx+c=0(a
,
b
,
c为常数,
a≠0
ax2
称为二次项,a
称为二次项系数.
bx
称为一次项,b
称为一次项系数
c
称为常数项.
一般式
https://www.21cnjy.com/help/help_extract.php
2.1.1
认识一元二次方程(1)
第二章
一元二次方程
2021-2022学年九年级数学上册同步(北师版)
学习目标
1.理解一元二次方程的概念.
2.根据一元二次方程的一般形式,确定各项系数.
3.理解并灵活运用一元二次方程概念解决有关问题.
导入新课
没有未知数
回顾:下列式子是方程吗?
(1)
3+6=9
(2)
5x+3
(3)
3x-5<18
代数式
不等式
什么叫方程?
含有未知数的等式叫做方程.
(4)
x+5
=3
方程
导入新课
回顾:下列的式子是什么方程?
(1)
5x-6=12
(2)
2x+3y=9
一元一次方程
二元一次方程
分式方程
一元一次方程
二元一次方程
分式方程
学过的方程
整式方程
一元二次方程的概念
问题1:幼儿园活动教室矩形地面的长为8米,宽为5米,现准备在地面的正中间铺设一块面积为18m2的地毯,四周未铺地毯的条形区域的宽度都相同,你能求出未铺地毯的条形区域的宽度?
5m
8m
解:设条形区域宽为x
m,
中间的地毯可以表示为:
探究新知
问题2:观察下面等式:102
+
112
+
122
=
132
+
142
你还能找到其他的五个连续整数,使前三个数的平方和等于后两个数的平方和吗?
解:如果设五个连续整数中的第一个数为x,那么后面四个数依次可表示为
x+1,
x+2,
x+3,
x+4
x2
+
(x
+
1)2
+
(x
+
2)2
=
(x
+
3)2
+
(x
+
4)2
探究新知
解:设梯子底端滑动
x
m
,那么滑动后梯子底端距墙(x+6)
m
,得
问题3:如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?
6
72
+
(x
+
6)2
=
102
10m
8m
1m
xm
探究新知
化简成:
①
2x2
-
13x
+
11
=
0
;
②
x2
-
8x
-
20=0;
③
x2
+
12
x
-
15
=
0.
上面的问题,我们得到三个方程
x2
+
(x
+
1)2
+
(x
+
2)2
=
(x
+
3)2
+
(x
+
4)2.
72
+
(x
+
6)2
=
102
(8-2x)
(5-2x
)
=18
观察它们有什么共同特点?
探究新知
①
2x2
-
13x
+
11
=
0
;
②
x2
-
8x
-
20=0;
③
x2
+
12
x
-
15
=
0.
1.只含有一个未知数;
2.未知数的最高次数是2;
3.整式方程.
观察它们有什么共同特点?
特点:
只含有一个未知数x的整式方程,并且都可以化为ax2+bx+c=0(a,b,c为常数,
a≠0)的形式,这样的方程叫做一元二次方程.
探究新知
ax2+bx
+c
=
0(a
,b
,c为常数,
a≠0)
ax2
称为二次项,
a
称为二次项系数.
bx
称为一次项,
b
称为一次项系数.
c
称为常数项.
一元二次方程的一般形式:
例:
2x2
-
13x
+
11
=0
二次项为
2x2;一次项为-
13x;常数项为11;
二次项系数为2;一次项系数为-13
★注意:系数和项均包含前面的符号.
探究新知
思考:一般式ax2+bx+c=0要求a≠0,b、c
可以为零吗?
当
a
=
0
时
bx+c
=
0
当a
≠
0,b
=
0时
,
ax2+c
=
0
当a
≠
0,c
=
0时
,
ax2+bx
=
0
当a
≠
0,b
=c=0时
ax2
=
0
总结:一元二次方程要满足a
≠
0
,b,c
可为任意实数.
一元一次方程
一元二次方程
探究新知
判断下列方程中,哪些是一元二次方程
(1)
x2
+
–
3=0
(2)x3
–
x+4=0
(3)
x2
–
2xy
–
3=0
(4)
ay2
+by
+c=0
(5)
2x2=0
(6)2x2+3x
–
2=2x2-1
(
X
)
(
X
)
(
X
)
(
X
)
(
√
)
(
X
)
不是整式方程
未知数最高次为3次
两个未知数
化简为3x-1=0,是一元一次方程
不是一般式先进一步化简整理后再作判断.
要求a≠0
练一练
1.只含有一个未知数;
2.未知数的最高次数是2;
3.整式方程.
注意:(1)若二次项的系数是参数,要保证二次项的系数不为0;
(2)当给出的不是一般式,先进一步化简整理后再作判断
一元二次方程的条件:
归纳总结
典例精析
例1
下列选项中,关于x的一元二次方程的是(
)
C
不是整式方程
含两个未知数
化简整理成
x2-3x+2=0
少了限制条件
a≠0
提示
判断一个方程是不是一元二次方程,首先看是不是整式方程;如是再进一步化简整理后再作判断.
例2:a为何值时,下列方程为一元二次方程?
(1)ax2-x=2x2
(2)(a-1)x
∣
a
∣
+1
-2x-7=0
解:(1)将方程式转化为一般形式,得(a-2)x2-x=0,所以当a-2≠0,即a≠2时,原方程是一元二次方程;
(2)由∣a
∣+1
=2,且a-1
≠0知,当a=-1时,原方程是一元二次方程.
方法总结:用一元二次方程的定义求字母的值的方法:根据未知数的最高次数等于2,列出关于某个字母的方程,再排除使二次项系数等于0的字母的值.
典例精析
例3
将方程3x(x-1)=5(x+2)化为一般形式,并分别指出它们的二次项、一次项和常数项及它们的系数.
解:
去括号,得
3x2-3x=5x+10.
移项、合并同类项,得一元二次方程的一般形式
3x2-8x-10=0.
其中二次项是3x2,系数是3;一次项是-8x,系数是-8;常数项是-10.
系数和项均包含前面的符号.
注意
典例精析
1.
在下列方程中,一元二次方程是(
)
x2-2xy+y2=0
x(x+3)=x2-1
x2-2x=3
x
+
=0
C
课堂练习
2.若方程(m-3)xn+2x-3=0是关于x的一元二次方程,则(
)
A.
m=3,n≠2
B.
m=3,n=2
C.
m≠3,n=2
D.
m≠3,n≠2
C
3.
方程x2-2x-4=0的二次项系数和一次项系数分别为(
)
1和2
B.
1和-2
C.
1和-4
D.
1和4
C
课堂练习
4.下列选项中,关于x的一元二次方程的是(
)
C
5.把方程-2x2+x+8=1化为二次项系数为正数的一般形式时,它的常数项是(
)
A.7
B.-7
C.-8
D.-9
B
课堂练习
6.方程2x2-6x-5=0的二次项系数,一次项系数,常数项分别为
(
)
A.
6,2,5
B.
2,-6,5
C.
2,-6,-5
D.
-2,6,5
C
7.
若一元二次方程(2m+6)x2+m2-9=0的常数项是0,则m等于(
)
A.
-3
B.
3
C.
±3
D.
9
B
课堂练习
8.关于x的方程(k2
-
1)
x2
+2
(k
-
1)
x
+
2k
+
2
=
0,
当k
时,是一元二次方程.
当k
时,是一元一次方程.
≠±1
=-1
9.把方程2x(x-3)=(x+1)(x-2)+3化成ax2+bx+c=0的形式后,a,b,c的值分别是___________.
1,-5,-1
课堂练习
10.把下列方程化为一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项:
方 程
一般形式
二次项
系数
一次项
系数
常数项
3x2=
5x
-
1
(x
+
2)
(x
-
1)=6
4
-
7x2=0
3x2
-
5x
+
1
=
0
x2
+
x
-
8
=
0
3
-5
1
1
1
-8
7x2
-
4
=
0
7
0
-4
课堂练习
11.根据题意,列方程,并化成一元二次方程的一般形式.
一个直角三角形的三条边长是三个相连的整数,求斜边的长.
解:直角边最短边长为x,则另一条直角边长为x+1,故斜边长为x+2.
由勾股定理可得
x2+(x+1)2=(x+2)2.
整理得x2-2x-3=0.
课堂练习
12.如图,某中学准备在校园里利用围墙的一段再砌三面墙,围成一个周长为50
m的矩形花园ABCD(围墙MN为25
m),现在已备足砌墙的材料,请问矩形的宽AB为多少米时,使得矩形花园的面积为300
m2.
解:设宽AB为x
m,则长BC为(50-2x)m,得
x(50-2x)=300.
化简,得x2-25x+150=0.
课堂练习
13.如图,据某市交通部门统计,前年该市汽车拥有量为75万辆,两年后增加到108万辆.求该市两年来汽车拥有量的年平均增长率x应满足的方程.
解:该市两年来汽车拥有量的年平均增长率为x
整理,得
根据题意有,
课堂练习
课堂小结
一元二次方程
只含有一个未知数x的整式方程,并且
都可以化为ax2+bx+c=0(a,b,c为常数,
a≠0)的形式.
概念
ax2+bx+c=0(a
,
b
,
c为常数,
a≠0
ax2
称为二次项,a
称为二次项系数.
bx
称为一次项,b
称为一次项系数
c
称为常数项.
一般式
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
