2.1.2 认识一元二次方程(2) 课件(共24张PPT)
文档属性
| 名称 | 2.1.2 认识一元二次方程(2) 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1005.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 20:27:26 | ||
图片预览








文档简介
(共24张PPT)
2.1.2
认识一元二次方程(2)
第二章
一元二次方程
2021-2022学年九年级数学上册同步(北师版)
学习目标
1.会进行简单的一元二次方程的试解.
2.根据题意判定一个数是否是一元二次方程的根及利用试解方法解决一些具体问题.
3.理解方程的解的概念,培养有条理的思考与表达的能力.
导入新课
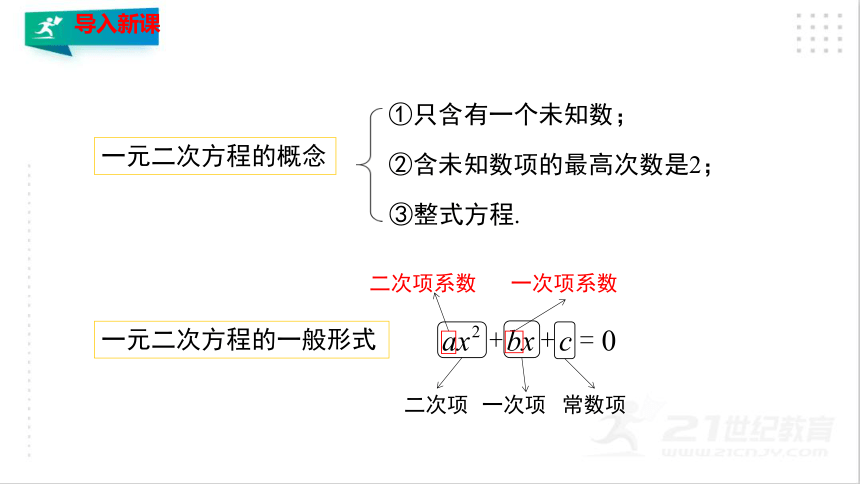
一元二次方程的概念
一元二次方程的一般形式
②含未知数项的最高次数是2;
①只含有一个未知数;
③整式方程.
二次项
一次项
常数项
二次项系数
一次项系数
一元二次方程的解
一元二次方程的根:
使一元二次方程等号两边相等的未知数的值叫作一元二次方程的解(根).
想想:下面哪些数是方程
x2
–
x
–
6
=
0
的解
-3
,
-2
,-1
,0
,1,2,3
解:当x=3时,
x2
–
x
–
6
=9-3-6=
0
当x=-2时,
x2
–
x
–
6
=4+2-6=
0
∴
x=3或x=-2都是x2
–
x
–
6
=
0的解
注意,一元二次方程可能不止一个根.
探究新知
例1:已知a是方程
x2+2x-2=0
的一个实数根,
求
2a2+4a+2018的值.
解:由题意得
方法点拨:求代数式的值,先把已知解代入,再注意观察,有时需运用到整体思想,求解时,将所求代数式的一部分看作一个整体,再用整体思想代入求值.
探究新知
2.已知关于x的一元二次方程x2+ax+a=0的一个根是3,求a的值.
解:由题意把x=3代入方程x2+ax+a=0,得
32+3a+a=0
9+4a=0
4a=-9
1.已知方程5x +mx-6=0的一个根为4,则m的值为_______.
练一练
一元二次方程的解的估算
幼儿园活动教室矩形地面的长为8米,宽为5米,现准备在地面的正中间铺设一块面积为18m2的地毯,四周未铺地毯的条形区域的宽度都相同
,你能求出这个宽度吗?
四周未铺地毯部分的宽度x满足方程:
(8-2x)(5-2x)=18
化简
,得
2x2-13x+11=0
你能确定x的大致范围吗?
探究新知
方程(8-2x)(5-2x)=18
(1)x可能小于0吗
x可能大于4吗
可能大于2.5吗
(2)你能确定x的大致范围吗?
宽度x不可能小于0,
没有意义
不可能,(8-2x)>0
不可能,
(5-2x)>0
0
<
x
<2.5
8-2x
5-2x
探究新知
方程(8-2x)(5-2x)=18
(3)填写下表:
x
0.5
1
1.5
2
(8-2x)(5-2x)
28
18
15
4
当x=1时,(8-2x)(5-2x)=18,∴方程的解为x=1
方程的解为x=1
探究新知
步骤:
①在未知数x的取值范围内确定范围;
②根据题意的具体情况再次确定大致范围;
③列出未知数的取值和方程的值的表格进行再次确定;
④最终得出未知数的最小取值范围或具体数据。
一元二次方程解的估算(一)
探究新知
解:梯子的底端滑动的距离x满足方程:
72+(x+6)2=102
10m
8m
1m
xm
你能确定滑动距离x的大致范围吗?
如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?
化简:
x +12x-15
=0
探究新知
(1)小明认为底端也滑动了1m,他的说法正确吗 为什么
(2)底端滑动的距离可能是2
m吗 可能是3
m吗 为什么
(3)你能确定x的大致范围吗?
(4)x的整数部分是几 十分位是几
方程
x +12x-15
=0
(1)当x=1时,x +12x-15
=-2
≠0,
∴
x=1不是方程的解
(2)当x=2时,x +12x-15
=13
≠0,
∴
x=2不是方程的解
当x=3时,x +12x-15
=30
≠0,
∴
x=3不是方程的解
(3)
x的大致范围:1<
x<2
探究新知
(1)取值计算,逐步逼近
x
0
0.5
1
1.5
2
…
x2+12x
-
15
-15
-
8.75
-
2
5.25
13
…
∴x取值的大致范围是:1∴
x取值的大致范围是:1.1<x<1.2
x
1.1
1.2
1.3
1.4
x2
+
12x
-
15
-
0.59
0.84
2.29
3.76
(2)保留整数部分不变,找十分位进一步计算:
x +12x-15
=0
x整数部分是1
,十分位部分是1
探究新知
(1)化为一般形式
(2)根据实际情况确定x大体的取值范围。
(3)在x范围内取整数值,能够使方程左边等于0,则这个数就是方程的一个解.
(4)若在x的范围内取值,没有一个数能够使方程的左边等于0,
则找出值最接近于0且小于0的数,这个数就是方程的近似取值。
一元二次方程解的估算(二)
探究新知
1.下列方程中,有一个根为-1的方程是( )
A.x2-x=0
B.x2-6x+5=0
C.x2-3x-4=0
D.2x2+3x-5=0
C
2.若关于x的一元二次方程x2-x-m=0的一个根是x=1,则m的值是( )
A.1
B.
0
C.-1
D.
2
B
课堂练习
C
3.根据下列表格的对应值,判断方程ax2+bx+c=0(a
≠0)的一个解x的范围是(
)
A.
3B.
3.23C.
3.24D.
3.25x
3.23
3.24
3.25
3.26
ax2+bx+c
-0.06
-0.02
0.03
0.09
课堂练习
4.若关于x的一元二次方程(m+2)x2+5x+m2-4=0
有一个根为0,求m的值.
二次项系数不为零不容忽视
解:将x=0代入方程m2-4=0,
解得m=
±2.
∵
m+2
≠0,
∴
m
≠-2,
综上所述:m
=2.
课堂练习
5.五个连续整数,前三个数的平方和等于后两个数的平方和,求这五个整数.
解:设这五个连续整数为x,x+1,x+2,x+3,x+4,
则:
x2+(x+1)2+(x+2)2=(x+3)2+(x+4)2
整理,得:
x2-8x-20=0
x
-3
-2
-1
...
9
10
11
x2-8x-20
13
0
-11
...
-11
0
13
所以,x=-2或x=10.
因此,这五个整数为-2,-1,0,1,2;或10,11,12,13,14,15.
课堂练习
6.一个面积为120米2的矩形苗圃,它的长比宽多2米,求苗圃的长和宽各是多少米
解:设矩形苗圃的宽为x米,则长为(x+2)米,
根据题意得:x(x+2)=120
即:x2+2x-120=0.
x
8
9
10
11
12
x2+2x-120
-40
-21
0
23
48
所以,矩形苗圃的宽为10m,长为12m.
课堂练习
7.一名跳水运动员进行10m跳台跳水训练,在正常情况下,运动员必须在距水面5m以前完成规定的动作,并且调整好入水姿势,否则就容易出现失误,根据经验,运动员起跳后的时间t(s)与运动员距离水面的高度h(m)满足关系式:h=10+2.5t 5t2,那么运动员最多有多长时间完成规定动作
解:根据题意得:10+2.5t-5t=5
即:2t2-t-2=0.
t
0
1
2
3
2t2-t-2
-2
-1
4
13
因此,1课堂练习
解:根据题意得:10+2.5t-5t=5
即:2t2-t-2=0.
t
0
1
2
3
2t2-t-2
-2
-1
4
13
因此,1进一步计算:
t
1.1
1.2
1.3
1.4
2t2-t-2
-0.68
-0.32
0.08
0.52
因此,1.2所以,运动员完成规定动作的时间最多不超过1.3s.
课堂练习
课堂小结
解一元二次方程
(“两边夹”方法)
确定其解的大致范围
列表、计算
进行两边“夹逼”
……
求得近似解
https://www.21cnjy.com/help/help_extract.php
2.1.2
认识一元二次方程(2)
第二章
一元二次方程
2021-2022学年九年级数学上册同步(北师版)
学习目标
1.会进行简单的一元二次方程的试解.
2.根据题意判定一个数是否是一元二次方程的根及利用试解方法解决一些具体问题.
3.理解方程的解的概念,培养有条理的思考与表达的能力.
导入新课
一元二次方程的概念
一元二次方程的一般形式
②含未知数项的最高次数是2;
①只含有一个未知数;
③整式方程.
二次项
一次项
常数项
二次项系数
一次项系数
一元二次方程的解
一元二次方程的根:
使一元二次方程等号两边相等的未知数的值叫作一元二次方程的解(根).
想想:下面哪些数是方程
x2
–
x
–
6
=
0
的解
-3
,
-2
,-1
,0
,1,2,3
解:当x=3时,
x2
–
x
–
6
=9-3-6=
0
当x=-2时,
x2
–
x
–
6
=4+2-6=
0
∴
x=3或x=-2都是x2
–
x
–
6
=
0的解
注意,一元二次方程可能不止一个根.
探究新知
例1:已知a是方程
x2+2x-2=0
的一个实数根,
求
2a2+4a+2018的值.
解:由题意得
方法点拨:求代数式的值,先把已知解代入,再注意观察,有时需运用到整体思想,求解时,将所求代数式的一部分看作一个整体,再用整体思想代入求值.
探究新知
2.已知关于x的一元二次方程x2+ax+a=0的一个根是3,求a的值.
解:由题意把x=3代入方程x2+ax+a=0,得
32+3a+a=0
9+4a=0
4a=-9
1.已知方程5x +mx-6=0的一个根为4,则m的值为_______.
练一练
一元二次方程的解的估算
幼儿园活动教室矩形地面的长为8米,宽为5米,现准备在地面的正中间铺设一块面积为18m2的地毯,四周未铺地毯的条形区域的宽度都相同
,你能求出这个宽度吗?
四周未铺地毯部分的宽度x满足方程:
(8-2x)(5-2x)=18
化简
,得
2x2-13x+11=0
你能确定x的大致范围吗?
探究新知
方程(8-2x)(5-2x)=18
(1)x可能小于0吗
x可能大于4吗
可能大于2.5吗
(2)你能确定x的大致范围吗?
宽度x不可能小于0,
没有意义
不可能,(8-2x)>0
不可能,
(5-2x)>0
0
<
x
<2.5
8-2x
5-2x
探究新知
方程(8-2x)(5-2x)=18
(3)填写下表:
x
0.5
1
1.5
2
(8-2x)(5-2x)
28
18
15
4
当x=1时,(8-2x)(5-2x)=18,∴方程的解为x=1
方程的解为x=1
探究新知
步骤:
①在未知数x的取值范围内确定范围;
②根据题意的具体情况再次确定大致范围;
③列出未知数的取值和方程的值的表格进行再次确定;
④最终得出未知数的最小取值范围或具体数据。
一元二次方程解的估算(一)
探究新知
解:梯子的底端滑动的距离x满足方程:
72+(x+6)2=102
10m
8m
1m
xm
你能确定滑动距离x的大致范围吗?
如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?
化简:
x +12x-15
=0
探究新知
(1)小明认为底端也滑动了1m,他的说法正确吗 为什么
(2)底端滑动的距离可能是2
m吗 可能是3
m吗 为什么
(3)你能确定x的大致范围吗?
(4)x的整数部分是几 十分位是几
方程
x +12x-15
=0
(1)当x=1时,x +12x-15
=-2
≠0,
∴
x=1不是方程的解
(2)当x=2时,x +12x-15
=13
≠0,
∴
x=2不是方程的解
当x=3时,x +12x-15
=30
≠0,
∴
x=3不是方程的解
(3)
x的大致范围:1<
x<2
探究新知
(1)取值计算,逐步逼近
x
0
0.5
1
1.5
2
…
x2+12x
-
15
-15
-
8.75
-
2
5.25
13
…
∴x取值的大致范围是:1
x取值的大致范围是:1.1<x<1.2
x
1.1
1.2
1.3
1.4
x2
+
12x
-
15
-
0.59
0.84
2.29
3.76
(2)保留整数部分不变,找十分位进一步计算:
x +12x-15
=0
x整数部分是1
,十分位部分是1
探究新知
(1)化为一般形式
(2)根据实际情况确定x大体的取值范围。
(3)在x范围内取整数值,能够使方程左边等于0,则这个数就是方程的一个解.
(4)若在x的范围内取值,没有一个数能够使方程的左边等于0,
则找出值最接近于0且小于0的数,这个数就是方程的近似取值。
一元二次方程解的估算(二)
探究新知
1.下列方程中,有一个根为-1的方程是( )
A.x2-x=0
B.x2-6x+5=0
C.x2-3x-4=0
D.2x2+3x-5=0
C
2.若关于x的一元二次方程x2-x-m=0的一个根是x=1,则m的值是( )
A.1
B.
0
C.-1
D.
2
B
课堂练习
C
3.根据下列表格的对应值,判断方程ax2+bx+c=0(a
≠0)的一个解x的范围是(
)
A.
3
3.23
3.24
3.25
3.23
3.24
3.25
3.26
ax2+bx+c
-0.06
-0.02
0.03
0.09
课堂练习
4.若关于x的一元二次方程(m+2)x2+5x+m2-4=0
有一个根为0,求m的值.
二次项系数不为零不容忽视
解:将x=0代入方程m2-4=0,
解得m=
±2.
∵
m+2
≠0,
∴
m
≠-2,
综上所述:m
=2.
课堂练习
5.五个连续整数,前三个数的平方和等于后两个数的平方和,求这五个整数.
解:设这五个连续整数为x,x+1,x+2,x+3,x+4,
则:
x2+(x+1)2+(x+2)2=(x+3)2+(x+4)2
整理,得:
x2-8x-20=0
x
-3
-2
-1
...
9
10
11
x2-8x-20
13
0
-11
...
-11
0
13
所以,x=-2或x=10.
因此,这五个整数为-2,-1,0,1,2;或10,11,12,13,14,15.
课堂练习
6.一个面积为120米2的矩形苗圃,它的长比宽多2米,求苗圃的长和宽各是多少米
解:设矩形苗圃的宽为x米,则长为(x+2)米,
根据题意得:x(x+2)=120
即:x2+2x-120=0.
x
8
9
10
11
12
x2+2x-120
-40
-21
0
23
48
所以,矩形苗圃的宽为10m,长为12m.
课堂练习
7.一名跳水运动员进行10m跳台跳水训练,在正常情况下,运动员必须在距水面5m以前完成规定的动作,并且调整好入水姿势,否则就容易出现失误,根据经验,运动员起跳后的时间t(s)与运动员距离水面的高度h(m)满足关系式:h=10+2.5t 5t2,那么运动员最多有多长时间完成规定动作
解:根据题意得:10+2.5t-5t=5
即:2t2-t-2=0.
t
0
1
2
3
2t2-t-2
-2
-1
4
13
因此,1
解:根据题意得:10+2.5t-5t=5
即:2t2-t-2=0.
t
0
1
2
3
2t2-t-2
-2
-1
4
13
因此,1
t
1.1
1.2
1.3
1.4
2t2-t-2
-0.68
-0.32
0.08
0.52
因此,1.2
课堂练习
课堂小结
解一元二次方程
(“两边夹”方法)
确定其解的大致范围
列表、计算
进行两边“夹逼”
……
求得近似解
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
