2021-2022学年冀教版九年级数学上册28.4垂径定理同步练习(Word版,含答案解析)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学上册28.4垂径定理同步练习(Word版,含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 524.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 10:03:59 | ||
图片预览

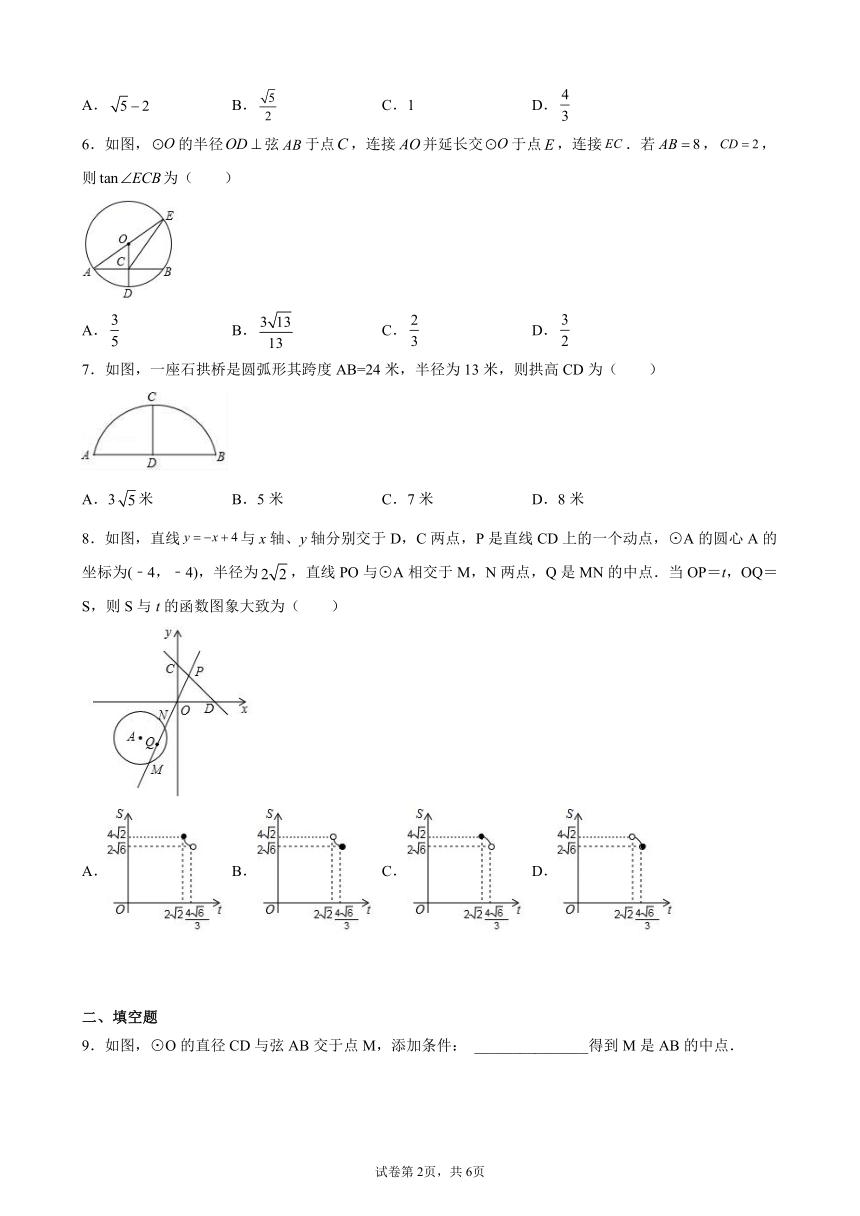
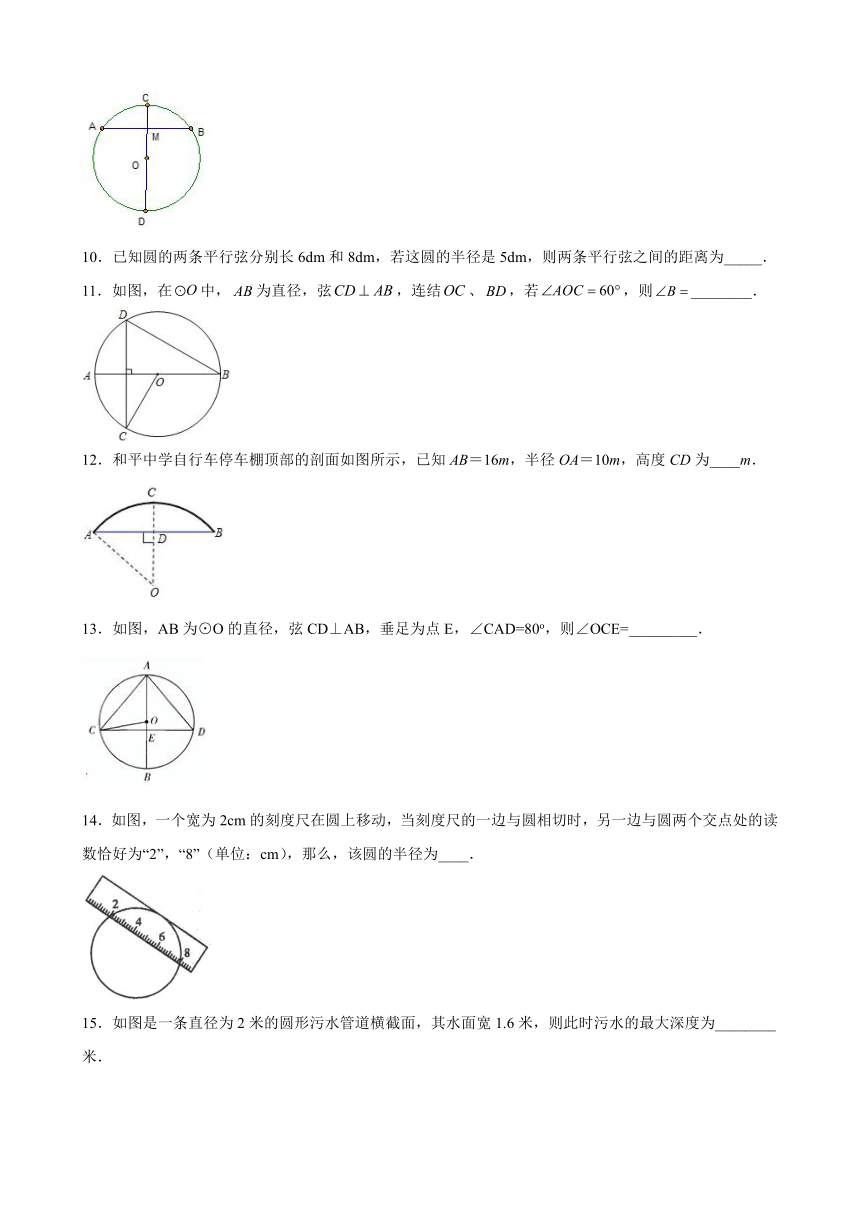
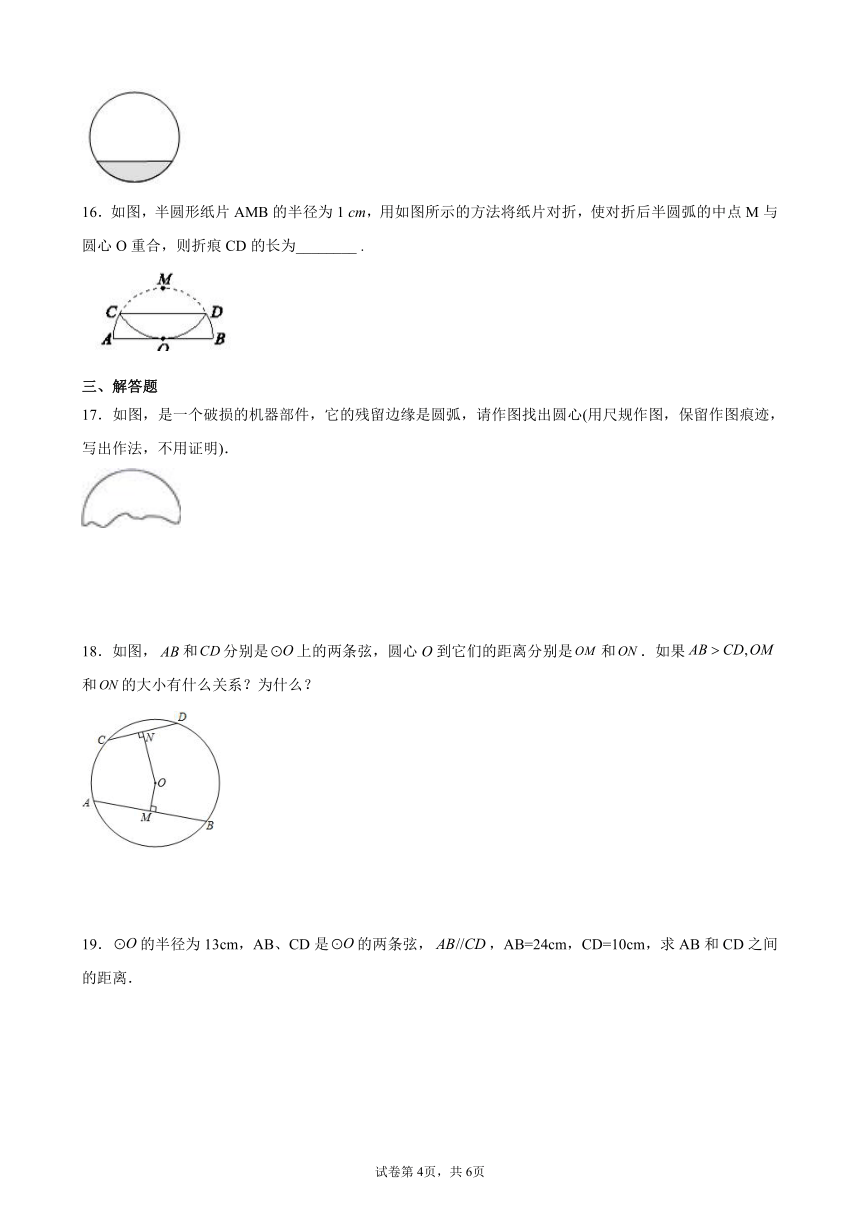

文档简介
2021-2022学年九年级数学上册(冀教版)
28.4垂径定理-同步练习
时间:60分钟
一、单选题
1.下列说法正确的是(
)
A.垂直于弦的直线平分弦所对的两条弧
B.平分弦的直径垂直于弦
C.垂直于直径的弦平分这条直径
D.弦的垂直平分线经过圆心
2.如图,是的直径,弦于点,连接、,下列结论中不一定正确的是(
)
A.
B.
C.
D.
3.如图是一个圆弧形门拱,拱高AB=1,跨度CD=6,那么这个门拱的半径为(
)
A.2m
B.2.5m
C.3m
D.5m
4.如图,AB是⊙O的直径,弦CD⊥AB于点E,连接OC、BD,若∠AOC=110°,则∠ABD的度数是( )
A.35°
B.46°
C.55°
D.70°
5.一种花边由如图的弓形组成,弧ACB的半径为,弦AB=2,则弓形的高CD为(
)
A.
B.
C.1
D.
6.如图,的半径弦于点,连接并延长交于点,连接.若,,则为(
)
A.
B.
C.
D.
7.如图,一座石拱桥是圆弧形其跨度AB=24米,半径为13米,则拱高CD为( )
A.3米
B.5米
C.7米
D.8米
8.如图,直线与x轴、y轴分别交于D,C两点,P是直线CD上的一个动点,⊙A的圆心A的坐标为(﹣4,﹣4),半径为,直线PO与⊙A相交于M,N两点,Q是MN的中点.当OP=t,OQ=S,则S与t的函数图象大致为(
)
A.
B.
C.
D.
二、填空题
9.如图,⊙O的直径CD与弦AB交于点M,添加条件:
_______________得到M是AB的中点.
10.已知圆的两条平行弦分别长6dm和8dm,若这圆的半径是5dm,则两条平行弦之间的距离为_____.
11.如图,在中,为直径,弦,连结、,若,则________.
12.和平中学自行车停车棚顶部的剖面如图所示,已知AB=16m,半径OA=10m,高度CD为____m.
13.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,∠CAD=80o,则∠OCE=_________.
14.如图,一个宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”,“8”(单位:cm),那么,该圆的半径为____.
15.如图是一条直径为2米的圆形污水管道横截面,其水面宽1.6米,则此时污水的最大深度为________米.
16.如图,半圆形纸片AMB的半径为1
cm,用如图所示的方法将纸片对折,使对折后半圆弧的中点M与圆心O重合,则折痕CD的长为________
.
三、解答题
17.如图,是一个破损的机器部件,它的残留边缘是圆弧,请作图找出圆心(用尺规作图,保留作图痕迹,写出作法,不用证明).
18.如图,和分别是上的两条弦,圆心O到它们的距离分别是和.如果和的大小有什么关系?为什么?
19.的半径为13cm,AB、CD是的两条弦,,AB=24cm,CD=10cm,求AB和CD之间的距离.
20.如图,中,P是的中点,C、D是、的中点,过C、D的直线交于E、F.求证:.
21.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
求证:AC=BD.
22.如图,铁路和公路在点O处交会,,在点A处有一栋居民楼,.如果火车行驶时,周围以内会受到噪声的影响,那么火车在铁路上沿方向行驶时,居民楼是否会受到噪声的影响?如果火车行驶的速度为.居民楼受噪声影响的时间约为多少秒(结果保留小数点后一位)?
23.如下图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分.如果M是中弦的中点,经过圆心O交圆O于点E,并且.求的半径.
24.如图,一条公路的转弯处是一段圆弧,点O是这段弧所在圆的圆心,AB=300m,C是上一点,OC⊥AB,垂足为D,CD=45m.求这段弯路的半径.
试卷第1页,共3页
参考答案
1.D
【解析】解:A.垂直于弦的直径平分弦所对的两条弧,所以A选项错误;
B.平分弦(非直径)的直径垂直于弦,所以B选项错误;
C.垂直于直径的弦被这条直径平分,所以C选项错误;
D.弦的垂直平分线经过圆心,所以D选项正确.
故选D.
2.C
【解析】∵直径垂直于弦于点,则由垂径定理可得,,,,故选项A,B,D正确;无法得出,故C错误.
故选C.
3.B
【解析】略
4.C
【解析】连接BC,
∵∠AOC=110°,
∴根据圆周角定理得:∠ABC=∠AOC═55°.
∵CD⊥AB,
∴根据垂径定理得:,
∴∠ABD=∠ABC=55°,
故选:C.
5.A
【解析】解:如图所示:
∵AB⊥CD,
∴根据垂径定理可得:,
由于圆的半径为,
根据勾股定理可得:,
;
故选:A.
6.D
【解析】连接,如图:
∵,∴,设,则,在中,∵,
∴,解得,
∴,∵是直径,∴,
∵是的中位线,∴,
∴.
故选:D.
7.D
【解析】设O为圆心,连接OA、OD,
由题意可知:OD⊥AB,OA=13
由垂径定理可知:AD=AB=12,
∴由勾股定理可知:OD=5,
∴CD=OC﹣CD=8.
故选D.
8.A
【解析】解:连接AO,并延长交直线CD于G,连接AQ,
∵Q是MN的中点,
∴AQ⊥MN,
∵A的坐标为(﹣4,﹣4),
∴直线AO:,,
∵直线CD:,
∴AO⊥CD,
∴∠AQO=∠OGP=90°,
∵∠AOQ=∠POG,
∴,
∴,
当x=0时,y=4,当y=0时,x=4,
∴,,
∴OC=OD=4,
∴OG=CD=,
∵OP=t,OQ=S,
∴,
∴,
故选项C、D不正确;
当OP=时,即S=OQ=,t=,直线OP过圆心A,此时Q与A重合,此种情况成立,
故选项B不正确.
故选:A.
9.CD⊥AB(答案不唯一).
【解析】解:M是弦AB的中点,CD是直径,
由垂径定理可知,CD⊥AB,
故答案为:CD⊥AB(答案不唯一).
10.7dm或1dm
【解析】解:如图,AB∥CD,AB=6dm,CD=8dm,
过O点作OE⊥AB于E,交CD于F点,连OA、OC,
∴AE=BE=AB=3,
∵AB∥CD,EF⊥AB,
∴EF⊥CD,
∴CF=FD=CD=4,
在Rt△OAE中,OA=5dm
OE==4,
同理可得OF=3,
当圆心O在AB与CD之间时,AB与CD的距离=OE+OF=4+3=7(dm);
当圆心O不在AB与CD之间时,AB与CD的距离=OE﹣OF=4﹣3=1(dm).
故答案为7dm或1dm.
11.30°
【解析】连接,根据题意为直径,弦,
由垂径定理可得,
,
.
故答案为:.
12.4.
【解析】解:∵CD⊥AB,AB=16,
∴AD=DB=8,
在Rt△OAD中,AB=16m,半径OA=10m,
∴OD==6,
∴CD=OC﹣OD=10﹣6=4(m).
故答案为4.
13.10°
【解析】∠CAD+∠ACE+∠ADE=180°,∠ACE=∠ADE,解得:∠ACE=50°,∠ACE=∠ACO+∠OCE,根据分析可知:∠ACO=∠CAE=40°,故解得:∠OCE=50°-40°=10°,故答案为10°.
14.cm
【解析】根据题意获得下图:
设OB=r
cm,
∵刻度尺的宽为2cm,
∴OC=r-2,
∵另一边与圆两个交点处的读数恰好为“2”和“8”,
∴BC=×6=3,
在Rt△OBC中,
∵OB2=OC2+BC2,即r2=(r-2)2+32,解得r=
cm.
故答案为cm.
15.0.4
【解析】如图,连接,过点作于点,
∵,米,
∴(米),
∵圆形污水管道的直径为2米,
∴米,
在中,根据勾股定理得,(米),
∴(米).
故答案是0.4.
16.cm
【解析】作MO交CD于E,则MO⊥CD,连接CO,
对折后半圆弧的中点M与圆心O重合,
则ME=OE=OC,
在直角三角形COE中,CE=,
折痕CD的长为2×=(cm).
故答案为cm
17.见解析
【解析】
①在残缺的圆弧上,任选三点,连接相邻的两点;
②作两条线段的垂直平分线,相交于一点.
交点即是圆心的位置.
18.OM<ON,理由见解析
【解析】解:OM<ON.理由如下:
如图所示,连接OC,OA,
∴OA=OC,
∵ON⊥CD,OM⊥AB,
∴CN=CD,AM=AB,
又∵CD<AB,
∴CN<AM,
∴CN2<AM2,
在Rt△OCN和Rt△OAM中,OM2=OA2-AM2,ON2=OC2-CN2,
∴OM2<ON2,
∴OM<ON.
19.7cm或17cm.
【解析】解:①当弦AB和CD在圆心同侧时,如图1
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=12 5=7cm;
②当弦AB和CD在圆心异侧时,如图2,
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=OF+OE=17cm.
∴AB与CD之间的距离为7cm或17cm.
20.证明见详解
【解析】证明:连结OC,OD,OP交EF于G,
∵P是的中点,
∴,
∴AP=BP,
∵C、D是、的中点,
∴OC⊥PA,OD⊥PB,CP=,DP=,
∴∠PCO=∠PDO=90°,CP=DP,
∴OC==OD,
∴OP是CD的垂直平分线,
∴CG=DG,
∵CD在EF上,EF是弦,OP为半径,OP⊥EF,
∴EG=FG,
∴EC=EG-CG=GF-GD=DF.
∴EC=
DF.
21.证明见解析.
【解析】过O作OE⊥AB于点E,
则CE=DE,AE=BE,
∴BE-DE=AE-CE.
即AC=BD.
22.居民楼会受到噪声的影响,17.3s
【解析】解:过点A作AB⊥MN,AB是火车在行驶的过程中,距离居民楼最近的地方,
∵∠QON=30°,AO=200m,
∴AB=OA=200×=100m<200m,
∴居民楼会受到噪音的影响;
∵OA=200m,
∴以A为圆心,OA为半径作圆,交MN于D,
则OA=AD=200(m),
∵AB⊥OD,
∴OB=BD,
∵在Rt△AOB中,OB==100(m),
∴OD=2BO=200(m),
∵火车行驶的速度为72km/h=20m/s,
∴≈17.3(s).
答:居民楼受噪音影响的时间为17.3
s.
23.
【解析】解:连接CO.∵M是弦CD的中点,且EM经过圆心O,
∴EM⊥CD,且CM=CD=×4=2.
在Rt△OCM中,令⊙O的半径为rm,
∵OC2=OM2+CM2,
∴,
解得:r=.
24.272.5m
【解析】解:设这段弯路的半径为r m,
∵OC⊥AB于D,AB=300(m),
∴BD=DA=AB=150(m),
∵CD=45(m),
得OD=r-45(m).
∵Rt△BOD中,根据勾股定理有BO2=BD2+DO2,
即r2=1502+(r-45)2,
解得r=272.5(m).
答:这段弯路的半径为272.5 m.
答案第1页,共2页
答案第1页,共2页
28.4垂径定理-同步练习
时间:60分钟
一、单选题
1.下列说法正确的是(
)
A.垂直于弦的直线平分弦所对的两条弧
B.平分弦的直径垂直于弦
C.垂直于直径的弦平分这条直径
D.弦的垂直平分线经过圆心
2.如图,是的直径,弦于点,连接、,下列结论中不一定正确的是(
)
A.
B.
C.
D.
3.如图是一个圆弧形门拱,拱高AB=1,跨度CD=6,那么这个门拱的半径为(
)
A.2m
B.2.5m
C.3m
D.5m
4.如图,AB是⊙O的直径,弦CD⊥AB于点E,连接OC、BD,若∠AOC=110°,则∠ABD的度数是( )
A.35°
B.46°
C.55°
D.70°
5.一种花边由如图的弓形组成,弧ACB的半径为,弦AB=2,则弓形的高CD为(
)
A.
B.
C.1
D.
6.如图,的半径弦于点,连接并延长交于点,连接.若,,则为(
)
A.
B.
C.
D.
7.如图,一座石拱桥是圆弧形其跨度AB=24米,半径为13米,则拱高CD为( )
A.3米
B.5米
C.7米
D.8米
8.如图,直线与x轴、y轴分别交于D,C两点,P是直线CD上的一个动点,⊙A的圆心A的坐标为(﹣4,﹣4),半径为,直线PO与⊙A相交于M,N两点,Q是MN的中点.当OP=t,OQ=S,则S与t的函数图象大致为(
)
A.
B.
C.
D.
二、填空题
9.如图,⊙O的直径CD与弦AB交于点M,添加条件:
_______________得到M是AB的中点.
10.已知圆的两条平行弦分别长6dm和8dm,若这圆的半径是5dm,则两条平行弦之间的距离为_____.
11.如图,在中,为直径,弦,连结、,若,则________.
12.和平中学自行车停车棚顶部的剖面如图所示,已知AB=16m,半径OA=10m,高度CD为____m.
13.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,∠CAD=80o,则∠OCE=_________.
14.如图,一个宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”,“8”(单位:cm),那么,该圆的半径为____.
15.如图是一条直径为2米的圆形污水管道横截面,其水面宽1.6米,则此时污水的最大深度为________米.
16.如图,半圆形纸片AMB的半径为1
cm,用如图所示的方法将纸片对折,使对折后半圆弧的中点M与圆心O重合,则折痕CD的长为________
.
三、解答题
17.如图,是一个破损的机器部件,它的残留边缘是圆弧,请作图找出圆心(用尺规作图,保留作图痕迹,写出作法,不用证明).
18.如图,和分别是上的两条弦,圆心O到它们的距离分别是和.如果和的大小有什么关系?为什么?
19.的半径为13cm,AB、CD是的两条弦,,AB=24cm,CD=10cm,求AB和CD之间的距离.
20.如图,中,P是的中点,C、D是、的中点,过C、D的直线交于E、F.求证:.
21.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
求证:AC=BD.
22.如图,铁路和公路在点O处交会,,在点A处有一栋居民楼,.如果火车行驶时,周围以内会受到噪声的影响,那么火车在铁路上沿方向行驶时,居民楼是否会受到噪声的影响?如果火车行驶的速度为.居民楼受噪声影响的时间约为多少秒(结果保留小数点后一位)?
23.如下图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分.如果M是中弦的中点,经过圆心O交圆O于点E,并且.求的半径.
24.如图,一条公路的转弯处是一段圆弧,点O是这段弧所在圆的圆心,AB=300m,C是上一点,OC⊥AB,垂足为D,CD=45m.求这段弯路的半径.
试卷第1页,共3页
参考答案
1.D
【解析】解:A.垂直于弦的直径平分弦所对的两条弧,所以A选项错误;
B.平分弦(非直径)的直径垂直于弦,所以B选项错误;
C.垂直于直径的弦被这条直径平分,所以C选项错误;
D.弦的垂直平分线经过圆心,所以D选项正确.
故选D.
2.C
【解析】∵直径垂直于弦于点,则由垂径定理可得,,,,故选项A,B,D正确;无法得出,故C错误.
故选C.
3.B
【解析】略
4.C
【解析】连接BC,
∵∠AOC=110°,
∴根据圆周角定理得:∠ABC=∠AOC═55°.
∵CD⊥AB,
∴根据垂径定理得:,
∴∠ABD=∠ABC=55°,
故选:C.
5.A
【解析】解:如图所示:
∵AB⊥CD,
∴根据垂径定理可得:,
由于圆的半径为,
根据勾股定理可得:,
;
故选:A.
6.D
【解析】连接,如图:
∵,∴,设,则,在中,∵,
∴,解得,
∴,∵是直径,∴,
∵是的中位线,∴,
∴.
故选:D.
7.D
【解析】设O为圆心,连接OA、OD,
由题意可知:OD⊥AB,OA=13
由垂径定理可知:AD=AB=12,
∴由勾股定理可知:OD=5,
∴CD=OC﹣CD=8.
故选D.
8.A
【解析】解:连接AO,并延长交直线CD于G,连接AQ,
∵Q是MN的中点,
∴AQ⊥MN,
∵A的坐标为(﹣4,﹣4),
∴直线AO:,,
∵直线CD:,
∴AO⊥CD,
∴∠AQO=∠OGP=90°,
∵∠AOQ=∠POG,
∴,
∴,
当x=0时,y=4,当y=0时,x=4,
∴,,
∴OC=OD=4,
∴OG=CD=,
∵OP=t,OQ=S,
∴,
∴,
故选项C、D不正确;
当OP=时,即S=OQ=,t=,直线OP过圆心A,此时Q与A重合,此种情况成立,
故选项B不正确.
故选:A.
9.CD⊥AB(答案不唯一).
【解析】解:M是弦AB的中点,CD是直径,
由垂径定理可知,CD⊥AB,
故答案为:CD⊥AB(答案不唯一).
10.7dm或1dm
【解析】解:如图,AB∥CD,AB=6dm,CD=8dm,
过O点作OE⊥AB于E,交CD于F点,连OA、OC,
∴AE=BE=AB=3,
∵AB∥CD,EF⊥AB,
∴EF⊥CD,
∴CF=FD=CD=4,
在Rt△OAE中,OA=5dm
OE==4,
同理可得OF=3,
当圆心O在AB与CD之间时,AB与CD的距离=OE+OF=4+3=7(dm);
当圆心O不在AB与CD之间时,AB与CD的距离=OE﹣OF=4﹣3=1(dm).
故答案为7dm或1dm.
11.30°
【解析】连接,根据题意为直径,弦,
由垂径定理可得,
,
.
故答案为:.
12.4.
【解析】解:∵CD⊥AB,AB=16,
∴AD=DB=8,
在Rt△OAD中,AB=16m,半径OA=10m,
∴OD==6,
∴CD=OC﹣OD=10﹣6=4(m).
故答案为4.
13.10°
【解析】∠CAD+∠ACE+∠ADE=180°,∠ACE=∠ADE,解得:∠ACE=50°,∠ACE=∠ACO+∠OCE,根据分析可知:∠ACO=∠CAE=40°,故解得:∠OCE=50°-40°=10°,故答案为10°.
14.cm
【解析】根据题意获得下图:
设OB=r
cm,
∵刻度尺的宽为2cm,
∴OC=r-2,
∵另一边与圆两个交点处的读数恰好为“2”和“8”,
∴BC=×6=3,
在Rt△OBC中,
∵OB2=OC2+BC2,即r2=(r-2)2+32,解得r=
cm.
故答案为cm.
15.0.4
【解析】如图,连接,过点作于点,
∵,米,
∴(米),
∵圆形污水管道的直径为2米,
∴米,
在中,根据勾股定理得,(米),
∴(米).
故答案是0.4.
16.cm
【解析】作MO交CD于E,则MO⊥CD,连接CO,
对折后半圆弧的中点M与圆心O重合,
则ME=OE=OC,
在直角三角形COE中,CE=,
折痕CD的长为2×=(cm).
故答案为cm
17.见解析
【解析】
①在残缺的圆弧上,任选三点,连接相邻的两点;
②作两条线段的垂直平分线,相交于一点.
交点即是圆心的位置.
18.OM<ON,理由见解析
【解析】解:OM<ON.理由如下:
如图所示,连接OC,OA,
∴OA=OC,
∵ON⊥CD,OM⊥AB,
∴CN=CD,AM=AB,
又∵CD<AB,
∴CN<AM,
∴CN2<AM2,
在Rt△OCN和Rt△OAM中,OM2=OA2-AM2,ON2=OC2-CN2,
∴OM2<ON2,
∴OM<ON.
19.7cm或17cm.
【解析】解:①当弦AB和CD在圆心同侧时,如图1
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=12 5=7cm;
②当弦AB和CD在圆心异侧时,如图2,
∵AB=24cm,CD=10cm,
∴AE=12cm,CF=5cm,
∵OA=OC=13cm,
∴EO=5cm,OF=12cm,
∴EF=OF+OE=17cm.
∴AB与CD之间的距离为7cm或17cm.
20.证明见详解
【解析】证明:连结OC,OD,OP交EF于G,
∵P是的中点,
∴,
∴AP=BP,
∵C、D是、的中点,
∴OC⊥PA,OD⊥PB,CP=,DP=,
∴∠PCO=∠PDO=90°,CP=DP,
∴OC==OD,
∴OP是CD的垂直平分线,
∴CG=DG,
∵CD在EF上,EF是弦,OP为半径,OP⊥EF,
∴EG=FG,
∴EC=EG-CG=GF-GD=DF.
∴EC=
DF.
21.证明见解析.
【解析】过O作OE⊥AB于点E,
则CE=DE,AE=BE,
∴BE-DE=AE-CE.
即AC=BD.
22.居民楼会受到噪声的影响,17.3s
【解析】解:过点A作AB⊥MN,AB是火车在行驶的过程中,距离居民楼最近的地方,
∵∠QON=30°,AO=200m,
∴AB=OA=200×=100m<200m,
∴居民楼会受到噪音的影响;
∵OA=200m,
∴以A为圆心,OA为半径作圆,交MN于D,
则OA=AD=200(m),
∵AB⊥OD,
∴OB=BD,
∵在Rt△AOB中,OB==100(m),
∴OD=2BO=200(m),
∵火车行驶的速度为72km/h=20m/s,
∴≈17.3(s).
答:居民楼受噪音影响的时间为17.3
s.
23.
【解析】解:连接CO.∵M是弦CD的中点,且EM经过圆心O,
∴EM⊥CD,且CM=CD=×4=2.
在Rt△OCM中,令⊙O的半径为rm,
∵OC2=OM2+CM2,
∴,
解得:r=.
24.272.5m
【解析】解:设这段弯路的半径为r m,
∵OC⊥AB于D,AB=300(m),
∴BD=DA=AB=150(m),
∵CD=45(m),
得OD=r-45(m).
∵Rt△BOD中,根据勾股定理有BO2=BD2+DO2,
即r2=1502+(r-45)2,
解得r=272.5(m).
答:这段弯路的半径为272.5 m.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
