2021-2022学年冀教版九年级数学上册28.3圆心角和圆周角同步练习(Word版,含答案解析)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学上册28.3圆心角和圆周角同步练习(Word版,含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 556.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 00:00:00 | ||
图片预览


文档简介
2021-2022学年九年级数学上册(冀教版)
28.3圆心角和圆周角-同步练习
时间:60分钟
一、单选题
1.如图,其中圆周角有(
)
A.1个
B.2个
C.3个
D.4个
2.下图中是圆心角的是(
)
A.
B.
C.
D.
3.如图,是的外接圆,直径,弦,则弦等于(
)
A.6
B.5
C.4
D.8
4.如图所示,A,D是⊙O上的两个点,BC是直径,若∠D=35°,则∠ACB的度数是(
)
A.35°
B.55°
C.65°
D.70°
5.如图,是外一点,,分别交于,两点,已知和所对的圆心角分别为和,则(
)
A.
B.
C.
D.
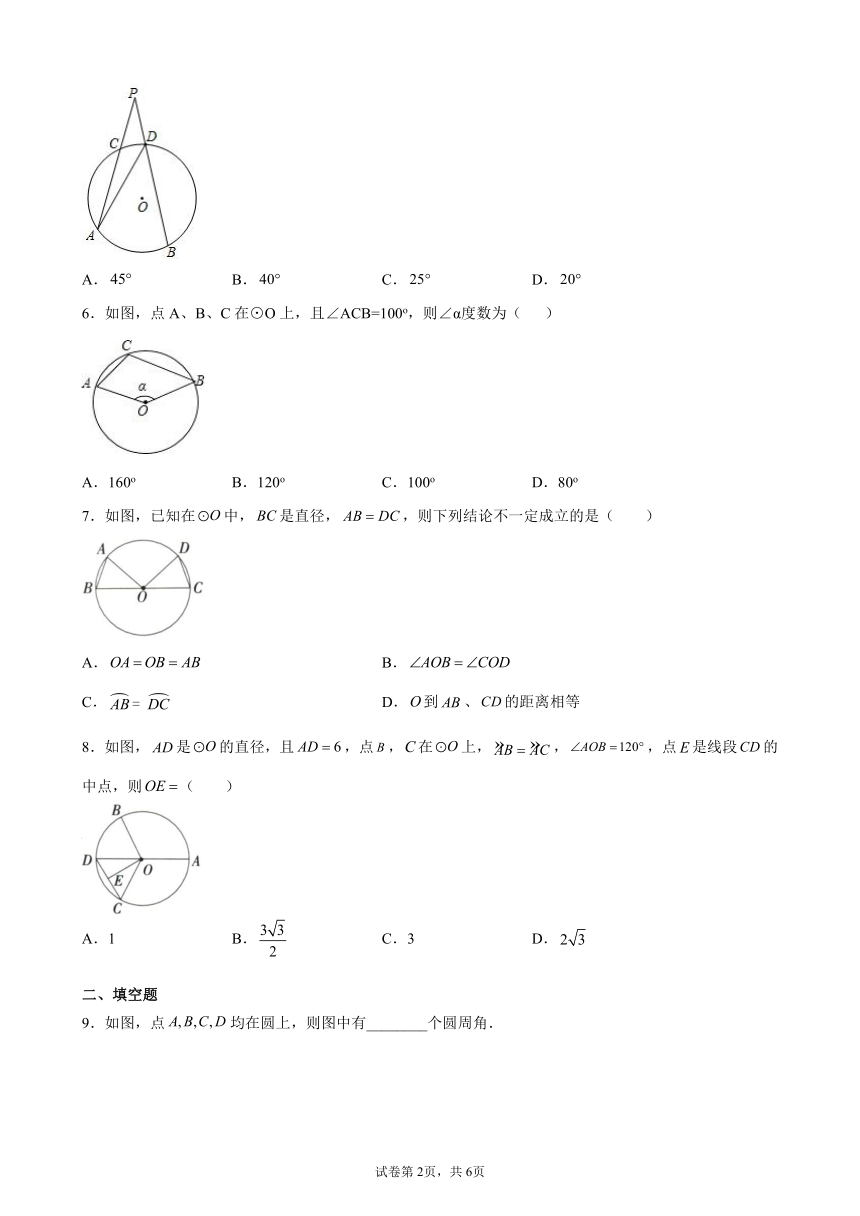
6.如图,点A、B、C在⊙O上,且∠ACB=100o,则∠α度数为(
)
A.160o
B.120o
C.100o
D.80o
7.如图,已知在中,是直径,,则下列结论不一定成立的是(
)
A.
B.
C.
D.到、的距离相等
8.如图,是的直径,且,点,在上,,,点是线段的中点,则(
)
A.1
B.
C.3
D.
二、填空题
9.如图,点均在圆上,则图中有________个圆周角.
10.如图,是的外接圆,,是上的一点,则等于________.
11.如图,是的弦,,则________.
12.如图所示,图中能用字母表示的相等的角有________,其判断依据是_______________.
13.120°的圆心角是360°的_______分之一,它所对的弧是相应圆周长的________分之一.
14.若一条弦把圆周分成的两段弧,则劣弧所对圆心角的度数是________.
15.如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为35°,则的度数是_____.
16.如图,△ABC内接于⊙O,∠ACB=90°,∠ACB的角平分线交⊙O于D.若AC=6,BD=5,则BC的长为_____.
三、解答题
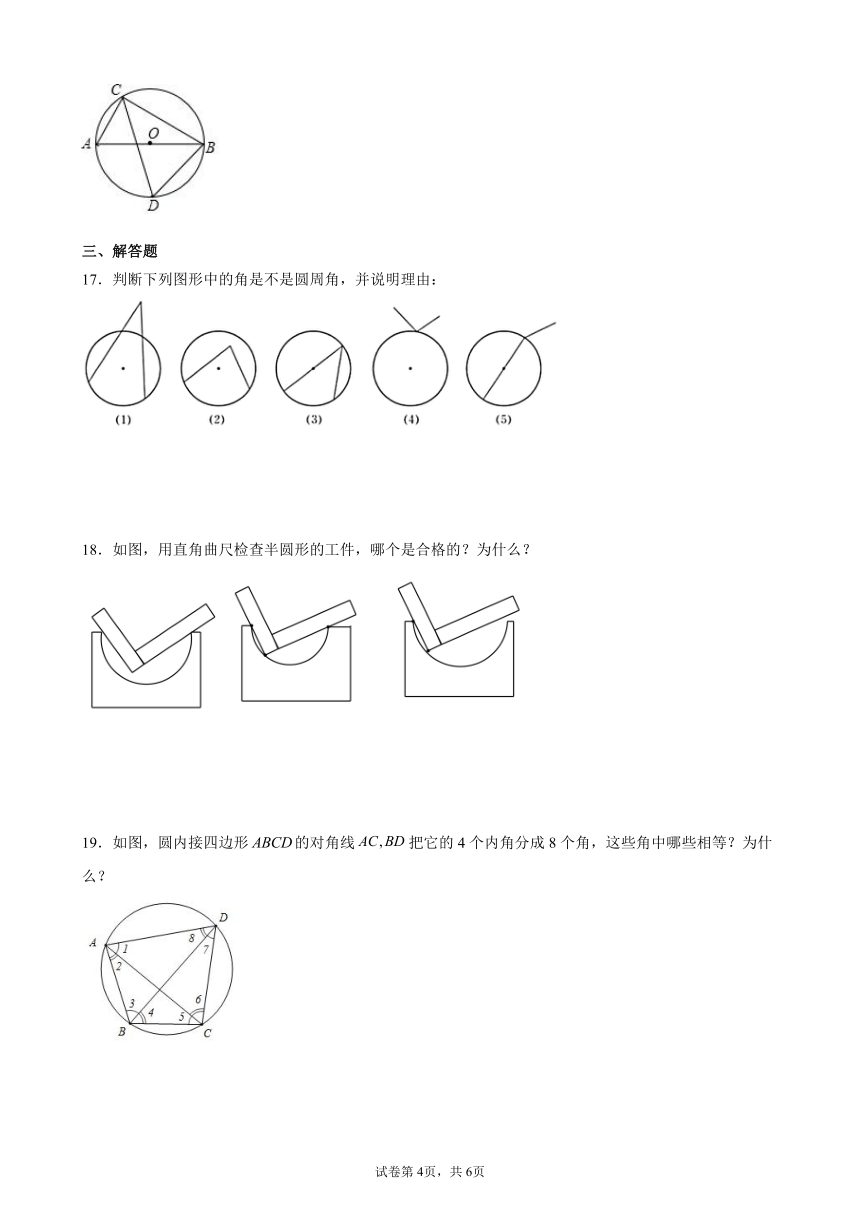
17.判断下列图形中的角是不是圆周角,并说明理由:
18.如图,用直角曲尺检查半圆形的工件,哪个是合格的?为什么?
19.如图,圆内接四边形的对角线把它的4个内角分成8个角,这些角中哪些相等?为什么?
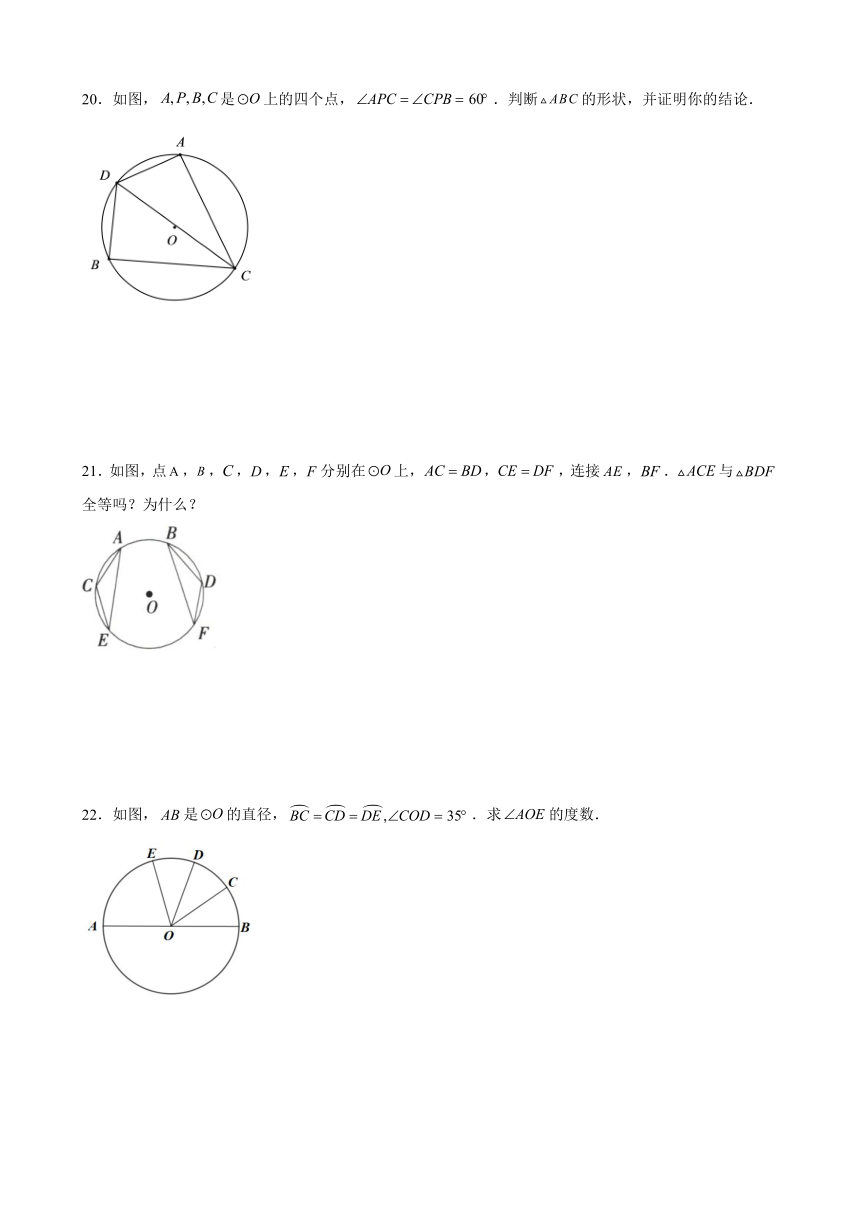
20.如图,是上的四个点,.判断的形状,并证明你的结论.
21.如图,点,,,,,分别在上,,,连接,.与全等吗?为什么?
22.如图,是的直径,.求的度数.
23.某处靠近海岸的海域有一片暗礁,当地海洋管理部门在海岸上建造了两座灯塔,,通告所有船只不要进入以为弦的弓形区域(阴影部分)内(含边界)以免触礁,如图所示.现有一艘货轮正向暗礁区域靠近,当多大时,才能避开暗礁?
24.如图,E是△ABC的内心,AE的延长线交△ABC的外接圆于点D.
(1)BD与DE相等吗?为什么
(2)若∠BAC=90°,DE=4,求△ABC外接圆的半径.
试卷第1页,共3页
参考答案
1.B
【解析】解:根据题意,,是圆周角,共2个.
故选:B.
2.C
【解析】解:A、不是圆心角,故不符合题意;
B、不是圆心角,故不符合题意;
C、是圆心角,故符合题意;
D、不是圆心角,故不符合题意;
故选:C.
3.A
【解析】∵为直径,
∴,
在中,,,
∴,
故选:A.
4.B
【解析】解:连接AB,
由同弧所对的圆周角相等得∠ABC=∠D=35°,
∵BC是⊙O的直径,
∴∠BAC=90°,
∴∠ACB=90°-35°=55°.
故选B.
5.D
【解析】解:如图:连接OC、OD、OA、OB,
∵和所对的圆心角分别为和,
即,,
∴,,
∵,
∴.
故选:D.
6.A
【解析】解:如图,在⊙O取点,连接
四边形为⊙O的内接四边形,
.
故选A
7.A
【解析】在中,弦弦,则其所对圆心角相等,即,所对优弧和劣弧分别相等,所以有,故B项和C项结论正确,
∵,AO=DO=BO=CO
∴(SSS)
可得出点到弦,的距离相等,故D项结论正确;
而由题意不能推出,故A项结论错误.
故选:A
8.B
【解析】∵,,
∴,
∴,
∵,为中点,
∴,,
∵,
∴,
∴,
故选B.
9.8
【解析】解:以点为顶点的圆周角各有1个,以点为顶点的圆周角各有3个,共有8个圆周角.
故答案为8.
10.65°
【解析】解:根据同弧所对的圆周角相等,得
.
∵,
∴.
故答案为:65°
11.
【解析】解:∵,
∴,又,
∴,
故答案为:.
12.和
同弧所对的圆周角相等
【解析】解:由题意可知,
∵和都是对应的圆周角,
和都是对应的圆周角,
∴,
故答案为:和,同弧所对的圆周角相等
13.三
三
【解析】解:120°÷360°=,
它所对的弧是相应圆周长的,
答:120°的圆心角是360°的三分之一,它所对的弧是相应圆周长的三分之一.
故答案为:三;三.
14.
【解析】解:∵一条弦把圆周分成的两段弧,
∴劣弧所对圆心角的度数为,
故答案为:.
15.105°.
【解析】解:连接OD、OE,
∵的度数为35°,
∴∠AOD=35°,
∵CD=CO,
∴∠ODC=∠AOD=35°,
∵OD=OE,
∴∠ODC=∠E=35°,
∴∠DOE=180°-∠ODC-∠E=180°-35°-35°=110°,
∴∠AOE=∠DOE-∠AOD=110°-35°=75°,
∴∠BOE=180°-∠AOE=180°-75°=105°,
∴的度数是105°.
故答案为105°.
16.8
【解析】连接AD,
∵∠ACB=90°,
∴AB是⊙O的直径.
∵∠ACB的角平分线交⊙O于D,
∴∠ACD=∠BCD=45°,
∴AD=BD=5.
∵AB是⊙O的直径,
∴△ABD是等腰直角三角形,
∴AB==10.
∵AC=6,
∴BC==8.
故答案为:8.
17.图(3)是圆周角.图(1)(2)的顶点没有在圆上,图(4)(5)中角的两边没有都与圆相交,都不是圆周角.
【解析】解:图(3)顶点在圆上,并且两边都与圆相交,是圆周角.图(1)(2)的顶点没有在圆上,图(4)(5)中角的两边没有都与圆相交,都不是圆周角.
18.中间的工件是合格的,因为直径所对的圆周角是直角.
【解析】解:由题意可知:中间的工件是合格的,因为直径所对的圆周角是直角,
答:中间的工件是合格的,因为直径所对的圆周角是直角.
19.∠1=∠4,∠2=∠7,∠3=∠6,∠5=∠8;同弧所对的圆周角相等
【解析】解:∵同弧所对的圆周角相等,
∴∠1=∠4,∠2=∠7,∠3=∠6,∠5=∠8.
20.等边三角形,见解析
【解析】解:△ABC是等边三角形.证明如下:
由圆周角定理:∠BAC=∠CPB,∠ABC=∠APC
∵∠APC=∠CPB=60°,
∴∠BAC=∠ABC=60°,
∴∠ACB=180°-∠BAC-∠ABC=180°-60°-60°=60°.
∴△ABC是等边三角形.
21.与全等,见解析
【解析】理由:∵,,
∴,,
∴,即,
∴,
在和中,,
∴.
22.75°
【解析】∵,∠COD=35°,
∴∠BOC=∠EOD=∠COD=35°,
∴∠AOE=180° ∠EOD ∠COD ∠BOC=75°.
23.使∠APB<55°,即在外行驶,就能避开暗礁.
【解析】解:货轮P在航行时,只要使∠APB<55°,即在外行驶,就能避开暗礁.
24.(1)DE=DB,理由见解析;(2)2
【解析】解:(1)DE=DB.
∵AD平分∠BAC,BE平分∠ABC,
∴∠ABE=∠CBE,∠BAE=∠CAD,
∴=,
∴∠DBC=∠CAD,
∴∠DBC=∠BAE,
∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,
∴∠DBE=∠DEB,
∴DE=DB;
(2)连接CD,如图所示:由(1)得:=,
∴CD=BD=DE=4,
∵∠BAC=90°,
∴BC是直径,
∴∠BDC=90°,
∴BC==4,
∴△ABC外接圆的半径:r=2.
答案第1页,共2页
答案第1页,共2页
28.3圆心角和圆周角-同步练习
时间:60分钟
一、单选题
1.如图,其中圆周角有(
)
A.1个
B.2个
C.3个
D.4个
2.下图中是圆心角的是(
)
A.
B.
C.
D.
3.如图,是的外接圆,直径,弦,则弦等于(
)
A.6
B.5
C.4
D.8
4.如图所示,A,D是⊙O上的两个点,BC是直径,若∠D=35°,则∠ACB的度数是(
)
A.35°
B.55°
C.65°
D.70°
5.如图,是外一点,,分别交于,两点,已知和所对的圆心角分别为和,则(
)
A.
B.
C.
D.
6.如图,点A、B、C在⊙O上,且∠ACB=100o,则∠α度数为(
)
A.160o
B.120o
C.100o
D.80o
7.如图,已知在中,是直径,,则下列结论不一定成立的是(
)
A.
B.
C.
D.到、的距离相等
8.如图,是的直径,且,点,在上,,,点是线段的中点,则(
)
A.1
B.
C.3
D.
二、填空题
9.如图,点均在圆上,则图中有________个圆周角.
10.如图,是的外接圆,,是上的一点,则等于________.
11.如图,是的弦,,则________.
12.如图所示,图中能用字母表示的相等的角有________,其判断依据是_______________.
13.120°的圆心角是360°的_______分之一,它所对的弧是相应圆周长的________分之一.
14.若一条弦把圆周分成的两段弧,则劣弧所对圆心角的度数是________.
15.如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为35°,则的度数是_____.
16.如图,△ABC内接于⊙O,∠ACB=90°,∠ACB的角平分线交⊙O于D.若AC=6,BD=5,则BC的长为_____.
三、解答题
17.判断下列图形中的角是不是圆周角,并说明理由:
18.如图,用直角曲尺检查半圆形的工件,哪个是合格的?为什么?
19.如图,圆内接四边形的对角线把它的4个内角分成8个角,这些角中哪些相等?为什么?
20.如图,是上的四个点,.判断的形状,并证明你的结论.
21.如图,点,,,,,分别在上,,,连接,.与全等吗?为什么?
22.如图,是的直径,.求的度数.
23.某处靠近海岸的海域有一片暗礁,当地海洋管理部门在海岸上建造了两座灯塔,,通告所有船只不要进入以为弦的弓形区域(阴影部分)内(含边界)以免触礁,如图所示.现有一艘货轮正向暗礁区域靠近,当多大时,才能避开暗礁?
24.如图,E是△ABC的内心,AE的延长线交△ABC的外接圆于点D.
(1)BD与DE相等吗?为什么
(2)若∠BAC=90°,DE=4,求△ABC外接圆的半径.
试卷第1页,共3页
参考答案
1.B
【解析】解:根据题意,,是圆周角,共2个.
故选:B.
2.C
【解析】解:A、不是圆心角,故不符合题意;
B、不是圆心角,故不符合题意;
C、是圆心角,故符合题意;
D、不是圆心角,故不符合题意;
故选:C.
3.A
【解析】∵为直径,
∴,
在中,,,
∴,
故选:A.
4.B
【解析】解:连接AB,
由同弧所对的圆周角相等得∠ABC=∠D=35°,
∵BC是⊙O的直径,
∴∠BAC=90°,
∴∠ACB=90°-35°=55°.
故选B.
5.D
【解析】解:如图:连接OC、OD、OA、OB,
∵和所对的圆心角分别为和,
即,,
∴,,
∵,
∴.
故选:D.
6.A
【解析】解:如图,在⊙O取点,连接
四边形为⊙O的内接四边形,
.
故选A
7.A
【解析】在中,弦弦,则其所对圆心角相等,即,所对优弧和劣弧分别相等,所以有,故B项和C项结论正确,
∵,AO=DO=BO=CO
∴(SSS)
可得出点到弦,的距离相等,故D项结论正确;
而由题意不能推出,故A项结论错误.
故选:A
8.B
【解析】∵,,
∴,
∴,
∵,为中点,
∴,,
∵,
∴,
∴,
故选B.
9.8
【解析】解:以点为顶点的圆周角各有1个,以点为顶点的圆周角各有3个,共有8个圆周角.
故答案为8.
10.65°
【解析】解:根据同弧所对的圆周角相等,得
.
∵,
∴.
故答案为:65°
11.
【解析】解:∵,
∴,又,
∴,
故答案为:.
12.和
同弧所对的圆周角相等
【解析】解:由题意可知,
∵和都是对应的圆周角,
和都是对应的圆周角,
∴,
故答案为:和,同弧所对的圆周角相等
13.三
三
【解析】解:120°÷360°=,
它所对的弧是相应圆周长的,
答:120°的圆心角是360°的三分之一,它所对的弧是相应圆周长的三分之一.
故答案为:三;三.
14.
【解析】解:∵一条弦把圆周分成的两段弧,
∴劣弧所对圆心角的度数为,
故答案为:.
15.105°.
【解析】解:连接OD、OE,
∵的度数为35°,
∴∠AOD=35°,
∵CD=CO,
∴∠ODC=∠AOD=35°,
∵OD=OE,
∴∠ODC=∠E=35°,
∴∠DOE=180°-∠ODC-∠E=180°-35°-35°=110°,
∴∠AOE=∠DOE-∠AOD=110°-35°=75°,
∴∠BOE=180°-∠AOE=180°-75°=105°,
∴的度数是105°.
故答案为105°.
16.8
【解析】连接AD,
∵∠ACB=90°,
∴AB是⊙O的直径.
∵∠ACB的角平分线交⊙O于D,
∴∠ACD=∠BCD=45°,
∴AD=BD=5.
∵AB是⊙O的直径,
∴△ABD是等腰直角三角形,
∴AB==10.
∵AC=6,
∴BC==8.
故答案为:8.
17.图(3)是圆周角.图(1)(2)的顶点没有在圆上,图(4)(5)中角的两边没有都与圆相交,都不是圆周角.
【解析】解:图(3)顶点在圆上,并且两边都与圆相交,是圆周角.图(1)(2)的顶点没有在圆上,图(4)(5)中角的两边没有都与圆相交,都不是圆周角.
18.中间的工件是合格的,因为直径所对的圆周角是直角.
【解析】解:由题意可知:中间的工件是合格的,因为直径所对的圆周角是直角,
答:中间的工件是合格的,因为直径所对的圆周角是直角.
19.∠1=∠4,∠2=∠7,∠3=∠6,∠5=∠8;同弧所对的圆周角相等
【解析】解:∵同弧所对的圆周角相等,
∴∠1=∠4,∠2=∠7,∠3=∠6,∠5=∠8.
20.等边三角形,见解析
【解析】解:△ABC是等边三角形.证明如下:
由圆周角定理:∠BAC=∠CPB,∠ABC=∠APC
∵∠APC=∠CPB=60°,
∴∠BAC=∠ABC=60°,
∴∠ACB=180°-∠BAC-∠ABC=180°-60°-60°=60°.
∴△ABC是等边三角形.
21.与全等,见解析
【解析】理由:∵,,
∴,,
∴,即,
∴,
在和中,,
∴.
22.75°
【解析】∵,∠COD=35°,
∴∠BOC=∠EOD=∠COD=35°,
∴∠AOE=180° ∠EOD ∠COD ∠BOC=75°.
23.使∠APB<55°,即在外行驶,就能避开暗礁.
【解析】解:货轮P在航行时,只要使∠APB<55°,即在外行驶,就能避开暗礁.
24.(1)DE=DB,理由见解析;(2)2
【解析】解:(1)DE=DB.
∵AD平分∠BAC,BE平分∠ABC,
∴∠ABE=∠CBE,∠BAE=∠CAD,
∴=,
∴∠DBC=∠CAD,
∴∠DBC=∠BAE,
∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,
∴∠DBE=∠DEB,
∴DE=DB;
(2)连接CD,如图所示:由(1)得:=,
∴CD=BD=DE=4,
∵∠BAC=90°,
∴BC是直径,
∴∠BDC=90°,
∴BC==4,
∴△ABC外接圆的半径:r=2.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
