2021-2022学年冀教版九年级数学上册28.5 弧长和扇形面积的计算同步练习(Word版,含答案解析)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学上册28.5 弧长和扇形面积的计算同步练习(Word版,含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 617.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 10:07:46 | ||
图片预览



文档简介
2021-2022学年九年级数学上册(冀教版)
28.5弧长和扇形面积的计算-同步练习
时间:60分钟
一、单选题
1.已知某扇形的半径为6,圆心角的度数为,则扇形的弧长为(
)
A.
B.
C.
D.
2.一个滑轮起重装置如图所示,滑轮的半径是15cm,当重物上升15cn时,滑轮的一条半径OA绕轴心O按顺时针方向旋转的角度约为(
)(π取3.14,结果精确到1 )
A.115
B.60
C.57
D.29
3.如图,在中,,
,.将绕直角顶点逆时针旋转得
,则点转过的路径长为(
)
A.
B.
C.
D.
4.60°的圆心角所对的弧长是3πcm,则此弧所在圆的半径是(
)
A.6cm
B.7cm
C.8cm
D.9cm
5.一张圆心角为的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是(
)
A.
B.
C.
D.
6.如图,在中,,将△AOC绕点O顺时针旋转后得到,则AC边在旋转过程中所扫过的图形的面积为(
).
A.
B.
C.
D.
7.如图,在Rt中,∠BCA=90°
两分圆别以为半径画圆,则阴影部分的面积为(
)
A.
B.
C.
D.
8.如图,在中,,,以的中点为圆心,作圆心角为的扇形,点恰在上,设,当由小到大变化时,图中阴影部分的面积为(
)
A.
B.
C.
D.随的变化而变化
二、填空题
9.已知60°的圆心角所对的弧长为3cm,它所在的圆的周长是_________cm.
10.扇形的弧长和半径都是2,则其面积为________.
11.如图,若长为周长的,则_________.
12.半径为的圆中,的圆心角所对的弧长为__________;弧长为的圆心角约为________.
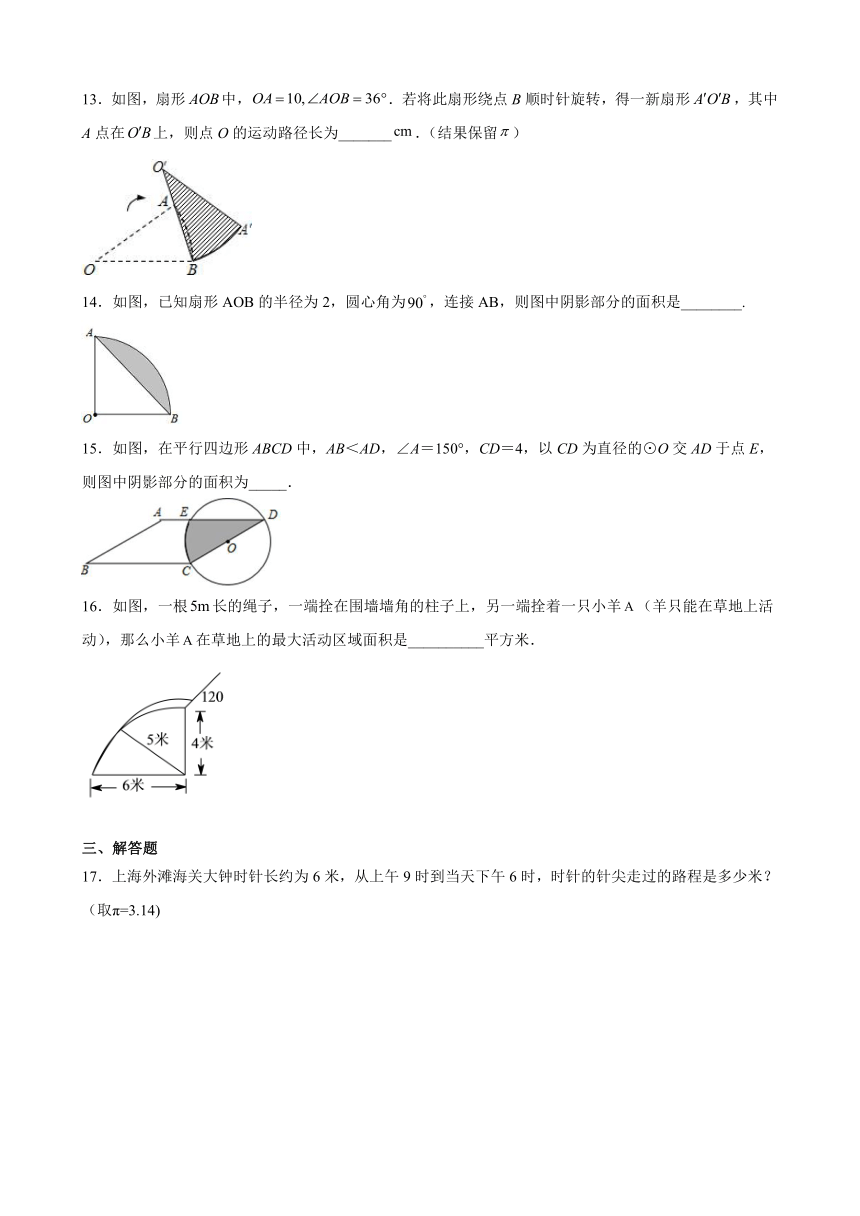
13.如图,扇形中,.若将此扇形绕点B顺时针旋转,得一新扇形,其中A点在上,则点O的运动路径长为_______.(结果保留)
14.如图,已知扇形AOB的半径为2,圆心角为,连接AB,则图中阴影部分的面积是________.
15.如图,在平行四边形ABCD中,AB<AD,∠A=150°,CD=4,以CD为直径的⊙O交AD于点E,则图中阴影部分的面积为_____.
16.如图,一根长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊(羊只能在草地上活动),那么小羊在草地上的最大活动区域面积是__________平方米.
三、解答题
17.上海外滩海关大钟时针长约为6米,从上午9时到当天下午6时,时针的针尖走过的路程是多少米?(取π=3.14)
18.如图,草坪上的自动喷水装置能旋转,它的喷灌区域是一个扇形,这个扇形的半径是.求它能喷灌的草坪的面积.
19.如图,从一块直径是的圆形铁皮上剪出一个圆心角为的扇形,求被剪掉的部分的面积;如果将剪下来的扇形围成一个圆锥,圆锥的底面圆的半径是多少?
20.如图,直线经过点M(1,)和点N(,3),A、B是此直线与坐标轴的交点.以AB为直径作⊙C,求此圆与y轴围成的阴影部分面积.
21.(1)求图(1)中阴影部分的面积(单位:厘米);
(2)如图(2)所示,已知大正方形的边长为10厘米,小正方形的边长为7厘米,求阴影部分面积.(结果保留)
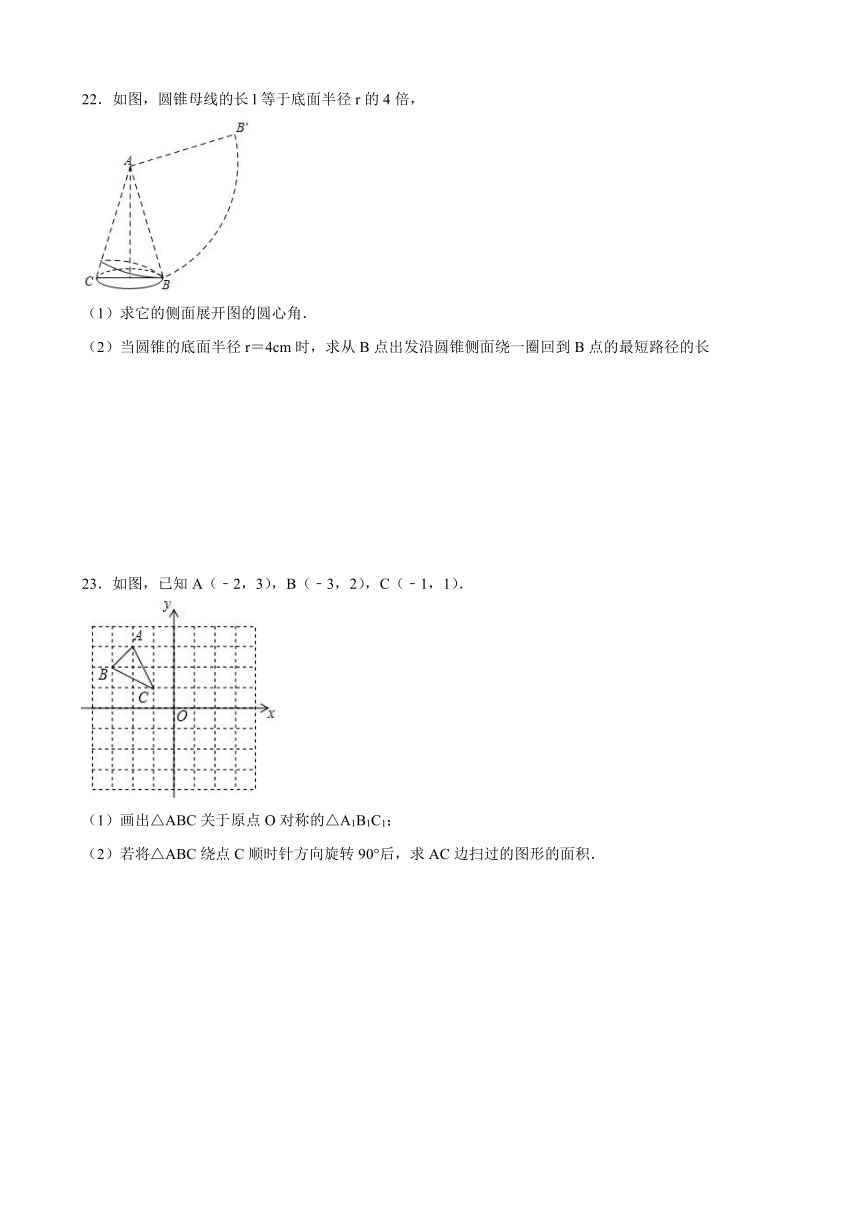
22.如图,圆锥母线的长l等于底面半径r的4倍,
(1)求它的侧面展开图的圆心角.
(2)当圆锥的底面半径r=4cm时,求从B点出发沿圆锥侧面绕一圈回到B点的最短路径的长
23.如图,已知A(﹣2,3),B(﹣3,2),C(﹣1,1).
(1)画出△ABC关于原点O对称的△A1B1C1;
(2)若将△ABC绕点C顺时针方向旋转90°后,求AC边扫过的图形的面积.
试卷第1页,共3页
参考答案
1.C
【解析】∵扇形的半径为6,圆心角的度数为,
∴.
故选C.
2.C
【解析】设OA旋转的角度为n,由于重物上升15
cm,
则点A顺时针旋转的弧长为15
cm,
由弧长公式l=,
可求n=≈57度.
故选C.
3.B
【解析】解:在中,,,
,
,
绕直角顶点逆时针旋转得△,
,
弧的长.
故选:B.
4.D
【解析】∵l,∴r=9(cm).
故选D.
5.A
【解析】解:如图1,连接,
四边形是正方形,
,,
,
,
由勾股定理得:,
扇形的面积是;
如图2,连接、,
四边形是的内接四边形,四边形是正方形,
,,
,
,
,
的面积是,
扇形和圆形纸板的面积比是.
故选:A.
6.B
【解析】解:
∴阴影部分的面积=扇形OAB的面积﹣扇形OCD的面积
故选B.
7.A
【解析】设各个部分的面积为:S1、S2、S3、S4、S5,如图所示,
∵两个半圆的面积和是:S1+S5+S4+S2+S3+S4,△ABC的面积是S3+S4+S5,阴影部分
面积是:S1+S2+S4,
∴图中阴影部分的面积为两个半圆的面积减去三角形的面积.
即阴影部分的面积=π×4+π×1-4×2÷2=π-4.
故选A.
8.C
【解析】如图,连接,作于点,于点,
∵,,∴,
,,∴,
∴四边形是正方形,
∴,∴,
∵,∴,
∴,
在和中,
,
∴,
∴四边形的面积正方形的面积,
∵正方形的面积,
∴四边形的面积,
∵扇形的面积,
∴阴影部分的面积扇形的面积四边形的面积,恒为定值.
故选:C.
9.18
【解析】.
故答案为:18.
10.2
【解析】解:∵扇形的弧长和半径都是2,
∴.
故答案为:2.
11.
【解析】解:设∠AOB=x,圆的半径为r,
∴,圆的周长,
∵弧AB的长是圆周长的,
∴,
∴,
故答案为:.
12.
【解析】,
,
,,
故答案为:,
13.4π.
【解析】解:根据题意,知OA=OB.
又∠AOB=36°,
∴∠OBA=72°.
∴点O旋转至O′点所经过的轨迹长度==4πcm.
故答案是:4π.
14.π-2.
【解析】解:S阴影部分=S扇形OAB-S△OAB
= ×2×2
=π-2
故答案为π-2.
15.
【解析】如图,连接OE,作OF⊥DE于点F,
∵四边形ABCD是平行四边形,且∠A=150°,
∴∠D=30°,
则∠COE=2∠D=60°,
∵CD=4,
∴CO=DO=2,
∴OF=OD=1,DF=ODcos∠ODF=2×=,
∴DE=2DF=2,
∴图中阴影部分的面积为+×2×1=,
故答案为.
16..
【解析】解:如图.小羊的活动范围是:(平方米)
故答案为.
17.28.26m.
【解析】钟时针长为半径,从上午9时到当天下午6时指针走过270度.
所以时针的针尖走过的路程是28.26m.
18.它能喷灌的草坪的面积为m2.
【解析】解:由题意可知喷灌的草坪是一个圆心角为220°,半径为20m的扇形,
∴其面积是S==(m2).
答:它能喷灌的草坪的面积为(m2).
19.被剪掉的部分的面积为m2,圆锥的底面圆的半径是m.
【解析】解:连接AO,BC,
∵∠BAC=90°,
∴BC是⊙O的直径,即BC=1m,
∵AB=AC,
∴∠ABC=∠ACB=45°,
∴∠AOC=90°,
∴OA=OC=BC=0.5m,
由勾股定理得AC===(m),
∴==π(m),S扇形ABC==m2
∴被剪掉的部分的面积为π×-
=m2.
设圆锥的底面圆的半径为rm,则2πr=,
∴r=m.
答:被剪掉的部分的面积为m2,圆锥的底面圆的半径是m.
20.
【解析】解:把代入
得:
令
∴B
令得
∴
∴
∴
过点C作CD⊥OB,连接OC,
由垂径定理可知:OD=1,∴sin∠CBD=
∴∠CBD=30°
∵BC=OC
∴∠BOC=300
,∴∠BCO=120°
∴S扇=
∵S△OBC=
∴S阴=
21.(1)图(1)中阴影部分的面积为4平方厘米;(2)阴影部分面积为平方厘米.
【解析】解:(1)由图可知,图(1)中右边正方形中的阴影部分的面积等于左边正方形中的空白部分的面积,
∴S阴影=2×2=4(平方厘米);
(2)如图,
S阴影=S梯形ABCG+S扇形GCE-S△ABE==25π(平方厘米).
22.(1)它的侧面展开图的圆心角为90°;(2)BB′=8.
【解析】解:(1)设它的侧面展开图的圆心角为n°,
根据题意得2πr=,
而l=2r,
所以2πr=,解得n=90,
所以它的侧面展开图的圆心角为90°;
(2)连接BB′,如图,
此时BB′为从B点出发沿圆锥侧面绕一圈回到B点的最短路径,
∵r=4,
∴l=2r=8,
∵∠BAB′=90°,
∴△ABB′为等腰直角三角形,
∴BB′=AB=8.
23.(1)如图所示,见解析;(2).
【解析】(1)如图所示:△A1B1C1,即为所求;
(2)如图,将△ABC绕点C顺时针方向旋转90°后,AC边扫过的部分的图形为扇形CA
A',根据勾股定理,CA,∴.
答案第1页,共2页
28.5弧长和扇形面积的计算-同步练习
时间:60分钟
一、单选题
1.已知某扇形的半径为6,圆心角的度数为,则扇形的弧长为(
)
A.
B.
C.
D.
2.一个滑轮起重装置如图所示,滑轮的半径是15cm,当重物上升15cn时,滑轮的一条半径OA绕轴心O按顺时针方向旋转的角度约为(
)(π取3.14,结果精确到1 )
A.115
B.60
C.57
D.29
3.如图,在中,,
,.将绕直角顶点逆时针旋转得
,则点转过的路径长为(
)
A.
B.
C.
D.
4.60°的圆心角所对的弧长是3πcm,则此弧所在圆的半径是(
)
A.6cm
B.7cm
C.8cm
D.9cm
5.一张圆心角为的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是(
)
A.
B.
C.
D.
6.如图,在中,,将△AOC绕点O顺时针旋转后得到,则AC边在旋转过程中所扫过的图形的面积为(
).
A.
B.
C.
D.
7.如图,在Rt中,∠BCA=90°
两分圆别以为半径画圆,则阴影部分的面积为(
)
A.
B.
C.
D.
8.如图,在中,,,以的中点为圆心,作圆心角为的扇形,点恰在上,设,当由小到大变化时,图中阴影部分的面积为(
)
A.
B.
C.
D.随的变化而变化
二、填空题
9.已知60°的圆心角所对的弧长为3cm,它所在的圆的周长是_________cm.
10.扇形的弧长和半径都是2,则其面积为________.
11.如图,若长为周长的,则_________.
12.半径为的圆中,的圆心角所对的弧长为__________;弧长为的圆心角约为________.
13.如图,扇形中,.若将此扇形绕点B顺时针旋转,得一新扇形,其中A点在上,则点O的运动路径长为_______.(结果保留)
14.如图,已知扇形AOB的半径为2,圆心角为,连接AB,则图中阴影部分的面积是________.
15.如图,在平行四边形ABCD中,AB<AD,∠A=150°,CD=4,以CD为直径的⊙O交AD于点E,则图中阴影部分的面积为_____.
16.如图,一根长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊(羊只能在草地上活动),那么小羊在草地上的最大活动区域面积是__________平方米.
三、解答题
17.上海外滩海关大钟时针长约为6米,从上午9时到当天下午6时,时针的针尖走过的路程是多少米?(取π=3.14)
18.如图,草坪上的自动喷水装置能旋转,它的喷灌区域是一个扇形,这个扇形的半径是.求它能喷灌的草坪的面积.
19.如图,从一块直径是的圆形铁皮上剪出一个圆心角为的扇形,求被剪掉的部分的面积;如果将剪下来的扇形围成一个圆锥,圆锥的底面圆的半径是多少?
20.如图,直线经过点M(1,)和点N(,3),A、B是此直线与坐标轴的交点.以AB为直径作⊙C,求此圆与y轴围成的阴影部分面积.
21.(1)求图(1)中阴影部分的面积(单位:厘米);
(2)如图(2)所示,已知大正方形的边长为10厘米,小正方形的边长为7厘米,求阴影部分面积.(结果保留)
22.如图,圆锥母线的长l等于底面半径r的4倍,
(1)求它的侧面展开图的圆心角.
(2)当圆锥的底面半径r=4cm时,求从B点出发沿圆锥侧面绕一圈回到B点的最短路径的长
23.如图,已知A(﹣2,3),B(﹣3,2),C(﹣1,1).
(1)画出△ABC关于原点O对称的△A1B1C1;
(2)若将△ABC绕点C顺时针方向旋转90°后,求AC边扫过的图形的面积.
试卷第1页,共3页
参考答案
1.C
【解析】∵扇形的半径为6,圆心角的度数为,
∴.
故选C.
2.C
【解析】设OA旋转的角度为n,由于重物上升15
cm,
则点A顺时针旋转的弧长为15
cm,
由弧长公式l=,
可求n=≈57度.
故选C.
3.B
【解析】解:在中,,,
,
,
绕直角顶点逆时针旋转得△,
,
弧的长.
故选:B.
4.D
【解析】∵l,∴r=9(cm).
故选D.
5.A
【解析】解:如图1,连接,
四边形是正方形,
,,
,
,
由勾股定理得:,
扇形的面积是;
如图2,连接、,
四边形是的内接四边形,四边形是正方形,
,,
,
,
,
的面积是,
扇形和圆形纸板的面积比是.
故选:A.
6.B
【解析】解:
∴阴影部分的面积=扇形OAB的面积﹣扇形OCD的面积
故选B.
7.A
【解析】设各个部分的面积为:S1、S2、S3、S4、S5,如图所示,
∵两个半圆的面积和是:S1+S5+S4+S2+S3+S4,△ABC的面积是S3+S4+S5,阴影部分
面积是:S1+S2+S4,
∴图中阴影部分的面积为两个半圆的面积减去三角形的面积.
即阴影部分的面积=π×4+π×1-4×2÷2=π-4.
故选A.
8.C
【解析】如图,连接,作于点,于点,
∵,,∴,
,,∴,
∴四边形是正方形,
∴,∴,
∵,∴,
∴,
在和中,
,
∴,
∴四边形的面积正方形的面积,
∵正方形的面积,
∴四边形的面积,
∵扇形的面积,
∴阴影部分的面积扇形的面积四边形的面积,恒为定值.
故选:C.
9.18
【解析】.
故答案为:18.
10.2
【解析】解:∵扇形的弧长和半径都是2,
∴.
故答案为:2.
11.
【解析】解:设∠AOB=x,圆的半径为r,
∴,圆的周长,
∵弧AB的长是圆周长的,
∴,
∴,
故答案为:.
12.
【解析】,
,
,,
故答案为:,
13.4π.
【解析】解:根据题意,知OA=OB.
又∠AOB=36°,
∴∠OBA=72°.
∴点O旋转至O′点所经过的轨迹长度==4πcm.
故答案是:4π.
14.π-2.
【解析】解:S阴影部分=S扇形OAB-S△OAB
= ×2×2
=π-2
故答案为π-2.
15.
【解析】如图,连接OE,作OF⊥DE于点F,
∵四边形ABCD是平行四边形,且∠A=150°,
∴∠D=30°,
则∠COE=2∠D=60°,
∵CD=4,
∴CO=DO=2,
∴OF=OD=1,DF=ODcos∠ODF=2×=,
∴DE=2DF=2,
∴图中阴影部分的面积为+×2×1=,
故答案为.
16..
【解析】解:如图.小羊的活动范围是:(平方米)
故答案为.
17.28.26m.
【解析】钟时针长为半径,从上午9时到当天下午6时指针走过270度.
所以时针的针尖走过的路程是28.26m.
18.它能喷灌的草坪的面积为m2.
【解析】解:由题意可知喷灌的草坪是一个圆心角为220°,半径为20m的扇形,
∴其面积是S==(m2).
答:它能喷灌的草坪的面积为(m2).
19.被剪掉的部分的面积为m2,圆锥的底面圆的半径是m.
【解析】解:连接AO,BC,
∵∠BAC=90°,
∴BC是⊙O的直径,即BC=1m,
∵AB=AC,
∴∠ABC=∠ACB=45°,
∴∠AOC=90°,
∴OA=OC=BC=0.5m,
由勾股定理得AC===(m),
∴==π(m),S扇形ABC==m2
∴被剪掉的部分的面积为π×-
=m2.
设圆锥的底面圆的半径为rm,则2πr=,
∴r=m.
答:被剪掉的部分的面积为m2,圆锥的底面圆的半径是m.
20.
【解析】解:把代入
得:
令
∴B
令得
∴
∴
∴
过点C作CD⊥OB,连接OC,
由垂径定理可知:OD=1,∴sin∠CBD=
∴∠CBD=30°
∵BC=OC
∴∠BOC=300
,∴∠BCO=120°
∴S扇=
∵S△OBC=
∴S阴=
21.(1)图(1)中阴影部分的面积为4平方厘米;(2)阴影部分面积为平方厘米.
【解析】解:(1)由图可知,图(1)中右边正方形中的阴影部分的面积等于左边正方形中的空白部分的面积,
∴S阴影=2×2=4(平方厘米);
(2)如图,
S阴影=S梯形ABCG+S扇形GCE-S△ABE==25π(平方厘米).
22.(1)它的侧面展开图的圆心角为90°;(2)BB′=8.
【解析】解:(1)设它的侧面展开图的圆心角为n°,
根据题意得2πr=,
而l=2r,
所以2πr=,解得n=90,
所以它的侧面展开图的圆心角为90°;
(2)连接BB′,如图,
此时BB′为从B点出发沿圆锥侧面绕一圈回到B点的最短路径,
∵r=4,
∴l=2r=8,
∵∠BAB′=90°,
∴△ABB′为等腰直角三角形,
∴BB′=AB=8.
23.(1)如图所示,见解析;(2).
【解析】(1)如图所示:△A1B1C1,即为所求;
(2)如图,将△ABC绕点C顺时针方向旋转90°后,AC边扫过的部分的图形为扇形CA
A',根据勾股定理,CA,∴.
答案第1页,共2页
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
