《2.5三角函数的应用》解答题专题训练 2021-2022学年鲁教版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 《2.5三角函数的应用》解答题专题训练 2021-2022学年鲁教版九年级数学上册(Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 479.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 00:00:00 | ||
图片预览

文档简介
2021-2022学年鲁教版九年级数学上册《2.5三角函数的应用》解答题专题训练(附答案)
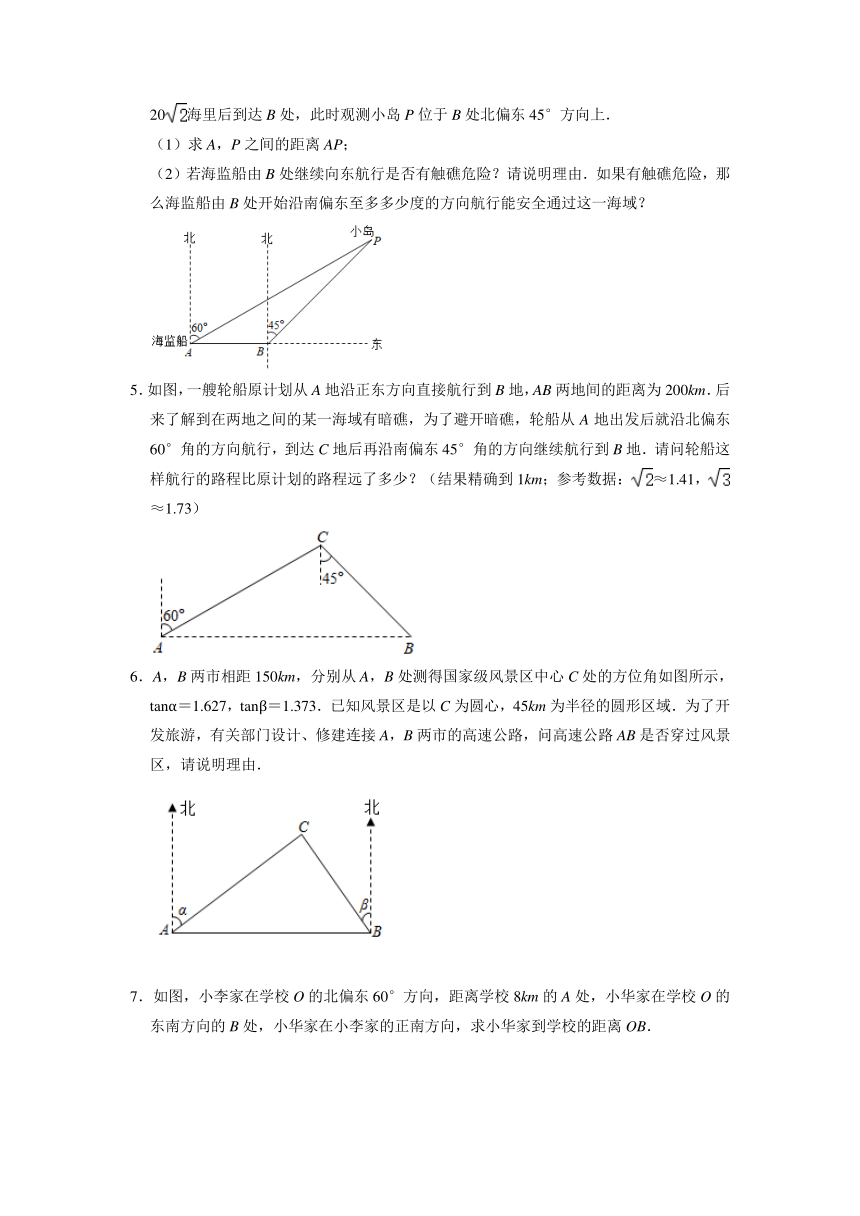
1.由我国完全自主设计、自主建造的某大型拖船近日完成海上测试.如图,拖船由西向东航行,到达A处时,测得小岛B位于它的北偏东30°方向,且与拖船相距80海里.继续航行一段时间后到达C处,测得小岛B位于它的西北方向.求此时拖船与小岛的距离BC的长(结果保留根号).
2.如图,一艘船由A港沿北偏东60°方向航行30海里至B港,然后再沿北偏西45°方向航行至C港,C港在A港北偏东15°方向,求A,C两港之间的距离(结果保留根号).
3.某景区A、B两个景点位于湖泊两侧,游客从景点A到景点B必须经过C处才能到达.观测得景点B在景点A的北偏东30°,从景点A出发向正北方向步行600米到达C处,测得景点B在C的北偏东75°方向.
(1)求景点B和C处之间的距离;(结果保留根号)
(2)当地政府为了便捷游客游览,打算修建一条从景点A到景点B的笔直的跨湖大桥.大桥修建后,从景点A到景点B比原来少走多少米?(结果保留整数.参考数据:≈1.414,≈1.732)
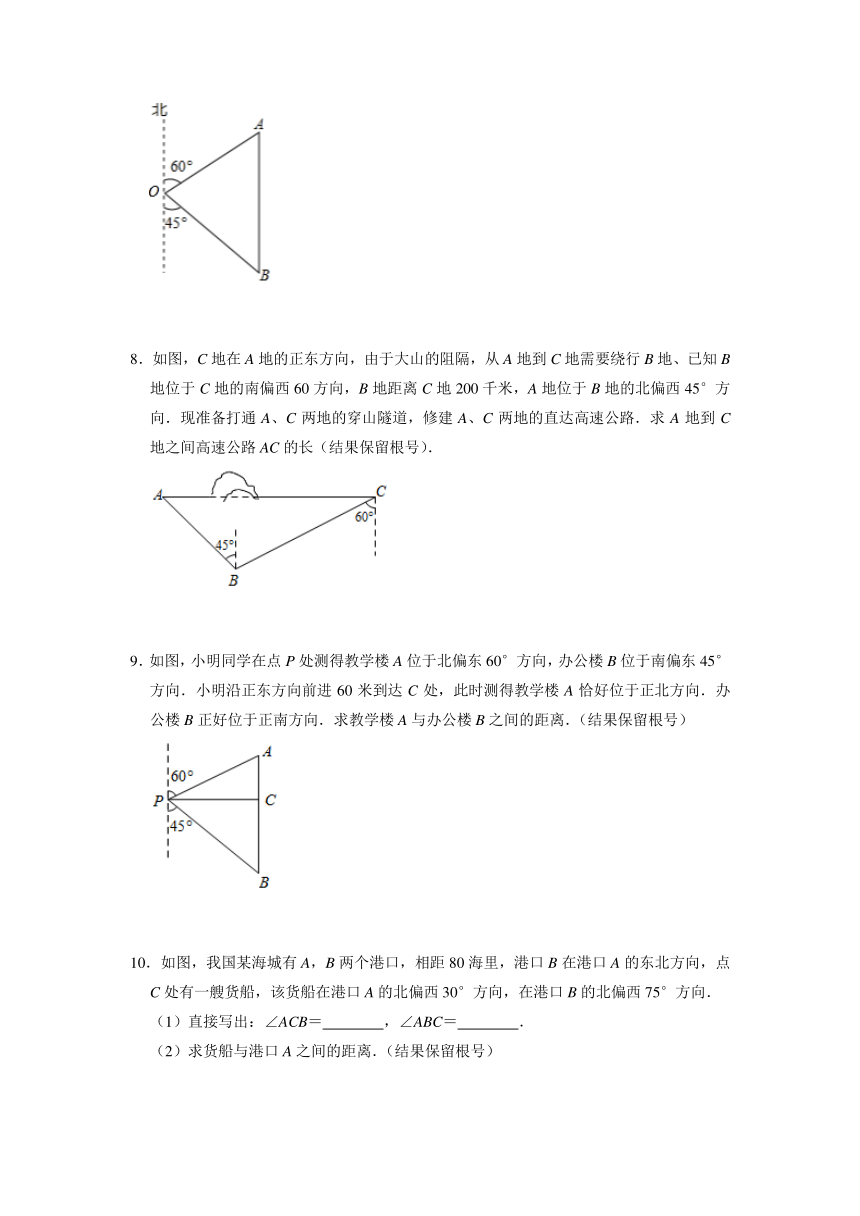
4.某海域有一小岛P,在以P为圆心,半径r为10(3+)海里的圆形海域内有暗礁.一海监船自西向东航行,它在A处测得小岛P位于北偏东60°的方向上,当海监船行驶20海里后到达B处,此时观测小岛P位于B处北偏东45°方向上.
(1)求A,P之间的距离AP;
(2)若海监船由B处继续向东航行是否有触礁危险?请说明理由.如果有触礁危险,那么海监船由B处开始沿南偏东至多多少度的方向航行能安全通过这一海域?
5.如图,一艘轮船原计划从A地沿正东方向直接航行到B地,AB两地间的距离为200km.后来了解到在两地之间的某一海域有暗礁,为了避开暗礁,轮船从A地出发后就沿北偏东60°角的方向航行,到达C地后再沿南偏东45°角的方向继续航行到B地.请问轮船这样航行的路程比原计划的路程远了多少?(结果精确到1km;参考数据:≈1.41,≈1.73)
6.A,B两市相距150km,分别从A,B处测得国家级风景区中心C处的方位角如图所示,tanα=1.627,tanβ=1.373.已知风景区是以C为圆心,45km为半径的圆形区域.为了开发旅游,有关部门设计、修建连接A,B两市的高速公路,问高速公路AB是否穿过风景区,请说明理由.
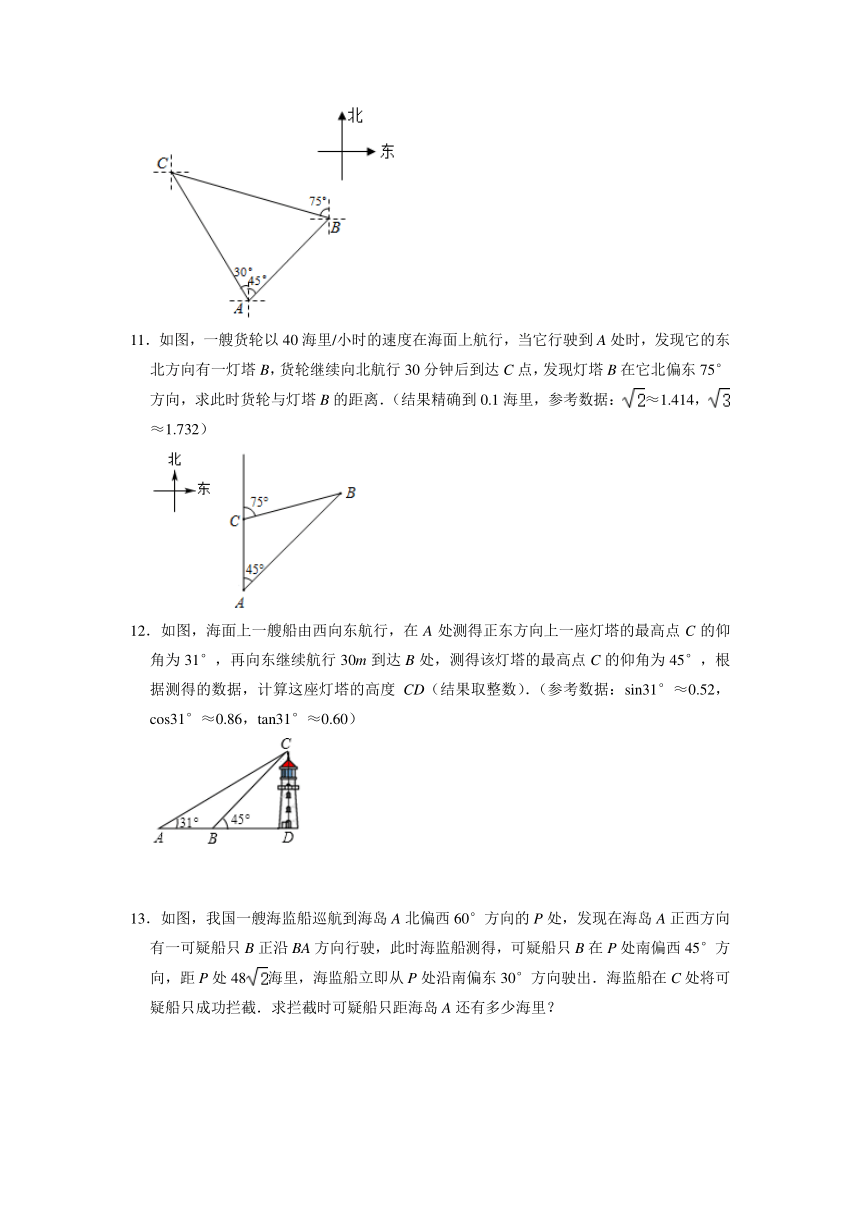
7.如图,小李家在学校O的北偏东60°方向,距离学校8km的A处,小华家在学校O的东南方向的B处,小华家在小李家的正南方向,求小华家到学校的距离OB.
8.如图,C地在A地的正东方向,由于大山的阻隔,从A地到C地需要绕行B地、已知B地位于C地的南偏西60方向,B地距离C地200千米,A地位于B地的北偏西45°方向.现准备打通A、C两地的穿山隧道,修建A、C两地的直达高速公路.求A地到C地之间高速公路AC的长(结果保留根号).
9.如图,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向.办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离.(结果保留根号)
10.如图,我国某海城有A,B两个港口,相距80海里,港口B在港口A的东北方向,点C处有一艘货船,该货船在港口A的北偏西30°方向,在港口B的北偏西75°方向.
(1)直接写出:∠ACB=
,∠ABC=
.
(2)求货船与港口A之间的距离.(结果保留根号)
11.如图,一艘货轮以40海里/小时的速度在海面上航行,当它行驶到A处时,发现它的东北方向有一灯塔B,货轮继续向北航行30分钟后到达C点,发现灯塔B在它北偏东75°方向,求此时货轮与灯塔B的距离.(结果精确到0.1海里,参考数据:≈1.414,≈1.732)
12.如图,海面上一艘船由西向东航行,在A处测得正东方向上一座灯塔的最高点C的仰角为31°,再向东继续航行30m到达B处,测得该灯塔的最高点C的仰角为45°,根据测得的数据,计算这座灯塔的高度CD(结果取整数).(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
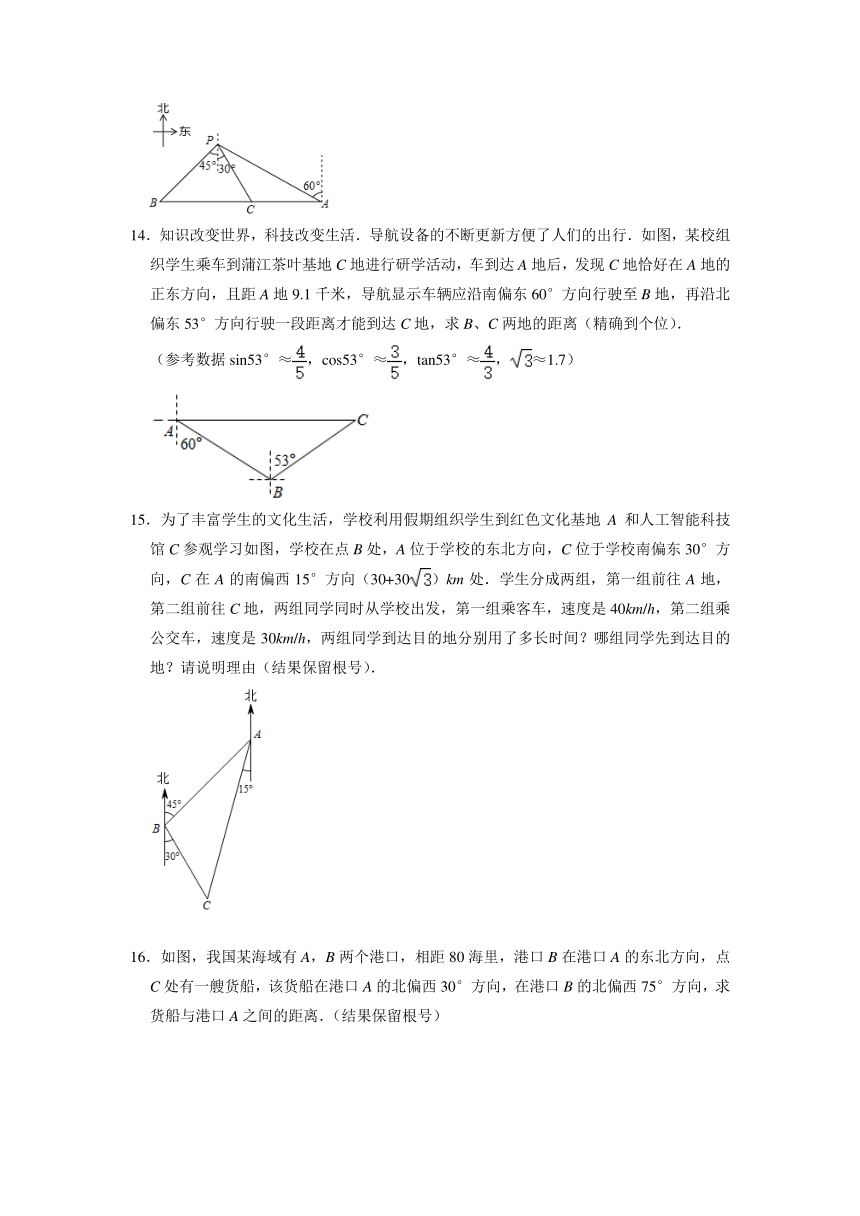
13.如图,我国一艘海监船巡航到海岛A北偏西60°方向的P处,发现在海岛A正西方向有一可疑船只B正沿BA方向行驶,此时海监船测得,可疑船只B在P处南偏西45°方向,距P处48海里,海监船立即从P处沿南偏东30°方向驶出.海监船在C处将可疑船只成功拦截.求拦截时可疑船只距海岛A还有多少海里?
14.知识改变世界,科技改变生活.导航设备的不断更新方便了人们的出行.如图,某校组织学生乘车到蒲江茶叶基地C地进行研学活动,车到达A地后,发现C地恰好在A地的正东方向,且距A地9.1千米,导航显示车辆应沿南偏东60°方向行驶至B地,再沿北偏东53°方向行驶一段距离才能到达C地,求B、C两地的距离(精确到个位).
(参考数据sin53°≈,cos53°≈,tan53°≈,≈1.7)
15.为了丰富学生的文化生活,学校利用假期组织学生到红色文化基地A和人工智能科技馆C参观学习如图,学校在点B处,A位于学校的东北方向,C位于学校南偏东30°方向,C在A的南偏西15°方向(30+30)km处.学生分成两组,第一组前往A地,第二组前往C地,两组同学同时从学校出发,第一组乘客车,速度是40km/h,第二组乘公交车,速度是30km/h,两组同学到达目的地分别用了多长时间?哪组同学先到达目的地?请说明理由(结果保留根号).
16.如图,我国某海域有A,B两个港口,相距80海里,港口B在港口A的东北方向,点C处有一艘货船,该货船在港口A的北偏西30°方向,在港口B的北偏西75°方向,求货船与港口A之间的距离.(结果保留根号)
17.如图,一艘小船以11nmile/h的速度向正北方向航行,在A处测得灯塔C在北偏东37°方向,航行2h后到达B处,测得灯塔C在南偏东42°方向,求B处距离灯塔C的距离BC(结果保留1位小数).参考数据:tan37°≈0.75,sin42°≈0.67,tan42°≈0.90.
18.时代中学组织学生进行红色研学活动.学生到达爱国主义教育基地后,先从基地门口A处向正南方向走300米到达革命纪念碑B处,再从B处向正东方向走到党史纪念馆C处,然后从C处向北偏西37°方向走200米到达人民英雄雕塑D处,最后从D处回到A处.已知人民英雄雕塑在基地门口的南偏东65°方向,求革命纪念碑与党史纪念馆之间的距离(精确到1米).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
19.如图,一艘货船在灯塔C的正南方向,距离灯塔257海里的A处遇险,发出求救信号.一艘救生船位于灯塔C的南偏东40°方向上,同时位于A处的北偏东60°方向上的B处,救生船接到求救信号后,立即前往救援.求AB的长.(结果取整数)参考数据:tan40°≈0.84,取1.73.
20.如图,港口B位于港口A的南偏东30°方向,灯塔C恰好在AB的中点处,一艘海轮从港口A出发,沿正南方向航行35km到达E处,测得灯塔C在北偏东45°方向上.
(1)E到灯塔C的距离为多少?
(2)海轮还要行驶多远才能到达位于港口B正西方向的D处?(结果保留根号)
参考答案
1.解:过点B作BD⊥AC于点D,
由题意得:∠BAD=90°﹣30°=60°,∠BCD=90°﹣45°=45°,AB=80海里,
在Rt△ADB中,∠BAD=60°,
∵sin∠BAD==,
∴BD=AB=40(海里),
在Rt△BCD中,∠BCD=45°,
∴△BCD是等腰直角三角形,
∴BD=CD=40(海里),
∴BC=BD=40(海里),
答:此时拖船与小岛的距离BC的长为40海里.
2.解:根据题意得:∠CAB=60°﹣15°=45°,∠ACB=45°+15°=60°,AB=30海里,
过B作BE⊥AC于E,
∴∠AEB=∠CEB=90°,
在Rt△ABE中,∵∠ABE=45°,
∴△ABE是等腰直角三角形,
∴AE=BE=AB=15(海里),
在Rt△CBE中,∵∠ACB=60°,
∴∠CBE=30°,
∴CE=BE=5(海里),
∴AC=AE+CE=(15+5)海里,
即A,C两港之间的距离为(15+5)海里.
3.解:(1)过点C作CD⊥AB于点D,
由题意得,∠A=30°,∠BCE=75°,AC=600m,
在Rt△ACD中,∠A=30°,AC=600,
∴CD=AC=300(m),
AD=AC=300(m),
∵∠BCE=75°=∠A+∠B,
∴∠B=75°﹣∠A=45°,
∴CD=BD=300(m),
BC=CD=300(m),
答:景点B和C处之间的距离为300m;
(2)由题意得.
AC+BC=(600+300)m,
AB=AD+BD=(300+300)m,
AC+BC﹣AB=(600+300)﹣(300+300)
≈204.6
≈205(m),
答:大桥修建后,从景点A到景点B比原来少走约205m.
4.解:(1)过点P作PC⊥AB,交AB的延长线于点C,
由题意得,∠PAC=30°,∠PBC=45°,AB=20,
设PC=x,则BC=x,
在Rt△PAC中,
∵tan30°===,
∴x=10+10,
∴PA=2x=20+20,
答:A,P之间的距离AP为(20+20)海里;
(2)因为PC﹣10(3+)=10+10﹣30﹣10=10(+1)(﹣)<0,
所以有触礁的危险;
设海监船无触礁危险的新航线为射线BD,作PE⊥BD,垂足为E,
当P到BD的距离PE=10(3+)海里时,
有sin∠PBE===,
∴∠PBD=60°,
∴∠CBD=60°﹣45°=15°,
90°﹣15°=75°
即海监船由B处开始沿南偏东至多75°的方向航行能安全通过这一海域.
5.解:过点C作CD⊥AB于点D,如图所示:
则∠CAD=90°﹣60°=30°,∠CBD=45°,AD==CD,BD==CD,
∵AD+BD=AB,
∴(+1)CD=200km,
∴CD=100(﹣1)km,
在Rt△ACD中,AC=200(﹣1)km,
在Rt△BCD中,BC=100(﹣1),
AC+BC=200(﹣1)+100(﹣1)≈249(km),
249﹣200=49(km),
答:飞机的飞行路程比原来的路程远了约49km.
6.解:AB不穿过风景区.理由如下:
如图,过C作CD⊥AB于点D,
根据题意得,∠ACD=α,∠BCD=β,
在Rt△ACD中,tanα=,即AD=CD tanα,
在Rt△BCD中,tanβ=,即BD=CD tanβ,
∵AD+DB=AB,
∴CD tanα+CD tanβ=AB,
∴CD====50(km).
∵CD=50>45,
∴高速公路AB不穿过风景区.
7.解:过点O作OC⊥AB,垂足为C,则∠AOC=90°﹣60°=30°,
∠BOC=90°﹣45°=45°,
在Rt△AOC中,
OC=OA cos30°=8×=4(km),
在Rt△BOC中,
OB===4(km),
答:小华家到学校的距离OB为4km.
8.解:如图,过点B作BD⊥AC于点D,
根据题意,得∠CBD=60°,CB=200,∠ABD=45°,
在Rt△CBD中,BD=CB cos60°=200×=100(千米),CD=CB sin60°=200×=100(千米),
在Rt△ABD中,AD=BD tan45°=100(千米),
∴(千米),
答:A地到C地之间高速公路AC长千米.
9.解:由题意可知:∠ACP=∠BCP=90°,∠APC=90°﹣60°=30°,∠BPC=45°.
在Rt△BPC中,∠BCP=90°,∠B=∠BPC=45°,
∴BC=PC=60米,
在Rt△ACP中,∠ACP=90°,∠APC=30°,
∵tan30°=,
∴AC=PC tan30°=tan30°×60=60×=20(米).
∴AB=AC+BC=(60+20)米,
答:教学楼A与办公楼B之间的距离是(60+20)米.
10.解:(1)∠ACB=90°﹣30°﹣(90°﹣75°)=45°,∠ABC=180°﹣75°﹣45°=60°,
故答案为:45°,60°;
(2)过点A作AD⊥BC于D,如图所示:
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD中,∵∠ABD=60°
∴∠DAB=90°﹣60°=30°,(海里),
∵∠CAB=30°+45°=75°,
∴∠DAC=∠CAB﹣∠DAB=75°﹣30°=45°,
∵∠ACB=45°
∴∠DAC=∠ACB=45°,
∴CD=AD=(海里),
∴△ADC是等腰直角三角形,
∴(海里),
答:货船与港口A之间的距离是海里.
11.解:如图所示:过点C作CD⊥AB于点D,
∵货轮以40海里/小时的速度在海面上航行,向北航行30分钟后到达C点
∴AC=40×=20海里,
∵∠A=45°,∠1=75°,
∴∠ACD=45°,∠DCB=60°,
则∠B=30°,
则DC=ACsin45°=20×=10海里,
故BC=2CD=20≈28.3海里.
答:此时货轮与灯塔B的距离约为28.3海里.
12.解:在Rt△CAD中,,
则,
在Rt△CBD中,∠CBD=45°,
∴BD=CD,
∵AD=AB+BD,
∴,
解得,CD=45(m).
答:这座灯塔的高度CD约为45m.
13.解:如图所示,过点P作PD⊥AB于点D,
由题意可知:
∠BPD=45°,∠CPD=30°,∠PAC=30°,PB=48(海里),
在Rt△BPD中,∵∠BPD=45°,
∴PD=BD=PBsin∠BPD=48×=48(海里),
在Rt△CPD中,∠CPD=30°,
∵cos∠CPD=,
∴PC===32(海里),
∵∠PCD=60°,∠PAC=30°,
∴∠PAC=∠APC=30°,
∴AC=PC=32(海里),
答:被拦截时,可疑船只距海岛A还有32海里.
14.解:如图,过点B作BD⊥AC于点D,
由题意可知:∠DBA=60°,
在Rt△ABD中,
∵tan∠DBA=,
∴AD=BD,
在Rt△CBD中,∠DBC=53°,
∵tan∠DBC=,
∴CD=BD,
∵AD+CD=AC=9.1(千米),
∴BD+BD=9.1,
解得BD=3(千米),
在Rt△CBD中,∠DBC=53°,
∵cos53°=,
∴BC===5(千米).
答:B、C两地的距离为5千米.
15.解:作BD⊥AC于D.
依题意得,
∠BAE=45°,∠ABC=105°,∠CAE=15°,
∴∠BAC=30°,
∴∠ACB=45°.
在Rt△BCD中,∠BDC=90°,∠ACB=45°,
∴∠CBD=45°,
∴∠CBD=∠DCB,
∴BD=CD,
设BD=x,则CD=x,
在Rt△ABD中,∠BAC=30°,
∴AB=2BD=2x,tan30°=,
∴,
∴AD=x,
在Rt△BDC中,∠BDC=90°,∠DCB=45°,
∴sin∠DCB=,
∴BC=x,
∵CD+AD=30+30,
∴x+,
∴x=30,
∴AB=2x=60,BC=,
第一组用时:60÷40=1.5(h);第二组用时:30(h),
∵<1.5,
∴第二组先到达目的地,
答:第一组用时1.5小时,第二组用时小时,第二组先到达目的地.
16.解:过点A作AD⊥BC于D,如图所示:
由题意得:∠ABC=180°﹣75°﹣45°=60°,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD中,∠DAB=90°﹣60°=30°,AD=AB sin∠ABD=80×sin60°=80×=40(海里),
∵∠CAB=30°+45°=75°,
∴∠DAC=∠CAB﹣∠DAB=75°﹣30°=45°,
∴△ADC是等腰直角三角形,
∴AC=AD=×40=40(海里).
答:货船与港口A之间的距离是40海里.
17.解:过C作CH⊥AB于H,
根据题意,∠HBC=42°,∠HAC=37°,AB=22(nmile),
∵在Rt△CBH中,tan∠HBC=,
∴BH=.
∵在Rt△ACH中,tan∠HAC=,
∴AH=,
∵AB=AH+BH,
∴=AB.
∴CH=≈=9.00(nmile).
∵在Rt△CBH中,sin∠HBC=,
∴BC=≈13.4(nmile).
答:B处距离灯塔C的距离BC约为13.4nmile.
18.解:过D作DE⊥AB于E,DF⊥BC于F,如图所示:
由题意得:∠CDF=37°,CD=200米,
在Rt△CDF中,sin∠CDF==sin37°≈0.60,cos∠CDF==cos37°≈0.80,
∴CF≈200×0.60=120(米),DF≈200×0.80=160(米),
∵AB⊥BC,DF⊥BC,DE⊥AB,
∴∠B=∠DFB=∠DEB=90°,
∴四边形BFDE是矩形,
∴BF=DE,BE=DF=160米,
∴AE=AB﹣BE=300﹣160=140(米),
在Rt△ADE中,tan∠DAE==tan65°≈2.14,
∴DE≈AE×2.14=140×2.14=299.60(米),
∴BF=DE≈299.60(米),
∴BC=BF+CF=299.60+120≈420(米),
答:革命纪念碑与党史纪念馆之间的距离约为420米.
19.解:如图,过点B作BH⊥AC,垂足为H,
由题意得,∠BAC=60°,∠BCA=40°,AC=257海里,
在Rt△ABH中,
∵tan∠BAH=,cos∠BAH=,
∴BH=AH tan60°=AH,AB==2AH,
在Rt△BCH中,
∵tan∠BCH=,
∴CH==(海里),
又∵CA=CH+AH,
∴257=+AH,
所以AH=(海里),
∴AB=≈=168(海里),
答:AB的长约为168海里.
20.解:(1)如图,过点C作CH⊥AD,垂足为H.
由题意可知∠A=30°,∠AEC=45°,AE=35且AC=BC,
在Rt△CEH中,
∵∠CEH=45°,
∴CH=EH,
在Rt△ACH中,
∵∠A=30°,
∴AH=CH,
设AH=xkm,则EH=xkm,AH=xkm,
∵AE=35=AH+HE,
∴x+x=35,
解得x=,
即CH=EH=,
∴EC=CH=×=(km),
(2)在Rt△ACH中,
∵∠A=30°,
∴AC=2HC=(35﹣35)km,
在Rt△ABD中,
∵∠A=30°,
∴BD=AB=AC=BC=(35﹣35)km,
AD=BD=(35﹣35)=(105﹣35)km,
∴ED=AD﹣AE=(105﹣35)﹣35=(70﹣35)km,
答:海轮还要行驶(70﹣35)km才能到达位于港口B正西方向的D处.
1.由我国完全自主设计、自主建造的某大型拖船近日完成海上测试.如图,拖船由西向东航行,到达A处时,测得小岛B位于它的北偏东30°方向,且与拖船相距80海里.继续航行一段时间后到达C处,测得小岛B位于它的西北方向.求此时拖船与小岛的距离BC的长(结果保留根号).
2.如图,一艘船由A港沿北偏东60°方向航行30海里至B港,然后再沿北偏西45°方向航行至C港,C港在A港北偏东15°方向,求A,C两港之间的距离(结果保留根号).
3.某景区A、B两个景点位于湖泊两侧,游客从景点A到景点B必须经过C处才能到达.观测得景点B在景点A的北偏东30°,从景点A出发向正北方向步行600米到达C处,测得景点B在C的北偏东75°方向.
(1)求景点B和C处之间的距离;(结果保留根号)
(2)当地政府为了便捷游客游览,打算修建一条从景点A到景点B的笔直的跨湖大桥.大桥修建后,从景点A到景点B比原来少走多少米?(结果保留整数.参考数据:≈1.414,≈1.732)
4.某海域有一小岛P,在以P为圆心,半径r为10(3+)海里的圆形海域内有暗礁.一海监船自西向东航行,它在A处测得小岛P位于北偏东60°的方向上,当海监船行驶20海里后到达B处,此时观测小岛P位于B处北偏东45°方向上.
(1)求A,P之间的距离AP;
(2)若海监船由B处继续向东航行是否有触礁危险?请说明理由.如果有触礁危险,那么海监船由B处开始沿南偏东至多多少度的方向航行能安全通过这一海域?
5.如图,一艘轮船原计划从A地沿正东方向直接航行到B地,AB两地间的距离为200km.后来了解到在两地之间的某一海域有暗礁,为了避开暗礁,轮船从A地出发后就沿北偏东60°角的方向航行,到达C地后再沿南偏东45°角的方向继续航行到B地.请问轮船这样航行的路程比原计划的路程远了多少?(结果精确到1km;参考数据:≈1.41,≈1.73)
6.A,B两市相距150km,分别从A,B处测得国家级风景区中心C处的方位角如图所示,tanα=1.627,tanβ=1.373.已知风景区是以C为圆心,45km为半径的圆形区域.为了开发旅游,有关部门设计、修建连接A,B两市的高速公路,问高速公路AB是否穿过风景区,请说明理由.
7.如图,小李家在学校O的北偏东60°方向,距离学校8km的A处,小华家在学校O的东南方向的B处,小华家在小李家的正南方向,求小华家到学校的距离OB.
8.如图,C地在A地的正东方向,由于大山的阻隔,从A地到C地需要绕行B地、已知B地位于C地的南偏西60方向,B地距离C地200千米,A地位于B地的北偏西45°方向.现准备打通A、C两地的穿山隧道,修建A、C两地的直达高速公路.求A地到C地之间高速公路AC的长(结果保留根号).
9.如图,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向.办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离.(结果保留根号)
10.如图,我国某海城有A,B两个港口,相距80海里,港口B在港口A的东北方向,点C处有一艘货船,该货船在港口A的北偏西30°方向,在港口B的北偏西75°方向.
(1)直接写出:∠ACB=
,∠ABC=
.
(2)求货船与港口A之间的距离.(结果保留根号)
11.如图,一艘货轮以40海里/小时的速度在海面上航行,当它行驶到A处时,发现它的东北方向有一灯塔B,货轮继续向北航行30分钟后到达C点,发现灯塔B在它北偏东75°方向,求此时货轮与灯塔B的距离.(结果精确到0.1海里,参考数据:≈1.414,≈1.732)
12.如图,海面上一艘船由西向东航行,在A处测得正东方向上一座灯塔的最高点C的仰角为31°,再向东继续航行30m到达B处,测得该灯塔的最高点C的仰角为45°,根据测得的数据,计算这座灯塔的高度CD(结果取整数).(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
13.如图,我国一艘海监船巡航到海岛A北偏西60°方向的P处,发现在海岛A正西方向有一可疑船只B正沿BA方向行驶,此时海监船测得,可疑船只B在P处南偏西45°方向,距P处48海里,海监船立即从P处沿南偏东30°方向驶出.海监船在C处将可疑船只成功拦截.求拦截时可疑船只距海岛A还有多少海里?
14.知识改变世界,科技改变生活.导航设备的不断更新方便了人们的出行.如图,某校组织学生乘车到蒲江茶叶基地C地进行研学活动,车到达A地后,发现C地恰好在A地的正东方向,且距A地9.1千米,导航显示车辆应沿南偏东60°方向行驶至B地,再沿北偏东53°方向行驶一段距离才能到达C地,求B、C两地的距离(精确到个位).
(参考数据sin53°≈,cos53°≈,tan53°≈,≈1.7)
15.为了丰富学生的文化生活,学校利用假期组织学生到红色文化基地A和人工智能科技馆C参观学习如图,学校在点B处,A位于学校的东北方向,C位于学校南偏东30°方向,C在A的南偏西15°方向(30+30)km处.学生分成两组,第一组前往A地,第二组前往C地,两组同学同时从学校出发,第一组乘客车,速度是40km/h,第二组乘公交车,速度是30km/h,两组同学到达目的地分别用了多长时间?哪组同学先到达目的地?请说明理由(结果保留根号).
16.如图,我国某海域有A,B两个港口,相距80海里,港口B在港口A的东北方向,点C处有一艘货船,该货船在港口A的北偏西30°方向,在港口B的北偏西75°方向,求货船与港口A之间的距离.(结果保留根号)
17.如图,一艘小船以11nmile/h的速度向正北方向航行,在A处测得灯塔C在北偏东37°方向,航行2h后到达B处,测得灯塔C在南偏东42°方向,求B处距离灯塔C的距离BC(结果保留1位小数).参考数据:tan37°≈0.75,sin42°≈0.67,tan42°≈0.90.
18.时代中学组织学生进行红色研学活动.学生到达爱国主义教育基地后,先从基地门口A处向正南方向走300米到达革命纪念碑B处,再从B处向正东方向走到党史纪念馆C处,然后从C处向北偏西37°方向走200米到达人民英雄雕塑D处,最后从D处回到A处.已知人民英雄雕塑在基地门口的南偏东65°方向,求革命纪念碑与党史纪念馆之间的距离(精确到1米).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
19.如图,一艘货船在灯塔C的正南方向,距离灯塔257海里的A处遇险,发出求救信号.一艘救生船位于灯塔C的南偏东40°方向上,同时位于A处的北偏东60°方向上的B处,救生船接到求救信号后,立即前往救援.求AB的长.(结果取整数)参考数据:tan40°≈0.84,取1.73.
20.如图,港口B位于港口A的南偏东30°方向,灯塔C恰好在AB的中点处,一艘海轮从港口A出发,沿正南方向航行35km到达E处,测得灯塔C在北偏东45°方向上.
(1)E到灯塔C的距离为多少?
(2)海轮还要行驶多远才能到达位于港口B正西方向的D处?(结果保留根号)
参考答案
1.解:过点B作BD⊥AC于点D,
由题意得:∠BAD=90°﹣30°=60°,∠BCD=90°﹣45°=45°,AB=80海里,
在Rt△ADB中,∠BAD=60°,
∵sin∠BAD==,
∴BD=AB=40(海里),
在Rt△BCD中,∠BCD=45°,
∴△BCD是等腰直角三角形,
∴BD=CD=40(海里),
∴BC=BD=40(海里),
答:此时拖船与小岛的距离BC的长为40海里.
2.解:根据题意得:∠CAB=60°﹣15°=45°,∠ACB=45°+15°=60°,AB=30海里,
过B作BE⊥AC于E,
∴∠AEB=∠CEB=90°,
在Rt△ABE中,∵∠ABE=45°,
∴△ABE是等腰直角三角形,
∴AE=BE=AB=15(海里),
在Rt△CBE中,∵∠ACB=60°,
∴∠CBE=30°,
∴CE=BE=5(海里),
∴AC=AE+CE=(15+5)海里,
即A,C两港之间的距离为(15+5)海里.
3.解:(1)过点C作CD⊥AB于点D,
由题意得,∠A=30°,∠BCE=75°,AC=600m,
在Rt△ACD中,∠A=30°,AC=600,
∴CD=AC=300(m),
AD=AC=300(m),
∵∠BCE=75°=∠A+∠B,
∴∠B=75°﹣∠A=45°,
∴CD=BD=300(m),
BC=CD=300(m),
答:景点B和C处之间的距离为300m;
(2)由题意得.
AC+BC=(600+300)m,
AB=AD+BD=(300+300)m,
AC+BC﹣AB=(600+300)﹣(300+300)
≈204.6
≈205(m),
答:大桥修建后,从景点A到景点B比原来少走约205m.
4.解:(1)过点P作PC⊥AB,交AB的延长线于点C,
由题意得,∠PAC=30°,∠PBC=45°,AB=20,
设PC=x,则BC=x,
在Rt△PAC中,
∵tan30°===,
∴x=10+10,
∴PA=2x=20+20,
答:A,P之间的距离AP为(20+20)海里;
(2)因为PC﹣10(3+)=10+10﹣30﹣10=10(+1)(﹣)<0,
所以有触礁的危险;
设海监船无触礁危险的新航线为射线BD,作PE⊥BD,垂足为E,
当P到BD的距离PE=10(3+)海里时,
有sin∠PBE===,
∴∠PBD=60°,
∴∠CBD=60°﹣45°=15°,
90°﹣15°=75°
即海监船由B处开始沿南偏东至多75°的方向航行能安全通过这一海域.
5.解:过点C作CD⊥AB于点D,如图所示:
则∠CAD=90°﹣60°=30°,∠CBD=45°,AD==CD,BD==CD,
∵AD+BD=AB,
∴(+1)CD=200km,
∴CD=100(﹣1)km,
在Rt△ACD中,AC=200(﹣1)km,
在Rt△BCD中,BC=100(﹣1),
AC+BC=200(﹣1)+100(﹣1)≈249(km),
249﹣200=49(km),
答:飞机的飞行路程比原来的路程远了约49km.
6.解:AB不穿过风景区.理由如下:
如图,过C作CD⊥AB于点D,
根据题意得,∠ACD=α,∠BCD=β,
在Rt△ACD中,tanα=,即AD=CD tanα,
在Rt△BCD中,tanβ=,即BD=CD tanβ,
∵AD+DB=AB,
∴CD tanα+CD tanβ=AB,
∴CD====50(km).
∵CD=50>45,
∴高速公路AB不穿过风景区.
7.解:过点O作OC⊥AB,垂足为C,则∠AOC=90°﹣60°=30°,
∠BOC=90°﹣45°=45°,
在Rt△AOC中,
OC=OA cos30°=8×=4(km),
在Rt△BOC中,
OB===4(km),
答:小华家到学校的距离OB为4km.
8.解:如图,过点B作BD⊥AC于点D,
根据题意,得∠CBD=60°,CB=200,∠ABD=45°,
在Rt△CBD中,BD=CB cos60°=200×=100(千米),CD=CB sin60°=200×=100(千米),
在Rt△ABD中,AD=BD tan45°=100(千米),
∴(千米),
答:A地到C地之间高速公路AC长千米.
9.解:由题意可知:∠ACP=∠BCP=90°,∠APC=90°﹣60°=30°,∠BPC=45°.
在Rt△BPC中,∠BCP=90°,∠B=∠BPC=45°,
∴BC=PC=60米,
在Rt△ACP中,∠ACP=90°,∠APC=30°,
∵tan30°=,
∴AC=PC tan30°=tan30°×60=60×=20(米).
∴AB=AC+BC=(60+20)米,
答:教学楼A与办公楼B之间的距离是(60+20)米.
10.解:(1)∠ACB=90°﹣30°﹣(90°﹣75°)=45°,∠ABC=180°﹣75°﹣45°=60°,
故答案为:45°,60°;
(2)过点A作AD⊥BC于D,如图所示:
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD中,∵∠ABD=60°
∴∠DAB=90°﹣60°=30°,(海里),
∵∠CAB=30°+45°=75°,
∴∠DAC=∠CAB﹣∠DAB=75°﹣30°=45°,
∵∠ACB=45°
∴∠DAC=∠ACB=45°,
∴CD=AD=(海里),
∴△ADC是等腰直角三角形,
∴(海里),
答:货船与港口A之间的距离是海里.
11.解:如图所示:过点C作CD⊥AB于点D,
∵货轮以40海里/小时的速度在海面上航行,向北航行30分钟后到达C点
∴AC=40×=20海里,
∵∠A=45°,∠1=75°,
∴∠ACD=45°,∠DCB=60°,
则∠B=30°,
则DC=ACsin45°=20×=10海里,
故BC=2CD=20≈28.3海里.
答:此时货轮与灯塔B的距离约为28.3海里.
12.解:在Rt△CAD中,,
则,
在Rt△CBD中,∠CBD=45°,
∴BD=CD,
∵AD=AB+BD,
∴,
解得,CD=45(m).
答:这座灯塔的高度CD约为45m.
13.解:如图所示,过点P作PD⊥AB于点D,
由题意可知:
∠BPD=45°,∠CPD=30°,∠PAC=30°,PB=48(海里),
在Rt△BPD中,∵∠BPD=45°,
∴PD=BD=PBsin∠BPD=48×=48(海里),
在Rt△CPD中,∠CPD=30°,
∵cos∠CPD=,
∴PC===32(海里),
∵∠PCD=60°,∠PAC=30°,
∴∠PAC=∠APC=30°,
∴AC=PC=32(海里),
答:被拦截时,可疑船只距海岛A还有32海里.
14.解:如图,过点B作BD⊥AC于点D,
由题意可知:∠DBA=60°,
在Rt△ABD中,
∵tan∠DBA=,
∴AD=BD,
在Rt△CBD中,∠DBC=53°,
∵tan∠DBC=,
∴CD=BD,
∵AD+CD=AC=9.1(千米),
∴BD+BD=9.1,
解得BD=3(千米),
在Rt△CBD中,∠DBC=53°,
∵cos53°=,
∴BC===5(千米).
答:B、C两地的距离为5千米.
15.解:作BD⊥AC于D.
依题意得,
∠BAE=45°,∠ABC=105°,∠CAE=15°,
∴∠BAC=30°,
∴∠ACB=45°.
在Rt△BCD中,∠BDC=90°,∠ACB=45°,
∴∠CBD=45°,
∴∠CBD=∠DCB,
∴BD=CD,
设BD=x,则CD=x,
在Rt△ABD中,∠BAC=30°,
∴AB=2BD=2x,tan30°=,
∴,
∴AD=x,
在Rt△BDC中,∠BDC=90°,∠DCB=45°,
∴sin∠DCB=,
∴BC=x,
∵CD+AD=30+30,
∴x+,
∴x=30,
∴AB=2x=60,BC=,
第一组用时:60÷40=1.5(h);第二组用时:30(h),
∵<1.5,
∴第二组先到达目的地,
答:第一组用时1.5小时,第二组用时小时,第二组先到达目的地.
16.解:过点A作AD⊥BC于D,如图所示:
由题意得:∠ABC=180°﹣75°﹣45°=60°,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD中,∠DAB=90°﹣60°=30°,AD=AB sin∠ABD=80×sin60°=80×=40(海里),
∵∠CAB=30°+45°=75°,
∴∠DAC=∠CAB﹣∠DAB=75°﹣30°=45°,
∴△ADC是等腰直角三角形,
∴AC=AD=×40=40(海里).
答:货船与港口A之间的距离是40海里.
17.解:过C作CH⊥AB于H,
根据题意,∠HBC=42°,∠HAC=37°,AB=22(nmile),
∵在Rt△CBH中,tan∠HBC=,
∴BH=.
∵在Rt△ACH中,tan∠HAC=,
∴AH=,
∵AB=AH+BH,
∴=AB.
∴CH=≈=9.00(nmile).
∵在Rt△CBH中,sin∠HBC=,
∴BC=≈13.4(nmile).
答:B处距离灯塔C的距离BC约为13.4nmile.
18.解:过D作DE⊥AB于E,DF⊥BC于F,如图所示:
由题意得:∠CDF=37°,CD=200米,
在Rt△CDF中,sin∠CDF==sin37°≈0.60,cos∠CDF==cos37°≈0.80,
∴CF≈200×0.60=120(米),DF≈200×0.80=160(米),
∵AB⊥BC,DF⊥BC,DE⊥AB,
∴∠B=∠DFB=∠DEB=90°,
∴四边形BFDE是矩形,
∴BF=DE,BE=DF=160米,
∴AE=AB﹣BE=300﹣160=140(米),
在Rt△ADE中,tan∠DAE==tan65°≈2.14,
∴DE≈AE×2.14=140×2.14=299.60(米),
∴BF=DE≈299.60(米),
∴BC=BF+CF=299.60+120≈420(米),
答:革命纪念碑与党史纪念馆之间的距离约为420米.
19.解:如图,过点B作BH⊥AC,垂足为H,
由题意得,∠BAC=60°,∠BCA=40°,AC=257海里,
在Rt△ABH中,
∵tan∠BAH=,cos∠BAH=,
∴BH=AH tan60°=AH,AB==2AH,
在Rt△BCH中,
∵tan∠BCH=,
∴CH==(海里),
又∵CA=CH+AH,
∴257=+AH,
所以AH=(海里),
∴AB=≈=168(海里),
答:AB的长约为168海里.
20.解:(1)如图,过点C作CH⊥AD,垂足为H.
由题意可知∠A=30°,∠AEC=45°,AE=35且AC=BC,
在Rt△CEH中,
∵∠CEH=45°,
∴CH=EH,
在Rt△ACH中,
∵∠A=30°,
∴AH=CH,
设AH=xkm,则EH=xkm,AH=xkm,
∵AE=35=AH+HE,
∴x+x=35,
解得x=,
即CH=EH=,
∴EC=CH=×=(km),
(2)在Rt△ACH中,
∵∠A=30°,
∴AC=2HC=(35﹣35)km,
在Rt△ABD中,
∵∠A=30°,
∴BD=AB=AC=BC=(35﹣35)km,
AD=BD=(35﹣35)=(105﹣35)km,
∴ED=AD﹣AE=(105﹣35)﹣35=(70﹣35)km,
答:海轮还要行驶(70﹣35)km才能到达位于港口B正西方向的D处.
