苏科版八年级数学上册 6.1函数(课件)(共22张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 6.1函数(课件)(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 14:31:01 | ||
图片预览




文档简介
(共22张PPT)
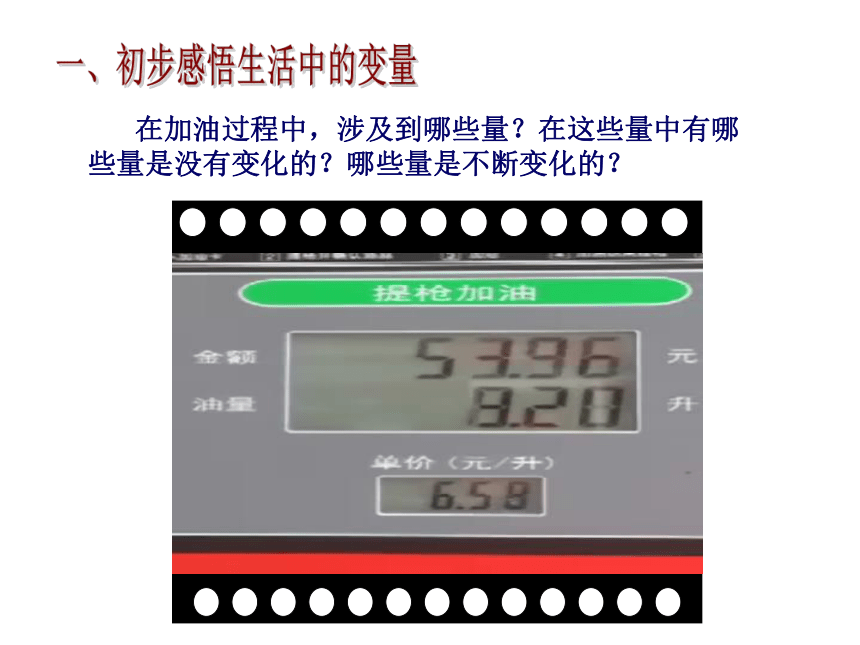
在加油过程中,涉及到哪些量?在这些量中有哪些量是没有变化的?哪些量是不断变化的?
请举出生活中的某些变化过程,并说
明其中的常量和变量。
油量
总金额
1
6.58
2
13.16
10
65.8
…
…
在加油过程中有哪几个变量?它们之间有什么关系?
1.变量总金额随着变量油量的变化而变化;
2.当油量的值确定时,总金额的值也确定;
3.对于油量的每一个值,总金额都有惟一值与它对应.
x
y
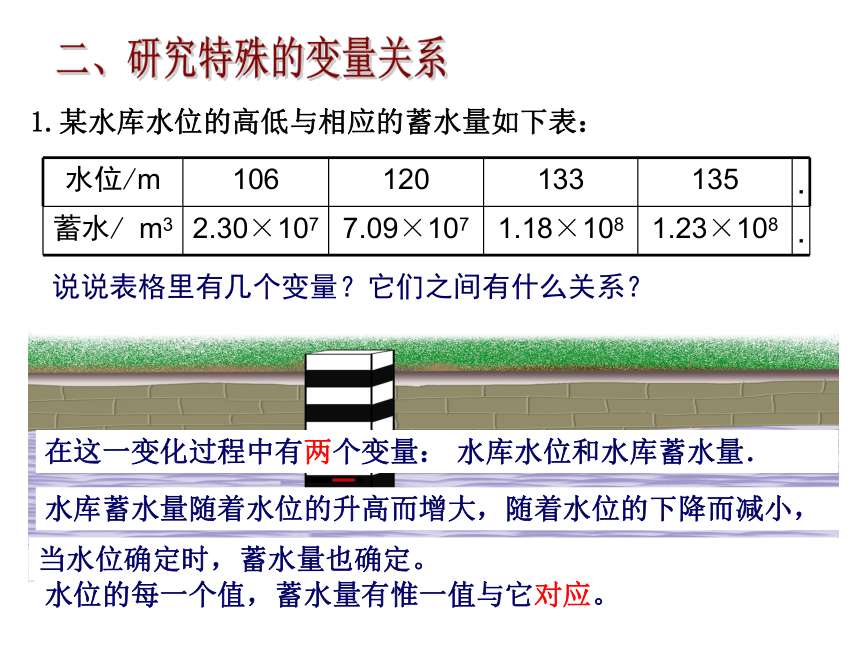
1.某水库水位的高低与相应的蓄水量如下表:
水位/m
106
120
133
135
…
蓄水/
m3
2.30×107
7.09×107
1.18×108
1.23×108
…
说说表格里有几个变量?它们之间有什么关系?
水库蓄水量随着水位的升高而增大,随着水位的下降而减小,
在这一变化过程中有两个变量:
水库水位和水库蓄水量.
当水位确定时,蓄水量也确定。
水位的每一个值,蓄水量有惟一值与它对应。
2.搭一条小鱼需要8根火柴棒,每多搭一条小鱼就要
增加6根火柴棒.
说说在这个过程中有哪几个变量?它们之间有什么关系?
(1)火柴棒的根数随着金鱼的条数的变化而变化;
(2)当金鱼的条数确定时,火柴棒的根数也确定;
(3)对于变量n的每一个值,变量S都有惟一值与它对应.
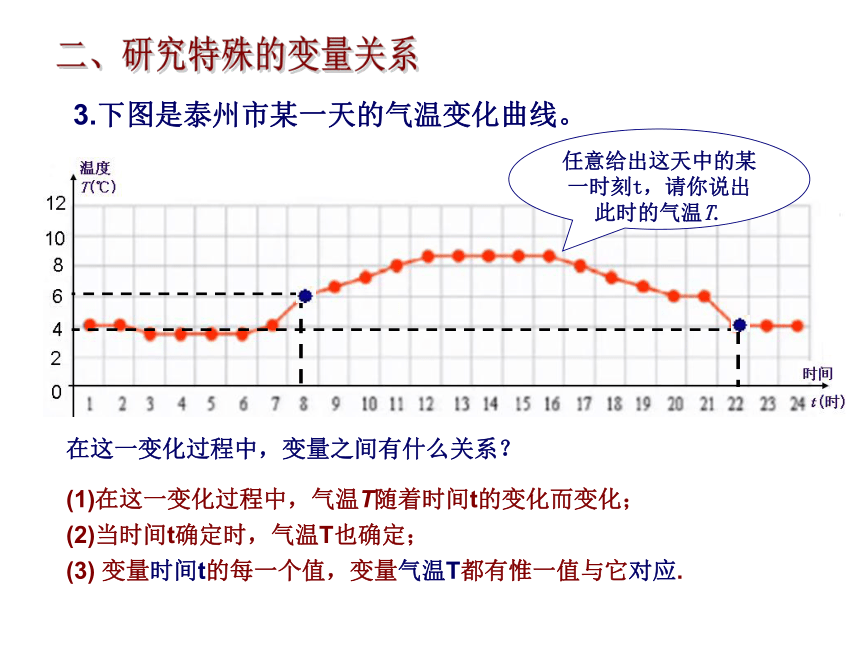
3.下图是泰州市某一天的气温变化曲线。
在这一变化过程中,变量之间有什么关系?
任意给出这天中的某一时刻t,请你说出此时的气温T.
(1)在这一变化过程中,气温T随着时间t的变化而变化;
(2)当时间t确定时,气温T也确定;
(3)
变量时间t的每一个值,变量气温T都有惟一值与它对应.
(1)有两个变量
;
(2)当其中一个变量变化时,另一个变量也随着发生变化;
(3)当其中一个变量确定时,另一个变量也随着确定.
x,y
对于
变量x的每一个值,变量y都有惟一值与它对应.
在一个变化过程中,
在这三个变化过程中,有哪些共同之处呢?
一般地,如果在一个变化的过程中有
两个变量x和y,并且对于变量x的每一个
值,变量y都有惟一的值与它对应,那么
我们称y是x的函数(function).其中,
x是自变量。
把一根20
cm长的铁丝围成一个长方形.
(1)当长方形的宽为3
cm时,长为多少?
(2)当长方形的宽为4
cm时,长为多少
(3)这个长方形的长是宽的函数吗?为什么?
解:(3)在这个变化过程中有两个变量“长”
和“宽”;“长”随着“宽”的变化而变化;且对于“宽”的每一个值,“长”都有唯一确定的值与之对应.
所以长方形的长是宽的函数.
如图,线段AB=6cm,D是线段AB上的一个定点,在垂直于AB的射线DE上有一个动点C(点C与点D不重合),分别连接CA、CB.
你能结合上面的背景提出问题吗?
生活
实例
数学
模型
研究
现实
函数:研究变化规律的数学模型
建构
应用
通过这节课的学习,你有哪些收获或疑惑?
1.必做题:课本P138页习题1、2题;
2.选做题:查阅关于函数的发展史。举出你身边函数的例子,并思考它们可以用怎样的形式进行表示?
在加油过程中,涉及到哪些量?在这些量中有哪些量是没有变化的?哪些量是不断变化的?
请举出生活中的某些变化过程,并说
明其中的常量和变量。
油量
总金额
1
6.58
2
13.16
10
65.8
…
…
在加油过程中有哪几个变量?它们之间有什么关系?
1.变量总金额随着变量油量的变化而变化;
2.当油量的值确定时,总金额的值也确定;
3.对于油量的每一个值,总金额都有惟一值与它对应.
x
y
1.某水库水位的高低与相应的蓄水量如下表:
水位/m
106
120
133
135
…
蓄水/
m3
2.30×107
7.09×107
1.18×108
1.23×108
…
说说表格里有几个变量?它们之间有什么关系?
水库蓄水量随着水位的升高而增大,随着水位的下降而减小,
在这一变化过程中有两个变量:
水库水位和水库蓄水量.
当水位确定时,蓄水量也确定。
水位的每一个值,蓄水量有惟一值与它对应。
2.搭一条小鱼需要8根火柴棒,每多搭一条小鱼就要
增加6根火柴棒.
说说在这个过程中有哪几个变量?它们之间有什么关系?
(1)火柴棒的根数随着金鱼的条数的变化而变化;
(2)当金鱼的条数确定时,火柴棒的根数也确定;
(3)对于变量n的每一个值,变量S都有惟一值与它对应.
3.下图是泰州市某一天的气温变化曲线。
在这一变化过程中,变量之间有什么关系?
任意给出这天中的某一时刻t,请你说出此时的气温T.
(1)在这一变化过程中,气温T随着时间t的变化而变化;
(2)当时间t确定时,气温T也确定;
(3)
变量时间t的每一个值,变量气温T都有惟一值与它对应.
(1)有两个变量
;
(2)当其中一个变量变化时,另一个变量也随着发生变化;
(3)当其中一个变量确定时,另一个变量也随着确定.
x,y
对于
变量x的每一个值,变量y都有惟一值与它对应.
在一个变化过程中,
在这三个变化过程中,有哪些共同之处呢?
一般地,如果在一个变化的过程中有
两个变量x和y,并且对于变量x的每一个
值,变量y都有惟一的值与它对应,那么
我们称y是x的函数(function).其中,
x是自变量。
把一根20
cm长的铁丝围成一个长方形.
(1)当长方形的宽为3
cm时,长为多少?
(2)当长方形的宽为4
cm时,长为多少
(3)这个长方形的长是宽的函数吗?为什么?
解:(3)在这个变化过程中有两个变量“长”
和“宽”;“长”随着“宽”的变化而变化;且对于“宽”的每一个值,“长”都有唯一确定的值与之对应.
所以长方形的长是宽的函数.
如图,线段AB=6cm,D是线段AB上的一个定点,在垂直于AB的射线DE上有一个动点C(点C与点D不重合),分别连接CA、CB.
你能结合上面的背景提出问题吗?
生活
实例
数学
模型
研究
现实
函数:研究变化规律的数学模型
建构
应用
通过这节课的学习,你有哪些收获或疑惑?
1.必做题:课本P138页习题1、2题;
2.选做题:查阅关于函数的发展史。举出你身边函数的例子,并思考它们可以用怎样的形式进行表示?
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
