苏科版八年级数学上册 6.1 函数(课件)(共19张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 6.1 函数(课件)(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 14:33:54 | ||
图片预览




文档简介
(共19张PPT)
6.1
函数
观察
在汽车加油的过程中,涉及到哪些数量?
观察
加完油后,汽车以45km/h的速度匀速开回家,在汽车行驶过程中,涉及到哪些数量?
在某一变化过程中,数值保持不变的量叫做常量,可以取不同数值的量叫做变量.
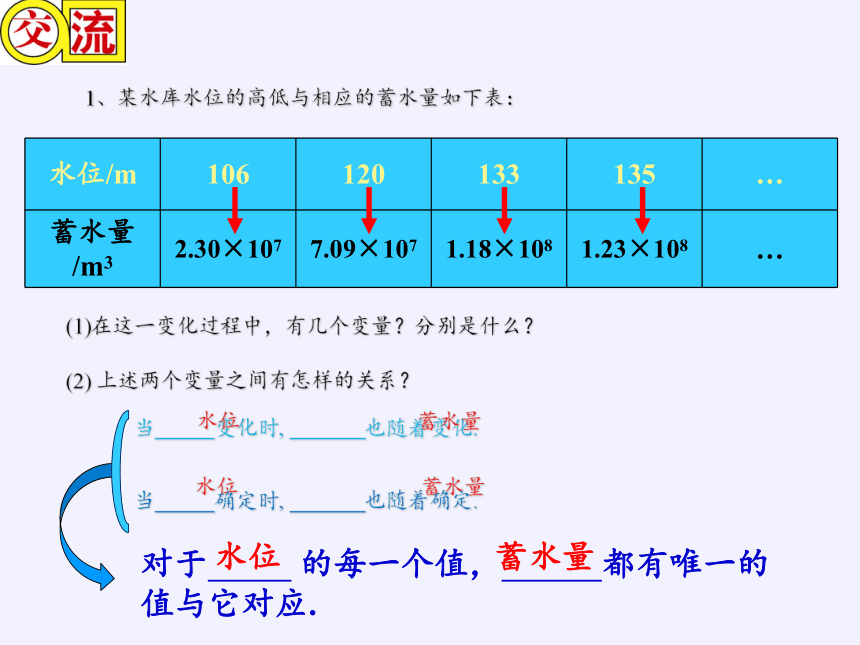
1、某水库水位的高低与相应的蓄水量如下表:
(1)在这一变化过程中,有几个变量?分别是什么?
(2)
上述两个变量之间有怎样的关系?
当
变化时,
也随着变化.
蓄水量
水位
蓄水量
水位
对于
的每一个值,
都有唯一的值与它对应.
水位
蓄水量
当
确定时,
也随着确定.
水位/m
106
120
133
135
…
蓄水量/m3
2.30×107
7.09×107
1.18×108
1.23×108
…
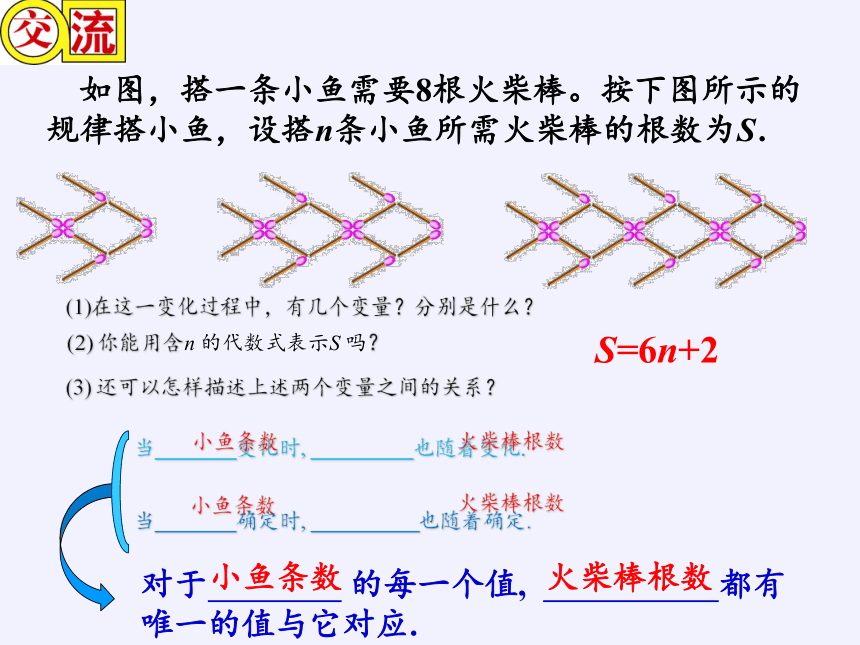
如图,搭一条小鱼需要8根火柴棒。按下图所示的规律搭小鱼,设搭n条小鱼所需火柴棒的根数为S.
(1)在这一变化过程中,有几个变量?分别是什么?
(3)
还可以怎样描述上述两个变量之间的关系?
当
变化时,
也随着变化.
火柴棒根数
小鱼条数
火柴棒根数
小鱼条数
对于
的每一个值,
都有唯一的值与它对应.
小鱼条数
火柴棒根数
当
确定时,
也随着确定.
(2)
你能用含n
的代数式表示S
吗?
S=6n+2
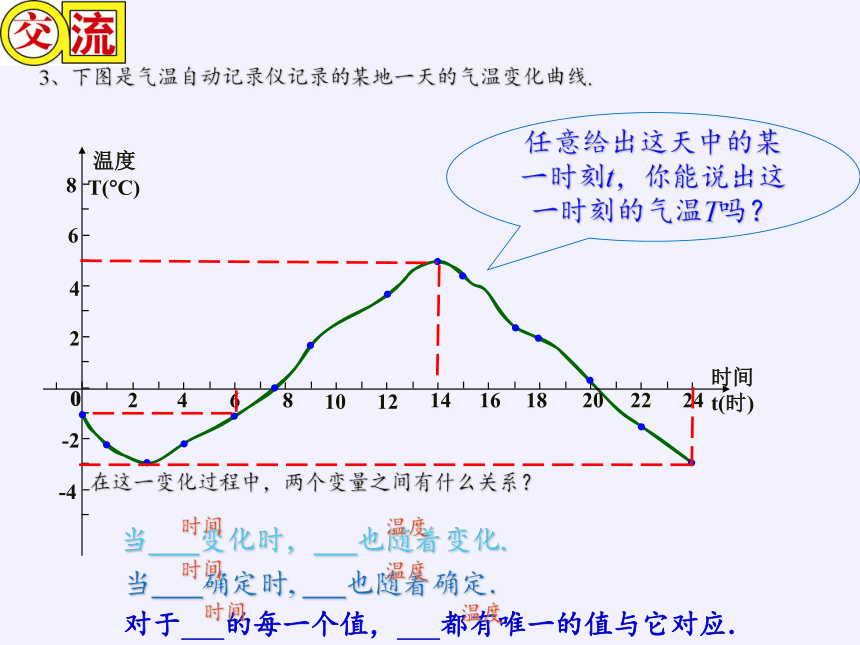
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
温度T( C)
2
4
6
8
-2
-4
0
3、下图是气温自动记录仪记录的某地一天的气温变化曲线.
当
变化时,
也随着变化.
任意给出这天中的某一时刻t,你能说出这一时刻的气温T吗?
对于
的每一个值,
都有唯一的值与它对应.
当
确定时,
也随着确定.
在这一变化过程中,两个变量之间有什么关系?
温度
时间
温度
时间
温度
时间
上述的三个变化过程,有怎样的共同之处呢?
说一说
函数的定义
一般地,
在一个变化过程中的两个变量x和y,
如果对于x的每一个值,
y都有唯一的值与它对应,那么我们称y是x的函数,x是自变量.
说一说
上述三个实例中,谁是谁的函数?自变量是谁?
水位
蓄水量
小鱼条数
火柴棒根数
温度
时间
变量
例1、用一根1m长的铁丝围成一个长方形.
(1)当长方形的宽为0.1m时,长为
m
.
(2)当长方形的宽为0.2m时,长为
m
.
(3)当长方形的宽为
x
m时,长为
m
.
(4)长方形的长y(m)是宽
x
(m)的函数吗?
为什么?
长方形的长y是宽x的函数.
理由:在这个变化过程中,有两个变量x和y,并且对于x的每一个值,y都有唯一的值与它对应.
0.3
0.4
(0.5-x)
一石激起千层浪,水滴泛起层层波.
例2.水滴激起的波纹可以看作是一个不断向外扩展的圆.在这一变化过程中,你能找到函数关系吗?
请自己编一个表示函数关系的实例.
小组交流的要求:
1、每个人轮流说说自己编的函数实例,要求讲清谁是谁的函数?自变量是什么?
2、一个同学说的时候,其他同学判断这两个变量之间的关系是不是函数关系?
在学习了函数的概念后,同学们试着自己举一些函数的实例:
小颖:汽油每升7.75元,加油x升的总价为y元,则y是x的函数,其中x是自变量.
你认为他们说的正确吗?为什么?
小亮:长方体的长是a,宽是b,高是4,长方体的体积V是长a的函数.
例3.根据表格中的信息,回答问题:其中,x表示乘公交车的站数(站),y表示相应付的票价(元).
(1)y是x的函数吗 为什么?
x
1
2
3
4
5
6
7
8
9
10
11
12
13
14
y
1.0
1.0
1.0
1.0
1.2
1.2
1.5
1.5
1.5
1.8
1.8
1.8
2.0
2.0
(2)x是y的函数吗 为什么?
信件质量x/克
0<
x
≤20
20<
x
≤40
40<
x
≤60
邮资y
/元
0.80
1.20
1.60
在国内投寄平信应付邮资如下表:
变式:
(1)y是x的函数吗 为什么?
(2)x是y的函数吗 为什么?
1、本节课,你有哪些收获?
2、本节课,给你感受最深的是什么?你还有哪些困惑?
作业:
2.
选做题:查阅关于函数的发展历史.
1.
必做题:课本第138页练习的第1、2题;
谢
谢
6.1
函数
观察
在汽车加油的过程中,涉及到哪些数量?
观察
加完油后,汽车以45km/h的速度匀速开回家,在汽车行驶过程中,涉及到哪些数量?
在某一变化过程中,数值保持不变的量叫做常量,可以取不同数值的量叫做变量.
1、某水库水位的高低与相应的蓄水量如下表:
(1)在这一变化过程中,有几个变量?分别是什么?
(2)
上述两个变量之间有怎样的关系?
当
变化时,
也随着变化.
蓄水量
水位
蓄水量
水位
对于
的每一个值,
都有唯一的值与它对应.
水位
蓄水量
当
确定时,
也随着确定.
水位/m
106
120
133
135
…
蓄水量/m3
2.30×107
7.09×107
1.18×108
1.23×108
…
如图,搭一条小鱼需要8根火柴棒。按下图所示的规律搭小鱼,设搭n条小鱼所需火柴棒的根数为S.
(1)在这一变化过程中,有几个变量?分别是什么?
(3)
还可以怎样描述上述两个变量之间的关系?
当
变化时,
也随着变化.
火柴棒根数
小鱼条数
火柴棒根数
小鱼条数
对于
的每一个值,
都有唯一的值与它对应.
小鱼条数
火柴棒根数
当
确定时,
也随着确定.
(2)
你能用含n
的代数式表示S
吗?
S=6n+2
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
温度T( C)
2
4
6
8
-2
-4
0
3、下图是气温自动记录仪记录的某地一天的气温变化曲线.
当
变化时,
也随着变化.
任意给出这天中的某一时刻t,你能说出这一时刻的气温T吗?
对于
的每一个值,
都有唯一的值与它对应.
当
确定时,
也随着确定.
在这一变化过程中,两个变量之间有什么关系?
温度
时间
温度
时间
温度
时间
上述的三个变化过程,有怎样的共同之处呢?
说一说
函数的定义
一般地,
在一个变化过程中的两个变量x和y,
如果对于x的每一个值,
y都有唯一的值与它对应,那么我们称y是x的函数,x是自变量.
说一说
上述三个实例中,谁是谁的函数?自变量是谁?
水位
蓄水量
小鱼条数
火柴棒根数
温度
时间
变量
例1、用一根1m长的铁丝围成一个长方形.
(1)当长方形的宽为0.1m时,长为
m
.
(2)当长方形的宽为0.2m时,长为
m
.
(3)当长方形的宽为
x
m时,长为
m
.
(4)长方形的长y(m)是宽
x
(m)的函数吗?
为什么?
长方形的长y是宽x的函数.
理由:在这个变化过程中,有两个变量x和y,并且对于x的每一个值,y都有唯一的值与它对应.
0.3
0.4
(0.5-x)
一石激起千层浪,水滴泛起层层波.
例2.水滴激起的波纹可以看作是一个不断向外扩展的圆.在这一变化过程中,你能找到函数关系吗?
请自己编一个表示函数关系的实例.
小组交流的要求:
1、每个人轮流说说自己编的函数实例,要求讲清谁是谁的函数?自变量是什么?
2、一个同学说的时候,其他同学判断这两个变量之间的关系是不是函数关系?
在学习了函数的概念后,同学们试着自己举一些函数的实例:
小颖:汽油每升7.75元,加油x升的总价为y元,则y是x的函数,其中x是自变量.
你认为他们说的正确吗?为什么?
小亮:长方体的长是a,宽是b,高是4,长方体的体积V是长a的函数.
例3.根据表格中的信息,回答问题:其中,x表示乘公交车的站数(站),y表示相应付的票价(元).
(1)y是x的函数吗 为什么?
x
1
2
3
4
5
6
7
8
9
10
11
12
13
14
y
1.0
1.0
1.0
1.0
1.2
1.2
1.5
1.5
1.5
1.8
1.8
1.8
2.0
2.0
(2)x是y的函数吗 为什么?
信件质量x/克
0<
x
≤20
20<
x
≤40
40<
x
≤60
邮资y
/元
0.80
1.20
1.60
在国内投寄平信应付邮资如下表:
变式:
(1)y是x的函数吗 为什么?
(2)x是y的函数吗 为什么?
1、本节课,你有哪些收获?
2、本节课,给你感受最深的是什么?你还有哪些困惑?
作业:
2.
选做题:查阅关于函数的发展历史.
1.
必做题:课本第138页练习的第1、2题;
谢
谢
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
