苏科版八年级数学上册 5.2 平面直角坐标系课件(40张ppt)
文档属性
| 名称 | 苏科版八年级数学上册 5.2 平面直角坐标系课件(40张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 14:41:35 | ||
图片预览




文档简介
(共40张PPT)
平面直角坐标系
北京西路
北京东路
中山北路
中山南路
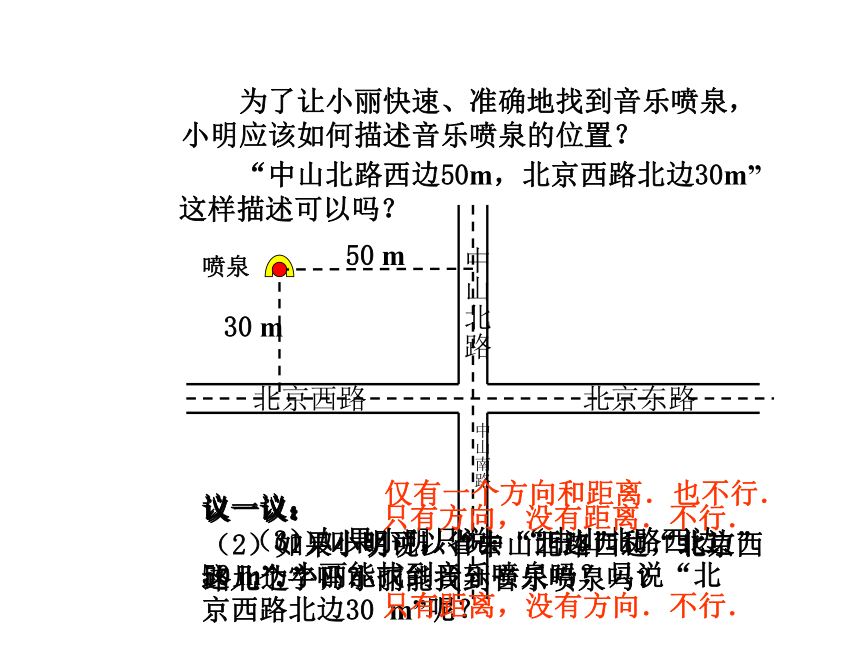
“中山北路西边50m,北京西路北边30m”这样描述可以吗?
50
m
30
m
议一议:
(1)小明可以省去“西边”和“北边”这几个字吗?
议一议:
(2)如果小明说:“中山北路西边,北京西路北边”,小丽能找到音乐喷泉吗?
议一议:
(3)如果小明只说:“中山北路西边50
m”,
小丽能找到音乐喷泉吗?只说“北京西路北边30
m”呢?
为了让小丽快速、准确地找到音乐喷泉,小明应该如何描述音乐喷泉的位置?
喷泉
只有距离,没有方向.不行.
只有方向,没有距离.不行.
仅有一个方向和距离.也不行.
我们曾经利用数轴上的实数来表示直线上的点。
思考:
类似地,能否找到一种方法来表示平面内点的位置呢?
北京西路
北京东路
中山北路
中山南路
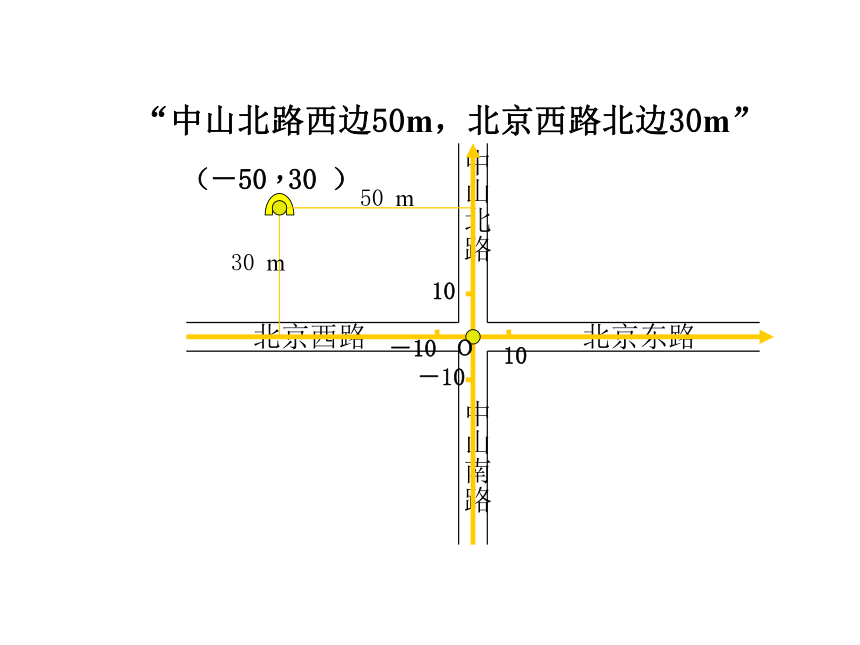
“中山北路西边50m,北京西路北边30m”
50
m
30
m
-10
10
10
-10
O
-50
30
(
)
,
北京西路
北京东路
中山北路
中山南路
-10
10
10
-10
O
50m
20m
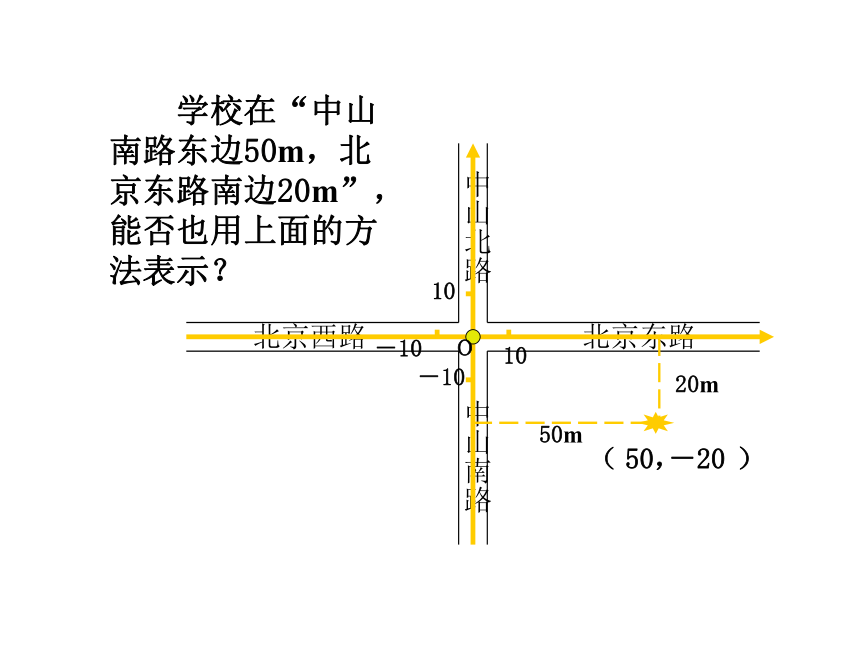
学校在“中山南路东边50m,北京东路南边20m”,能否也用上面的方法表示?
(
-20
,
50
)
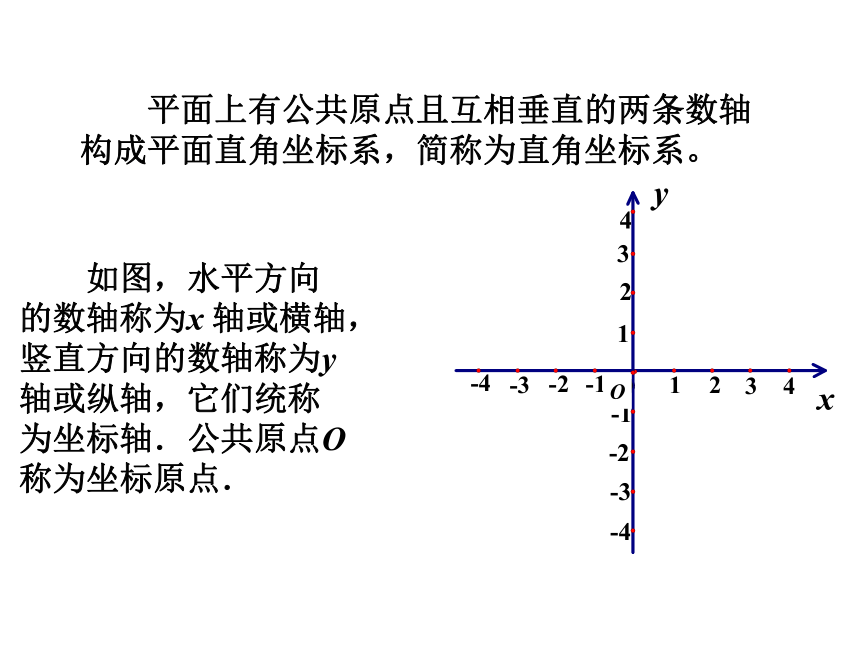
平面上有公共原点且互相垂直的两条数轴构成平面直角坐标系,简称为直角坐标系。
如图,水平方向的数轴称为x
轴或横轴,竖直方向的数轴称为y
轴或纵轴,它们统称为坐标轴.公共原点O称为坐标原点.
x
y
x
y
O
x
y
x
y
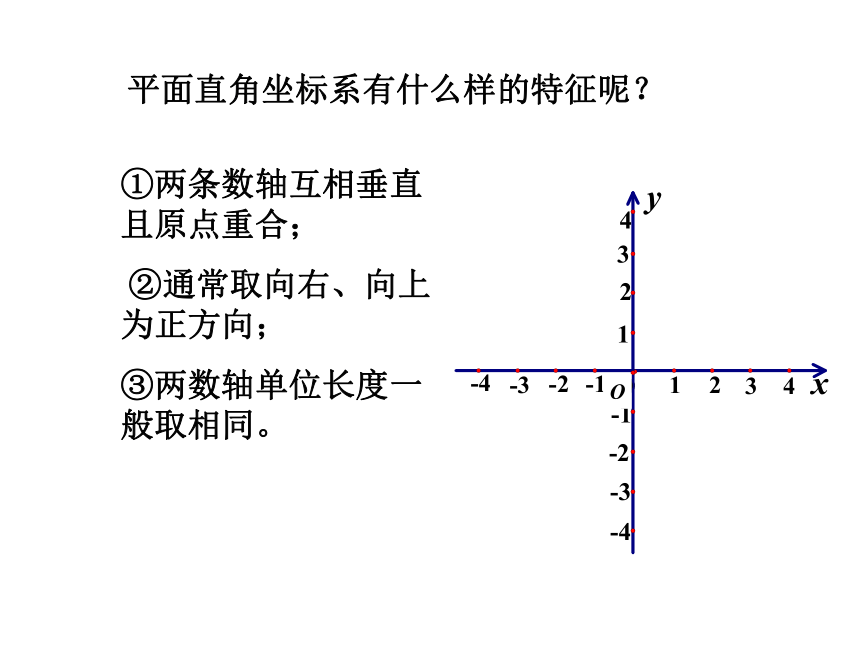
平面直角坐标系有什么样的特征呢?
①两条数轴互相垂直且原点重合;
②通常取向右、向上为正方向;
③两数轴单位长度一般取相同。
x
y
O
北京西路
北京东路
中山北路
中山南路
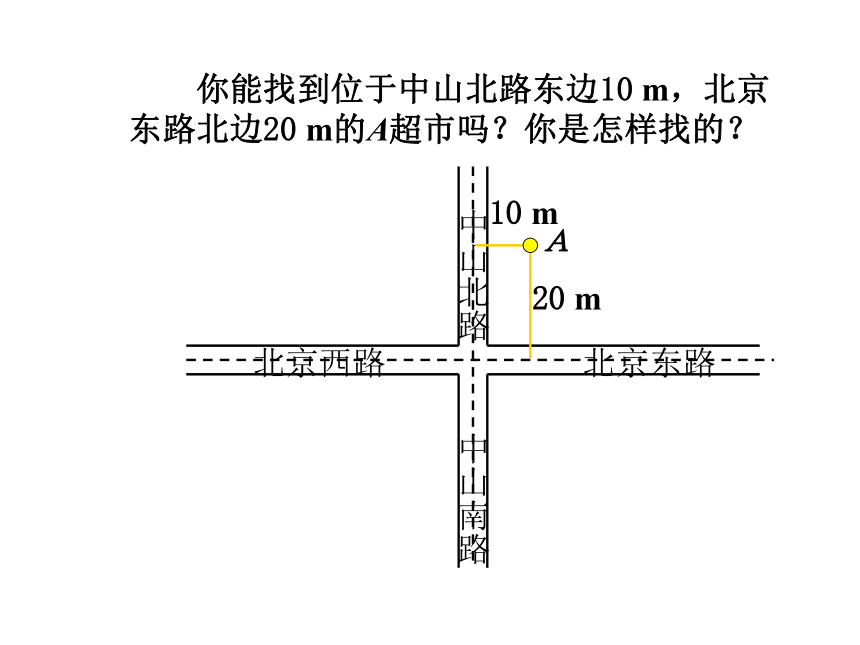
你能找到位于中山北路东边10
m,北京东路北边20
m的A超市吗?你是怎样找的?
10
m
20
m
A
北京西路
北京东路
中山北路
中山南路
-10
10
10
-10
O
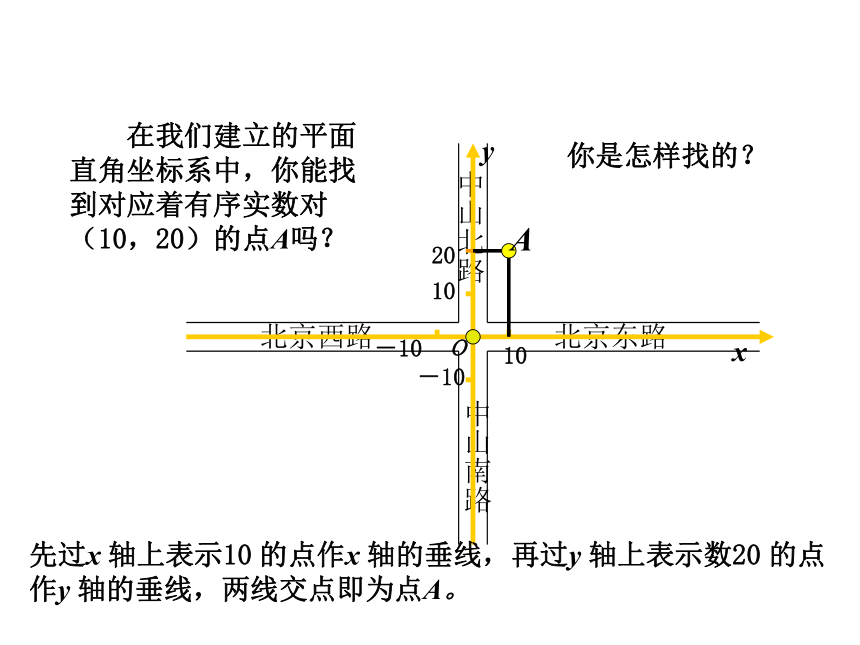
在我们建立的平面直角坐标系中,你能找到对应着有序实数对(10,20)的点A吗?
20
A
x
y
先过x
轴上表示10
的点作x
轴的垂线,再过y
轴上表示数20
的点作y
轴的垂线,两线交点即为点A。
你是怎样找的?
通过上面的讨论,你有什么发现?
在直角坐标系内,点与有序实数对
具有怎样的关系?
在直角坐标系中,一对有序实数可以确定一个点的位置;反之,任意一点都可以用一对有序实数表示。
我们称这样的有序实数对叫做点的
坐标。
下面来认识点的坐标。
在平面直角坐标系中,有序实数对(a,b)描述的是一个点
P
的位置,该如何确定点
P
的位置呢?
y
o
-1
1
-1
1
a
b
P
过
x
轴上表示
a的点作
x
轴的垂线,再过
y
轴上表示
b
的点作
y
轴的垂线,两线的交点即为点
P
.
x
x
y
o
-1
1
-1
1
m
n
Q
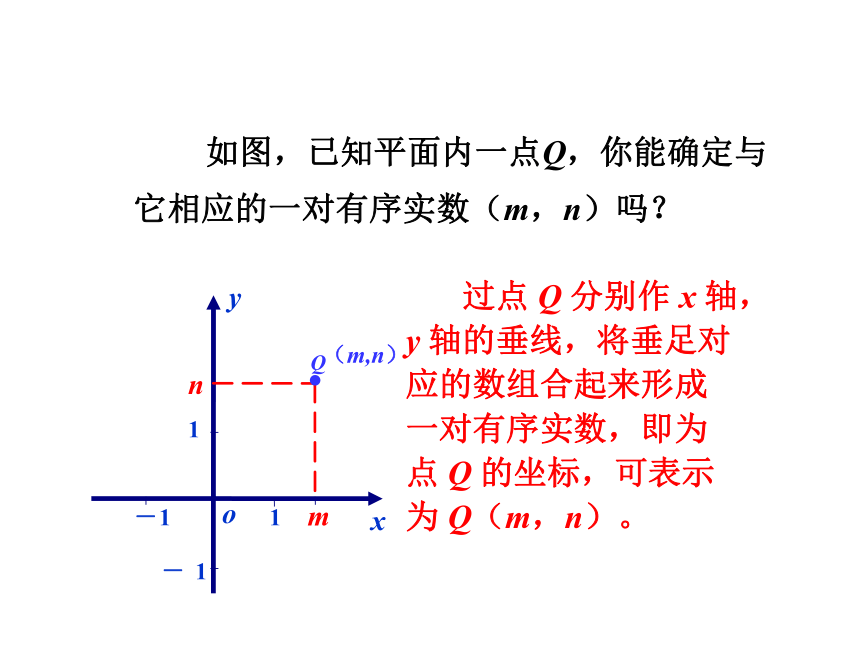
如图,已知平面内一点Q,你能确定与它相应的一对有序实数(m,n)吗?
(m,n)
过点
Q
分别作
x
轴,y
轴的垂线,将垂足对应的数组合起来形成一对有序实数,即为点
Q
的坐标,可表示为
Q(m,n)。
1.在平面直角坐标系中,一对有序实数可以确
定一个点的位置;反之,任意一点的位置都可以用一对有序实数来表示。这样的有序实数对叫做点的坐标。
2.点的坐标通常与表示该点的大写字母写在一起,如
P(a,b),Q(m,n)。
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
(4,1)
B
(-1,4)
C
D
例1
在直角坐标系中,描出下列各点的位置:
A(4,1),B(-1,4),C(-4,-2),D(3,-2),
E(0,1
),F(
-4,0
)
。
x
(-4,-2)
E
(0,1)
F
(-4,0)
(3,-2)
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
例
2 写出图中点A、B、C
的坐标。
x
.
A
.
.
B
C
(-4,3)
(-3,-2)
(1
,-3)
第一象限
第二象限
第四象限
第三象限
注意:坐标轴上的点不在任一象限内。
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
(4,1)
B
(-1,4)
C
D
E
你能指出点A、B、C、D分别在第几象限吗?点E、F呢?
x
(-4,-2)
(0,1)
F
(-4,0)
(3,-2)
(+,+)
(-,+)
(-,-)
(+,-)
在x轴上的点,纵坐标等于0;
在y轴上的点,横坐标等于0;
探索点的坐标的几何意义:
已知点A(a,b),过点A作x轴的垂线,垂足为B,过点A作y轴的垂线,垂足为C。
(1)
四边形OBAC是矩形吗?
(2)
线段AB的长度与点A的坐标有什么数量关系?
(3)
线段AC的长度与点A的坐标有什么数量关系?
是
线段AB的长度等于b
线段AC的长度等于a
三、已知
P
点坐标为(2
a
+
1,a-3)
(
1
)
点
P
在
x
轴上,则
a=
;
(
2
)
点
P
在
y
轴上,则
a=
;
四、若点
P(x,y)在第四象限,|
x
|=5,|
y
|=4,则
P
点的坐标为
。
3
(5,-4)
1.什么是平面直角坐标系
2.平面内点的坐标的意义,你理解了吗
3.在学习过程中你还存在哪些问题
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
讨论:已知点A(-1,0)、B(-5,0)、C(-3,5)。
(1)在下面的直角坐标系中画出这三点。
(2)
画出△ABC及BC边上的高AD。
(3)
△ABC是等腰三角形吗?AD的长是多少?
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
B
C
例
3
如图,点B、点C在x轴上,试在第一象限内画
等腰三角形ABC,使它的底边为BC
,面积为10,并
写出△ABC各顶点的坐标。
x
.
.
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
B
C
解:点B、点C的坐标分别为B(1,0)、C(5,0)。
因为BC=4,△ABC面积为10,所以△ABC的高为5。
x
.
.
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
B
C
解:点B、点C的坐标分别为B(1,0)、C(5,0)。
因为BC=4,△ABC面积为10,所以△ABC的高为5。
又因为△ABC是等腰三角形,所以点A的横坐标
是3,
纵坐标是5,即A(3,5)。
在第一象限内画出△ABC。
x
A
.
.
.
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
B
C
讨论:把△ABC沿y轴翻折得到△A′B′C′,你能写出
△A′B′C′各顶点的坐标吗?
x
A
A′
.
.
.
.
.
.
C′
B′
A′
(-3,5)
B′
(-1,0)
C′
(-5,0)
.
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
B′
C′
再讨论:再把△A′B′C′向下平移3个单位长度得到
△A′′B′′C′′,你能写出△A′′B′′C′′各顶点的坐标吗?
x
A′
A′′
.
.
.
.
.
C′′
B′′
A′′(-3,2)
B
′′
(-1,-3)
C
′′
(-5,-3)
.
.
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
5
-1
-2
-3
-4
-5
x
4
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
观察图形,填空:
(1)点(1,-3)关于x轴对称的点的坐标为________,
关于y轴对称的点的坐标为_________ ,
关于原点对称的点的坐标为
_________。
(2)点(-1,3)关于x轴对称的点的坐标为___________,
关于y
轴对称的点的坐标为______
,
关于原点对称的点的坐标为_________。
(3)点P(a
,
b)关于x轴对称点的坐标为
________,
关于y轴对称的点的坐标为_________,
关于原点对称的点的坐标为____________
。
(1,3)
(-1,-3)
(-1,3)
(-1,-3)
(1,3)
(1,-3)
(a,-b)
(-a,b)
(-a,-b)
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
5
-1
-2
-3
-4
-5
x
4
A(-4,1)
B(-2,3)
(3,1)
(5,3)
A′(3,3)
B′(5,5)
.
.
.
.
如果点C
(
m
,n
)
是线段AB上的任意一点,那么当AB平移到
A′
B′
后,与点
C
对应的点
C′
的坐标是_________________。
(m+7,
n+2)
1.填空
(1)平行于
x
轴的直线上不同的两个点的__坐标相同,
__坐标不同;平行于
y
轴的直线上不同的两个点的
__坐标相同,__坐标不同。
(2)点
P
(a,b),关于
x
轴对称的点的坐标为________,
关于
y
轴对称的点的坐标为__________
。
(3)图形左右平移,对应点的__坐标变化,__坐标
不变;图形上下平移,对应点的__坐标变化,
__坐标不变。
纵
横
横
纵
(a,-b)
(-a,b)
横
纵
纵
横
在学习小组中总结一下你本节课的收获吧!
电视机厂通过电脑控制的机械手,把各种元件准确
插入线路板的孔眼中,然后通过焊接工序将它们焊牢。
如果你是工程师,那么你是怎样向机械手下达指令,让它把元件准确插入相应的孔眼中?
可以建立适当的平面直角坐标系,如本图中,
点
A
的坐标为(
a,d
)
,
点
B
的坐标为
(b,c
)
。
站在中心广场,你能根据这张旅游景点分布图,
说出各个景点的位置吗
若利用图中的
方格,建立直角坐
标系呢?
(0,0)
(5,7)
(-8,5)
(-11,1)
(-8,-3)
(-12,-8)
(3,-6)
x
y
O
y
x
o
x
y
o
y
x
o
y
o
x
例4
如图,已知正方形
ABCD
的边长为4,建立
适当的直角坐标系,分别写出各顶点的坐标.
C
A
B
C
D
能建立不同的直角坐标系,表示正方形各顶点的坐标吗?
A
B
C
A
B
C
D
y
O
x
A
B
C
D
O
x
y
A
B
C
D
O
x
y
y
x
A
B
C
D
O
在一次“寻宝”游戏中,寻宝人员已经找到了坐
标为(3,2)和(3,-2)的两个标志点,并且知道
藏宝地点坐标为(4,4),除此之外不知道其他信息,
你能在图中画出这个坐标系吗?
(4,4)
(3,-2)
(3,2)
x
y
O
在学习小组中总结一下你本节课的收获吧!
平面直角坐标系
北京西路
北京东路
中山北路
中山南路
“中山北路西边50m,北京西路北边30m”这样描述可以吗?
50
m
30
m
议一议:
(1)小明可以省去“西边”和“北边”这几个字吗?
议一议:
(2)如果小明说:“中山北路西边,北京西路北边”,小丽能找到音乐喷泉吗?
议一议:
(3)如果小明只说:“中山北路西边50
m”,
小丽能找到音乐喷泉吗?只说“北京西路北边30
m”呢?
为了让小丽快速、准确地找到音乐喷泉,小明应该如何描述音乐喷泉的位置?
喷泉
只有距离,没有方向.不行.
只有方向,没有距离.不行.
仅有一个方向和距离.也不行.
我们曾经利用数轴上的实数来表示直线上的点。
思考:
类似地,能否找到一种方法来表示平面内点的位置呢?
北京西路
北京东路
中山北路
中山南路
“中山北路西边50m,北京西路北边30m”
50
m
30
m
-10
10
10
-10
O
-50
30
(
)
,
北京西路
北京东路
中山北路
中山南路
-10
10
10
-10
O
50m
20m
学校在“中山南路东边50m,北京东路南边20m”,能否也用上面的方法表示?
(
-20
,
50
)
平面上有公共原点且互相垂直的两条数轴构成平面直角坐标系,简称为直角坐标系。
如图,水平方向的数轴称为x
轴或横轴,竖直方向的数轴称为y
轴或纵轴,它们统称为坐标轴.公共原点O称为坐标原点.
x
y
x
y
O
x
y
x
y
平面直角坐标系有什么样的特征呢?
①两条数轴互相垂直且原点重合;
②通常取向右、向上为正方向;
③两数轴单位长度一般取相同。
x
y
O
北京西路
北京东路
中山北路
中山南路
你能找到位于中山北路东边10
m,北京东路北边20
m的A超市吗?你是怎样找的?
10
m
20
m
A
北京西路
北京东路
中山北路
中山南路
-10
10
10
-10
O
在我们建立的平面直角坐标系中,你能找到对应着有序实数对(10,20)的点A吗?
20
A
x
y
先过x
轴上表示10
的点作x
轴的垂线,再过y
轴上表示数20
的点作y
轴的垂线,两线交点即为点A。
你是怎样找的?
通过上面的讨论,你有什么发现?
在直角坐标系内,点与有序实数对
具有怎样的关系?
在直角坐标系中,一对有序实数可以确定一个点的位置;反之,任意一点都可以用一对有序实数表示。
我们称这样的有序实数对叫做点的
坐标。
下面来认识点的坐标。
在平面直角坐标系中,有序实数对(a,b)描述的是一个点
P
的位置,该如何确定点
P
的位置呢?
y
o
-1
1
-1
1
a
b
P
过
x
轴上表示
a的点作
x
轴的垂线,再过
y
轴上表示
b
的点作
y
轴的垂线,两线的交点即为点
P
.
x
x
y
o
-1
1
-1
1
m
n
Q
如图,已知平面内一点Q,你能确定与它相应的一对有序实数(m,n)吗?
(m,n)
过点
Q
分别作
x
轴,y
轴的垂线,将垂足对应的数组合起来形成一对有序实数,即为点
Q
的坐标,可表示为
Q(m,n)。
1.在平面直角坐标系中,一对有序实数可以确
定一个点的位置;反之,任意一点的位置都可以用一对有序实数来表示。这样的有序实数对叫做点的坐标。
2.点的坐标通常与表示该点的大写字母写在一起,如
P(a,b),Q(m,n)。
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
(4,1)
B
(-1,4)
C
D
例1
在直角坐标系中,描出下列各点的位置:
A(4,1),B(-1,4),C(-4,-2),D(3,-2),
E(0,1
),F(
-4,0
)
。
x
(-4,-2)
E
(0,1)
F
(-4,0)
(3,-2)
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
例
2 写出图中点A、B、C
的坐标。
x
.
A
.
.
B
C
(-4,3)
(-3,-2)
(1
,-3)
第一象限
第二象限
第四象限
第三象限
注意:坐标轴上的点不在任一象限内。
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
(4,1)
B
(-1,4)
C
D
E
你能指出点A、B、C、D分别在第几象限吗?点E、F呢?
x
(-4,-2)
(0,1)
F
(-4,0)
(3,-2)
(+,+)
(-,+)
(-,-)
(+,-)
在x轴上的点,纵坐标等于0;
在y轴上的点,横坐标等于0;
探索点的坐标的几何意义:
已知点A(a,b),过点A作x轴的垂线,垂足为B,过点A作y轴的垂线,垂足为C。
(1)
四边形OBAC是矩形吗?
(2)
线段AB的长度与点A的坐标有什么数量关系?
(3)
线段AC的长度与点A的坐标有什么数量关系?
是
线段AB的长度等于b
线段AC的长度等于a
三、已知
P
点坐标为(2
a
+
1,a-3)
(
1
)
点
P
在
x
轴上,则
a=
;
(
2
)
点
P
在
y
轴上,则
a=
;
四、若点
P(x,y)在第四象限,|
x
|=5,|
y
|=4,则
P
点的坐标为
。
3
(5,-4)
1.什么是平面直角坐标系
2.平面内点的坐标的意义,你理解了吗
3.在学习过程中你还存在哪些问题
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
讨论:已知点A(-1,0)、B(-5,0)、C(-3,5)。
(1)在下面的直角坐标系中画出这三点。
(2)
画出△ABC及BC边上的高AD。
(3)
△ABC是等腰三角形吗?AD的长是多少?
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
B
C
例
3
如图,点B、点C在x轴上,试在第一象限内画
等腰三角形ABC,使它的底边为BC
,面积为10,并
写出△ABC各顶点的坐标。
x
.
.
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
B
C
解:点B、点C的坐标分别为B(1,0)、C(5,0)。
因为BC=4,△ABC面积为10,所以△ABC的高为5。
x
.
.
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
B
C
解:点B、点C的坐标分别为B(1,0)、C(5,0)。
因为BC=4,△ABC面积为10,所以△ABC的高为5。
又因为△ABC是等腰三角形,所以点A的横坐标
是3,
纵坐标是5,即A(3,5)。
在第一象限内画出△ABC。
x
A
.
.
.
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
B
C
讨论:把△ABC沿y轴翻折得到△A′B′C′,你能写出
△A′B′C′各顶点的坐标吗?
x
A
A′
.
.
.
.
.
.
C′
B′
A′
(-3,5)
B′
(-1,0)
C′
(-5,0)
.
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
B′
C′
再讨论:再把△A′B′C′向下平移3个单位长度得到
△A′′B′′C′′,你能写出△A′′B′′C′′各顶点的坐标吗?
x
A′
A′′
.
.
.
.
.
C′′
B′′
A′′(-3,2)
B
′′
(-1,-3)
C
′′
(-5,-3)
.
.
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
5
-1
-2
-3
-4
-5
x
4
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
观察图形,填空:
(1)点(1,-3)关于x轴对称的点的坐标为________,
关于y轴对称的点的坐标为_________ ,
关于原点对称的点的坐标为
_________。
(2)点(-1,3)关于x轴对称的点的坐标为___________,
关于y
轴对称的点的坐标为______
,
关于原点对称的点的坐标为_________。
(3)点P(a
,
b)关于x轴对称点的坐标为
________,
关于y轴对称的点的坐标为_________,
关于原点对称的点的坐标为____________
。
(1,3)
(-1,-3)
(-1,3)
(-1,-3)
(1,3)
(1,-3)
(a,-b)
(-a,b)
(-a,-b)
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
5
-1
-2
-3
-4
-5
x
4
A(-4,1)
B(-2,3)
(3,1)
(5,3)
A′(3,3)
B′(5,5)
.
.
.
.
如果点C
(
m
,n
)
是线段AB上的任意一点,那么当AB平移到
A′
B′
后,与点
C
对应的点
C′
的坐标是_________________。
(m+7,
n+2)
1.填空
(1)平行于
x
轴的直线上不同的两个点的__坐标相同,
__坐标不同;平行于
y
轴的直线上不同的两个点的
__坐标相同,__坐标不同。
(2)点
P
(a,b),关于
x
轴对称的点的坐标为________,
关于
y
轴对称的点的坐标为__________
。
(3)图形左右平移,对应点的__坐标变化,__坐标
不变;图形上下平移,对应点的__坐标变化,
__坐标不变。
纵
横
横
纵
(a,-b)
(-a,b)
横
纵
纵
横
在学习小组中总结一下你本节课的收获吧!
电视机厂通过电脑控制的机械手,把各种元件准确
插入线路板的孔眼中,然后通过焊接工序将它们焊牢。
如果你是工程师,那么你是怎样向机械手下达指令,让它把元件准确插入相应的孔眼中?
可以建立适当的平面直角坐标系,如本图中,
点
A
的坐标为(
a,d
)
,
点
B
的坐标为
(b,c
)
。
站在中心广场,你能根据这张旅游景点分布图,
说出各个景点的位置吗
若利用图中的
方格,建立直角坐
标系呢?
(0,0)
(5,7)
(-8,5)
(-11,1)
(-8,-3)
(-12,-8)
(3,-6)
x
y
O
y
x
o
x
y
o
y
x
o
y
o
x
例4
如图,已知正方形
ABCD
的边长为4,建立
适当的直角坐标系,分别写出各顶点的坐标.
C
A
B
C
D
能建立不同的直角坐标系,表示正方形各顶点的坐标吗?
A
B
C
A
B
C
D
y
O
x
A
B
C
D
O
x
y
A
B
C
D
O
x
y
y
x
A
B
C
D
O
在一次“寻宝”游戏中,寻宝人员已经找到了坐
标为(3,2)和(3,-2)的两个标志点,并且知道
藏宝地点坐标为(4,4),除此之外不知道其他信息,
你能在图中画出这个坐标系吗?
(4,4)
(3,-2)
(3,2)
x
y
O
在学习小组中总结一下你本节课的收获吧!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
