2021--2022学年人教版九年级数学上册24.4 弧长和扇形面积 课件(20张)
文档属性
| 名称 | 2021--2022学年人教版九年级数学上册24.4 弧长和扇形面积 课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 10:38:40 | ||
图片预览








文档简介
(共20张PPT)
24.4
弧长和扇形面积
第1课时
弧长和扇形面积
一
学习目标
1.
以圆的周长和面积为基础,探究弧长和扇形的面积公式,并会用来计算弧长和扇形面积.
2.
能利用弧长、扇形面积计算公式计算简单组合图形的周长和面积.
二
重难点
重点:经历探究弧长和扇形面积公式的过程.能够推导公式.
难点:用公式解决实际问题.
1.情景导入
三
教学过程
中国是世界上最早使用扇子的国家.
自扇子传世以来,相关的趣闻轶事多不胜数;随着时代的发展,扇子不仅仅是一种纳凉工具,更是一种备受人们喜爱的工艺品.
如图,
扇子面的纸张面积如何计算,外围弧长又如何计算
2.探究新知
问题
1
我们知道弧是圆的一部分,弧长就是圆周长的一部分.想一想,如何计算圆周长 圆的周长可以看作是多少度的圆心角所对的弧长 由此发现,1°的圆心角所对的弧长是多少
n°的圆心角呢
解:在半径为R的圆中,因为360°的圆心角所对的弧长就是圆周长C=2πR,所以1°的圆心角所对的弧长是
,即.于是n°的圆心角所对的弧长为l=.
【知识归纳】
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
问题2:由扇形的定义可知,扇形面积就是圆面积的一部分,想一想,如何计算圆的面积
1°的圆心角所对的扇形面积是多少
n°的圆心角呢
解:在半径为R的圆中,因为360°的圆心角所对的扇形的面积就是圆面积
S=πR2
,所以圆心角是1°的扇形面积是
,于是圆心角为
n°的扇形
面积是S扇形
=.
【知识归纳】
1.
在半径为
R
的圆中,1°的圆心角所对的弧长是,n°的圆心角所对的弧长是
.
2.
在半径为
R
的圆中,1°的圆心角所对的扇形面积是
,n°的圆心角所对的扇形面积是.
3.
半径为
R,弧长为
l
的扇形面积
S扇形
=.
3.例题精讲
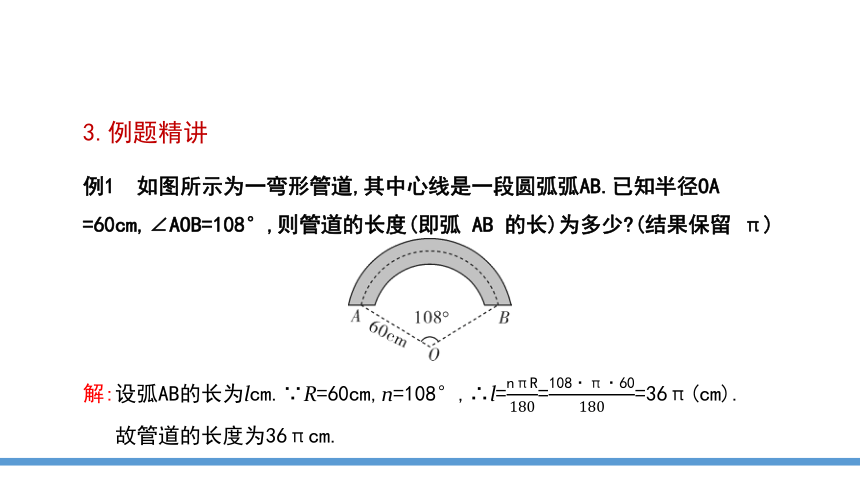
例1
如图所示为一弯形管道,其中心线是一段圆弧弧AB.已知半径OA
=60cm,∠AOB=108°,则管道的长度(即弧
AB
的长)为多少 (结果保留
π)
解:设弧AB的长为lcm.∵R=60cm,n=108°,∴l===36π(cm).
故管道的长度为36πcm.
例2
如图,两个同心圆被两条半径截得的弧
AB
的长度为5π, CD
的长度为
7π,AC
=
4,求阴影部分的面积(AB-
DC
的面积).
解:设圆心角为n°,则 CD
的长
l1=
,
AB
的长
l2
=.
∴
S阴影
=
-
=
(
-
)
=(+
)(-)
=(
+)
(-)
=(l1+l2
)(-)=(7π+5π)×4
=
24π.
故阴影部分的面积为
24π.
5.课堂小结
小结:1.
弧长公式.
2.
扇形的面积公式.
反思:
解决部分与整体之间关系的问题,往往要用到比例的方法;能从函数的观点去分析和理解弧长公式和扇形面积公式.
第
2
课时
圆锥的侧面积和全面积
一
学习目标
1.
通过实验,知道圆锥的侧面展开图是扇形,并了解圆锥各部分名称.
2.
能够计算圆锥的侧面积和全面积.
二
重难点
重点:了解圆锥的侧面积、全面积和计算公式,并能用它进行计算.
难点:探求圆锥的侧面积、全面积和计算公式的过程.
1.知识回顾
三
教学过程
(1)在半径为
R
的圆中,n°的圆心角所对的弧长是
.
(2)在半径为
R
的圆中,n°的圆心角所对的扇形面积是.
(3)半径为
R,弧长为
l
的扇形面积
S扇形
=.
2.探究新知
我们知道,圆锥是由一个底面和一个侧面围成的几何体,如图,我们把连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.连接顶点和底面圆心的线段叫做圆锥的高.
问题
圆锥的侧面展开图是什么图形 如何计算圆锥的侧面积 如何计算圆锥的全面积
解:设圆锥的母线长为l,底面圆的半径为r,
那么这个扇形的半径为l,扇形的弧长为2πr,因此圆锥的侧面积为πrl,圆锥的全面积为πr(r+l).
【知识归纳】
1.
圆锥的母线l,圆锥的高h,底面圆的半径r,存在关系式:l2=h2+r2
;
2.
圆锥的侧面积S=πrl;
3.
圆锥的全面积S全=S底+S侧=πr2+πrl
【分析】如图,沿一条母线将圆锥侧面剪开并展平,容易得到,圆锥的侧面展开图是一个扇形.
3.例题精讲
例
蒙古包可以近似地看作由圆锥和圆柱组成.如果想用毛毡搭建20个底面积为12m2
,高为3.2m.外围高1.8m的蒙古包,至少需要多少平方米的毛毡(π取
3.142,结果取整数)
解:如图是一个蒙古包的示意图
根据题意,
下部圆柱的底面积为12m2
,
高
h2=1.
8m;
上部圆锥的高
h1=3.
2-1.
8=1.
4(m).
圆柱的底面圆的半径
r
=
≈1.
954(m),
侧面积为
2π×1.
954×1.
8≈22.
10(m2
).
圆锥的母线长
l≈≈2.
404(m).
侧面展开扇形的弧长为×2.
404×12.
28≈14.
76
(m).
因此,搭建
20
个这样的蒙古包至少需要毛毡
20×
(22.
10+14.
76)≈738(m2
).
5.课堂小结
小结:1.
圆锥的母线长等于扇形的半径;扇形的弧长等于圆锥底面圆的周长.
2.圆锥侧面展开图的有关计算.
反思:
通过运用公式解决实际问题,让学生懂得数学与人
类生活的密切联系,激发学习兴趣.
感谢收看!
24.4
弧长和扇形面积
第1课时
弧长和扇形面积
一
学习目标
1.
以圆的周长和面积为基础,探究弧长和扇形的面积公式,并会用来计算弧长和扇形面积.
2.
能利用弧长、扇形面积计算公式计算简单组合图形的周长和面积.
二
重难点
重点:经历探究弧长和扇形面积公式的过程.能够推导公式.
难点:用公式解决实际问题.
1.情景导入
三
教学过程
中国是世界上最早使用扇子的国家.
自扇子传世以来,相关的趣闻轶事多不胜数;随着时代的发展,扇子不仅仅是一种纳凉工具,更是一种备受人们喜爱的工艺品.
如图,
扇子面的纸张面积如何计算,外围弧长又如何计算
2.探究新知
问题
1
我们知道弧是圆的一部分,弧长就是圆周长的一部分.想一想,如何计算圆周长 圆的周长可以看作是多少度的圆心角所对的弧长 由此发现,1°的圆心角所对的弧长是多少
n°的圆心角呢
解:在半径为R的圆中,因为360°的圆心角所对的弧长就是圆周长C=2πR,所以1°的圆心角所对的弧长是
,即.于是n°的圆心角所对的弧长为l=.
【知识归纳】
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.
问题2:由扇形的定义可知,扇形面积就是圆面积的一部分,想一想,如何计算圆的面积
1°的圆心角所对的扇形面积是多少
n°的圆心角呢
解:在半径为R的圆中,因为360°的圆心角所对的扇形的面积就是圆面积
S=πR2
,所以圆心角是1°的扇形面积是
,于是圆心角为
n°的扇形
面积是S扇形
=.
【知识归纳】
1.
在半径为
R
的圆中,1°的圆心角所对的弧长是,n°的圆心角所对的弧长是
.
2.
在半径为
R
的圆中,1°的圆心角所对的扇形面积是
,n°的圆心角所对的扇形面积是.
3.
半径为
R,弧长为
l
的扇形面积
S扇形
=.
3.例题精讲
例1
如图所示为一弯形管道,其中心线是一段圆弧弧AB.已知半径OA
=60cm,∠AOB=108°,则管道的长度(即弧
AB
的长)为多少 (结果保留
π)
解:设弧AB的长为lcm.∵R=60cm,n=108°,∴l===36π(cm).
故管道的长度为36πcm.
例2
如图,两个同心圆被两条半径截得的弧
AB
的长度为5π, CD
的长度为
7π,AC
=
4,求阴影部分的面积(AB-
DC
的面积).
解:设圆心角为n°,则 CD
的长
l1=
,
AB
的长
l2
=.
∴
S阴影
=
-
=
(
-
)
=(+
)(-)
=(
+)
(-)
=(l1+l2
)(-)=(7π+5π)×4
=
24π.
故阴影部分的面积为
24π.
5.课堂小结
小结:1.
弧长公式.
2.
扇形的面积公式.
反思:
解决部分与整体之间关系的问题,往往要用到比例的方法;能从函数的观点去分析和理解弧长公式和扇形面积公式.
第
2
课时
圆锥的侧面积和全面积
一
学习目标
1.
通过实验,知道圆锥的侧面展开图是扇形,并了解圆锥各部分名称.
2.
能够计算圆锥的侧面积和全面积.
二
重难点
重点:了解圆锥的侧面积、全面积和计算公式,并能用它进行计算.
难点:探求圆锥的侧面积、全面积和计算公式的过程.
1.知识回顾
三
教学过程
(1)在半径为
R
的圆中,n°的圆心角所对的弧长是
.
(2)在半径为
R
的圆中,n°的圆心角所对的扇形面积是.
(3)半径为
R,弧长为
l
的扇形面积
S扇形
=.
2.探究新知
我们知道,圆锥是由一个底面和一个侧面围成的几何体,如图,我们把连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.连接顶点和底面圆心的线段叫做圆锥的高.
问题
圆锥的侧面展开图是什么图形 如何计算圆锥的侧面积 如何计算圆锥的全面积
解:设圆锥的母线长为l,底面圆的半径为r,
那么这个扇形的半径为l,扇形的弧长为2πr,因此圆锥的侧面积为πrl,圆锥的全面积为πr(r+l).
【知识归纳】
1.
圆锥的母线l,圆锥的高h,底面圆的半径r,存在关系式:l2=h2+r2
;
2.
圆锥的侧面积S=πrl;
3.
圆锥的全面积S全=S底+S侧=πr2+πrl
【分析】如图,沿一条母线将圆锥侧面剪开并展平,容易得到,圆锥的侧面展开图是一个扇形.
3.例题精讲
例
蒙古包可以近似地看作由圆锥和圆柱组成.如果想用毛毡搭建20个底面积为12m2
,高为3.2m.外围高1.8m的蒙古包,至少需要多少平方米的毛毡(π取
3.142,结果取整数)
解:如图是一个蒙古包的示意图
根据题意,
下部圆柱的底面积为12m2
,
高
h2=1.
8m;
上部圆锥的高
h1=3.
2-1.
8=1.
4(m).
圆柱的底面圆的半径
r
=
≈1.
954(m),
侧面积为
2π×1.
954×1.
8≈22.
10(m2
).
圆锥的母线长
l≈≈2.
404(m).
侧面展开扇形的弧长为×2.
404×12.
28≈14.
76
(m).
因此,搭建
20
个这样的蒙古包至少需要毛毡
20×
(22.
10+14.
76)≈738(m2
).
5.课堂小结
小结:1.
圆锥的母线长等于扇形的半径;扇形的弧长等于圆锥底面圆的周长.
2.圆锥侧面展开图的有关计算.
反思:
通过运用公式解决实际问题,让学生懂得数学与人
类生活的密切联系,激发学习兴趣.
感谢收看!
同课章节目录
