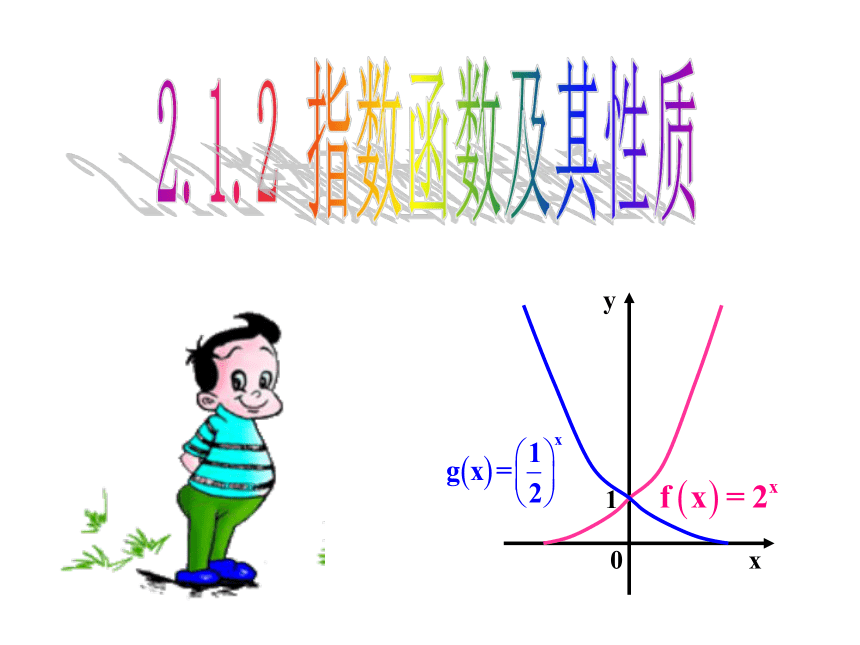
2.1.2指数函数及其性质

(共36张PPT)
1
0
x
y
一张白纸对折一次得两层，对折两次得4层，对折3次得8层，问若对折 x 次所得层数为y，则y与x 的函数表达式是？
可以准确写出来吗？
新课导入
问题1.
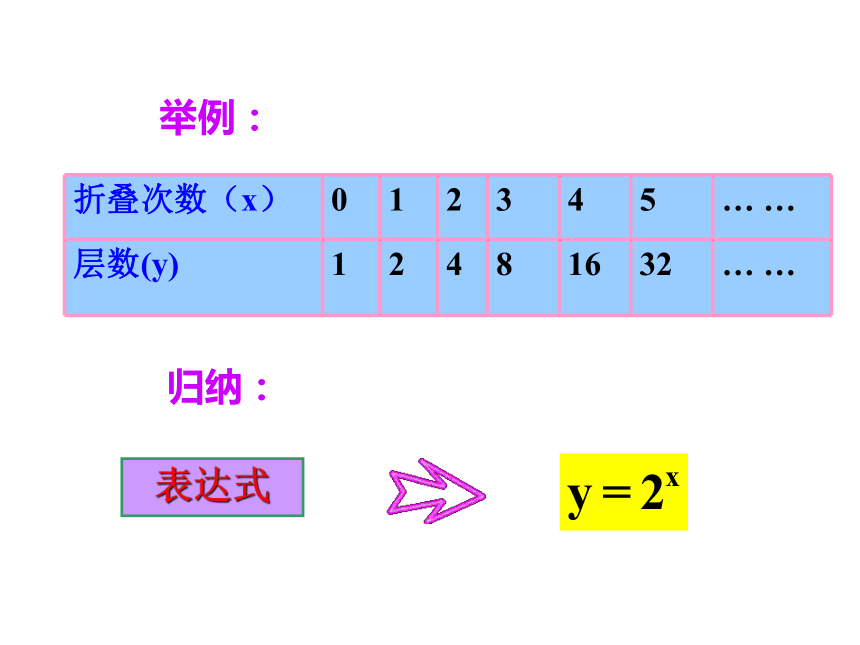
表达式
举例：
归纳：
折叠次数（x） 0 1 2 3 4 5 … …
层数(y) 1 2 4 8 16 32 … …
当生物死后,它机体内原有的碳-14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为‘‘半衰期”.根据此规律,人们获得了生物体内碳-14含量P 与死亡年数t之间的关系式：
问题2.
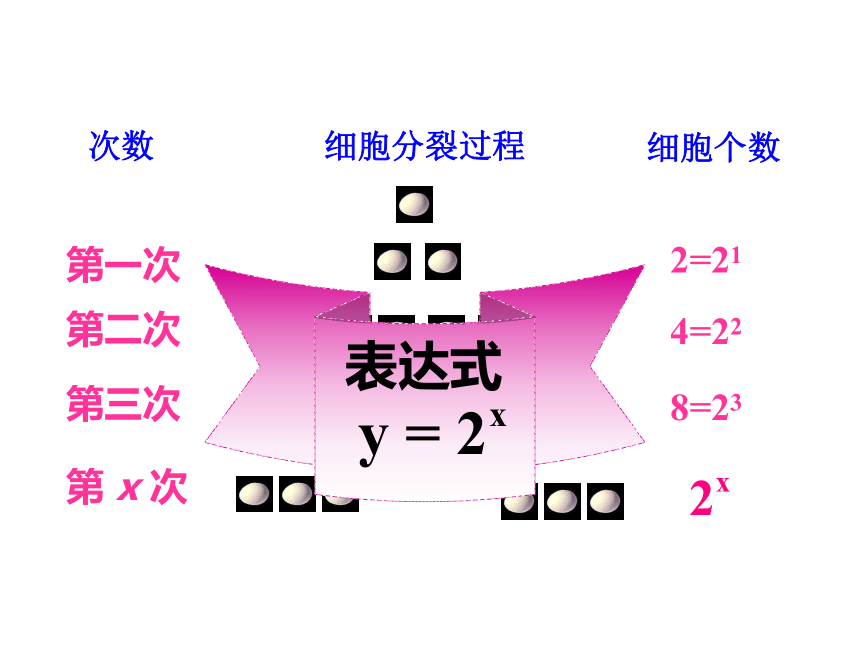
引例：某种细胞分裂时，由1个分裂成2个，2个分裂成4个，……. 1个这样的细胞分裂 x 次后，得到的细胞个数 y 与 x 的函数表达式是：
探究
次数
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
4=22
8=23
第 x 次
……
表达式
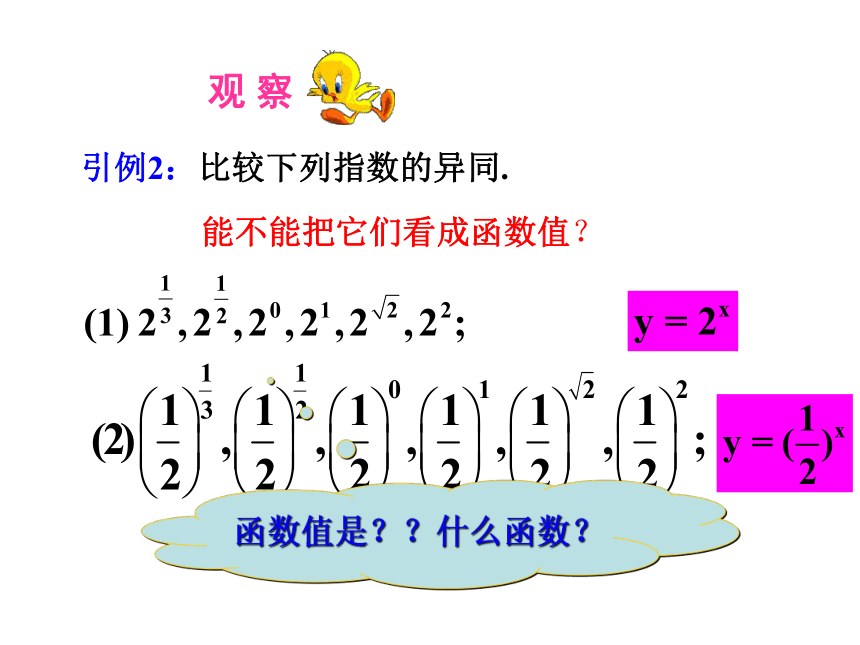
观 察
引例2：比较下列指数的异同.
能不能把它们看成函数值？
函数值是？？什么函数？
我们从以上两个引例中，抽象得到两个函数:
这两个函数有何特点
解析式 共同特征
探究
指数幂形式
自变量在指数位置
底数是常量
知识要点
指数函数定义：
形如y = ax ( a 0，且a 1)的函数叫做指数函数，其中x是自变量 .函数的定义域是R .
为何规定a 0，且a 1


0
1
a
思考
讨论：
当a<0时，a x有些会没有意义，如
当a=0时， a x有些会没有意义，如
当a=1时，a x 恒等于1，没有研究的必要.
a 0，且 a 1.
小练习
判断下例函数哪些是指数函数？
不是
是
不是
不是
不是
是
随着人民生活水平的提高，汽车的使用也越来越普遍，根据08年发改委发布的《未来我国汽车需求分析报告》判断，今后汽车需求量的年平均增长率预计可达到 7% .那么以后各年汽车需求量将是08年的多少倍？
即
解：由对应关系可知，函数关系式为
知识要点
指数函数图像：
（见下图）
用描点法作函数
动动手
1.列表
x … -3 -2 -1 0 1 2 3 …
y=2x … 1/8 1/4 1/2 1 2 4 8 …
y=3x … 1/27 1/9 1/3 1 3 9 27 …
2.描点
3.连线
x
y
1
2
3
-1
-2
-3
0
3
9
15
21
27
用描点法作函数
动动手
1.列表
x … -3 -2 -1 0 1 2 3 …
y=2-x … 8 4 2 1 1/2 1/4 1/8 …
y=3-x … 27 9 3 1 1/3 1/9 1/27 …
思考：若不用描点法，
这两个函数的图象又该
如何作出呢？
2.描点
3.连线
y=1
x
y
1
2
3
-1
-2
-3
0
1
3
5
7
9
27
观 察
这四个图像有何特点
y=ax（a>1）与 y=ax（0回答问题
问题一：图象分别在哪几个象限？
答：四个图象都在第＿＿＿＿象限
Ⅰ、Ⅱ
问题二：图象的上升、下降与底数a有联系吗？
答：当底数a＿＿时图象上升,底数a由大变小时函数图像＿＿＿＿（变化趋势）;当底数a______时图象下降．底数a由大变小时函数图像＿＿＿＿（变化趋势）
>1
1>a>0
平坦
陡峭
问题三：图象有哪些特殊的点？
答：四个图象都经过点＿＿＿＿．
（0，1）
问题四：图象定义域和值域范围？
答：定义域为＿＿．值域为＿＿＿＿．
R
(0, +∞)
知识要点
指数函数性质：
（见下表）
a>1
0图 象
(0,1)
y=1
y
x
y=ax
(a>1)
x
y
y=ax
(0性 质
定 义 域 :
R
值 域 :
( 0 , + ∞ )
必过 点：
( 0 , 1 )
x>0,y>1;
x<0, 0在 R 上是
增函数
x<0,y>1;
x>0,0在 R 上是
减函数
小练习
求下列函数的定义域：
解:
①
③
②
①
②
③
比较下列两组数的大小：
解:
探究总结
比较指数大小——常用方法，如下
① 构造函数法：要点是利用指数函数的单调性.数的特征是同底不同指（包括可以化为同底的），若底数是参变量需要注意分类讨论.
② 搭桥比较法：用别的数如0或1做桥.数的特征是不同底不同指.
课堂小结
1、指数函数概念
函数y = ax(a 0，且a 1)叫做指数函数，其中x是自变量 .
函数的定义域是R .
◆方法指导:
研究指数函数时，将a分为a>1和02、指数函数图像
（a>1）
(0,1)
y=1
y=ax
(a>1)
（0y=ax
(0(0,1)
y=1
y
x
y
x
3、指数函数性质
◆方法指导
利用函数图像研究函数性质是一种直观而形象的方法，记忆指数函数性质时可以联想它的图像.
（1）定义域： 值 域：
（2）函数的特殊值：
（3）函数的单调性：
随堂练习
1.求下列函数的定义域：
解:
2.比较下列各组数的大小：
解:
3.求满足条件的值：
解:
讨论：
解:
（1）当a<0时，没有意义.
（2）当a=1时，x=-1/5时, y1≡y2.
（3）当0-1/5时，y1y2.
（4）当a>1时，y=ax在R增函数； x=-1/5时, y1=y2; x>-1/5时，y1>y2; x<-1/5时，y1上题中，若把 2/3 改为a可不可以？怎么做？