2.2.1对数与对数运算
图片预览
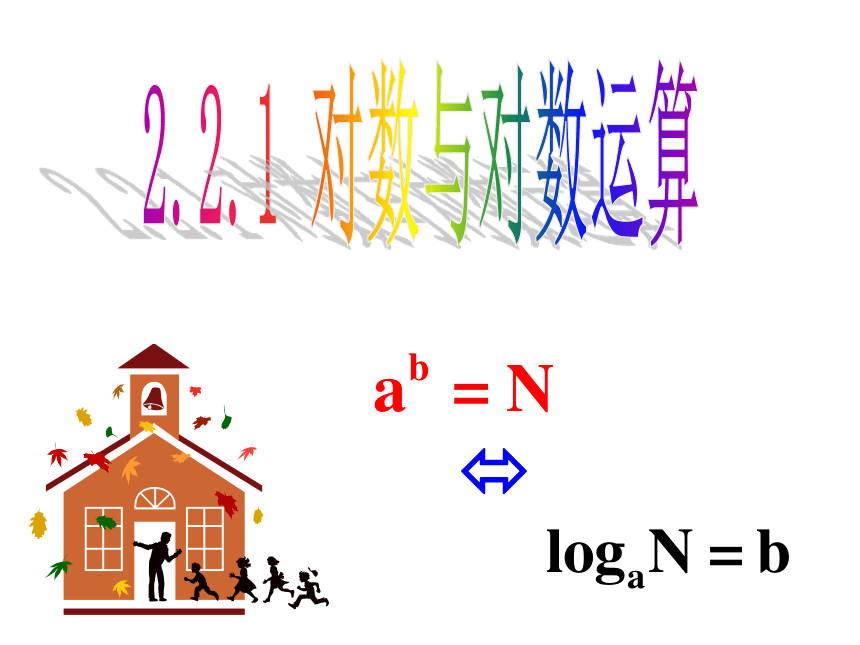


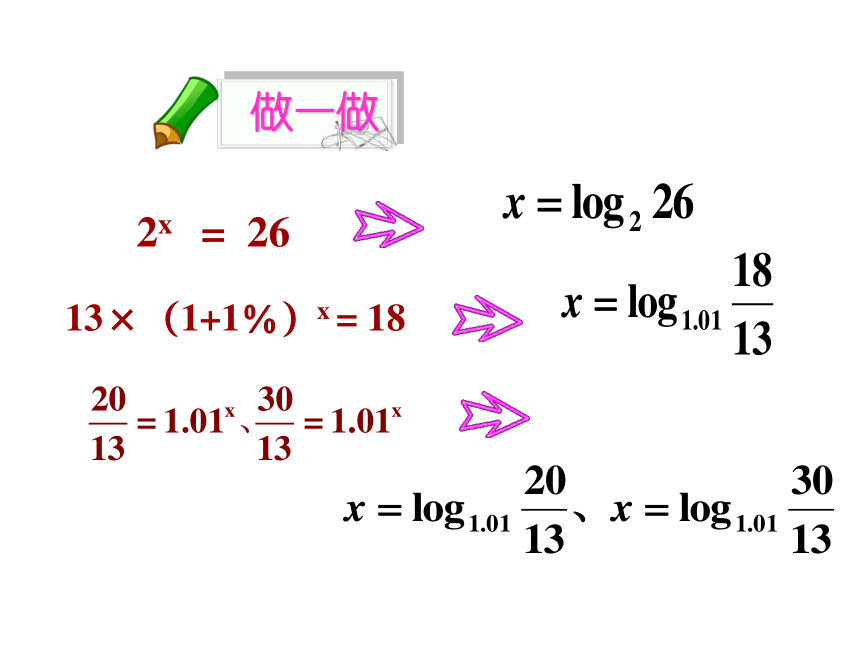



文档简介
(共38张PPT)
新课导入
回顾旧知
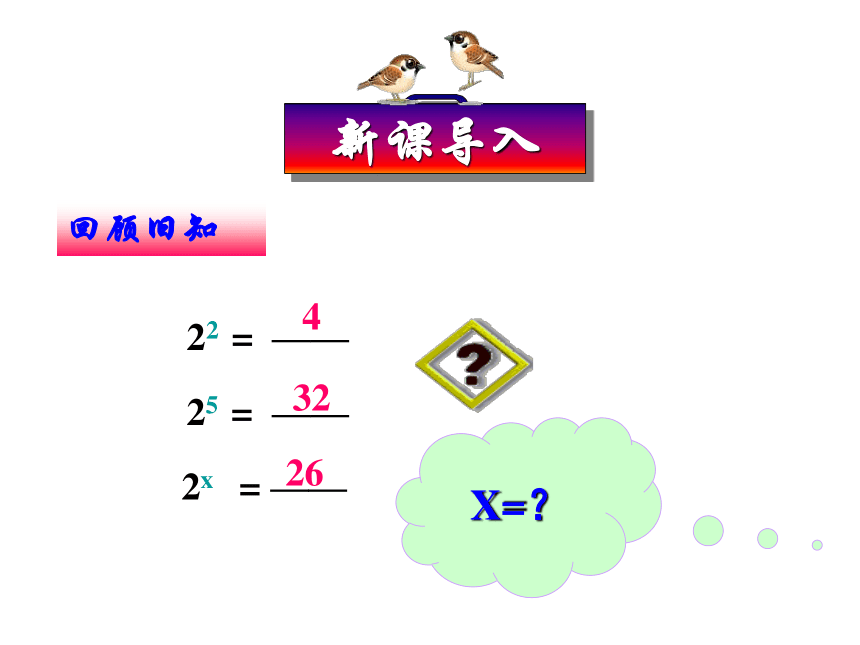
22 = ——
25 = ——
4
32
2x = ——
X=?
26
截止到1999年底,我国人口约13亿.如果今后能将人口年平均增长率控制在1%,那么经过20年后,我国人口数最多为多少(精确到亿)?到哪一年我国的人口数将达到18亿?
13×(1+1%)20 = 15.8625
13×(1+1%)x = 18
X=
能否用一个式子把表示出来吗
动动脑
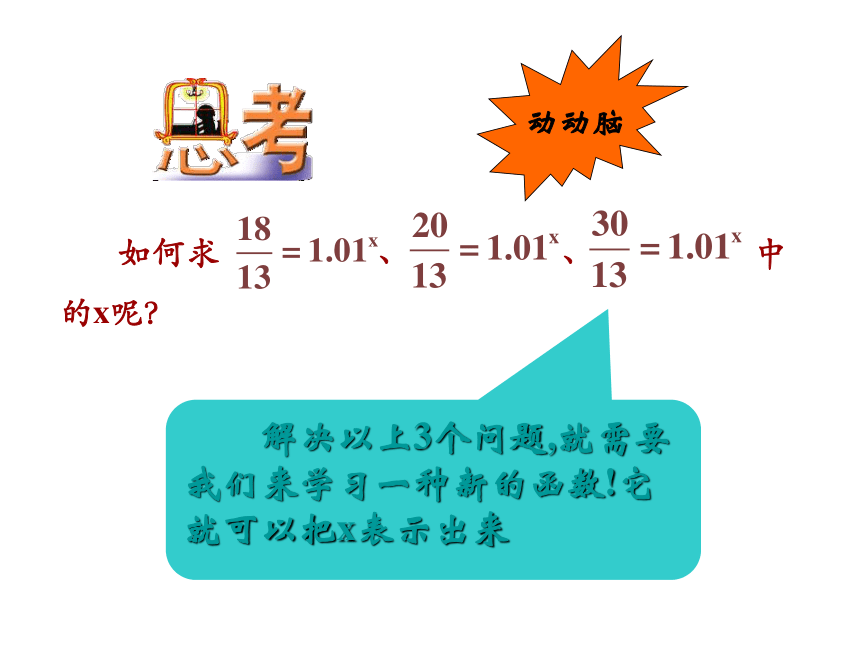
如何求 、 、 中的x呢?
解决以上3个问题,就需要我们来学习一种新的函数!它就可以把x表示出来
研讨
2x = 26
13×(1+1%)x = 18
以上3式都是已知底数和幂的值,求指数的问题.即指数式 ax = N 中,已知a 和N.求x的问题.(这里a>0且a≠0)
知识要点
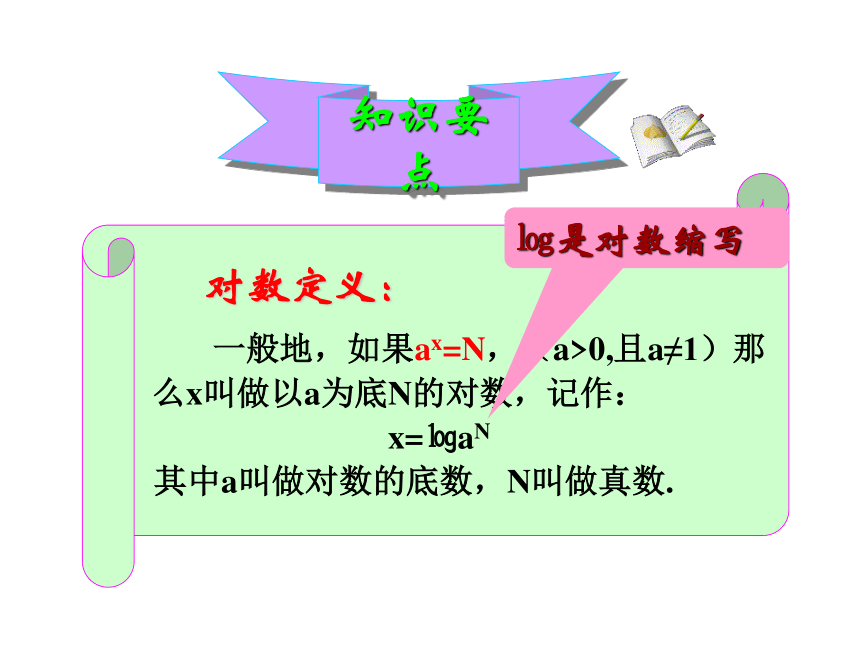
对数定义:
一般地,如果ax=N,(a>0,且a≠1)那么x叫做以a为底N的对数,记作:
x=㏒aN
其中a叫做对数的底数,N叫做真数.
㏒是对数缩写
做一做
2x = 26
13×(1+1%)x = 18
知识要点
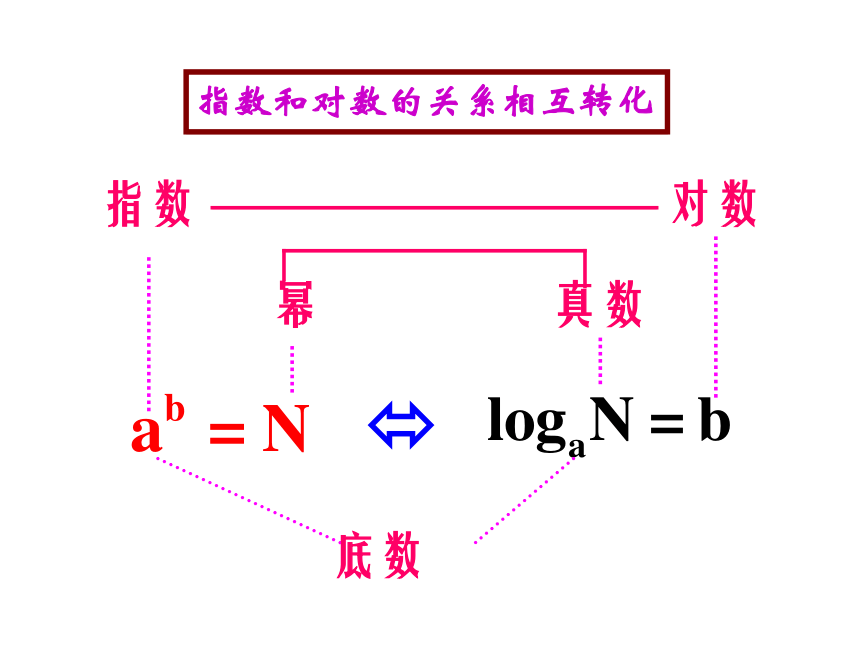
对数与指数间关系:
ax=N x=㏒aN.
(a>0,且a≠1)
底数
幂
真数
指数
对数
指数和对数的关系相互转化
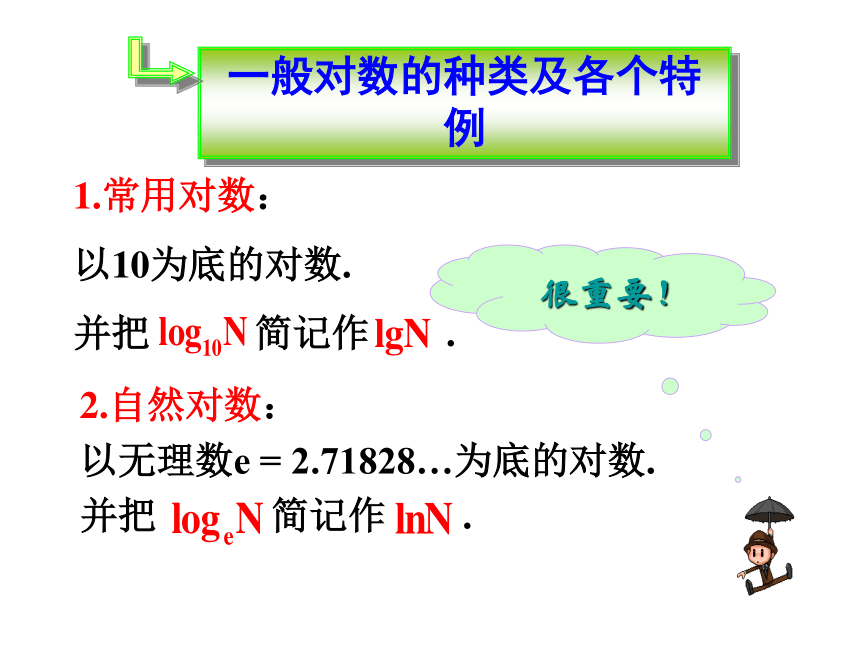
1.常用对数:
以10为底的对数.
并把 简记作 .
2.自然对数:
以无理数e = 2.71828…为底的对数.
并把 简记作 .
一般对数的种类及各个特例
很重要!
小练习
将下列指数式写成对数式:
(1) 32 = 9
(3) 2m = 3.15
(2) 3-4 = 1/81
解:
将下列对数式写成指数式:
解:
指数中的特殊结论:
能不能延伸到对数中来呢?
思考…
探究新知
结论
1.ax >0恒成立(a>0,且a≠1)
负数和零没有对数
2.a0 = 1(a>0,且a≠1)
loga1 = 0
3.a1 = a(a>0,且a≠1)
logaa = 1
4.令ax = N(a>0,且a≠1)
x=logaN
所以:
小练习
求下列各式的值:
解:
求对数
指数运算性质:
能不能延伸到对数中来呢?
思考…
探究
假设可以运用对数运算中:
证明:
同理
利用指数运算性质可以推导出对数的其它运算性质.
求证:
知识要点
对数运算性质:
推 导
推导:
由对数的定义可以得:
∴
即证得
证明: 设
性质(2)请自行推导得出.
小练习
求下列各式的值:
解:
研究
指数与对数对比表
式 子 ab =N logaN =b
名 称 a——幂的底数
b——幂的指数
N——幂值 a——对数的底数
b——a为底N的对数
N——真数
运算性质 am×an =am+n
am÷an =am-n
(am)n =amn logaMN =logaM+logaN
loga(M/N)=logaM-logaN
logaMP=plogaM
探 究
推导:
证明:
知识要点
换底公式:
小练习
在前面求我国人口多少年后达到18亿,列出式子如下:
一般的对数运算性质解不出.
利用换底公式与对数运算性质,
解:
课堂小结
1、对数的定义
如果ax=N,(a>0,且a≠1)那么x叫做以a为底N的对数,记作:
x=㏒aN
其中a叫做对数的底数,N叫做真数.
2、对数式与指数式的互换
ax=N x=㏒aN.
(a>0,且a≠1)
3、由对数定义得出的几个常用式子
(1)负数和零没有对数
(2)loga1 = 0
(3)logaa = 1
4、对数的运算性质
5、换底公式
很重要!
随堂练习
1.将下列对数式写成指数式,指数写成对数式:
解:
2.求下列各式的值:
解:
3.计算:
= 3
解:
换底公式的应用!
解:
还有其它方法?
思考
方法二:
解:
新课导入
回顾旧知
22 = ——
25 = ——
4
32
2x = ——
X=?
26
截止到1999年底,我国人口约13亿.如果今后能将人口年平均增长率控制在1%,那么经过20年后,我国人口数最多为多少(精确到亿)?到哪一年我国的人口数将达到18亿?
13×(1+1%)20 = 15.8625
13×(1+1%)x = 18
X=
能否用一个式子把表示出来吗
动动脑
如何求 、 、 中的x呢?
解决以上3个问题,就需要我们来学习一种新的函数!它就可以把x表示出来
研讨
2x = 26
13×(1+1%)x = 18
以上3式都是已知底数和幂的值,求指数的问题.即指数式 ax = N 中,已知a 和N.求x的问题.(这里a>0且a≠0)
知识要点
对数定义:
一般地,如果ax=N,(a>0,且a≠1)那么x叫做以a为底N的对数,记作:
x=㏒aN
其中a叫做对数的底数,N叫做真数.
㏒是对数缩写
做一做
2x = 26
13×(1+1%)x = 18
知识要点
对数与指数间关系:
ax=N x=㏒aN.
(a>0,且a≠1)
底数
幂
真数
指数
对数
指数和对数的关系相互转化
1.常用对数:
以10为底的对数.
并把 简记作 .
2.自然对数:
以无理数e = 2.71828…为底的对数.
并把 简记作 .
一般对数的种类及各个特例
很重要!
小练习
将下列指数式写成对数式:
(1) 32 = 9
(3) 2m = 3.15
(2) 3-4 = 1/81
解:
将下列对数式写成指数式:
解:
指数中的特殊结论:
能不能延伸到对数中来呢?
思考…
探究新知
结论
1.ax >0恒成立(a>0,且a≠1)
负数和零没有对数
2.a0 = 1(a>0,且a≠1)
loga1 = 0
3.a1 = a(a>0,且a≠1)
logaa = 1
4.令ax = N(a>0,且a≠1)
x=logaN
所以:
小练习
求下列各式的值:
解:
求对数
指数运算性质:
能不能延伸到对数中来呢?
思考…
探究
假设可以运用对数运算中:
证明:
同理
利用指数运算性质可以推导出对数的其它运算性质.
求证:
知识要点
对数运算性质:
推 导
推导:
由对数的定义可以得:
∴
即证得
证明: 设
性质(2)请自行推导得出.
小练习
求下列各式的值:
解:
研究
指数与对数对比表
式 子 ab =N logaN =b
名 称 a——幂的底数
b——幂的指数
N——幂值 a——对数的底数
b——a为底N的对数
N——真数
运算性质 am×an =am+n
am÷an =am-n
(am)n =amn logaMN =logaM+logaN
loga(M/N)=logaM-logaN
logaMP=plogaM
探 究
推导:
证明:
知识要点
换底公式:
小练习
在前面求我国人口多少年后达到18亿,列出式子如下:
一般的对数运算性质解不出.
利用换底公式与对数运算性质,
解:
课堂小结
1、对数的定义
如果ax=N,(a>0,且a≠1)那么x叫做以a为底N的对数,记作:
x=㏒aN
其中a叫做对数的底数,N叫做真数.
2、对数式与指数式的互换
ax=N x=㏒aN.
(a>0,且a≠1)
3、由对数定义得出的几个常用式子
(1)负数和零没有对数
(2)loga1 = 0
(3)logaa = 1
4、对数的运算性质
5、换底公式
很重要!
随堂练习
1.将下列对数式写成指数式,指数写成对数式:
解:
2.求下列各式的值:
解:
3.计算:
= 3
解:
换底公式的应用!
解:
还有其它方法?
思考
方法二:
解:
